来源：《斯坦福数据挖掘教程·第三版》对应的公开英文书和PPT

Chapter 5 Link Analysis

Terms: words or other strings of characters other than white space.

An inverted index is a data structure that makes it easy, given a term, to find (pointers to) all the places where that term occurs.

Techniques for fooling search engines into believing your page is about something it is not, are called term spam. The ability of term spammers to operate so easily rendered early search engines almost useless. To combat term spam, Google introduced two innovations:

1. PageRank was used to simulate where Web surfers, starting at a random page, would tend to congregate if they followed randomly chosen out-links from the page at which they were currently located, and this process were allowed to iterate many times. Pages that would have a large number of surfers were considered more “important” than pages that would rarely be visited. Google prefers important pages to unimportant pages when deciding which pages to show first in response to a search query.
2. The content of a page was judged not only by the terms appearing on that page, but by the terms used in or near the links to that page. Note that while it is easy for a spammer to add false terms to a page they control, they cannot as easily get false terms added to the pages that link to their own page, if they do not control those pages.

Suppose we start a random surfer at any of the n pages of the Web with equal probability. Then the initial vector $v_0$ will have 1/n for each component. If M is the transition matrix of the Web, then after one step, the distribution of the surfer will be $M{v}_0$, after two steps it will be $M(M{v}_0)=M^2{v}_0$, and so on. In general, multiplying the initial vector $v_0$ by M a total of i times will give us the distribution of the surfer after i steps.

This sort of behavior is an example of the ancient theory of Markov processes. It is known that the distribution of the surfer approaches a limiting distribution v that satisfies $v=Mv$, provided two conditions are met:

1. The graph is strongly connected; that is, it is possible to get from any node to any other node.
2. There are no dead ends: nodes that have no arcs out.

An early study of the Web found it to have the structure shown in Fig. 5.2. There was a large strongly connected component (SCC), but there were several other portions that were almost as large.

1. The in-component, consisting of pages that could reach the SCC by following links, but were not reachable from the SCC.
2. The out-component, consisting of pages reachable from the SCC but unable to reach the SCC.
3. Tendrils, which are of two types. Some tendrils consist of pages reachable from the in-component but not able to reach the in-component. The other tendrils can reach the out-component, but are not reachable from the out-component.

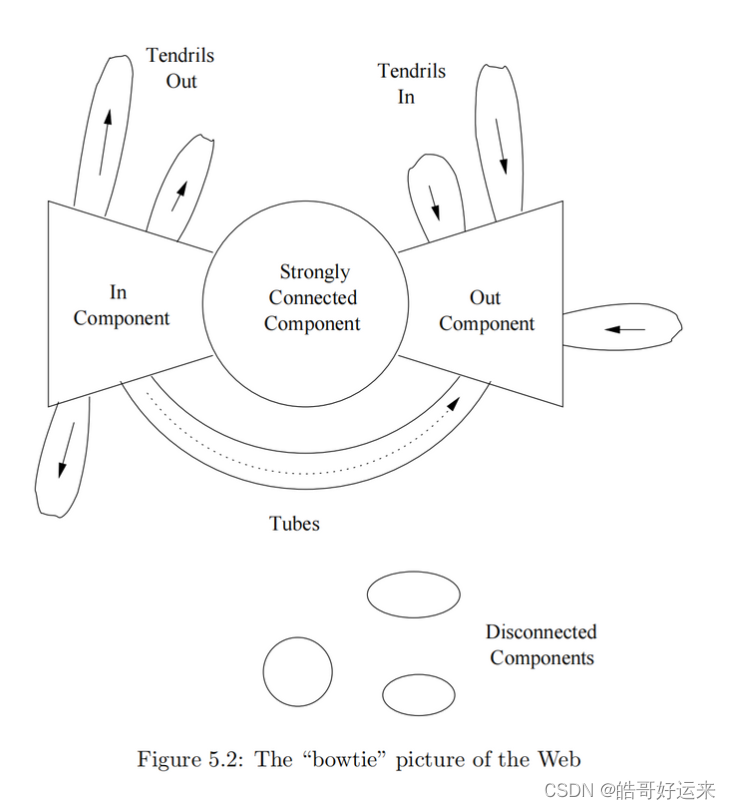
Tubes, which are pages reachable from the in-component and able to reach the out-component, but unable to reach the SCC or be reached from the SCC.
Isolated components that are unreachable from the large components (the SCC, in- and out-components) and unable to reach those components.

There are really two problems we need to avoid. First is the dead end, a page that has no links out. Surfers reaching such a page disappear, and the result is that in the limit no page that can reach a dead end can have any PageRank at all.
The second problem is groups of pages that all have out-links but they never link to any other pages. These structures are called spider traps. Both these problems are solved by a method called “taxation,” where we assume a random surfer has a finite probability of leaving the Web at any step, and new surfers are started at each page. We shall illustrate this process as we study each of the two problem cases.

A matrix whose column sums are at most 1 is called substochastic. If we compute $M^{i}v$ for increasing powers of a substochastic matrix M, then some or all of the components of the vector go to 0. That is, importance “drains out” of the Web, and we get no information about the relative importance of pages.

There are two approaches to dealing with dead ends.

1. We can drop the dead ends from the graph, and also drop their incoming arcs. Doing so may create more dead ends, which also have to be dropped, recursively. However, eventually we wind up with a strongly-connected component, none of whose nodes are dead ends. In terms of Fig. 5.2, recursive deletion of dead ends will remove parts of the out-component, tendrils, and tubes, but leave the SCC and the in-component, as well as parts of any small isolated components.4
2. We can modify the process by which random surfers are assumed to move about the Web. This method, which we refer to as “taxation,” also solves the problem of spider traps.

If we use the first approach, recursive deletion of dead ends, then we solve the remaining graph G by whatever means are appropriate, including the taxation method if there might be spider traps in G. Then, we restore the graph, but keep the PageRank values for the nodes of G. Nodes not in G, but with predecessors all in G can have their PageRank computed by summing, over all predecessors p, the PageRank of p divided by the number of successors of p in the full graph. Now there may be other nodes, not in G, that have the PageRank of all their predecessors computed. These may have their own PageRank computed by the same process. Eventually, all nodes outside G will have their PageRank computed; they can surely be computed in the order opposite to that in which they were deleted.

Since C was last to be deleted, we know all its predecessors have PageRank computed. These predecessors are A and D. In Fig. 5.4, A has three successors, so it contributes 1/3 of its PageRank to C. Page D has two successors in Fig. 5.4, so it contributes half its PageRank to C. Thus, the PageRank of C is $\frac{1}{3}\times \frac{2}{9}+\frac{1}{2}\times \frac{3}{9}=\frac{13}{54}$.

To avoid the problem illustrated by Example 5.5, we modify the calculation of PageRank by allowing each random surfer a small probability of teleporting to a random page, rather than following an out-link from their current page. The iterative step, where we compute a new vector estimate of PageRank $v^{\prime }$ from the current PageRank estimate v and the transition matrix M is:

$$v^{\prime }=\beta Mv+(1-\beta )e/n$$

where $\beta$ is a chosen constant, usually in the range 0.8 to 0.9, e is a vector of all 1’s with the appropriate number of components, and n is the number of nodes in the Web graph. The term $\beta Mv$ represents the case where, with probability $\beta$, the random surfer decides to follow an out-link from their present page. The term $(1-\beta )e/n$ is a vector each of whose components has value $(1-\beta )/n$ and represents the introduction, with probability $1-\beta$, of a new random surfer at a random page.

The mathematical formulation for the iteration that yields topic-sensitive PageRank is similar to the equation we used for general PageRank. The only difference is how we add the new surfers. Suppose S is a set of integers consisting of the row/column numbers for the pages we have identified as belonging to a certain topic (called the teleport set). Let $e_S$ be a vector that has 1 in the components in S and 0 in other components. Then the topic-sensitive PageRank for S is the limit of the iteration

$$v^{\prime }=\beta Mv+(1-\beta )e_S/|S|$$

Here, as usual, M is the transition matrix of the Web, and |S| is the size of set S.

In order to integrate topic-sensitive PageRank into a search engine, we must:

1. Decide on the topics for which we shall create specialized PageRank vectors.
2. Pick a teleport set for each of these topics, and use that set to compute the topic-sensitive PageRank vector for that topic.
3. Find a way of determining the topic or set of topics that are most relevant for a particular search query.
4. Use the PageRank vectors for that topic or topics in the ordering of the responses to the search query.

The third step is probably the trickiest, and several methods have been proposed. Some possibilities:
(a) Allow the user to select a topic from a menu.
(b) Infer the topic(s) by the words that appear in the Web pages recently searched by the user, or recent queries issued by the user.
© Infer the topic(s) by information about the user, e.g., their bookmarks or their stated interests on Facebook.

Once we have identified a large collection of words that appear much more frequently in the sports sample than in the background, and we do the same for all the topics on our list, we can examine other pages and classify them by topic. Here is a simple approach. Suppose that $S_1,S_2,...,S_k$ are the sets of words that have been determined to be characteristic of each of the topics on our list. Let P be the set of words that appear in a given page P. Compute
the Jaccard similarity between P and each of the $S_i$’s. Classify the page as that topic with the highest Jaccard similarity. Note that all Jaccard similarities may be very low, especially if the sizes of the sets $S_i$ are small. Thus, it is important to pick reasonably large sets $S_i$ to make sure that we cover all aspects of the topic represented by the set.

The techniques for artificially increasing the PageRank of a page are collectively called link spam.

A collection of pages whose purpose is to increase the PageRank of a certain page or pages is called a spam farm. Figure 5.16 shows the simplest form of spam farm. From the point of view of the spammer, the Web is divided into three parts:

1. Inaccessible pages: the pages that the spammer cannot affect. Most of the Web is in this part.
2. Accessible pages: those pages that, while they are not controlled by the spammer, can be affected by the spammer.
3. Own pages: the pages that the spammer owns and controls.
   

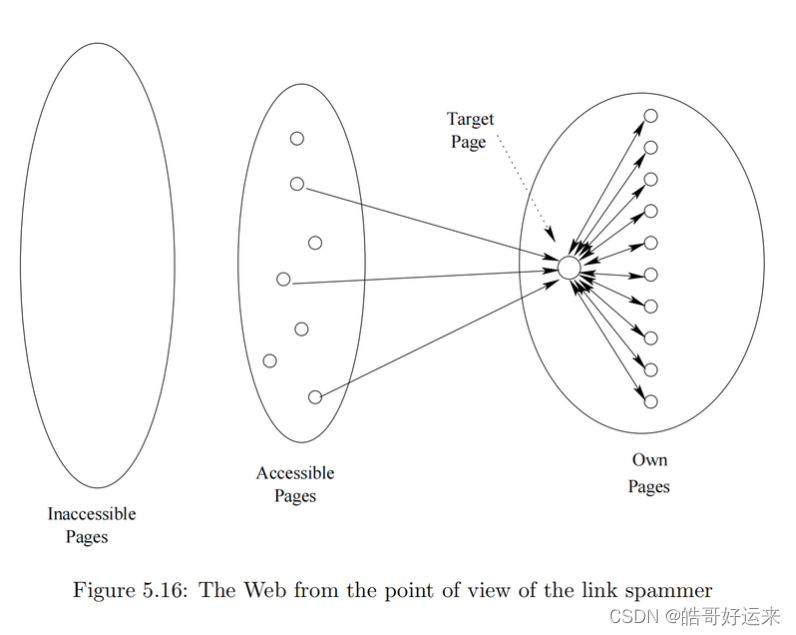
In the spam farm, there is one page t, the target page, at which the spammer attempts to place as much PageRank as possible. There are a large number m of supporting pages, that accumulate the portion of the PageRank that is distributed equally to all pages (the fraction $1-\beta$ of the PageRank that represents surfers going to a random page). The supporting pages also prevent the PageRank of t from being lost, to the extent possible, since some will be taxed away at each round. Notice that t has a link to every supporting page, and every supporting page links only to t.

Analysis of a Spam Farm

Suppose that PageRank is computed using a taxation parameter $\beta$, typically around 0.85. That is, $\beta$ is the fraction of a page’s PageRank that gets distributed to its successors at the next round. Let there be $n$ pages on the Web in total, and let some of them be a spam farm of the form suggested in Fig. 5.16, with a target page $t$ and m supporting pages. Let $x$ be the amount of PageRank contributed by the accessible pages. That is, $x$ is the sum, over all accessible pages $p$ with a link to $t$, of the PageRank of $p$ times $\beta$, divided by the number of successors of $p$. Finally, let $y$ be the unknown PageRank of $t$. We shall solve for $y$.

First, the PageRank of each supporting page is:

$$\beta y/m+(1-\beta )/n$$

The first term represents the contribution from $t$. The PageRank $y$ of $t$ is taxed, so only $\beta y$ is distributed to t’s successors. That PageRank is divided equally among the m supporting pages. The second term is the supporting page’s share of the fraction $1-\beta$ of the PageRank that is divided equally among all pages on the Web. Now, let us compute the PageRank y of target page $t$. Its PageRank comes from three sources:

1. Contribution x from outside, as we have assumed.
2. $\beta$ times the PageRank of every supporting page; that is,$\beta (\beta y/m+(1-\beta )/n)$.
3. $(1-\beta )/n$, the share of the fraction $1-\beta$ of the PageRank that belongs to t. This amount is negligible and will be dropped to simplify the analysis.

Thus,

$$y=\frac{x}{1-{\beta }^2}+c\frac{m}{n}$$

where $c=\beta (1-\beta )/(1-{\beta }^2)=\beta /(1+\beta ).$

TrustRank is topic-sensitive PageRank, where the “topic” is a set of pages believed to be trustworthy (not spam). The theory is that while a spam page might easily be made to link to a trustworthy page, it is unlikely that a trustworthy page would link to a spam page.

To implement TrustRank, we need to develop a suitable teleport set of trustworthy pages. Two approaches that have been tried are:

1. Let humans examine a set of pages and decide which of them are trustworthy. For example, we might pick the pages of highest PageRank to examine, on the theory that, while link spam can raise a page’s rank from the bottom to the middle of the pack, it is essentially impossible to give a spam page a PageRank near the top of the list.
2. Pick a domain whose membership is controlled, on the assumption that it is hard for a spammer to get their pages into these domains. For example, we could pick the .edu domain, since university pages are unlikely to be spam farms. We could likewise pick .mil, or .gov. However, the problem with these specific choices is that they are almost exclusively US sites. To get a good distribution of trustworthy Web pages, we should include the
   analogous sites from foreign countries, e.g., ac.il, or edu.sg.

The idea behind spam mass is that we measure for each page the fraction of its PageRank that comes from spam. We do so by computing both the ordinary PageRank and the TrustRank based on some teleport set of trustworthy pages. Suppose page p has PageRank r and TrustRank t. Then the spam mass of p is $(r-t)/r$. A negative or small positive spam mass means that p is probably not a spam page, while a spam mass close to 1 suggests that the page probably is spam. It is possible to eliminate pages with a high spam mass from the index of Web pages used by a search engine, thus eliminating a great deal of the link spam without having to identify particular structures that spam farmers use.

While PageRank assumes a one-dimensional notion of importance for pages, HITS views important pages as having two flavors of importance.

1. Certain pages are valuable because they provide information about a topic. These pages are called authorities.
2. Other pages are valuable not because they provide information about any topic, but because they tell you where to go to find out about that topic. These pages are called hubs.

To formalize the above intuition, we shall assign two scores to each Web page. One score represents the hubbiness of a page – that is, the degree to which it is a good hub, and the second score represents the degree to which the page is a good authority. Assuming that pages are enumerated, we represent these scores by vectors h and a. The ith component of h gives the hubbiness of the ith page, and the ith component of a gives the authority of the same page.
While importance is divided among the successors of a page, as expressed by the transition matrix of the Web, the normal way to describe the computation of hubbiness and authority is to add the authority of successors to estimate hubbiness and to add hubbiness of predecessors to estimate authority. If that is all we did, then the hubbiness and authority values would typically grow beyond bounds. Thus, we normally scale the values of the vectors h and a so
that the largest component is 1. An alternative is to scale so that the sum of components is 1.
To describe the iterative computation of h and a formally, we use the link matrix of the Web, L. If we have n pages, then L is an $n\times n$ matrix, and $L_{ij}=1$ if there is a link from page i to page j, and $L_{ij}=0$ if not. We shall also have need for $L^T$, the transpose of L. That is, $L_{ij}^T=1$ if there is a link from page j to page i, and $L_{ij}^T=0$ otherwise. Notice that $L^T$ is similar to the matrix M that we used for PageRank, but where $L^T$ has 1, M has a fraction —— 1 divided by the number of out-links from the page represented by that column.

The fact that the hubbiness of a page is proportional to the sum of the authority of its successors is expressed by the equation $h=\lambda La$, where λ is an unknown constant representing the scaling factor needed. Likewise, the fact that the authority of a page is proportional to the sum of the hubbinesses of its predecessors is expressed by $a=\mu L^{T}h$, where µ is another scaling constant. These equations allow us to compute the hubbiness and authority independently, by substituting one equation in the other, as:

$$h=\lambda \mu L{L}^{T}h$$

$$a=\lambda \mu L^{T}La$$

However, since $L{L}^T$ and $L^{T}L$ are not as sparse as $L$ and $L^T$, we are usually better off computing h and a in a true mutual recursion. That is, start with h a vector of all 1’s.

1. Compute $a=L^{T}h$ and then scale so the largest component is 1.
2. Next, compute $h=La$ and scale again.

Summary of Chapter 5

• Term Spam: Early search engines were unable to deliver relevant results because they were vulnerable to term spam – the introduction into Web pages of words that misrepresented what the page was about.
• The Google Solution to Term Spam: Google was able to counteract term spam by two techniques. First was the PageRank algorithm for determining the relative importance of pages on the Web. The second was a strategy of believing what other pages said about a given page, in or near their links to that page, rather than believing only what the page said about itself.
• PageRank: PageRank is an algorithm that assigns a real number, called its PageRank, to each page on the Web. The PageRank of a page is a measure of how important the page is, or how likely it is to be a good response to a search query. In its simplest form, PageRank is a solution to the recursive equation “a page is important if important pages link to it.”
• Transition Matrix of the Web: We represent links in the Web by a matrix whose ith row and ith column represent the ith page of the Web. If there are one or more links from page j to page i, then the entry in row i and column j is 1/k, where k is the number of pages to which page j links. Other entries of the transition matrix are 0.
• Computing PageRank on Strongly Connected Web Graphs: For strongly connected Web graphs (those where any node can reach any other node), PageRank is the principal eigenvector of the transition matrix. We can compute PageRank by starting with any nonzero vector and repeatedly multiplying the current vector by the transition matrix, to get a better estimate. After about 50 iterations, the estimate will be very close to the limit, which is the true PageRank.
• The Random Surfer Model: Calculation of PageRank can be thought of as simulating the behavior of many random surfers, who each start at a random page and at any step move, at random, to one of the pages to which their current page links. The limiting probability of a surfer being at a given page is the PageRank of that page. The intuition is that people tend to create links to the pages they think are useful, so random surfers will tend to be at a useful page.
• Dead Ends: A dead end is a Web page with no links out. The presence of dead ends will cause the PageRank of some or all of the pages to go to 0 in the iterative computation, including pages that are not dead ends. We can eliminate all dead ends before undertaking a PageRank calculation by recursively dropping nodes with no arcs out. Note that dropping one node can cause another, which linked only to it, to become a dead end, so the process must be recursive.
• Spider Traps: A spider trap is a set of nodes that, while they may link to each other, have no links out to other nodes. In an iterative calculation of PageRank, the presence of spider traps cause all the PageRank to be captured within that set of nodes.
• Taxation Schemes: To counter the effect of spider traps (and of dead ends, if we do not eliminate them), PageRank is normally computed in a way that modifies the simple iterative multiplication by the transition matrix. A parameter $\beta$ is chosen, typically around 0.85. Given an estimate of the PageRank, the next estimate is computed by multiplying the estimate by $\beta$ times the transition matrix, and then adding $(1-\beta )/n$ to the estimate for each page, where n is the total number of pages.
• Taxation and Random Surfers: The calculation of PageRank using taxation parameter $\beta$ can be thought of as giving each random surfer a probability $1-\beta$ of leaving the Web, and introducing an equivalent number of surfers randomly throughout the Web.
• Efficient Representation of Transition Matrices: Since a transition matrix is very sparse (almost all entries are 0), it saves both time and space to represent it by listing its nonzero entries. However, in addition to being sparse, the nonzero entries have a special property: they are all the same in any given column; the value of each nonzero entry is the inverse of the number of nonzero entries in that column. Thus, the preferred
  representation is column-by-column, where the representation of a column is the number of nonzero entries, followed by a list of the rows where those entries occur.
• Very Large-Scale Matrix–Vector Multiplication: For Web-sized graphs, it may not be feasible to store the entire PageRank estimate vector in the main memory of one machine. Thus, we can break the vector into k segments and break the transition matrix into $k^2$ squares, called blocks, assigning each square to one machine. The vector segments are each sent to k machines, so there is a small additional cost in replicating the vector.
• Representing Blocks of a Transition Matrix : When we divide a transition matrix into square blocks, the columns are divided into k segments. To represent a segment of a column, nothing is needed if there are no nonzero entries in that segment. However, if there are one or more nonzero entries, then we need to represent the segment of the column by the total number of nonzero entries in the column (so we can tell what value the nonzero entries have) followed by a list of the rows with nonzero entries.
• Topic-Sensitive PageRank: If we know the queryer is interested in a certain topic, then it makes sense to bias the PageRank in favor of pages on that topic. To compute this form of PageRank, we identify a set of pages known to be on that topic, and we use it as a “teleport set.” The PageRank calculation is modified so that only the pages in the teleport set are given a share of the tax, rather than distributing the tax among
  all pages on the Web.
• Creating Teleport Sets: For topic-sensitive PageRank to work, we need to identify pages that are very likely to be about a given topic. One approach is to start with the pages that the open directory (DMOZ) identifies with that topic. Another is to identify words known to be associated with the topic, and select for the teleport set those pages that have an unusually high number of occurrences of such words.
• Link Spam: To fool the PageRank algorithm, unscrupulous actors have created spam farms. These are collections of pages whose purpose is to concentrate high PageRank on a particular target page.
• Structure of a Spam Farm: Typically, a spam farm consists of a target page and very many supporting pages. The target page links to all the supporting pages, and the supporting pages link only to the target page. In addition, it is essential that some links from outside the spam farm be created. For example, the spammer might introduce links to their target page by writing comments in other people’s blogs or discussion groups.
• TrustRank: One way to ameliorate the effect of link spam is to compute a topic-sensitive PageRank called TrustRank, where the teleport set is a collection of trusted pages. For example, the home pages of universities could serve as the trusted set. This technique avoids sharing the tax in the PageRank calculation with the large numbers of supporting pages in spam farms and thus preferentially reduces their PageRank.
• Spam Mass: To identify spam farms, we can compute both the conventional PageRank and the TrustRank for all pages. Those pages that have much lower TrustRank than PageRank are likely to be part of a spam farm.
• Hubs and Authorities: While PageRank gives a one-dimensional view of the importance of pages, an algorithm called HITS tries to measure two different aspects of importance. Authorities are those pages that contain valuable information. Hubs are pages that, while they do not themselves contain the information, link to places where the information can be found.
• Recursive Formulation of the HITS Algorithm: Calculation of the hubs and authorities scores for pages depends on solving the recursive equations: “a hub links to many authorities, and an authority is linked to by many hubs.” The solution to these equations is essentially an iterated matrix–vector multiplication, just like PageRank’s. However, the existence of dead ends or spider traps does not affect the solution to the HITS equations in the way they do for PageRank, so no taxation scheme is necessary.

END