GNN学习/GCN学习/GNN环境配置cuda安装/GCN代码展示

参考:

A Gentle Introduction to Graph Neural Networks https://distill.pub/2021/gnn-intro/
Understanding Convolutions on Graphs https://distill.pub/2021/understanding-gnns/
Graph neural networks: A review of methods and applications https://arxiv.org/pdf/1812.08434.pdf(没怎么看)
【零基础多图详解图神经网络（GNN/GCN）【论文精读】-哔哩哔哩】 https://b23.tv/1zxRCPD
【论文精讲】利用图神经网络进行阿尔兹海默症分类，基于神经影像模式融合，20小时带你快速学懂GNN原理模型及应用，超详细！！！-哔哩哔哩】 https://b23.tv/9bjwS2a
【简单粗暴带你快速理解GNN-哔哩哔哩】 https://b23.tv/drBKOzW
【【PyTorch】B站首个，终于有人把 GPU/ CUDA/ cuDNN 讲清楚了-哔哩哔哩】 https://b23.tv/ctxG5HQ

x.1 前言

相比较CNN假设的平移不变性是二维的，RNN假设的时序不变性是一维的，GNN假设的图的对称性是多维的。

1. CNN的平移不变性

CNN（卷积神经网络）的平移不变性指的是，当输入图像在平移时，CNN仍能识别出相同的特征和模式。

在卷积层中，卷积核通过滑动窗口的方式在输入图像上移动，对每个窗口进行卷积操作。由于卷积核的权重是固定的，因此当输入图像平移时，卷积核所卷积的图像区域也会相应地平移，从而保证了卷积操作的平移不变性。

通过具有平移不变性的卷积操作，CNN能够学习到对于输入图像中不同位置的相同特征的表示，从而使得其在识别目标时具有一定的位置不变性。这种位置不变性使得CNN在图像识别、目标检测等任务中表现出色。

2. RNN的时序不变性

RNN（循环神经网络）的时序不变性指的是，RNN能够对时序信息进行建模，并且其处理过程对输入序列的时间顺序不敏感，即具有不变性。

在RNN中，隐藏状态会保存之前输入的信息，并将其用于当前时间步的计算。因此，RNN在处理输入序列时会考虑到其时序关系，可以学习到输入序列中时间相关的模式和规律。然而，RNN的处理过程并不受输入序列的时间顺序影响，即输入序列的顺序可以任意调整，RNN仍将输出相同的结果。这种时序不变性使得RNN可以对具有不同时间顺序的输入序列进行建模，并且能够在不考虑时间顺序的情况下对其进行处理。

时序不变性使得RNN在处理自然语言处理、语音识别等需要考虑时序信息的任务时非常有用。例如，对于文本分类任务，可以将文本的句子顺序任意调整，而不影响RNN的分类结果。这种特性也为RNN在生成式任务中的应用提供了便利，如机器翻译、音乐生成等任务。

3. GNN的图的对称性

GNN（图神经网络）的图的对称性指的是，在一个无向图中，如果存在一种对称变换，可以将图中的任意两个节点进行交换而不改变图的结构，则该图具有对称性。

通过上面的3种神经网络假设性质的对比，发现图的应用范围更多维，例如社交网络，推荐算法等等。

x.2 对GNN的大致解释

而如何简单粗暴理解GNN（Graph Neural Networks）呢，你可以想象GNN为一个MLP，它可以大致分为三个主要部分：输入层，隐藏层和输出层。其中隐藏层通常由多个GCN（Graph Convolutional Network）组成。而GCN则主要由聚合（Aggregation），更新（Update)和多层（Multi-layer）。

在GCN中，聚合、更新和循环分别指以下几个步骤：

聚合（Aggregation）：将邻居节点的信息进行聚合并加权得到当前节点的表征向量。
更新（Update）：将当前节点的表征向量与其它特征（例如节点属性）结合起来，更新当前节点的表征向量。
多层（Multi-layer）：为了捕获不同层次的节点特征，通常需要将上述两个步骤叠加多次。这些步骤的重复层数可以根据问题的复杂程度和计算资源的可用性来确定。

在每一层GCN中，聚合操作和更新操作都是可学习的。因此，每个GCN层可以学习到不同的邻居聚合策略和节点更新规则，从而提高整个网络的表征能力。

为了方便理解，我们将Aggregation，Update和Multi-layer再以图片的形式理解一遍：

Aggregation

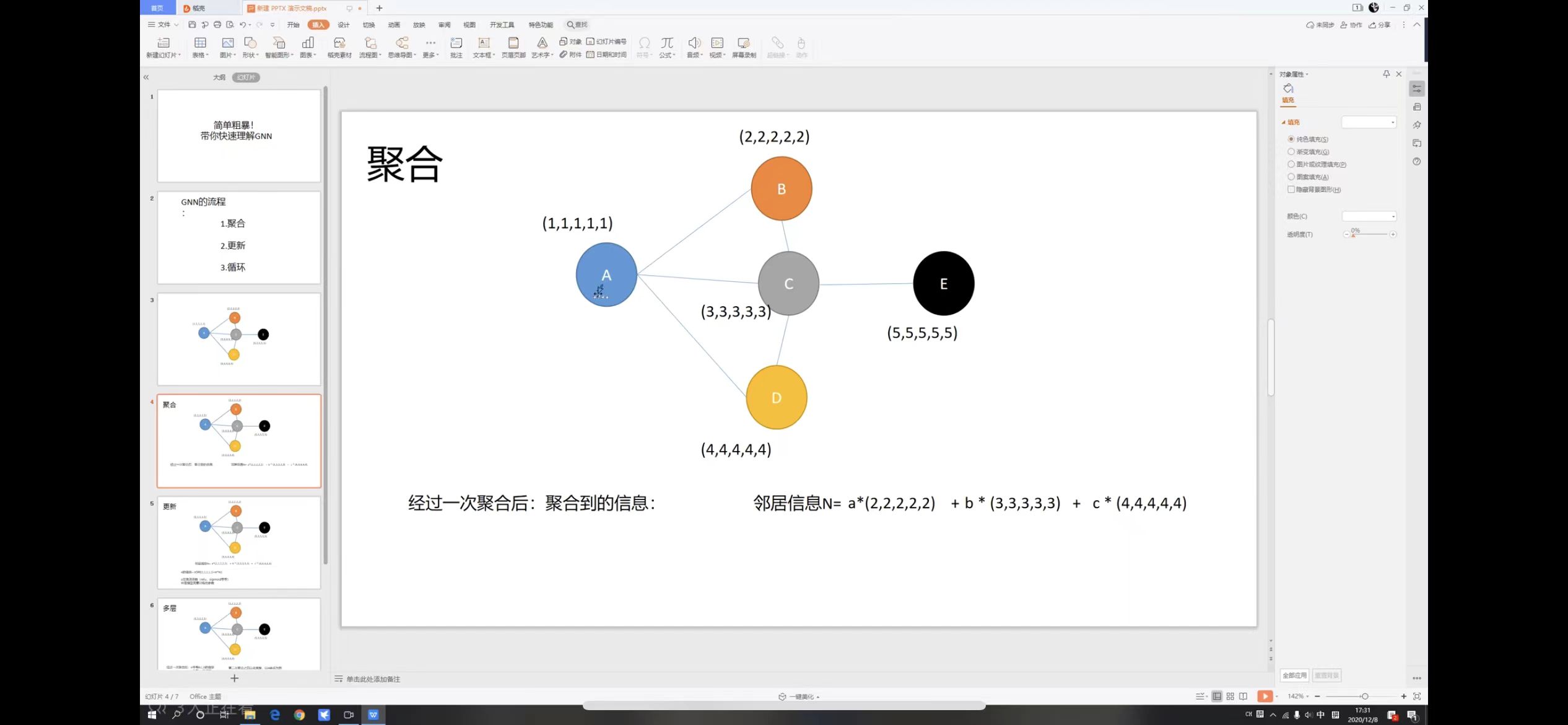
在这里插入图片描述

如上图所示，例如对于节点A，它所连的节点有B，C，D，我们需要将A的相邻节点乘以对应的权重值，得到A的聚合信息即N。

Update

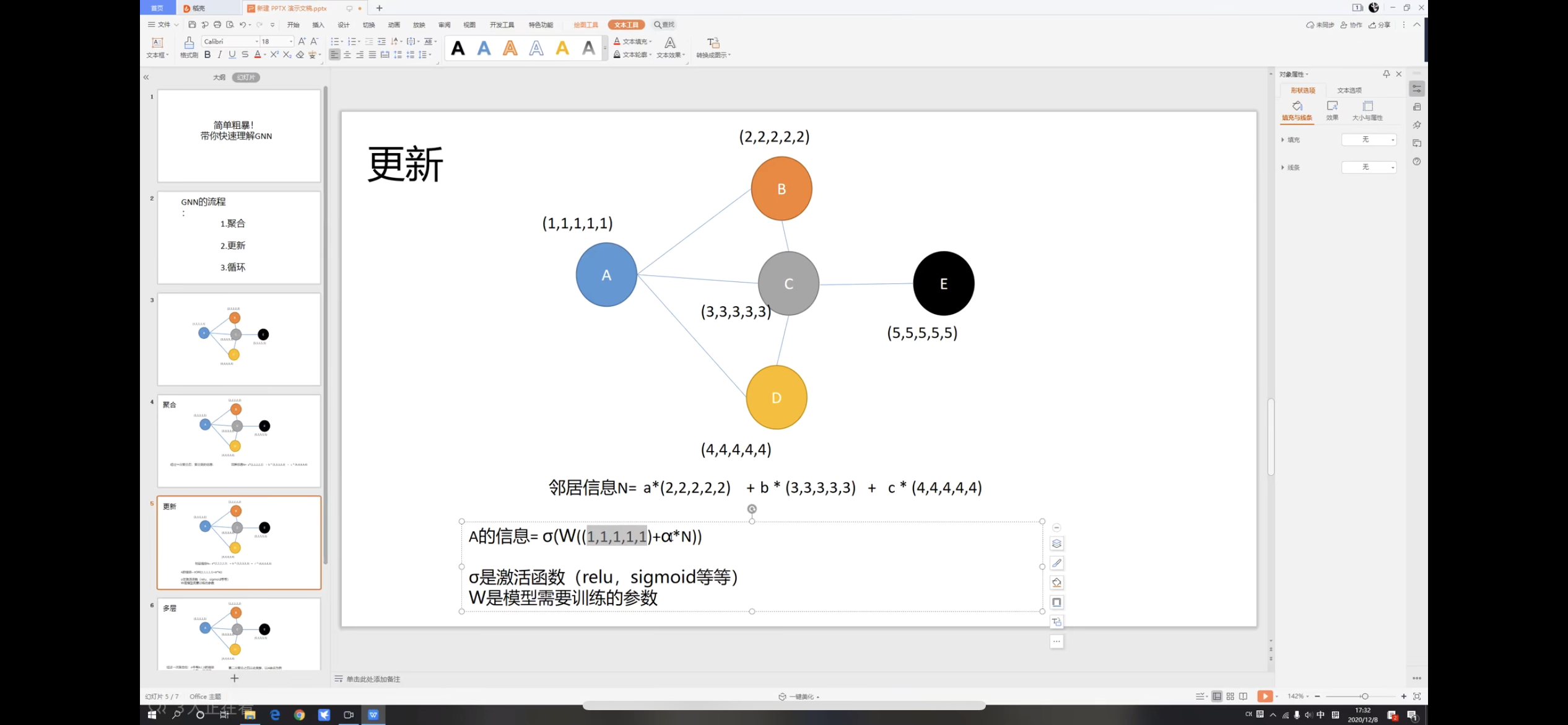
在这里插入图片描述

如上图所示我们将A和上一步得到的聚合信息N做一些数学处理，得到了A的更新信息。

Multi-layer

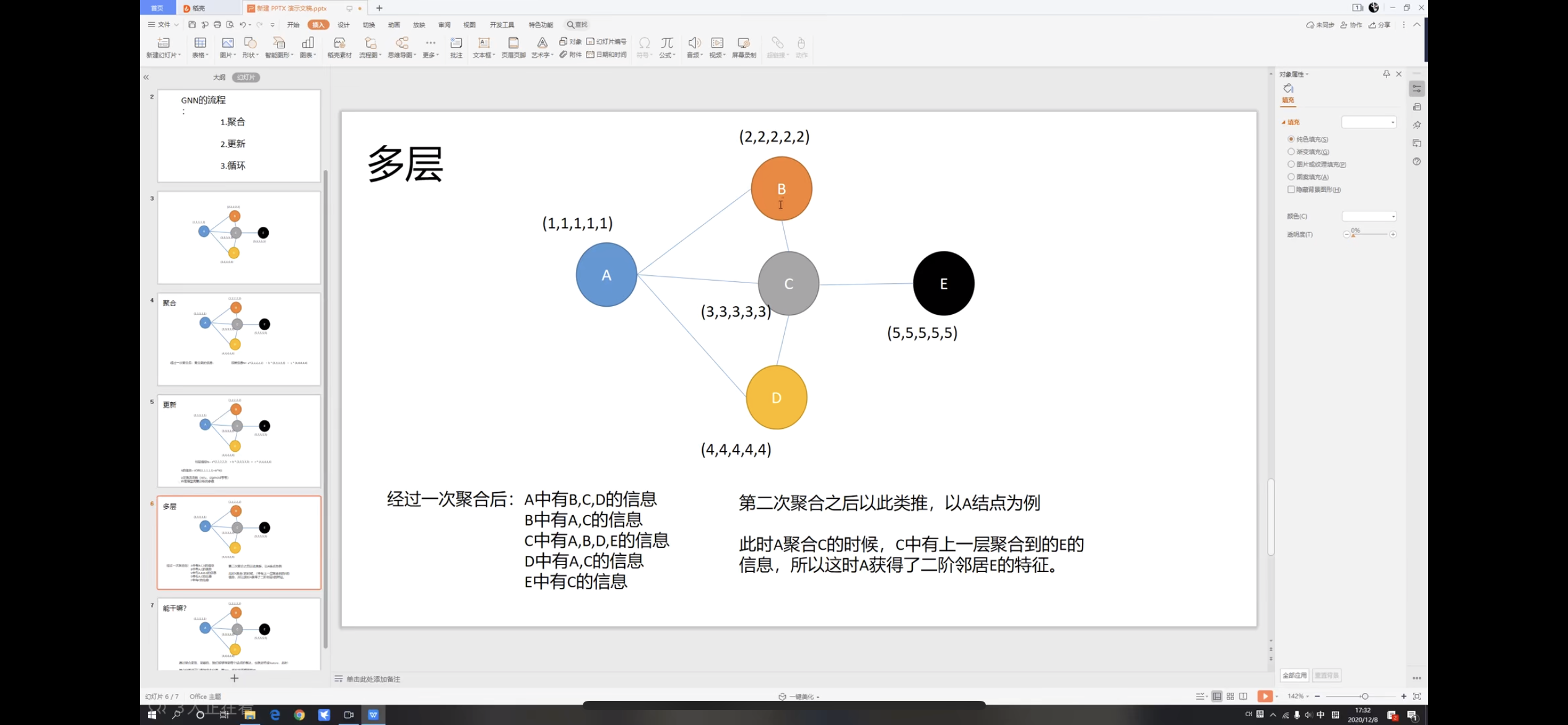
在这里插入图片描述

如上图所示，每一次循环后都会得到上一层的更多节点的信息，最终几乎能得到其余节点的全部信息。

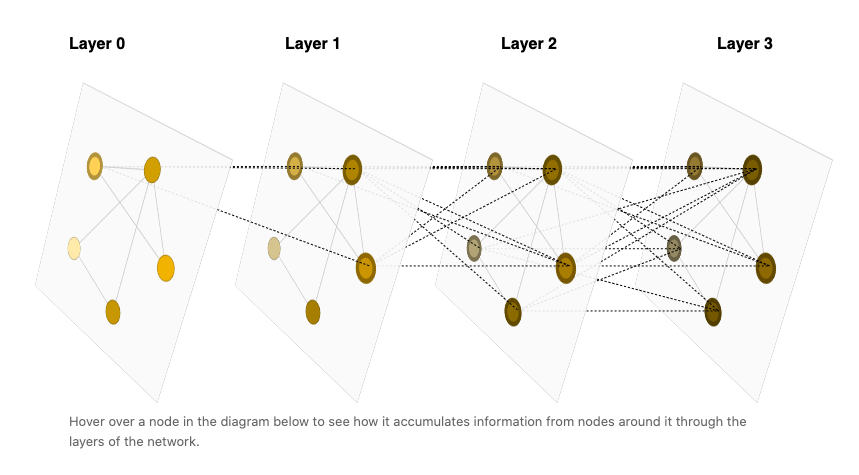
请添加图片描述

GNN就是对邻近节点的特征信息进行融合，在了解了大致框架后，对后续GNN的理解会简单的多。

x.3 GNN的前储知识::图知识

和数据结构中的图的知识如出一辙，邻接矩阵是比较重要的，邻接表的链式表达和GNN中的邻接表没有太多关系。待补充

x.4 GNN的前储知识::数学知识

主要使用了Fourier transformation（傅里叶变换）和laplacian（拉普拉斯算子），这和数字图像处理的知识差不离。待补充。

x.5 GCN介绍

x.5.1 GCN的一些基本术语

请添加图片描述

A是左边这个图的邻接矩阵， $I_N$ 是单位矩阵， $\tilde{A} = A+I_N$ 即是增加了自身到自身连线的邻接矩阵， $\tilde{D}$ 则是将每一行的度相加到对角线上， $\tilde{D}^{-\frac{1}{2}}$ 是将对角线元素求倒数后再开方得到的矩阵；

$H^{(l)}$ 是指输入的本层的所有的点（每一行是一个点的特征向量）的特征矩阵， $H^{(l+1)}$ 是指输出的点的特征矩阵， $W^{(l)}$ 是指可学习的参数。

在公式2的计算公式如下：

请添加图片描述

x.5.2 GCN计算实例

以下图二为例，点1,2,3组成了特征矩阵，对于公式解释如下：

$A H$ 表示H聚合它周围节点的特征
$\tilde{A}H$ 表示H聚合它周围节点的特征，再加节点本身的信息
$D A D$ 指做归一化

请添加图片描述

x.5.3 GCN多层

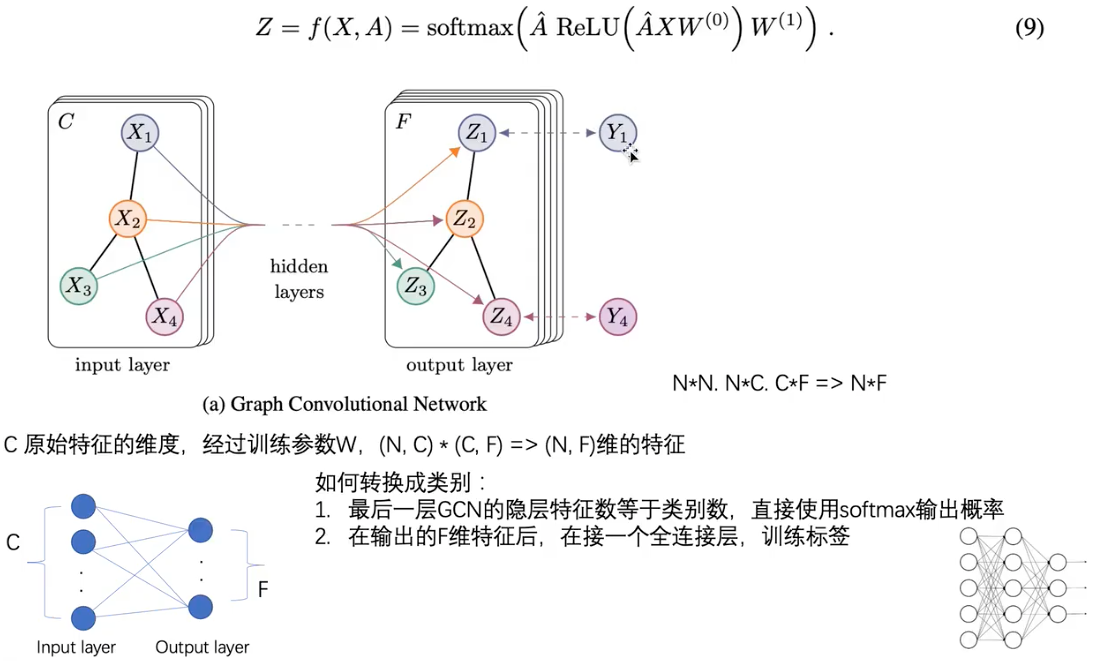
请添加图片描述

GCN的使用类似MLP，input layer做输入，多层hidden layer，output layer做输出，输入输出中图的结构不改变，但是节点的特征向量被改变了。最终NxC维度的特征向量变成了NxF维度的特征向量。

x.6 GNN环境配置cuda安装

待补充。

GNN环境配置，conda文件安装，pip安装，使用.whl文件安装

安装带有cuda的pytorch pip install torch==1.11.0+cu113 --extra-index-url https://download.pytorch.org/whl/cu113

x.7 GCN代码展示

这里采用的是pygcn的代码https://github.com/tkipf/pygcn

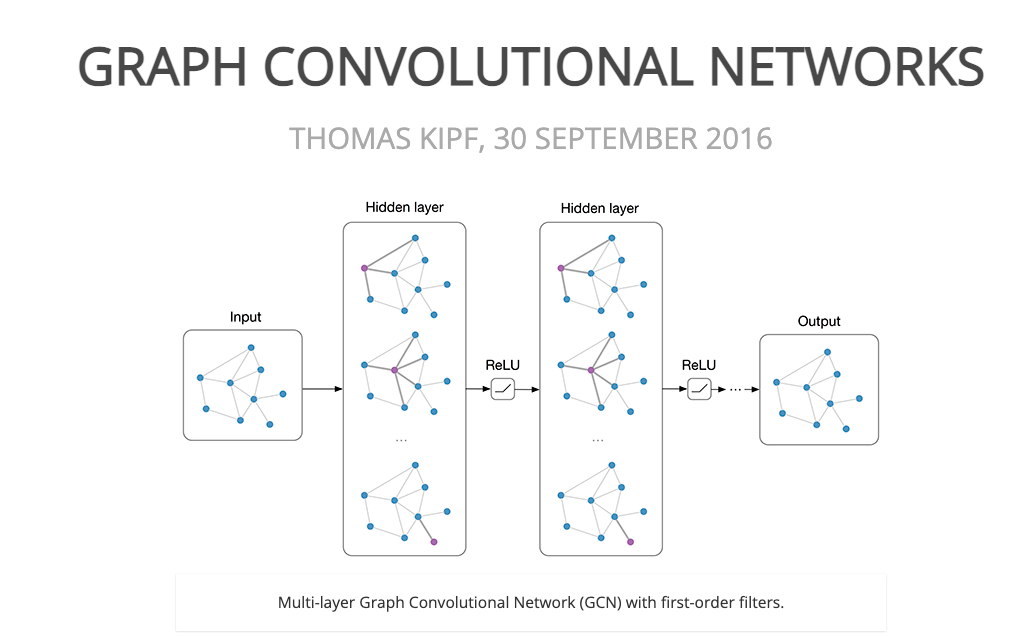
在这里插入图片描述

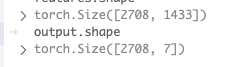
在这个代码的数据集中cora.cites保存的是边的连接信息；cora.content保存的是点和邻接矩阵的信息，其中第一列是点的序号，最后一列是label标签，从[1:-1]是邻接矩阵，我们通过下式计算最终点的输出。

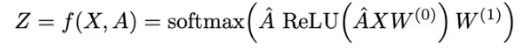
请添加图片描述

最终我们通过网络输入[2708, 1433]的信息，输出[2708, 7]的信息，其中2708为样本数量batch_size，7为最终的类别数。

请添加图片描述

x.7.1 torch.nn.parameter是什么函数，如何使用，例子

torch.nn.Parameter是一个类，用于将张量标记为模型的参数。在训练期间，这些参数可以被优化器调整以最小化损失函数。下面是一个例子，说明如何使用torch.nn.Parameter来创建一个简单的线性模型：

import torch
import torch.nn as nn

class LinearModel(nn.Module):
    def __init__(self, input_size, output_size):
        super(LinearModel, self).__init__()
        self.weight = nn.Parameter(torch.randn(output_size, input_size))
        self.bias = nn.Parameter(torch.randn(output_size))

    def forward(self, input):
        return torch.matmul(input, self.weight.t()) + self.bias

在这个例子中，LinearModel是一个简单的线性模型，它有一个权重矩阵和一个偏置向量。在__init__方法中，我们使用nn.Parameter来将这些张量标记为模型的参数。在模型的前向传递过程中，我们使用这些参数来计算模型的输出。

下面是一个使用LinearModel的例子：

input_size = 5
output_size = 2
batch_size = 10

model = LinearModel(input_size, output_size)
input = torch.randn(batch_size, input_size)
output = model(input)

print(output.shape)

在这个例子中，我们创建了一个LinearModel对象，并将它应用于一批大小为batch_size的输入张量。我们打印输出张量的形状，以确认输出张量的形状为(batch_size, output_size)。

x.7.2 torch.spmm是什么意思，例子

torch.spmm是PyTorch中用于执行稀疏矩阵乘法的函数。它接受三个参数：稀疏矩阵、密集矩阵和一个可选的beta参数，用于控制输出与之前的累加权重。它返回一个密集矩阵，其形状为稀疏矩阵的行数和密集矩阵的列数。

以下是一个使用torch.spmm函数的简单示例：

import torch

# 创建稀疏矩阵
sparse_mat = torch.sparse_coo_tensor(
    indices=[[0, 1, 1], [2, 0, 1]],
    values=[3, 4, 5],
    size=(2, 3)
)

# 创建密集矩阵
dense_mat = torch.tensor([[1, 2], [3, 4], [5, 6]])

# 使用torch.spmm函数执行稀疏矩阵乘法
result = torch.spmm(sparse_mat, dense_mat)

print(result)

在这个示例中，我们首先创建了一个形状为(2, 3)的稀疏矩阵sparse_mat，然后创建了一个形状为(3, 2)的密集矩阵dense_mat。我们将这两个矩阵传递给torch.spmm函数，以获得一个形状为(2, 2)的密集矩阵result。这个结果矩阵是由稀疏矩阵sparse_mat和密集矩阵dense_mat相乘得到的。

x.7.3 如何打印稀疏矩阵sparse_mat

import torch

# 创建稀疏矩阵
sparse_mat = torch.sparse_coo_tensor(
    indices=[[0, 1, 1], [2, 0, 1]],
    values=[3, 4, 5],
    size=(2, 3)
)

# 将稀疏矩阵转换为密集矩阵并打印结果
print(sparse_mat.to_dense())