D和R的关系
高分辨率量化
- 均匀量化:量化区间 ‘ Δ k = y k − y k − 1 ‘ `\Delta_k=y_k-y_{k-1}` ‘Δk=yk−yk−1‘,近似为常数;p(x)为信源概率密度函数,且 ‘ Δ k ‘ `\Delta_k` ‘Δk‘的大小相对于p(x)的变化率充分小,此时 ‘ p ( x ) = p k Δ k , x ∈ ( y k − 1 , y k ] , p k = P r { X ∈ ( y k − 1 , y k ] } ‘ `p(x)=\frac{p_k}{\Delta_k},x\in(y_{k-1},y_k], p_k=Pr\{{X\in(y_{k-1},y_k]}\}` ‘p(x)=Δkpk,x∈(yk−1,yk],pk=Pr{X∈(yk−1,yk]}‘
‘ D = M S E = ∑ k = 1 K ∫ y k − 1 y k ( x − x k ) 2 p ( x ) d x = ∑ k = 1 K ∫ x k − Δ k / 2 x k + Δ k / 2 ( x − x k ) 2 p ( x ) d x = ∑ k = 1 K p k Δ k ∫ x k − Δ k / 2 x k + Δ k / 2 ( x − x k ) 2 d x = ∑ k = 1 K p k Δ k ∫ − Δ k / 2 Δ k / 2 x 2 d x = 1 12 ∑ k = 1 K p k Δ k 2 = Δ 2 12 , 对于均匀量化器, Δ k = y k − y k − 1 = Δ , 1 < = k < = K ‘ ` \begin{aligned} D=MSE&=\displaystyle \sum^{K}_{k=1}\int_{y_{k-1}}^{y_k}(x-x_k)^2p(x)dx \\ &=\displaystyle \sum^{K}_{k=1}\int_{x_k-\Delta_k/2}^{x_k+\Delta_k/2}(x-x_k)^2p(x)dx \\ &=\displaystyle \sum^{K}_{k=1}\frac{p_k}{\Delta_k}\int_{x_k-\Delta_k/2}^{x_k+\Delta_k/2}(x-x_k)^2dx \\ &= \displaystyle \sum^{K}_{k=1}\frac{p_k}{\Delta_k}\int_{-\Delta_k/2}^{\Delta_k/2}x^2dx \\ &=\frac{1}{12}\sum^{K}_{k=1} p_k {\Delta_k}^2 \\ &=\frac{\Delta^2}{12},对于均匀量化器,\Delta_k=y_k-y_{k-1}=\Delta,1<=k<=K \end{aligned} ` ‘D=MSE=k=1∑K∫yk−1yk(x−xk)2p(x)dx=k=1∑K∫xk−Δk/2xk+Δk/2(x−xk)2p(x)dx=k=1∑KΔkpk∫xk−Δk/2xk+Δk/2(x−xk)2dx=k=1∑KΔkpk∫−Δk/2Δk/2x2dx=121k=1∑KpkΔk2=12Δ2,对于均匀量化器,Δk=yk−yk−1=Δ,1<=k<=K‘
- 熵限制的量化:对于固定失真D,编码量化值 ‘ X ‾ = Q ( x ) ‘ `\overline X=Q(x)` ‘X=Q(x)‘所需的比特最小值是熵 ‘ H ( X ‾ ) ‘ `H(\overline X)` ‘H(X)‘
‘ p k = P r ( X ‾ = x k ) = P r ( X ∈ ( y k − 1 , y k ] ) = ∫ y k − 1 y k p ( x ) d x p k = p ( x ) Δ k H ( X ‾ ) = − ∑ k = 1 K p k log 2 p k = − ∑ k = 1 K ∫ y k − 1 y k p ( x ) ( log 2 p ( x ) + log 2 Δ k ) d x = − ∑ k = 1 K ∫ y k − 1 y k p ( x ) log 2 p ( x ) d x − ∑ k = 1 K ∫ y k − 1 y k p ( x ) log 2 Δ k d x = − ∑ k = 1 K ∫ y k − 1 y k p ( x ) log 2 p ( x ) d x − ∑ k = 1 K p k log 2 Δ k = H d ( X ) − 1 2 ∑ k = 1 K p k log 2 Δ k 2 因为 log 2 是凹函数 , 在高分辨率量化假设下 1 2 ∑ k = 1 K p k log 2 Δ k 2 < = 1 2 log 2 ∑ k = 1 K p k Δ k 2 = 1 2 log 2 12 D 所以 H ( X ‾ ) > = H d ( X ) − 1 2 log 2 ( 12 D ) , 当前仅当所有 Δ k 相等时,不等式相等 针对高分辨率量化器,最小平均比特 R = H ( X ‾ ) = H d ( X ) − 1 2 log 2 12 D , 可以得到 D = 2 2 H d ( X ) 12 ∗ 2 − 2 R = b ∗ 2 − R / a , 其中 b = 2 2 H d ( X ) 12 , a = 1 2 ‘ ` \begin{aligned} p_k&=Pr(\overline X=x_k)=Pr(X\in(y_{k-1},y_k]) =\int_{y_{k-1}}^{y_k} p(x)dx \\ p_k&=p(x)\Delta_k \\ H(\overline X) &=-\displaystyle \sum^{K}_{k=1}p_k \log_{2}{p_k} \\ &= -\displaystyle \sum^{K}_{k=1} \int_{y_{k-1}}^{y_k} p(x)(\log_2{p(x)+\log_2{\Delta_k}})dx \\ &= -\displaystyle \sum^{K}_{k=1} \int_{y_{k-1}}^{y_k} p(x)\log_2{p(x})dx - \displaystyle \sum^{K}_{k=1} \int_{y_{k-1}}^{y_k} p(x)\log_2{\Delta_k}dx \\ &= -\displaystyle \sum^{K}_{k=1} \int_{y_{k-1}}^{y_k} p(x)\log_2{p(x})dx -\displaystyle \sum^{K}_{k=1} p_k \log_2{\Delta_k} \\ &= H_d(X) - \frac{1}{2}\displaystyle \sum^{K}_{k=1} p_k \log_2{\Delta_k}^2 \\ & 因为\log_2是凹函数,在高分辨率量化假设下 \\ &\frac{1}{2}\displaystyle \sum^{K}_{k=1} p_k \log_2{\Delta_k}^2 <=\frac{1}{2} \log_2{\displaystyle \sum^{K}_{k=1} p_k\Delta_k^2}=\frac{1}{2} \log_2{12D} \\ & 所以 \\ & H(\overline X) >= H_d(X) - \frac{1}{2} \log_2(12D), 当前仅当所有\Delta_k相等时,不等式相等 \\ & 针对高分辨率量化器,最小平均比特R=H(\overline X)=H_d(X)-\frac{1}{2}\log_2{12D},可以得到 \\ D&=\frac{2^{2H_d(X)}}{12}* 2^{-2R}=b*2^{-R/a},其中b=\frac{2^{2H_d(X)}}{12}, a = \frac{1}{2} \end{aligned} ` ‘pkpkH(X)D=Pr(X=xk)=Pr(X∈(yk−1,yk])=∫yk−1ykp(x)dx=p(x)Δk=−k=1∑Kpklog2pk=−k=1∑K∫yk−1ykp(x)(log2p(x)+log2Δk)dx=−k=1∑K∫yk−1ykp(x)log2p(x)dx−k=1∑K∫yk−1ykp(x)log2Δkdx=−k=1∑K∫yk−1ykp(x)log2p(x)dx−k=1∑Kpklog2Δk=Hd(X)−21k=1∑Kpklog2Δk2因为log2是凹函数,在高分辨率量化假设下21k=1∑Kpklog2Δk2<=21log2k=1∑KpkΔk2=21log212D所以H(X)>=Hd(X)−21log2(12D),当前仅当所有Δk相等时,不等式相等针对高分辨率量化器,最小平均比特R=H(X)=Hd(X)−21log212D,可以得到=1222Hd(X)∗2−2R=b∗2−R/a,其中b=1222Hd(X),a=21‘
《信号处理的小波导引》第11.2节
《Principles of Digital Communication》chapter 3: https://ocw.mit.edu/courses/6-450-principles-of-digital-communications-i-fall-2006/926689aaa62a0315473fa9b982de1b07_book_3.pdf
lambda
hm lambda2推导
‘ D = b ∗ 2 ( − R / a ) R = a l o g 2 ( b D ) D = Q s t e p 2 12 ,为了体现 Q s t e p 和 Q P 的关系,这里用 Q s t e p 替换 Δ Q s t e p = 2 ( Q P − 4 ) / 6 D = 2 ( Q P − 4 ) / 3 12 d D d Q P = d ( 2 ( Q P − 4 ) / 3 ) 12 d Q P = 1 12 ⋅ 2 ( Q P − 4 ) / 3 ⋅ l n 2 = l n 2 ⋅ 1 3 ⋅ 1 4 ⋅ 2 ( Q P − 4 ) / 3 = l n 2 3 ⋅ 2 ( Q P − 4 ) / 3 − 2 = l n 2 3 2 ( Q P − 10 ) / 3 = l n 2 24 Q s t e p 2 d R d Q P = d ( a l o g 2 ( b D ) ) d Q P = a ( d l o g 2 ( b D ) d D d D d Q P ) = a 2 ( Q P − 4 ) / 3 12 b 1 l n 2 d ( b D ) d D d D d Q P = a 2 ( Q P − 4 ) / 3 12 b 1 l n 2 ⋅ ( − b D − 2 ) ) d D d Q P = a 2 ( Q P − 4 ) / 3 12 b − b l n 2 12 ⋅ 12 2 ( Q P − 4 ) / 3 ⋅ 2 ( Q P − 4 ) / 3 d D d Q P = a 2 ( Q P − 4 ) / 3 12 b − b l n 2 12 ⋅ 12 2 ( Q P − 4 ) / 3 ⋅ 2 ( Q P − 4 ) / 3 ⋅ 1 12 ⋅ 2 ( Q P − 4 ) / 3 ⋅ l n 2 = − a 3 J = D + λ R d J d R = d D d R + λ = 0 λ = − d D d Q P d R d Q P = − l n 2 24 Q s t e p 2 − a 3 = l n 2 8 a Q s t e p 2 l n 2 ≈ 2 − 2 / 3 λ = − d D d Q P d R d Q P = − l n 2 3 2 ( Q P − 10 ) / 3 − a 3 = l n 2 ⋅ 2 ( Q P − 10 ) / 3 a = c ⋅ 2 ( Q P − 12 ) / 3 ‘ ‘ ` \begin{aligned} & D=b*2^{(-R/a)} \\ & R=alog_2(\frac{b}{D}) \\ & D=\frac{Qstep^2}{12},为了体现Qstep和QP的关系,这里用Qstep替换\Delta \\ & Qstep=2^{(QP-4)/6} \\ & D=\frac{2^{(QP-4)/3}}{12} \\ & \frac{dD}{dQP}=\frac{\frac{d(2^{(QP-4)/3})}{12}}{dQP}=\frac{1}{12}\cdot2^{(QP-4)/3}\cdot ln2=ln2\cdot\frac{1}{3}\cdot\frac{1}{4}\cdot2^{(QP-4)/3}=\frac{ln2}{3}\cdot2^{(QP-4)/3-2}=\frac{ln2}{3}2^{(QP-10)/3}=\frac{ln2}{24}Qstep^2 \\ & \frac{dR}{dQP}=\frac{d(alog_2(\frac{b}{D}))}{dQP}=a(\frac{dlog_2(\frac{b}{D})}{dD}\frac{dD}{dQP})=a\frac{2^{(QP-4)/3}}{12b}\frac{1}{ln2}\frac{d(\frac{b}{D})}{dD}\frac{dD}{dQP} \\ & =a\frac{2^{(QP-4)/3}}{12b}\frac{1}{ln2}\cdot(-bD^{-2}))\frac{dD}{dQP}=a\frac{2^{(QP-4)/3}}{12b}\frac{-b}{ln2}\frac{12\cdot12}{2^{(QP-4)/3}\cdot2^{(QP-4)/3}}\frac{dD}{dQP} \\ & =a\frac{2^{(QP-4)/3}}{12b}\frac{-b}{ln2}\frac{12\cdot12}{2^{(QP-4)/3}\cdot2^{(QP-4)/3}}\cdot \frac{1}{12}\cdot2^{(QP-4)/3}\cdot ln2=-\frac{a}{3} \\ & J=D + \lambda R \\ & \frac{dJ}{dR}=\frac{dD}{dR}+\lambda=0 \\ & \lambda= -\frac{\frac{dD}{dQP}}{\frac{dR}{dQP}}=\frac{-\frac{ln2}{24}Qstep^2}{-\frac{a}{3}}=\frac{ln2}{8 a}Qstep^2 \\ & ln2\approx 2^{-2/3} \\ & \lambda= -\frac{\frac{dD}{dQP}}{\frac{dR}{dQP}}=\frac{-\frac{ln2}{3}2^{(QP-10)/3}}{-\frac{a}{3}}=\frac{ln2\cdot{2^{(QP-10)/3}}}{a}=c \cdot 2^{(QP-12)/3}` \\ \end{aligned} ` ‘D=b∗2(−R/a)R=alog2(Db)D=12Qstep2,为了体现Qstep和QP的关系,这里用Qstep替换ΔQstep=2(QP−4)/6D=122(QP−4)/3dQPdD=dQP12d(2(QP−4)/3)=121⋅2(QP−4)/3⋅ln2=ln2⋅31⋅41⋅2(QP−4)/3=3ln2⋅2(QP−4)/3−2=3ln22(QP−10)/3=24ln2Qstep2dQPdR=dQPd(alog2(Db))=a(dDdlog2(Db)dQPdD)=a12b2(QP−4)/3ln21dDd(Db)dQPdD=a12b2(QP−4)/3ln21⋅(−bD−2))dQPdD=a12b2(QP−4)/3ln2−b2(QP−4)/3⋅2(QP−4)/312⋅12dQPdD=a12b2(QP−4)/3ln2−b2(QP−4)/3⋅2(QP−4)/312⋅12⋅121⋅2(QP−4)/3⋅ln2=−3aJ=D+λRdRdJ=dRdD+λ=0λ=−dQPdRdQPdD=−3a−24ln2Qstep2=8aln2Qstep2ln2≈2−2/3λ=−dQPdRdQPdD=−3a−3ln22(QP−10)/3=aln2⋅2(QP−10)/3=c⋅2(QP−12)/3‘‘
实际使用:
‘ l a m b d a 2 = 2 ( Q P − 12 ) / 3 ‘ `lambda2= 2^{(QP-12)/3}` ‘lambda2=2(QP−12)/3‘
‘ l a m b d a = 2 ( Q P − 12 ) / 6 ‘ `lambda = 2^{(QP-12)/6}` ‘lambda=2(QP−12)/6‘
《Implementing rate-distortion optimization on a resource-limited H.264 encoder》第3.3节
《新一代高效视频编码H.265HEVC原理、标准与实现》第170页
x265 lambda2推导
‘ Q P = 4.2005 × l n ( λ ) + 13.7122 ‘ `QP=4.2005 \times ln(\lambda) + 13.7122` ‘QP=4.2005×ln(λ)+13.7122‘
‘ Q P − 13.7122 4.2005 = l n ( λ ) ‘ `\frac {QP - 13.7122}{4.2005}=ln(\lambda)` ‘4.2005QP−13.7122=ln(λ)‘
‘ λ = e Q P 4.2005 ⋅ e − 13.7122 4.2005 ‘ `\lambda=e^{\frac{QP}{4.2005}} \cdot e^{\frac{-13.7122}{4.2005}}` ‘λ=e4.2005QP⋅e4.2005−13.7122‘
实际使用:
‘ l a m b d a 2 = 0.038 ⋅ e 0.238 ⋅ Q P ‘ `lambda2 = 0.038 \cdot e^{0.238 \cdot QP}` ‘lambda2=0.038⋅e0.238⋅QP‘
‘ l a m b d a = 2 ( Q P − 12 ) / 6 ‘ `lambda = 2^{(QP-12)/6}` ‘lambda=2(QP−12)/6‘
《面向高性能视频编码标准的率失真优化技术研究》,李斌,中科大博士论文,第5章
x264 lambda2推导
实际使用:
‘ l a m b d a 2 = 0.9 ∗ 2 ( Q P − 12 ) / 3 ‘ `lambda2 = 0.9*2^{(QP-12)/3}` ‘lambda2=0.9∗2(QP−12)/3‘
‘ l a m b d a = 2 ( Q P − 12 ) / 6 ‘ `lambda = 2^{(QP-12)/6}` ‘lambda=2(QP−12)/6‘
x264和x265码控
码控公式
- RD曲线中码率,失真是通过QP来调节
- 图像复杂度不变,量化步长越小码率越大,反之越小
- 量化步长不变,码率和复杂度成正比
- 预分析中使用SATD衡量失真,所以,在计算cost的时候使用qscale= ‘ λ ‘ `\sqrt{\lambda}` ‘λ‘,作为拉格朗日乘子,该值和Qstep存在线性关系
‘ q s c a l e ∝ X R q s c a l e = α ∗ X R = X R / α = X r a t e F a c t o r Q P = 12 + 6 ∗ log 2 q s c a l e 0.85 ‘ ` \begin{aligned} &qscale\propto\frac{X}{R} \\ &qscale=\alpha*\frac{X}{R}=\frac{X}{R/\alpha}=\frac{X}{rateFactor} \\ &QP=12+6*\log_{2}{\frac{qscale}{0.85}} \end{aligned} ` ‘qscale∝RXqscale=α∗RX=R/αX=rateFactorXQP=12+6∗log20.85qscale‘
从公式上看,qscale等价于lambda
在使用时,只需要算出X、rateFactor就可以计算出编码当前帧的qscale,然后算出QP
计算X
模糊复杂度
-
每一帧的复杂度用SATD表示
-
为了避免QP波动过大,使用模糊复杂度,也就是使用前面帧的SATD进行平滑
‘ b l u r r e d C o m p l e x i t y = { f p s / 25 , c u t r e e = 1 & & a q = 0 s h o r t T e r m C p l x S u m s h o r t T e r m C p l x C o u n t = ∑ i = 0 n 0. 5 n − i ∗ c u r r e n t S a t d i ∑ i = 0 n 0. 5 n − i , 其他 ‘ ` \begin{aligned} blurredComplexity= \begin{cases} fps/25, cutree=1 \&\& aq=0 \\ \frac{shortTermCplxSum}{shortTermCplxCount}=\frac{\displaystyle \sum^{n}_{i=0}0.5^{n-i}*currentSatd_i}{\displaystyle \sum^{n}_{i=0}0.5^{n-i}}, 其他 \\ \end{cases} \end{aligned} ` ‘blurredComplexity=⎩ ⎨ ⎧fps/25,cutree=1&&aq=0shortTermCplxCountshortTermCplxSum=i=0∑n0.5n−ii=0∑n0.5n−i∗currentSatdi,其他‘
感知编码优化
You want the movie to be somewhere approaching constant quality. However, constant quality does not mean constant PSNR nor constant QP.Details are less noticeable in high-complexity or high-motion scenes, so you can get away with somewhat higher QP for the same perceived quality”恒定的质量并不代表恒定的QP, 对于高复杂度的场景,细节丢失比较难以发现,因此可以使用比较高的QP.所以对复杂度进行了非线性压缩
‘ X = b l u r r e d C o m p l e x i t y 1 − r c . q C o m p r e s s ‘ `X=blurredComplexity^{1-rc.qCompress}` ‘X=blurredComplexity1−rc.qCompress‘
- rc.qCompress = 0, qscale 与复杂度成正比,分配给平缓的帧和复杂的帧的比特是一样的,行为接近CBR
- rc.qCompress = 1, qscale 与复杂度无关(各帧QP相等), 码率与复杂度成正比。相当于关闭了此项感知编码优化
经过如上的计算X=rceq
计算rateFactor
CRF
‘ b a s e C p l x = { m n c u ∗ 120 , b f r a m e s > 0 m n c u ∗ 80 , b f r a m e s = 0 m b t r e e _ o f f s e t = { ( 1.0 − r c . q C o m p r e s s ) ∗ 13.5 , r c . c u T r e e = 1 0 , r c . c u T r e e = 0 m _ q C o m p r e s s = { 1 , ! r c . h e v c A q & & r c . c u T r e e r c . q C o m p r e s s , o t h e r s r a t e F a c t o r = X q s c a l e = r a t e F a c t o r C o n s t a n t = b a s e C p l x 1 − m _ q C o m p r e s s x 265 _ q p 2 q S c a l e ( r c . r f C o n s t a n t + m b t r e e _ o f f s e t ) ‘ ` \begin{aligned} &baseCplx= \begin{cases} m_ncu * 120, bframes>0 \\ m_ncu * 80, bframes=0 \\ \end{cases} \\ &mbtree\_offset= \begin{cases} (1.0 - rc.qCompress) * 13.5, rc.cuTree=1 \\ 0, rc.cuTree=0 \\ \end{cases} \\ &m\_qCompress= \begin{cases} 1, !rc.hevcAq \&\&rc.cuTree \\ rc.qCompress, others \end{cases} \\ &rateFactor=\frac{X}{qscale}=rateFactorConstant= \frac{baseCplx^{1 - m\_qCompress}}{ x265\_qp2qScale(rc.rfConstant + mbtree\_offset)} \end{aligned} ` ‘baseCplx={mncu∗120,bframes>0mncu∗80,bframes=0mbtree_offset={(1.0−rc.qCompress)∗13.5,rc.cuTree=10,rc.cuTree=0m_qCompress={1,!rc.hevcAq&&rc.cuTreerc.qCompress,othersrateFactor=qscaleX=rateFactorConstant=x265_qp2qScale(rc.rfConstant+mbtree_offset)baseCplx1−m_qCompress‘
ABR
计算 ‘ α ‘ `\alpha` ‘α‘
‘ α = q s c a l e ∗ R X ‘ `\alpha=\frac{qscale*R}{X}` ‘α=Xqscale∗R‘
因为 ‘ α ‘ `\alpha` ‘α‘不是一个固定的值,所以,可以通过前面已编码的帧进行迭代更新
‘ α = ∑ i = 0 n − 1 b i t i ∗ q s c a l e i r c e q i ‘ `\alpha=\displaystyle \sum^{n-1}_{i=0}\frac{bit_{i}*qscale_{i}}{rceq_{i}}` ‘α=i=0∑n−1rceqibiti∗qscalei‘
- ‘ r c e q i ‘ `rceq_i` ‘rceqi‘表示已编码帧的复杂度X
- ‘ q s c a l e i ‘ `qscale_i` ‘qscalei‘表示已编码帧的qscale
- ‘ b i t s i ‘ `bits_i` ‘bitsi‘表示已编码帧的真实比特R
- 初始化时, ‘ α = 0.01 ∗ ( 7 ∗ 1 0 5 ) q c o m p ∗ M b C o u n t ‘ `\alpha=0.01*(7*10^5)^{qcomp}*\sqrt{MbCount}` ‘α=0.01∗(7∗105)qcomp∗MbCount‘
计算R
- ‘ R = ∑ i = 0 n b i t r a t e f p s ‘ `\displaystyle R=\sum^{n}_{i=0}\frac{bitrate}{fps}` ‘R=i=0∑nfpsbitrate‘
‘ r a t e F a c t o r = R α = w a n t e d _ b i t s _ w i n d o w i c p l x r _ s u m i = w a n t e d _ b i t s _ w i n d o w i − 1 + b i t r a t e / f p s c p l x r _ s u m i − 1 + b i t s i ∗ q s c a l e i / r c e q i = ∑ i = 0 n b i t r a t e f p s ∑ i = 0 n − 1 b i t i ∗ q s c a l e i r c e q i ‘ `rateFactor=\frac{R}{\alpha}=\frac{wanted\_bits\_window_i}{cplxr\_sum_i}=\frac{wanted\_bits\_window_{i-1}+bitrate/fps}{cplxr\_sum_{i-1}+bits_i*qscale_i/rceq_i}=\frac{\sum^{n}_{i=0}\frac{bitrate}{fps}}{ \sum^{n-1}_{i=0}\frac{bit_{i}*qscale_{i}}{rceq_{i}}}` ‘rateFactor=αR=cplxr_sumiwanted_bits_windowi=cplxr_sumi−1+bitsi∗qscalei/rceqiwanted_bits_windowi−1+bitrate/fps=∑i=0n−1rceqibiti∗qscalei∑i=0nfpsbitrate‘
计算QP公式
‘ Q P = 12 + 6 ∗ log 2 α X 0.85 R = 12 + 6 ∗ log 2 b l u r r e d C o m p l e x i t y 0.85 ∗ r a t e F a c t o r ‘ ` \begin{aligned} QP&=12+6*\log_2{\frac{\alpha X}{0.85R}} \\ &=12 + 6 * \log_2{\frac{blurredComplexity}{0.85*rateFactor}} \end{aligned} ` ‘QP=12+6∗log20.85RαX=12+6∗log20.85∗rateFactorblurredComplexity‘
VBV
VBV Lookahead
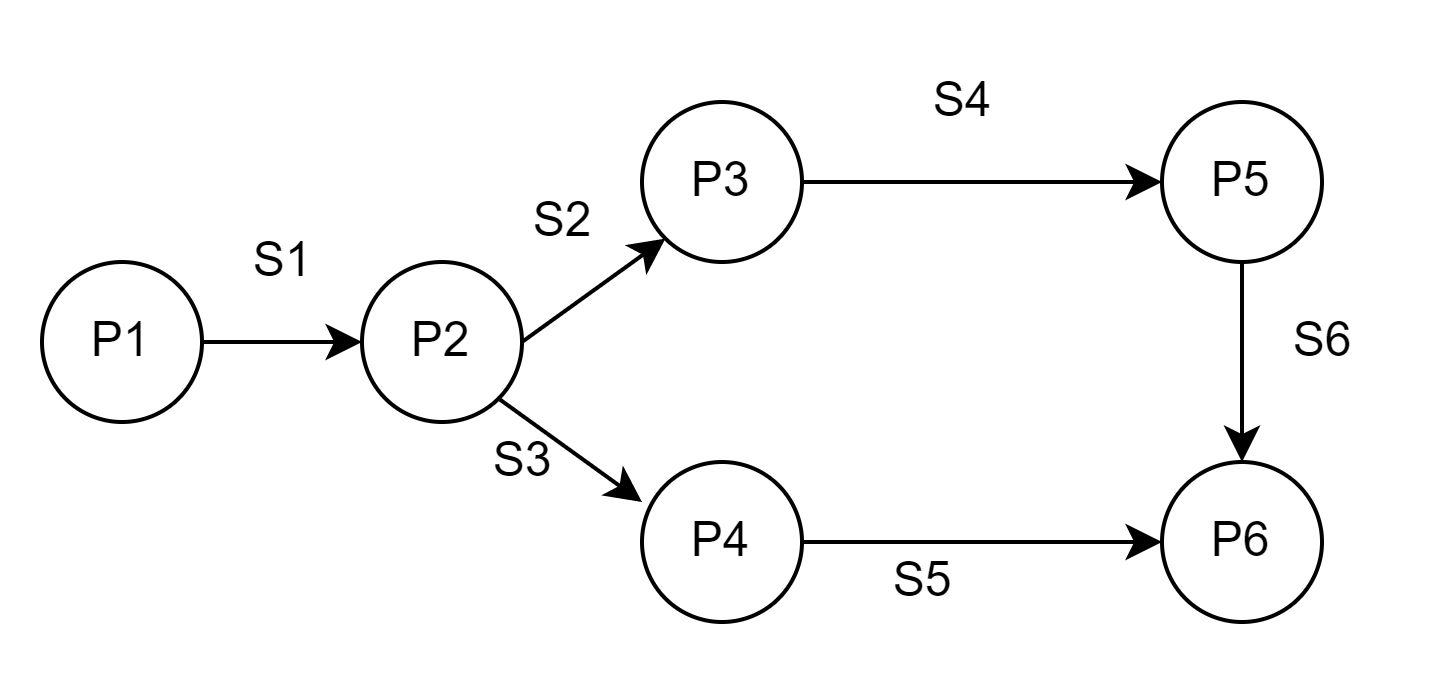
- vbv lookahead 记录编码顺序在当前帧之后且在lookahead范围内的帧的satdcost和type,记录在当前帧的
plannedSatd和plannedType数组里 - 只记录一个mini-gop,如下图所示:第0帧是I帧,mini-gop大小为1;第1~第8帧是PB帧,mini-gop大小为8
- 假设当前lookahead帧数为20
x265 VBV没有严格按照编码顺序存储信息

只有I帧的GOP
- 上图中第0帧,是I帧,mini-gop大小为1
- 先处理第一个GOP中的P帧(第8帧),然后按照顺序处理剩余B帧(第1~7帧),接着处理第二个GOP的P帧和B帧,直到处理完lookahead范围内的帧,将这些帧的信息都存储在第0帧的
plannedSatd和plannedType数组里
PB帧的GOP
- 上图中第1~第8帧就是只有PB帧的GOP,且第1~第8帧是需要输出给主编码器进行的编码的GOP
- 第9~第20帧是属于lookahead范围内的帧,当前正在处理第1~第8帧,所以,第9~第20帧还不需要输出给主编码器
- 在lookahead范围内,按照GOP顺序进行处理:先处理第一个GOP(第1~8帧),然后处理第二个GOP(第9~16帧),最后处理第17~20帧
- 先按照GOP顺序处理第一个GOP,按照顺序处理第1~7帧(第8帧是输出给主编码器进行编码的第一帧,所以不需要处理)。处理第1帧时,由于第1帧编码顺序在第8帧之后,所以,第1帧的satdcost和slicetype等信息,需要存储在第8帧的
plannedSatd和plannedType数组中,同理第1帧编码顺序在第4帧之后,所以,也需要存储在第4帧的plannedSatd和plannedType数组中,其他依次类推,第5帧编码顺序在第8、4、1、2、3帧之后,所以相关信息需要进行存储 - 接着处理第二个GOP的帧(先处理第16帧,然后处理第9~15帧),因为他们都在第一个GOP之后编码,所以,相关信息需要存储在第1~8帧里
- 最后,按照上述逻辑处理处理其他GOP的剩余帧
VBV
VBV参数初始化
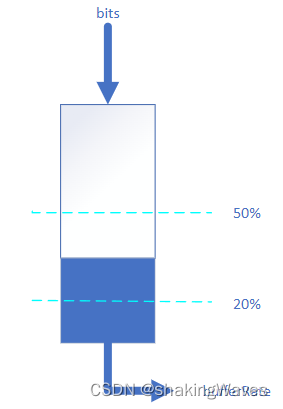
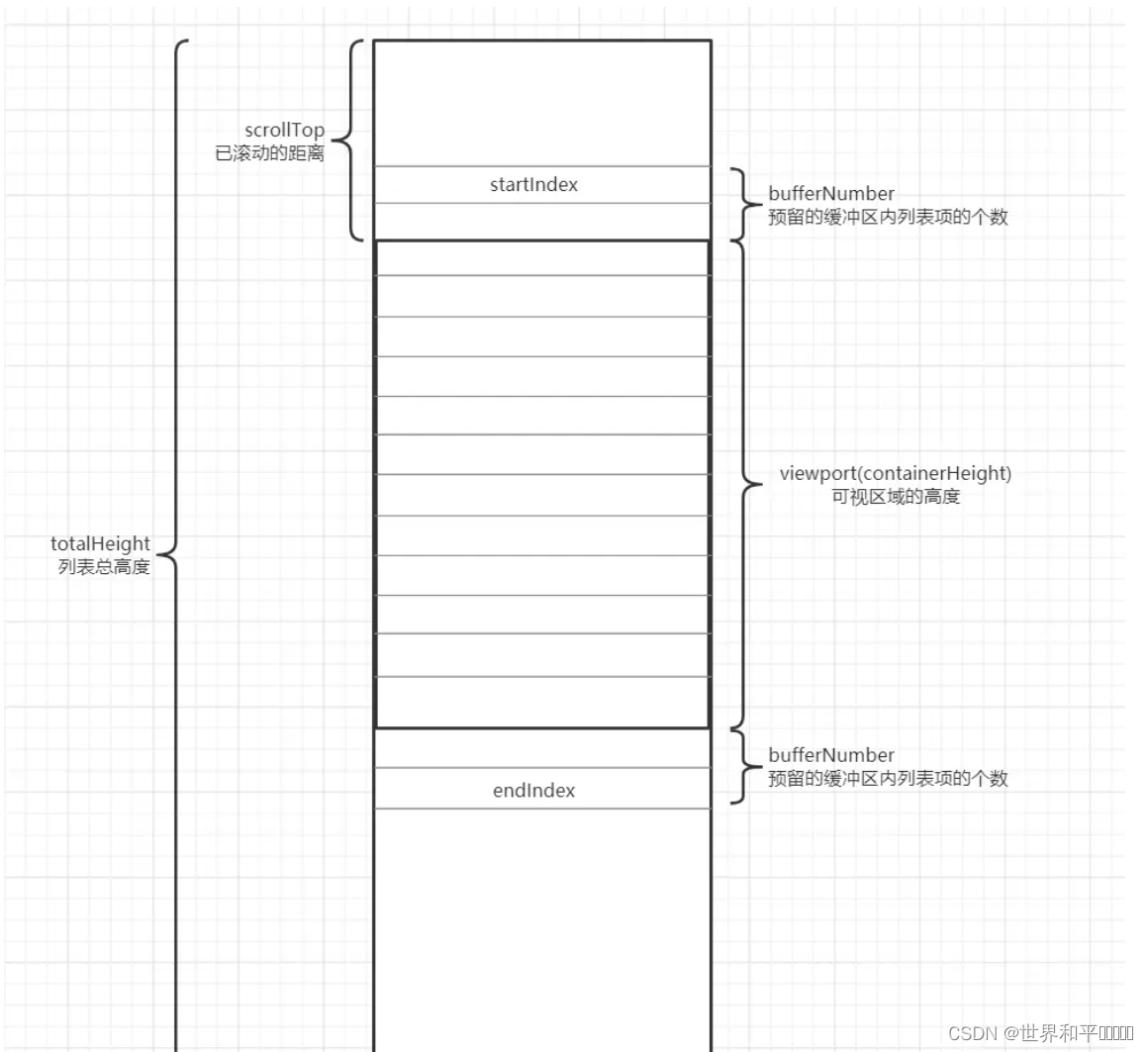
- 上图是一个vbv buffer的示意图,每帧编码完成后有bits的码流流入容器,同时也有bufferRate的码流传输出去,也就是会剩下bits-bufferRate码流
- vbv buffer的最大容量为bufferSize
- 初始化时:bufferFillFinal=bufferSize*vbvBufferInit
- vbv buffer中剩余容量 ‘ b u f f e r F i l l F i n a l − ∑ b i t s i − b u f f e r R a t e i = b u f f e r F i l l F i n a l + ∑ b u f f e r R a t e i − b i t s i ‘ `bufferFillFinal-\sum{bits_i-bufferRate_i}=bufferFillFinal+\sum{bufferRate_i-bits_i}` ‘bufferFillFinal−∑bitsi−bufferRatei=bufferFillFinal+∑bufferRatei−bitsi‘
- 要求vbv buffer中剩余容量控制在50%~80%,也就是剩余的码流要控制在20%~50%之间
假设有f个frameencoder,第X帧的buffer状态, ‘ b u f f e r F i l l X = ∑ i = 0 X − f − 1 ( b u f f e r R a t e i − b i t s i ) + ∑ i = X − f X ( b u f f e r R a t e i − m a x ( f r a m e S i z e E s t i m a t e d , f r a m e S i z e P l a n n e d ) ) ‘ `bufferFill_X=\sum^{X-f-1}_{i=0}(bufferRate_i-bits_i)+\sum^{X}_{i=X-f}(bufferRate_i-max(frameSizeEstimated,frameSizePlanned))` ‘bufferFillX=∑i=0X−f−1(bufferRatei−bitsi)+∑i=X−fX(bufferRatei−max(frameSizeEstimated,frameSizePlanned))‘
- 单线程时,RateControl::updateVbv函数里面,进行如下操作,即可以更新bufferFillFinal的值
- bufferFillFinal -= bits
- bufferFillFinal += bufferRate
- 最后将bufferFillFinal赋值给bufferFill
- 多线程时,除了调用RateControl::updateVbv函数,还需要调用Encoder::updateVbvPlan函数,对bufferFill状态进行更新,如下图所示
- 假设mini-gop为8
- 假设frameencoder为4
- 根据x265的GOP结构,编码顺序为0,8,4,1,2,3,5,6,7,如下图所示
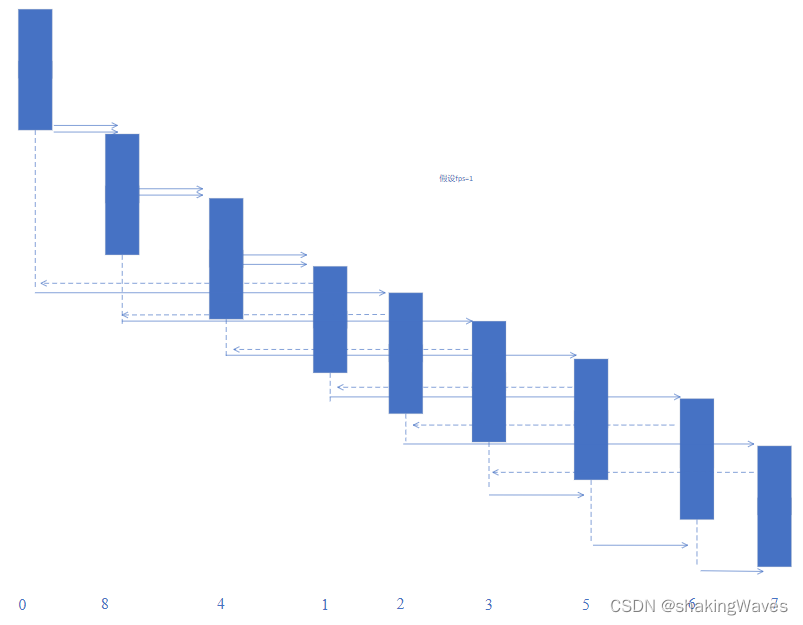
以单线程为例:使用如下命令,并在函数RateControl::updateVbv里面打印未经过运算的bufferFillFinal、bufferRate、bits以及经过计算后的bufferFillFinal,如下图所示:
--input-res 960x540 --no-info --fps 24/1 --input-depth 8 --output-depth 8 --input msub067_960x540_8bit420_24_993.yuv -p medium --keyint 32768 --open-gop --frame-threads 1 --bframes 7 --lookahead-slices 1 --pools 1 --crf 50 --vbv-maxrate 12 --vbv-bufsize 12 msub067_960x540x24x993x420p8_#2#_x265enc.265

- updateVbv是在函数rateControlEnd函数里调用
- 初始化时:bufferFillFinal=bufferSize*vbvBufferInit=12000×0.9=10800
- 前一帧的bufferFillFinal等于下一帧的未经过计算的bufferFillFinal
- bufferFillFinal最终赋值给bufferFill
帧级VBV
预测模型
‘ 根据上面假设,可以得到: q ∝ v a r b i t s 如果按照一阶线性模型,可以得到 b i t s ∗ q = v a r ∗ c o e f f + o f f s e t 迭代更新: c o e f f i + 1 = b i t s ∗ q − o f f s e t i v a r o f f s e t i + 1 = b i t s ∗ q − c o e f f i + 1 ∗ v a r 为了平滑 c o e f f 和 o f f s e t , c o e f f = ∑ i = 0 n + 1 d e c a y n + 1 − i ∗ c o e f f i o f f s e t = ∑ i = 0 n + 1 d e c a y n + 1 − i ∗ o f f s e t i c o u n t = ∑ i = 0 n + 1 d e c a y n + 1 − i ∗ c o u n t i 最终 b i t s = c o e f f ∗ v a r + o f f s e t q ∗ c o u n t ‘ ` \begin{aligned} &根据上面假设,可以得到:q\propto\frac{var}{bits} \\ &如果按照一阶线性模型,可以得到 bits*q=var*coeff+offset \\ &迭代更新:coeff_{i+1}=\frac{bits*q-offset_{i}}{var}\\ &offset_{i+1}=bits*q-coeff_{i+1}*var\\ & 为了平滑coeff和offset, \\ & coeff=\sum^{n+1}_{i=0}decay^{n+1-i}*coeff_{i}\\ & offset=\sum^{n+1}_{i=0}decay^{n+1-i}*offset_{i}\\ & count=\sum^{n+1}_{i=0}decay^{n+1-i}*count_{i}\\ & 最终bits=\frac{coeff*var+offset}{q*count} \\ \end{aligned} ` ‘根据上面假设,可以得到:q∝bitsvar如果按照一阶线性模型,可以得到bits∗q=var∗coeff+offset迭代更新:coeffi+1=varbits∗q−offsetioffseti+1=bits∗q−coeffi+1∗var为了平滑coeff和offset,coeff=i=0∑n+1decayn+1−i∗coeffioffset=i=0∑n+1decayn+1−i∗offseticount=i=0∑n+1decayn+1−i∗counti最终bits=q∗countcoeff∗var+offset‘
I/P帧
帧级VBV主要通过clipQscale函数进行调整。主要使用三个信息调整qscale
-
码控计算得到的原始qscale
-
利用VBV Lookahead中当前帧存储的
plannedSatd和plannedType信息(最多1秒) -
使用上面的预测模型计算后续最多1秒的帧的比特
利用以上信息可以得到当前buffer的剩余预算bufferFillCur,比较bufferFillCur和targetFill的大小,调整qscale的大小
- 至少保证剩余预算bufferFillCur至少50%可用,否则说明编码产生的比特太多,需要调大qscale
- 保证剩余预算bufferFillCur大于80%,否则说明编码产生的比特太少,需要调小qscale
‘ b u f f e r F i l l C u r = b u f f e r F i l l + ∑ i = 0 m i n ( r c l o o k a h e a d , f p s ) ( b u f f e r R a t e i − b i t s i ) t a r g e t F i l l 50 = M I N ( b u f f e r F i l l + t o t a l D u r a t i o n ∗ v b v M a x R a t e ∗ 0.5 , b u f f e r S i z e ∗ ( 1 − m i n B u f f e r F i l l ∗ f i n a l D u r ) ) t a r g e t F i l l 80 = c l i p 3 ( b u f f e r S i z e ∗ ( 1 − m a x B u f f e r F i l l ∗ f i n a l D u r ) , b u f f e r S i z e , b u f f e r F i l l − t o t a l D u r a t i o n ∗ v b v M a x R a t e ∗ 0.5 ) q = { q ∗ 1.01 , b u f f e r F i l l C u r < t a r g e t F i l l 50 q / 1.01 , b u f f e r F i l l C u r > t a r g e t F i l l 80 ‘ ` \begin{aligned} &bufferFillCur=bufferFill+\sum^{min(rclookahead,fps)}_{i=0}(bufferRate_i-bits_i) \\ &targetFill_{50}=MIN(bufferFill + totalDuration * vbvMaxRate * 0.5, bufferSize * (1 - minBufferFill * finalDur)) \\ &targetFill_{80}=clip3(bufferSize * (1 - maxBufferFill * finalDur), bufferSize, bufferFill - totalDuration * vbvMaxRate * 0.5) \\ &q= \begin{cases} q * 1.01, bufferFillCur<targetFill_{50} \\ q/1.01, bufferFillCur>targetFill_{80} \\ \end{cases} \\ \end{aligned} ` ‘bufferFillCur=bufferFill+i=0∑min(rclookahead,fps)(bufferRatei−bitsi)targetFill50=MIN(bufferFill+totalDuration∗vbvMaxRate∗0.5,bufferSize∗(1−minBufferFill∗finalDur))targetFill80=clip3(bufferSize∗(1−maxBufferFill∗finalDur),bufferSize,bufferFill−totalDuration∗vbvMaxRate∗0.5)q={q∗1.01,bufferFillCur<targetFill50q/1.01,bufferFillCur>targetFill80‘
- 剩余bufferFillCur的容量不能低于 ‘ t a r g e t F i l l 50 ‘ `targetFill_{50}` ‘targetFill50‘,否则说明编码数据太多了,需要增大QP。至少要保证vbv buffer里50%的空间剩余。如果上一帧在真正编码之后,生成的码流很大,剩余空间bufferFill很小,导致 ‘ b u f f e r F i l l + t o t a l D u r a t i o n ∗ v b v M a x R a t e ∗ 0.5 < b u f f e r S i z e ∗ ( 1 − m i n B u f f e r F i l l ∗ f i n a l D u r ) ‘ `bufferFill + totalDuration * vbvMaxRate * 0.5< bufferSize * (1 - minBufferFill * finalDur)` ‘bufferFill+totalDuration∗vbvMaxRate∗0.5<bufferSize∗(1−minBufferFill∗finalDur)‘,如果让bufferFillCurr大于50%的bufferSize,可能又会造成码流突然变小,从而导致码流波动过大,质量劣化,所以,此时只需要满足 ‘ b u f f e r F i l l + t o t a l D u r a t i o n ∗ v b v M a x R a t e ∗ 0.5 ‘ `bufferFill + totalDuration * vbvMaxRate * 0.5` ‘bufferFill+totalDuration∗vbvMaxRate∗0.5‘即可
- 剩余bufferFillCur的容量不能大于 ‘ t a r g e t F i l l 80 ‘ `targetFill_{80}` ‘targetFill80‘,否则说明编码数据太少了,需要调小QP。若上一帧编码完成之后,bufferFill大于了80%,而且bufferFill - totalDuration * vbvMaxRate * 0.5也大于80%的bufferSize,那么当前帧在编码的时候,需要控制bufferFillCur不能减少的太快,防止质量劣化太严重,bufferFillCur控制在bufferFill - totalDuration * vbvMaxRate * 0.5,即可
B帧VBV
根据向后参考帧的平均QP,计算当前帧的QP,然后映射为qscale值,并预估bits
- pbFactor和ipFactor用来调节QP值
行级VBV
行比特估计predictRowsSizeSum
predictRowsSizeSum函数计算当前帧已编码端比特和未编码的预测比特之和
‘ a c c F r a m e B i t s = ∑ r o w = 0 m a x R o w s e n c o d e d B i t s S o F a r r o w + t o t a l S a t d B i t s r o w t o t a l S a t d B i t s r o w = { p r e d _ s + p r e d T o t a l 2 , 当前帧和参考帧都为 P 帧, q s c a l e ≥ r e f Q S c a l e , 当前帧未编码的 s a t d C o s t F o r P e n d i n g C u s 和参考帧未编码的 r e f R o w S a t d C o s t 差异较小 p r e d _ s + p r e d _ i n t r a , 当前帧是 P 帧, q S c a l e ≤ r e f Q S c a l e p r e d _ s , 其他 ( I 帧, B 帧,以及 P 帧其他情况 ) ‘ ` \begin{aligned} & accFrameBits= \sum^{maxRows}_{row=0}encodedBitsSoFar_{row}+totalSatdBits_{row} \\ &totalSatdBits_{row}= \begin{cases} \frac{pred\_s+predTotal}{2},当前帧和参考帧都为P帧,qscale \geq refQScale, 当前帧未编码的satdCostForPendingCus和参考帧未编码的refRowSatdCost差异较小 \\ pred\_s + pred\_intra, 当前帧是P帧,qScale \leq refQScale \\ pred\_s, 其他(I帧,B帧,以及P帧其他情况) \\ \end{cases} \\ \end{aligned} ` ‘accFrameBits=row=0∑maxRowsencodedBitsSoFarrow+totalSatdBitsrowtotalSatdBitsrow=⎩ ⎨ ⎧2pred_s+predTotal,当前帧和参考帧都为P帧,qscale≥refQScale,当前帧未编码的satdCostForPendingCus和参考帧未编码的refRowSatdCost差异较小pred_s+pred_intra,当前帧是P帧,qScale≤refQScalepred_s,其他(I帧,B帧,以及P帧其他情况)‘
- pred_s:根据上面提及的预测模型,利用未编码CTU的SATD值估计出的比特
qpVbv调整
- 满足如下条件,增大qpVbv
- qpVbv < qpMax
- 当前帧的估计比特accFrameBits > frameSizePlanned + rcTol
- bufferFill - accFrameBits < bufferLeftPlanned * 0.5
- 当前估计bits大于实际占用bits
- 占用bits过大
- 满足如下条件,减少qpVbv
- qpVbv > qpMin
- 当前qpVbv大
- 预估比特太小
- 调整之后再调整一下qpVbv防止下溢
VBV更新
编码完成之后更新bufferFillFinal
reference
[1] Asymptotically efficient quantizing.pdf
[2] Lagrange multiplier selection in hybrid video coder control.pdf