对传递函数的零极点、频率响应、稳定性的理解

零极点

从传递函数求零极点

令传递函数分子为0求出零点，令分母为0求出零点。

频率响应

单极点系统的频率响应

$Av=A{v}_{d}c\ast (1/(1+sRC))$，系统的极点是$p=-1/RC$。零极点是用于判断系统的稳定性的，传递函数的模值随s（频率）的变化便是频率响应的曲线。

在频率响应的曲线中，当$w=|p|=1/RC$时，传递函数的模值$|1/(1+sRC)|$变为$1/sqrt(2)$，对应AV(dB)减少3dB时。

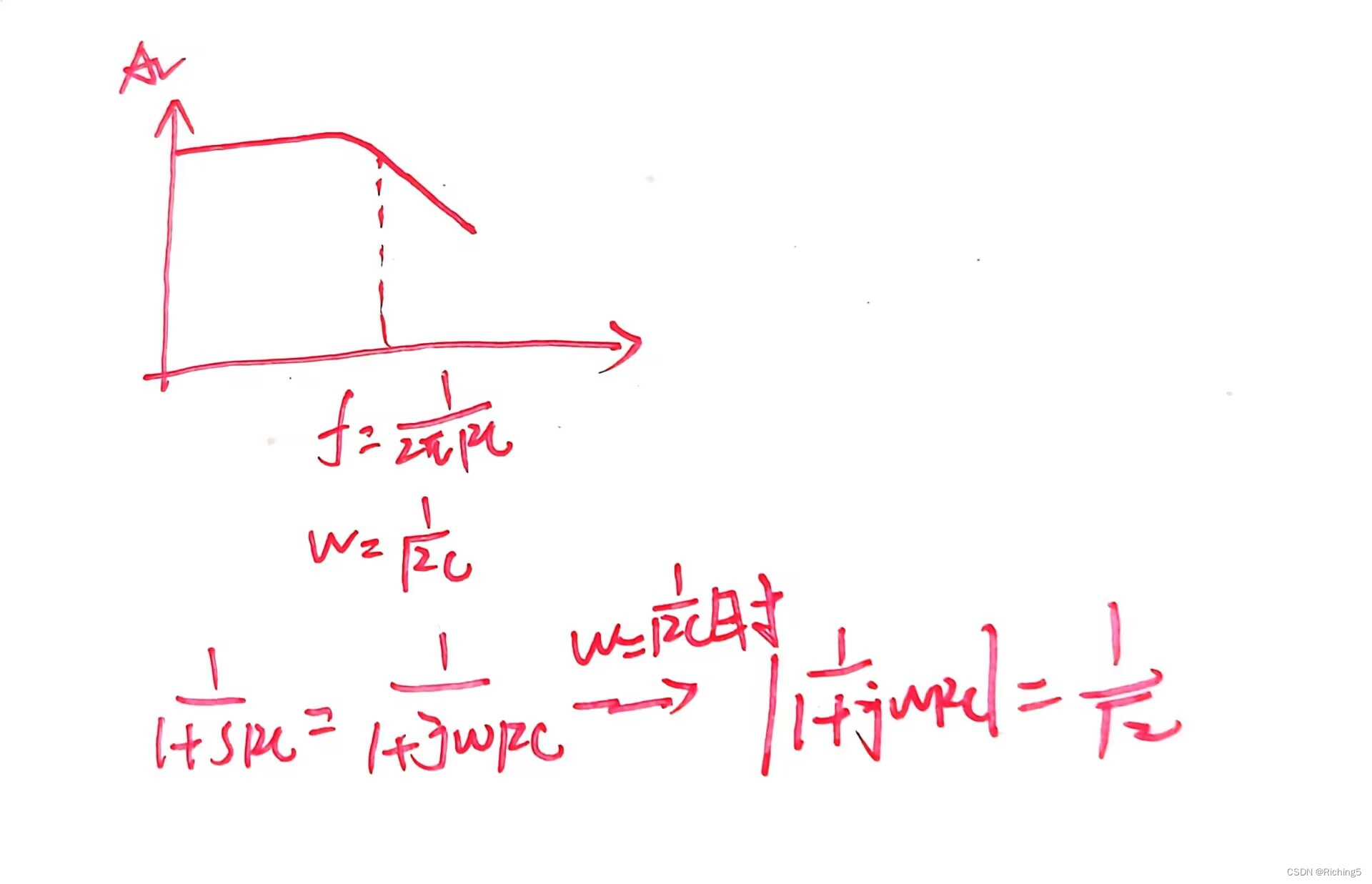
零极点对频率响应曲线的影响

零点和极点对频率响应的影响 - 模拟集成电路之频率响应分析零极点 - 电子发烧友网

• 当频率远小于某零点/极点的模时，该零点/极点对频率响应的影响可以忽略。
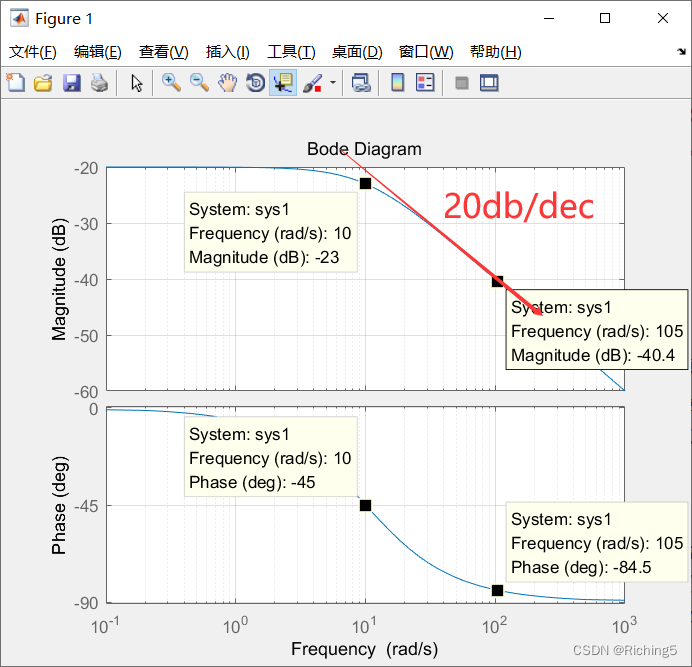
• 当频率接近某极点的模时，该极点的效果渐渐体现。当频率远大于该极点时，该极点使得频率响应的幅度以20dB/dec的速度衰减，而相位相对DC产生-π/2的变化。

例如下图为传递函数为$H(s)=1/(s+10)$的频率响应和相位图：

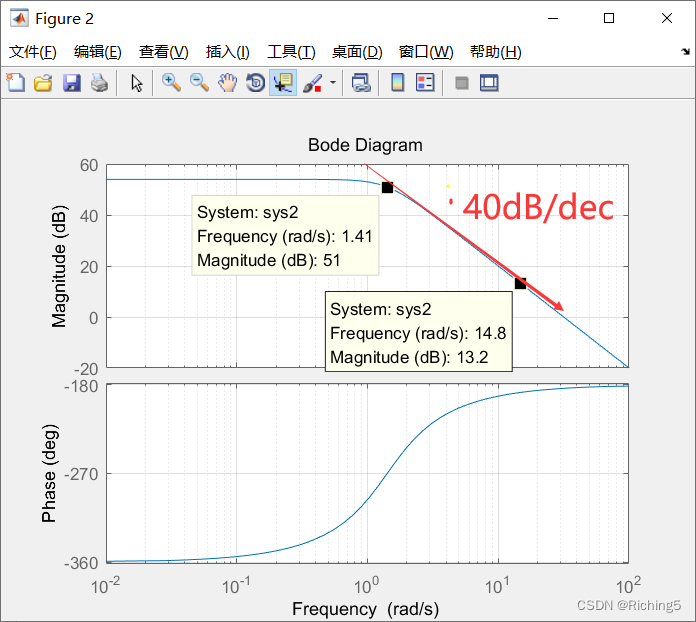
• 共轭极点是一种特殊的极点，它们总是成对出现且共轭极点对的模都相等，因此当频率远大于一对共轭极点的模的时候，该共轭极点对会使频率响应的幅度以40dB/dec的速度衰减，而相位相对DC产生-π的变化。而在频率接近共轭极点对的模的时候，频率响应曲线的变化取决于共轭极点对的位置（详见原文）。

例如下图为传递函数为$H(s)=1000/(s^2-2s+2)$的频率响应和相位图：

• 当频率接近某零点的模时，该零点的效果渐渐体现。当频率远大于该零点时，该零点使得频率响应的幅度以20dB/dec的速度增加。而相位相对DC产生π/2（当零点在左半平面）或-π/2（当零点在右半平面）的变化。

例如下图为传递函数为$H(s)=1000(s-10)$的频率响应和相位图：

• 频率响应的总体幅度/相位取决于所有零点和极点对幅度/相位的贡献。

matlab构造传递函数和绘制波特图

Matlab仿真001-传递函数_传递函数 matlab_k_c_c_的博客-CSDN博客

所用到的matlab函数

多个角度理解极点与零点，电容充放电的联系

【模拟IC学习】多个角度理解极点与零点，电容充放电的联系

时域上看极点的作用

模拟电路基础之频率响应（一）极点的物理意义

极点时是从一个结点看进去所有电阻和电容的乘积，这里以RC电路为例说明极点的作用，或者说RC对于不同信号频率的作用。

首先需要知道Vout是怎么随着Vin变化的：从电流方向来看，当Vin大于Vout时，电流流向C为充电，Vout会增加，直到Vout=Vin；反之为放电，Vout会减少直到Vout=Vin。这里Vin是主动变化，Vout是被动跟随Vin。而且充放电是需要时间的，这与Fin和C的相对大小有关，Fin越大，C越小充电越快，Vout跟随Vin越好。

还需要知道相位差和时延的关系：

1. 根据波特图，当输入信号Vin的频率为1/2πRC时，Vout的相位会滞后45°，幅值会变为原来的$1/\sqrt{2}$。

理论上时域会相差8/T。在仿真中设置R=1K，C=1p，fin=159Mhz，Tin=6.28ns，amplitude=1，所以输出滞后输入0.785ns，幅值变为0.707，符合波特图：

从时域上理解为，对C充放电是需要时间的，C越大充放电越慢，当Vin>Vout时，C在充电电流下，Vout逐渐上升，但还没上升到和Vin幅度一样，Vin已经下降到Vin=Vout，导致Vout不能充电到Vin_max就开始放电了，当然放电也需要时间，所以Vout还没放电到Vin_min时就结束放电开始充电了。综上我们看到Vout不仅滞后Vin，并且幅度也小了。

1. fin<<1/2πRC时，或者说C很小时，或者说是直流输入时，极点的影响就很小：

这是因为C很小，充放电很快，或者说Vin变化很慢，Vout很容易跟随。

1. 当但fin>>1/2πRC时，或者说C很大时，极点的影响就很大，但一个极点最多只能产生90°的相移：

那为什么最大只有90°相移呢？随着fin的增加，或者说C很大，充放电极其慢。可以看下图固定输入频率，不断增加C。随着C增加下Vout=Vin的交点越靠近Vin=0。那最坏的极限情况是，当Vin=0时，Vout才充电到最大随后开始放电，此时Vout的最大值与Vin的最大值时间上相差T/4，对应相移90°。而最坏时Vout的最大接近为0，这就像往海里扔一块石子，对海平面的影响微乎其微。

零点的直接理解

零点是由于前馈通路造成的。本来通路中有一个极点，会造成相位延迟和增益下降。但是如果在输入与输出之间有一条前馈通路，如下图中的Cz所示，可以让信号不通过极点所在的结点而是通过前馈通路直接到达，那么极点所造成的影响就会被部分抵消。极限情况就是信号完全通过通路到达输出，把极点所带来的相位延迟全部抵消。因此可以知道零点最大可以带来90°的相位超前（但是这儿的超前不是说输出超前于输入，只是可以把极点带来的相位延迟进行一定的补偿）。

下图传递函数的极点低于零点，所以极点的效果会先出现——系统会先出现相位延迟。随着频率升高，信号会更多的从Cz通过，补偿极点带来的相位延迟。最终频率足够高时，信号完全从Cz通过，此时电路等效为Cz和C的分压电路，此时极点与零点对相位影响完全抵消。

（注意图中P和Z是极点频率，即极点的模值，所以是正值；如果极点频率单位为Hz，还需要除以2π）

仿真一下这个电路，设置Cz=0.1pF，C=1pF，R=1k，极点频率=156Mhz，零点频率=1560Mhz。

当Fin=156Mhz时，可以看到主要是极点起作用，延时和幅度衰减和前文分析一致。

当Fin=1560Mhz，此时相位差回到45°，还是滞后T/4（注意这里Fin变为前面的十倍，周期为1/10），幅值为原来的1/6。

当Fin=15600Mhz，此时相位差为0，幅值为原来的0.09，是电容分压产生。

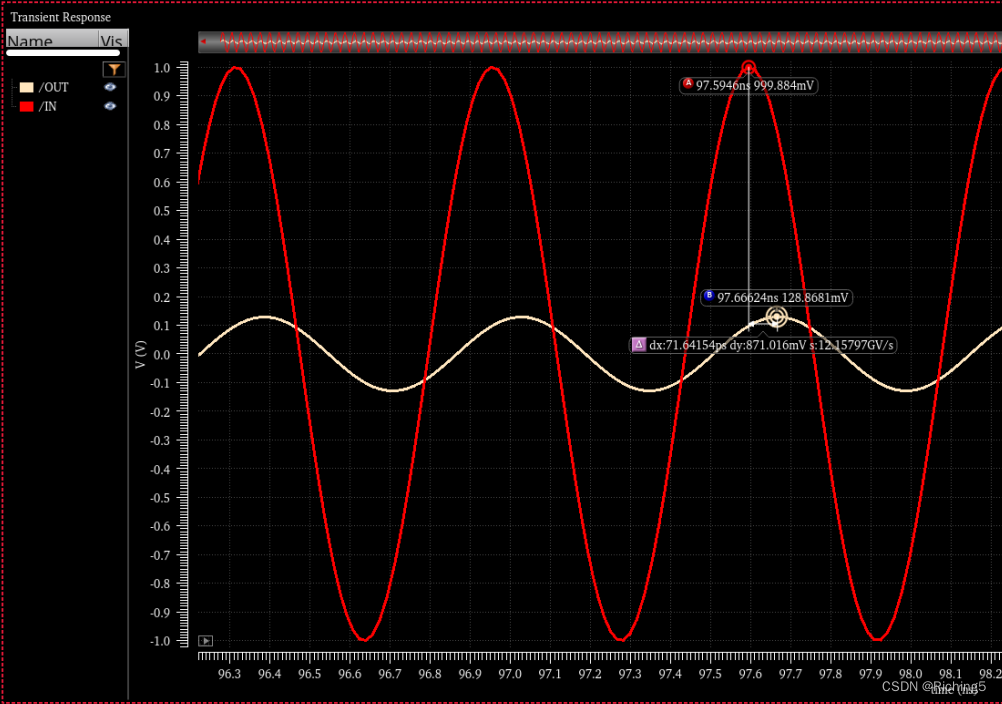
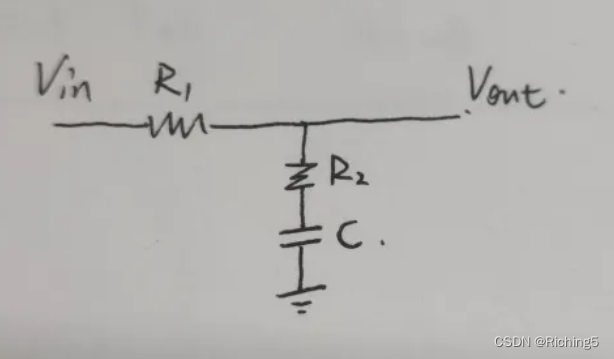
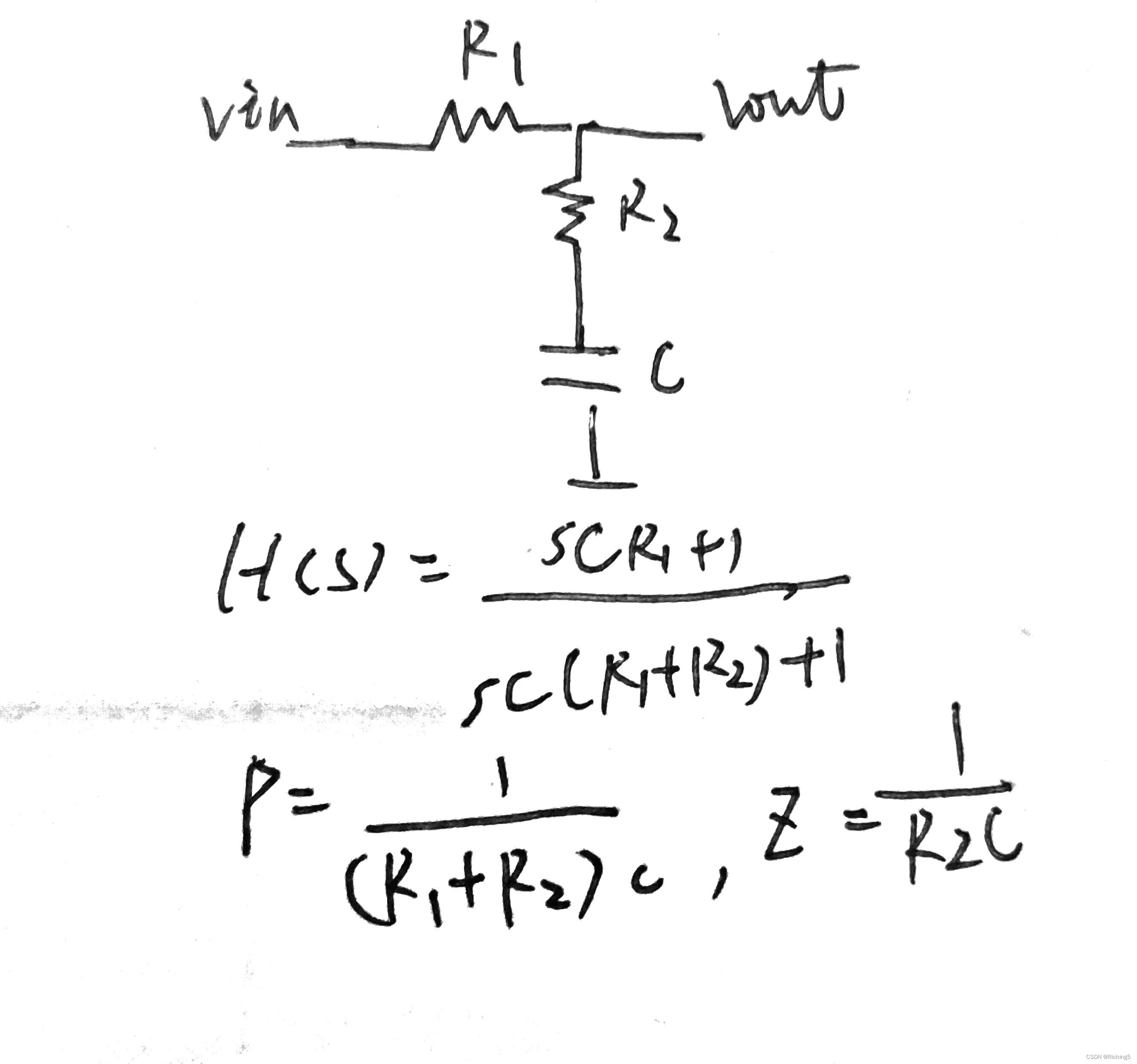
输出节点串联R+C会引入零点

信号传递过程中，一样要给电容充电，所以有相位延迟和幅度降低，因此会产生一个极点。给电容充电过程中电流要流过电阻，因此电阻两端要产生压差，一定程度上增加了输出端口的电压，降低了延迟并且阻碍了幅度降低，因此体现为一个零点。

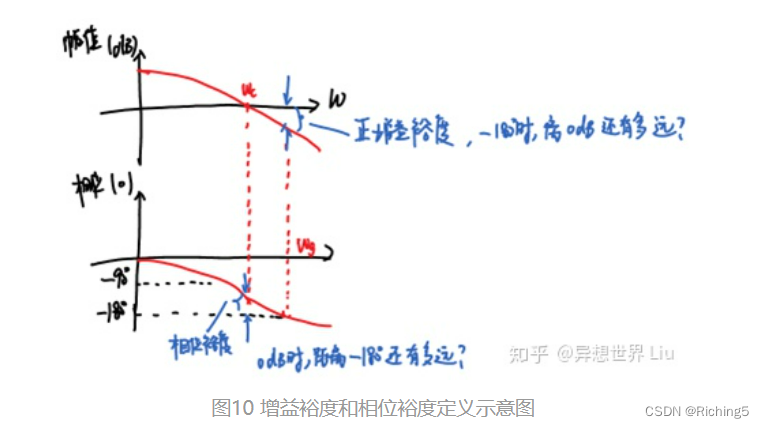
相位裕度PM

定义为开环增益为0dB时，PM=180°+φ(w)，φ(w)是频率为w时的相位角，代表增益0dB时，相位角离-180°的距离。越正越好。

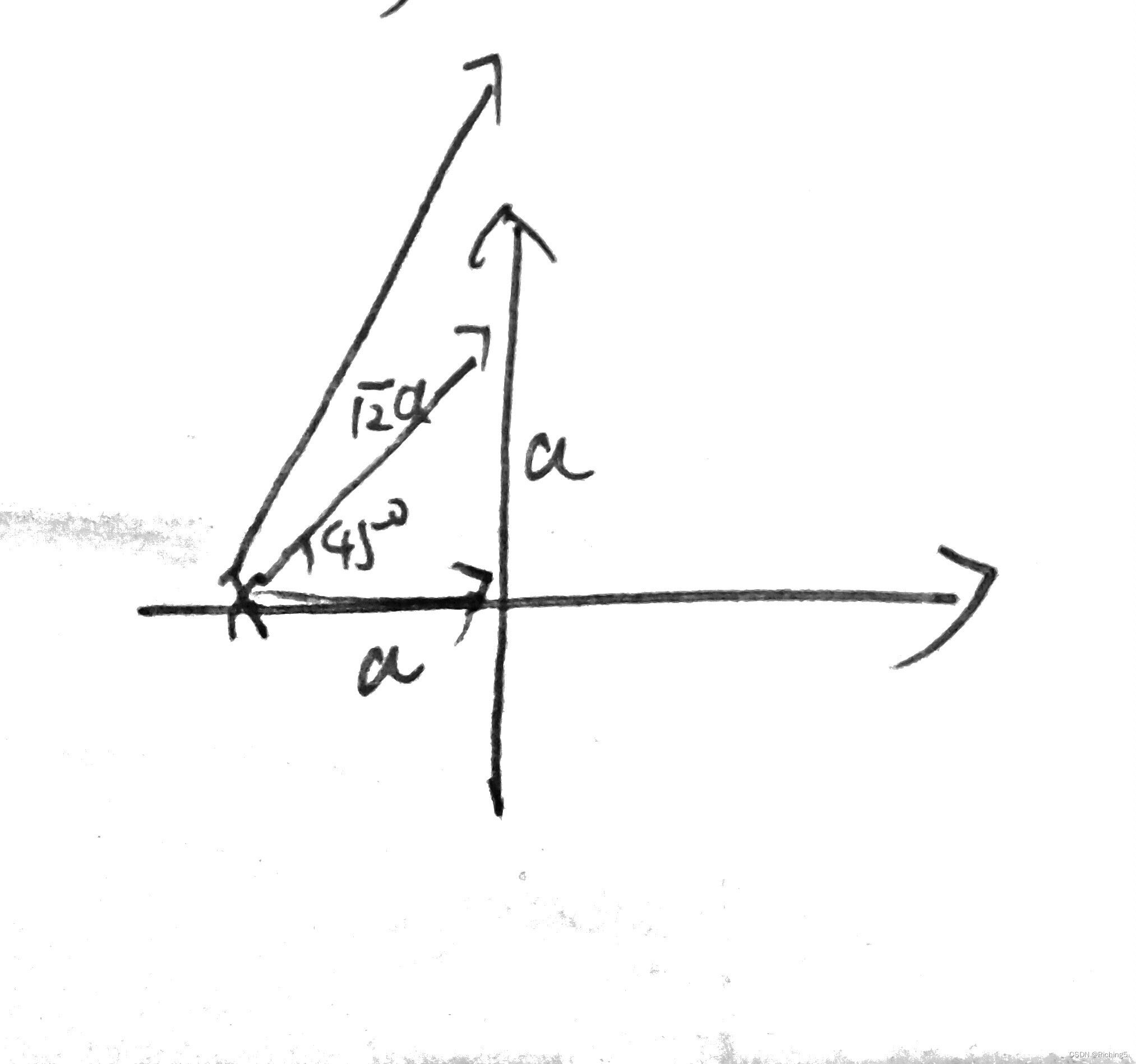
零极点对稳定性的影响

在普通的电路里，极点都是左半平面的，即通过s参数算出来是负的，因为右半平面的极点在时域会使信号不断发散。零点可以在左半平面，也可以在右半平面。算出来是负的就在左平面，算出来是正的就在右平面。

用矢量作图法看极点的影响：当w=0时，即直流增益等于极点到原点的距离a的倒数，随着频率w的增加，距离逐渐增加，增益逐渐减少，当矢量与正半轴的夹角为45°时，即一个极点贡献的相位角是0-45°=-45°，对应相位为-45°，距离的倒数为$a/\sqrt{2}$，对应增益减少3dB，都对应前面的分析。零点也可以做类似分析。

那当有反馈的系统存在右半平面的零点为什么会不稳定？

根据矢量分析法，右半平面的实零点贡献的相位是负的。因为当w=z的虚部时，贡献的相位是π+π=0°，当f增加时，最终贡献的相位是π+π/2,=-pi/2。

本来电路中的常存在的左半面极点就会贡献负的相位角，如果还存在右半面的零点，更容易导致增益为0dB时，相位裕度不满足要求。与此同时，左半平面零点贡献的相位是正的，更有利于相位裕度。

矢量作图法分析系统的幅频、相频曲线

可以通过矢量作图法分析系统的幅频、相频曲线。

首先将传输函数化为零极点的标准形式，在复平面上画下零极点的位置。

频率变化时，也就是扫描虚轴，从负无穷到正无穷。

对于幅频特性曲线，扫描虚轴，求出每个零极点到虚轴上某点的距离的模值，按下面公式相比乘K得到幅频特性曲线；对于相频特性曲线，扫描虚轴，求出每个零极点指向虚轴上某点的矢量与正实轴形成的夹角，将零点的夹角求和减去极点的夹角和。注意：对于右零点，或者右极点算相位贡献时，画矢量图，考虑负号的影响，需要加上一个附加相位pi