1、题目描述

On the Internet, machines (nodes) are richly interconnected, and many paths may exist between a given pair of nodes. The total message-carrying capacity (bandwidth) between two given nodes is the maximal amount of data per unit time that can be transmitted from one node to the other. Using a technique called packet switching; this data can be transmitted along several paths at the same time.

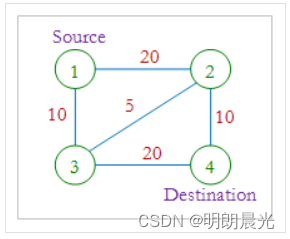
For example, the figure shows a network with four nodes (shown as circles), with a total of five connections among them. Every connection is labeled with a bandwidth that represents its data-carrying capacity per unit time.

In our example, the bandwidth between node 1 and node 4 is 25, which might be thought of as the sum of the bandwidths 10 along the path 1-2-4, 10 along the path 1-3-4, and 5 along the path 1-2-3-4. No other combination of paths between nodes 1 and 4 provides a larger bandwidth.

You must write a program that computes the bandwidth between two given nodes in a network, given the individual bandwidths of all the connections in the network. In this problem, assume that the bandwidth of a connection is always the same in both directions (which is not necessarily true in the real world).

在这里插入图片描述
Input
Input starts with an integer T (≤ 30), denoting the number of test cases.

Every description starts with a line containing an integer n (2 ≤ n ≤ 100), which is the number of nodes in the network. The nodes are numbered from 1 to n. The next line contains three numbers s, t, and c. The numbers s and t are the source and destination nodes, and the number c (c ≤ 5000, s ≠ t) is the total number of connections in the network. Following this are c lines describing the connections. Each of these lines contains three integers: the first two are the numbers of the connected nodes, and the third number is the bandwidth of the connection. The bandwidth is a non-negative number not greater than 1000.

There might be more than one connection between a pair of nodes, but a node cannot be connected to itself. All connections are bi-directional, i.e. data can be transmitted in both directions along a connection, but the sum of the amount of data transmitted in both directions must be less than the bandwidth.

Output
For each case of input, print the case number and the total bandwidth between the source node s and the destination node t.

Sample
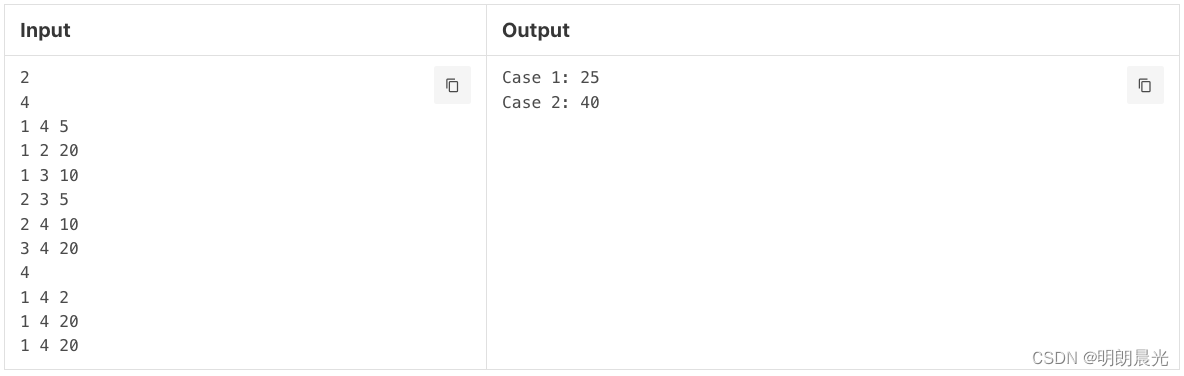
在这里插入图片描述
原题链接：Internet Bandwidth

2、思路分析

最大网络流问题，一定要指明每条线路的承载量，一定要指明源点和目标点。
在这里插入图片描述
该有向图中，从A到D的整个流最大是130。

dinic算法的核心在于负反馈，补反向边的代价，解决的是成环节点的问题。

举个例子：
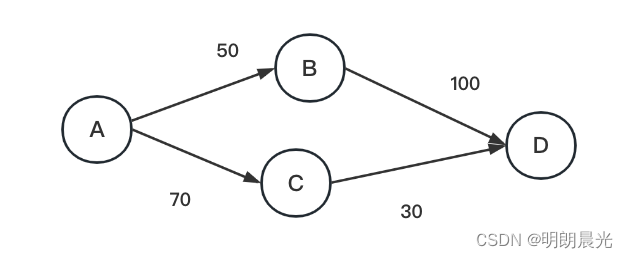
在这里插入图片描述
两种走法：

A->B->D，最小边50，所以每条边减50，然后增加反向的50的边
A->C->D，最小边30，所以每条边减30，然后增加反向的30的边

即：
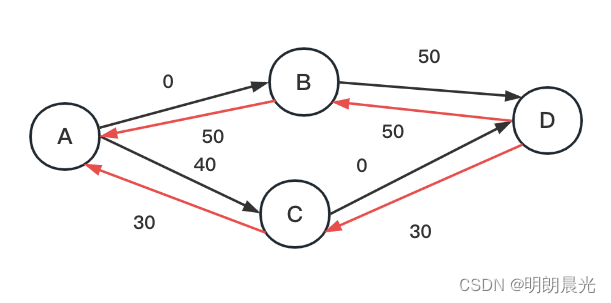
在这里插入图片描述
Dinic算法还有两个优化的点。

第一个优化的点——建立高度数组：先广度优先遍历，确定每个节点所在的层数，然后使用深度优先遍历，如果某个节点有多条路可以选择，选择节点所在层数比当前节点层数大的路径。

例如：
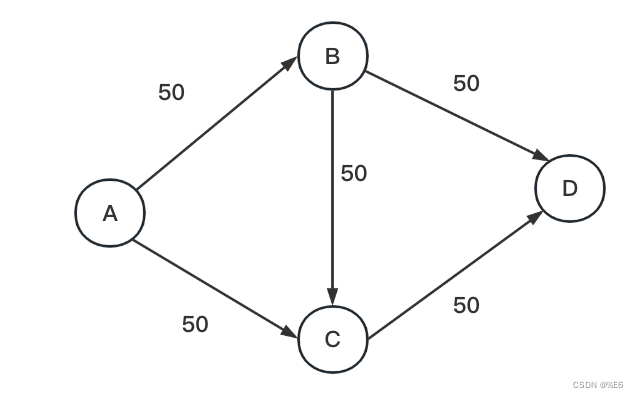
在这里插入图片描述
从 A 出发，进行广度优先遍历，则：

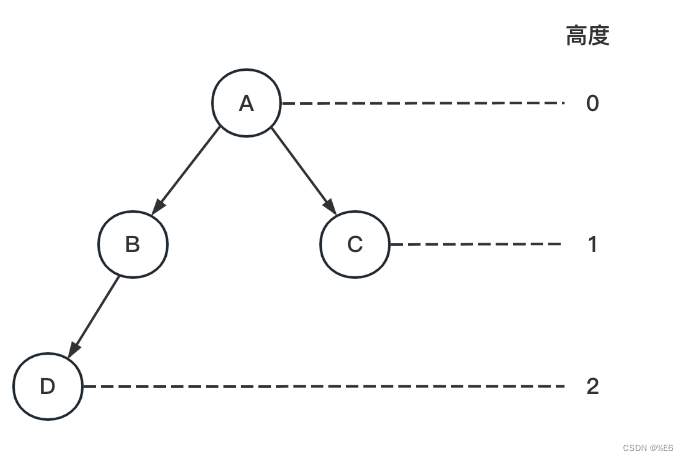
建立一个高度数组，记录每个点所在的层数：

层数数组：[0, 1, 1, 2]
节点： 	 A 	B  C  D

然后从A出发往前走到时候，只选择层数变大的路：A->B，因为A是0层，B是1层；B不能到C，因为二者层数相同，按照这种规则，所以路线就是A->B->D 和 A->C->D。

总结来说，就是先建立起高度数组，然后DFS，这样可以避免来回走的问题。

第二个优化的点——建立一个数组，记录每个节点经过的支路。
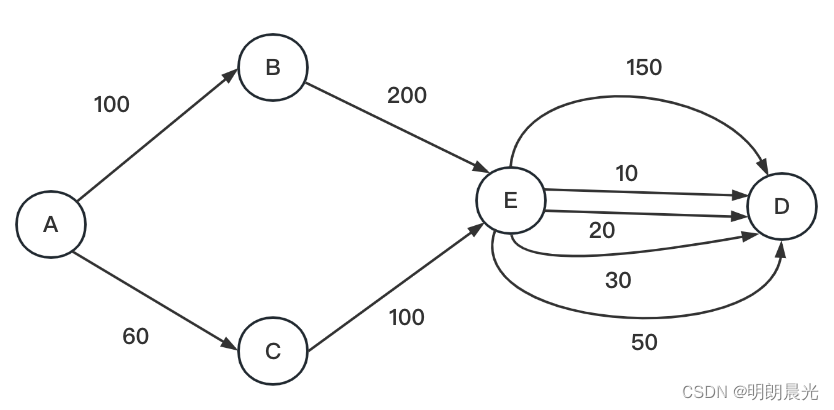
在这里插入图片描述
A->B，传输100，B->E，传输100，此时到E这里要往D传输100，E先选择10这条路，该路径使用了就变成0，还剩100-10 = 90要传输，接着选择20，该路径也变成0；还剩90-20=70要传输，接着选择30，该路径也变成0；还剩70-30=40要传输，接着选择50这条路，只需要占用40，该路径变成10。此时100的任务传输完成。
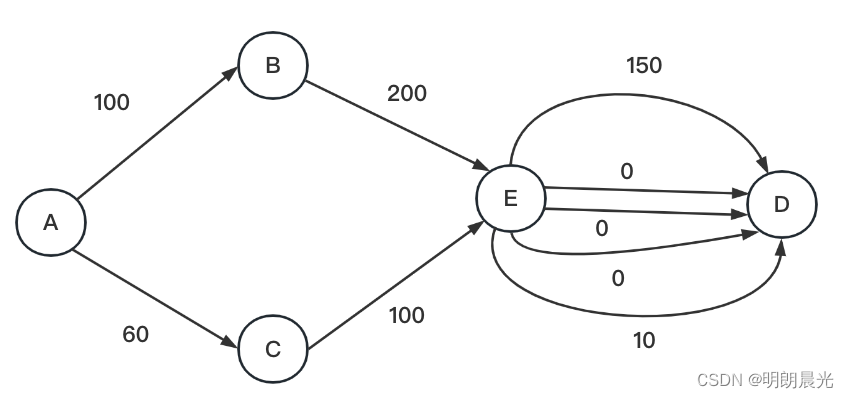
在这里插入图片描述
若此时A->C，传输60，C->E传输60，此时E要往D传输60，而可用的路径只有10和150这两条，其他路径不再考虑。

3、代码实现

// 本题测试链接:
// https://lightoj.com/problem/internet-bandwidth
// 这是一道DinicAlgorithm算法的题
// 把如下代码粘贴进网页所提供的java编译器环境中
// 不需要修改任何内容可以直接通过
// 请看网页上的题目描述并结合main函数的写法去了解这个模板的用法
// 请务必参考如下代码中关于输入、输出的处理
// 这是输入输出处理效率很高的写法
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;

public class DinicAlgorithm {

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StreamTokenizer in = new StreamTokenizer(br);
		PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
		while (in.nextToken() != StreamTokenizer.TT_EOF) {
			int cases = (int) in.nval;
			for (int i = 1; i <= cases; i++) {
				in.nextToken();
				int n = (int) in.nval;
				in.nextToken();
				int s = (int) in.nval;
				in.nextToken();
				int t = (int) in.nval;
				in.nextToken();
				int m = (int) in.nval;
				Dinic dinic = new Dinic(n);
				for (int j = 0; j < m; j++) {
					in.nextToken();
					int from = (int) in.nval;
					in.nextToken();
					int to = (int) in.nval;
					in.nextToken();
					int weight = (int) in.nval;
					//因为是无向图，所以要加4条边，而addEdge一次加两条，所以调用两次addEdge
					dinic.addEdge(from, to, weight);
					dinic.addEdge(to, from, weight);
				}
				int ans = dinic.maxFlow(s, t);
				out.println("Case " + i + ": " + ans);
				out.flush();
			}
		}
	}

	public static class Edge { //有向边
		public int from; //点的编号，边的起点
		public int to; //点的编号，边的终点
		public int available; //边的剩余可用承载量

		public Edge(int a, int b, int c) {
			from = a;
			to = b;
			available = c;
		}
	}

	public static class Dinic {
		//点的数量
		private int N; 
		
		//edges记录所有的边，包括反向边
		//假设有第0条边 (1,3,20), 第1条边(3,2,10)
		//根据第0条边生成 (1,3,20) 和 (3,1,0) , 根据第1条边生成 (3,2,10) 和 (2,3,0)，反向边的available记录的就是使用的量
		//将生成的边记录到edges中：[(1,3,20), (3,1,0), (3,2,10), (2,3,0)]
		private ArrayList<Edge> edges; 
		
		//nexts记录每个点和哪些边有关：
		//0 : {}  表示和点0相关的边没有
		//1 : {0}  表示和点1相关的点是edges数组中的第0条边，记录的是边的编号
		//2 : {3}  表示和点2相关的点是edges数组中的第3条边，记录的是边的编号
		//3 : {1,2} 表示和点3相关的点是edges数组中的第1和第2条边，记录的是边的编号
		//因为边和反向边是成对出现的，假设某条边编号是i，异或1，即 (i^1) 就能得到它的反向边编号 
		private ArrayList<ArrayList<Integer>> nexts;
		
		//高度数组
		private int[] depth;
		
		//记录当前点用到了哪些边，接下来要走的边从哪条开始
		//比如一开始点1有四条边与其相关 {0， 1， 2， 3}
		//从第0条边开始使用，则cur[1] = 0
		//若经过某次操作后，还剩下2和3这两个编号的边可用，则此时cur[1] = 2
		private int[] cur; 

		public Dinic(int nums) {
			N = nums + 1; //在N个点的基础上补一个，则点的编号无论从0还是从1开始都可以
			nexts = new ArrayList<>();
			for (int i = 0; i <= N; i++) { //每个点都有边列表，所以一共N个
				nexts.add(new ArrayList<>());
			}
			edges = new ArrayList<>();
			depth = new int[N];
			cur = new int[N];
		}
		
		//添加边：从u到v的边，可用承载量是r，成对增加的
		//对于无向图来说，如A-B，边的权值为20，则一共要产生四条边：(A,B,20) (B,A,0), (B,A,20),(A,B,0)
		public void addEdge(int u, int v, int r) {
			int m = edges.size(); //先获取edges数组的长度，此时已经存在的边下标就是0~m-1
			edges.add(new Edge(u, v, r)); //将新的边添加到edges数组中
			nexts.get(u).add(m); //u这个点与其相关的边要增加上新添加的边，而新添加的边的在edges数组中的下标就是m 
			edges.add(new Edge(v, u, 0)); //添加反向边
			nexts.get(v).add(m + 1);
		}
		
		//最大网络流算法
		public int maxFlow(int s, int t) {
			int flow = 0;
			while (bfs(s, t)) { //一直循环，直到没有s到t的路径
				Arrays.fill(cur, 0); //表示当前这个点s是从next中与它相关的的哪条边开始的，边权值为0时是不可走的，直接跳过，一开始默认每个点都是从第0号边开始的
				flow += dfs(s, t, Integer.MAX_VALUE); //要传输的流量默认为很大
				Arrays.fill(depth, 0);
			}
			return flow;
		}
		
		//广度优先搜索
		//功能：（1）标记t是否能到；（2）记录高度，标记高度数组
		private boolean bfs(int s, int t) {
			//隐含了每一个s所在的层数都是第0层
			//因为之前初始化depth时，所有的值都是默认为0
		
			//广度优先搜索用队列
			LinkedList<Integer> queue = new LinkedList<>();
			queue.addFirst(s);
			//布尔类型是为了进过队列的点不再进入
			boolean[] visited = new boolean[N];
			//源点，第一个被访问
			visited[s] = true;
			
			while (!queue.isEmpty()) {
				int u = queue.pollLast();
				for (int i = 0; i < nexts.get(u).size(); i++) { //遍历next数组中与当前点u相关的边的编号
					Edge e = edges.get(nexts.get(u).get(i)); //取出边的编号对应的边
					int v = e.to;
					if (!visited[v] && e.available > 0) { //只关心路径权值>0的点
						visited[v] = true;
						depth[v] = depth[u] + 1;
						if (v == t) {
							break;
						}
						queue.addFirst(v);
					}
				}
			}
			return visited[t];
		}

		// 当前来到了s点，s可变
		// 最终目标是t，t固定参数
		// r，收到的任务
		// 收集到的流，作为结果返回，ans <= r
		private int dfs(int s, int t, int r) {
			if (s == t || r == 0) {
				return r;
			}
			int f = 0;
			int flow = 0;
			// s点从哪条边开始试 -> cur[s]
			for (; cur[s] < nexts.get(s).size(); cur[s]++) {
				int ei = nexts.get(s).get(cur[s]);
				//边和反向边都获得
				Edge e = edges.get(ei);
				Edge o = edges.get(ei ^ 1);
				//下一个点高度（层数）比当前点大，才往下走
				//且 下一个点能到t且它完成的任务流量 f 不等于0   Math.min(e.available, r)在任务和边的权值中选择较小的
				if (depth[e.to] == depth[s] + 1 && (f = dfs(e.to, t, Math.min(e.available, r))) != 0) {
					e.available -= f; //边的承载量 - f
					o.available += f; //反向边 + f
					flow += f; //完成的流 + f
					r -= f; //上一个节点派下来的任务 - f 
					if (r <= 0) { //任务完成
						break;
					}
				}
			}
			return flow;
		}
	}

}