16届蓝桥杯算法类知识图谱.pdf
1. 格式打印
%03d:如果是两位数,将会在前面添上一位0
%.2f:会保留两位小数
如果是long,必须在数字后面加上L。
2. 进制转化
2.1. 十进制转任意进制:
十进制转任意进制时,将这个十进制数除以进制数,比如2(也就是十进制转二进制),得到商和一个从0~1的余数,然后再以这个商为被除数,除了进制数2,继续得到商和一个从0~1的余数。以此方式不断相除,直到得到的商为0为止。此时,得到若干个余数,把这些余数按从后到先的顺序排列起来,那么这个排列起来的值即为该十进制转换成二进制的值。计算如图所示:
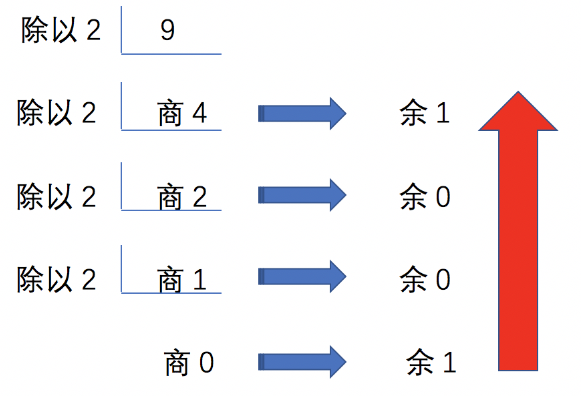
最后得到的余数为二进制的非零的最高位,最先得到的余数为二进制的最低位,可知:十进制数9转换成二进制数为1001。
2.2. 任意进制转十进制:
任意进制转十进制时,以二进制数1001为例:该进制的最低位(右一)的值1就表示实际的十进制值1,次低位(右二)的值0表示进制数2的一次方的0倍即为0,次次低位(右三)的值0表示进制数2的二次方4的0倍即为0,最高位(左一)的值1表示进制数2的三次方8的1倍即为8,以此类推,将每位得到的十进制数相加得到9,该和即为二进制数1001对应的十进制数。计算如图所示:
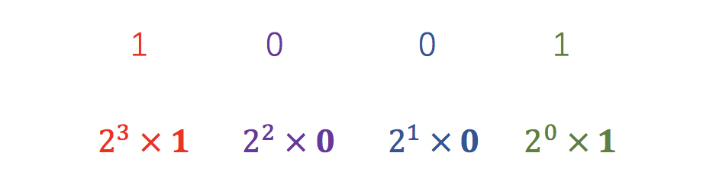
3. 一维前缀和
- 快速求解某区间内的各种形式的和即可使用
- 使用迭代求和
sum[i]=sum[i-1]+num[i]4. 一维差分
- bi = ai-ai-1
其中b1 = a1
- 如果
c是b的前缀和:即,ci = ci-1 + bi - 那么
c就是原数组a
4.1. 常见性质
- 差分数组都是0,说明原数组每个元素都相同
差分数组的前缀和就是原数组- 如果bl + d 与 br+1 - d同时作用,则
c数组就是原数组ai+d的结果 - 对差分的某一个位置减一等价于对原数组此位置及以后的位置减一
4.2. 特殊数列
数列: 1 4 10 20 35
对应的差分数列:1 3 6 10 15
差分数列是等差数列
5. 快读模板
static FastReader in = new FastReader(); // 创建一个静态的 FastReader 对象,用于处理输入
static PrintWriter out = new PrintWriter(System.out); // 创建一个静态的 PrintWriter 对象,用于输出数据
// FastReader 类,用于处理高效的输入
static class FastReader {
static BufferedReader br; // 静态的 BufferedReader,用于高效读取输入
static StringTokenizer st; // 静态的 StringTokenizer,用于将输入字符串分割为标记
// 构造函数,初始化 BufferedReader 以从标准输入读取数据
FastReader() {
br = new BufferedReader(new InputStreamReader(System.in)); // 使用 System.in 作为输入流初始化 BufferedReader
}
// next() 方法,返回下一个字符串标记
String next() {
String str = ""; // 定义一个空字符串,用于存储读取到的行
// 如果 StringTokenizer 为 null 或没有更多标记可读取,读取新行
while (st == null || !st.hasMoreElements()) {
try {
str = br.readLine(); // 使用 BufferedReader 读取一整行输入
} catch (IOException e) { // 捕获可能的 I/O 异常
throw new RuntimeException(e); // 如果发生异常,抛出运行时异常
}
st = new StringTokenizer(str); // 将读取到的行传递给 StringTokenizer 进行分割
}
return st.nextToken(); // 返回 StringTokenizer 的下一个标记
}
// nextInt() 方法,返回下一个整数输入
int nextInt() {
return Integer.parseInt(next()); // 使用 next() 方法读取字符串并转换为整数
}
// nextDouble() 方法,返回下一个双精度浮点数输入
double nextDouble() {
return Double.parseDouble(next()); // 使用 next() 方法读取字符串并转换为双精度浮点数
}
// nextLong() 方法,返回下一个长整数输入
long nextLong() {
return Long.parseLong(next()); // 使用 next() 方法读取字符串并转换为长整数
}
}- StringTokenizer 的分词作用 :
-
StringTokenizer的作用是将一行输入拆分成多个标记,便于依次处理(比如单词或数字)。- 可以理解为:
st是一个“分词器”,根据空格等分隔符来划分输入。
- 总结记忆方法:
-
- 输入原理:
BufferedReader+StringTokenizer= 快速读取并分词。 - 输出原理:
PrintWriter= 快速输出。 - 类型方法:
next()负责读取字符串标记,nextInt()等方法负责类型转换。
- 输入原理:
6. 二维差分
二维差分是在一维差分的基础上推导的公式。
之前学过,差分数组的前缀和就是原数组,由此进行推导即可。
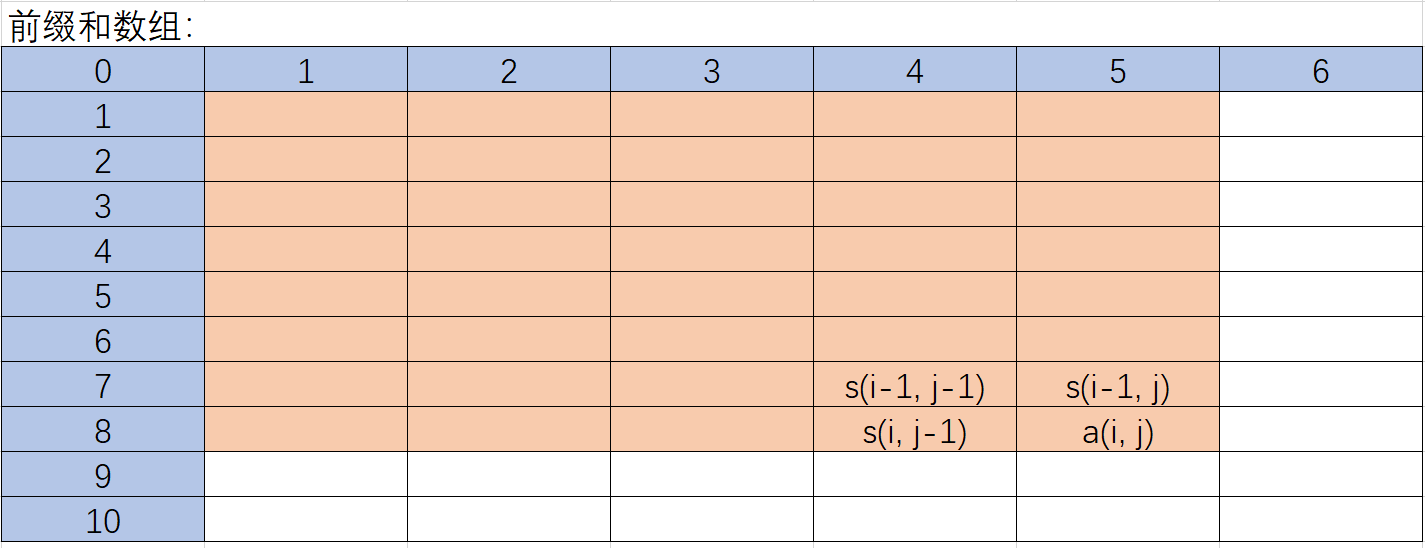
使用 s表示前缀和数组,a表示原数组。
则:
s(i,j) = a(i,j) + s(i-1,j) + s(i,j-1) - s(i-1,j-1)
那么我们现在要求二维差分数组,就:
- 将
原数组看做差分数组 - 将
前缀和看做原数组
具体原因见下图。
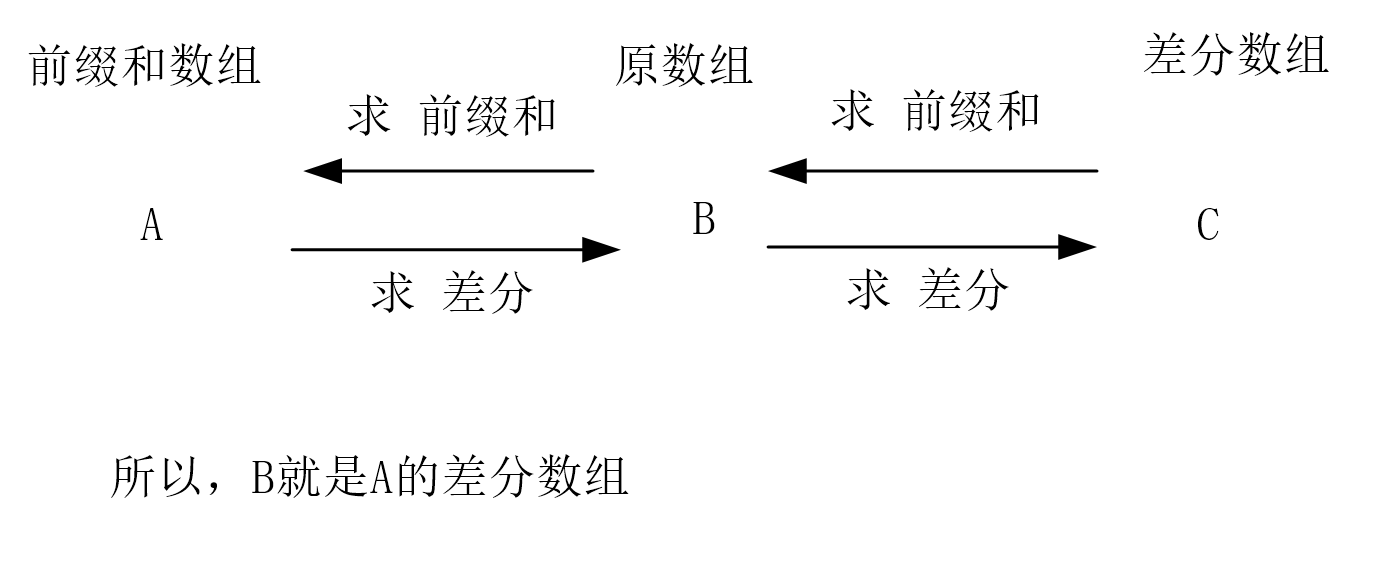
那么,我们要求差分(定为 b),就将差分移到左边(原式中的 a):
a(i,j) = s(i,j) - s(i-1,j) - s(i,j-1) + s(i-1,j-1)
更换为正确的字母后:
b(i,j) = a(i,j) - a(i-1,j) - a(i,j-1) + a(i-1,j-1)
上式就是二维差分的公式。
要求原数组的话,就将 b 求前缀和即可。
6.1. 二维数组对于某个区域加常数 c
使用二维差分数组。
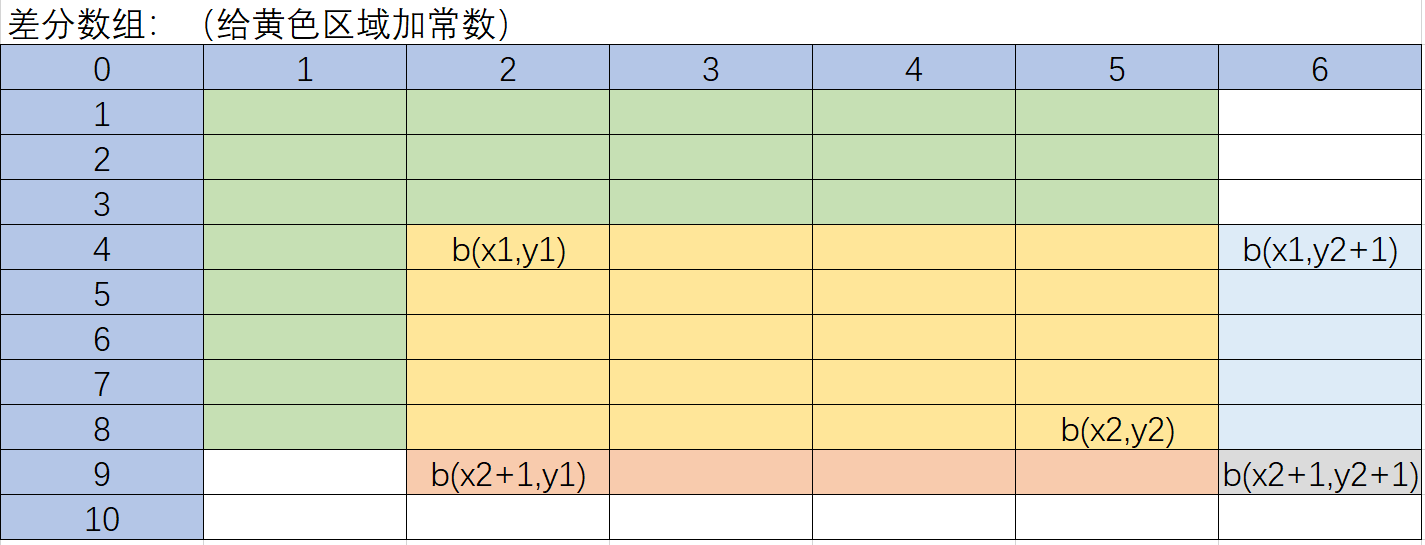
b(x1,y1) += c;
b(x1,y2+1) -= c;
b(x2+1,y1) -= c;
b(x2+1,y2+1) += c;(多减了一次)
之后再对 b 数组求前缀和得到二维原数组。
1. 格式打印
%03d:如果是两位数,将会在前面添上一位0
%.2f:会保留两位小数
如果是long,必须在数字后面加上L。
2. 进制转化
2.1. 十进制转任意进制:
十进制转任意进制时,将这个十进制数除以进制数,比如2(也就是十进制转二进制),得到商和一个从0~1的余数,然后再以这个商为被除数,除了进制数2,继续得到商和一个从0~1的余数。以此方式不断相除,直到得到的商为0为止。此时,得到若干个余数,把这些余数按从后到先的顺序排列起来,那么这个排列起来的值即为该十进制转换成二进制的值。计算如图所示:
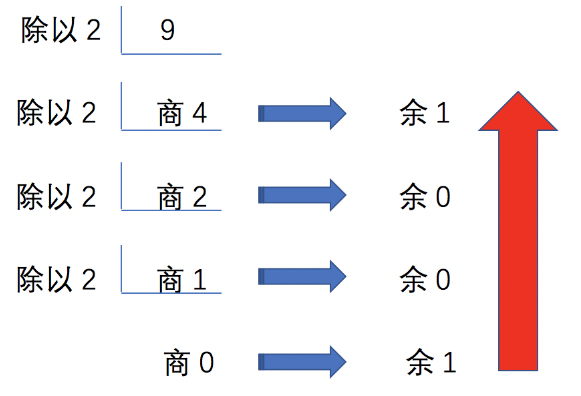
最后得到的余数为二进制的非零的最高位,最先得到的余数为二进制的最低位,可知:十进制数9转换成二进制数为1001。
2.2. 任意进制转十进制:
任意进制转十进制时,以二进制数1001为例:该进制的最低位(右一)的值1就表示实际的十进制值1,次低位(右二)的值0表示进制数2的一次方的0倍即为0,次次低位(右三)的值0表示进制数2的二次方4的0倍即为0,最高位(左一)的值1表示进制数2的三次方8的1倍即为8,以此类推,将每位得到的十进制数相加得到9,该和即为二进制数1001对应的十进制数。计算如图所示:
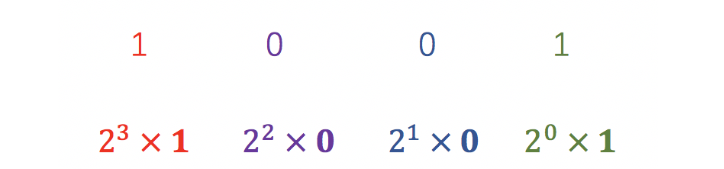
3. 一维前缀和
- 快速求解某区间内的各种形式的和即可使用
- 使用迭代求和
sum[i]=sum[i-1]+num[i]4. 一维差分
- bi = ai-ai-1
其中b1 = a1
- 如果
c是b的前缀和:即,ci = ci-1 + bi - 那么
c就是原数组a
4.1. 常见性质
- 差分数组都是0,说明原数组每个元素都相同
差分数组的前缀和就是原数组- 如果bl + d 与 br+1 - d同时作用,则
c数组就是原数组ai+d的结果 - 对差分的某一个位置减一等价于对原数组此位置及以后的位置减一
4.2. 特殊数列
数列: 1 4 10 20 35
对应的差分数列:1 3 6 10 15
差分数列是等差数列
5. 快读模板
static FastReader in = new FastReader(); // 创建一个静态的 FastReader 对象,用于处理输入
static PrintWriter out = new PrintWriter(System.out); // 创建一个静态的 PrintWriter 对象,用于输出数据
// FastReader 类,用于处理高效的输入
static class FastReader {
static BufferedReader br; // 静态的 BufferedReader,用于高效读取输入
static StringTokenizer st; // 静态的 StringTokenizer,用于将输入字符串分割为标记
// 构造函数,初始化 BufferedReader 以从标准输入读取数据
FastReader() {
br = new BufferedReader(new InputStreamReader(System.in)); // 使用 System.in 作为输入流初始化 BufferedReader
}
// next() 方法,返回下一个字符串标记
String next() {
String str = ""; // 定义一个空字符串,用于存储读取到的行
// 如果 StringTokenizer 为 null 或没有更多标记可读取,读取新行
while (st == null || !st.hasMoreElements()) {
try {
str = br.readLine(); // 使用 BufferedReader 读取一整行输入
} catch (IOException e) { // 捕获可能的 I/O 异常
throw new RuntimeException(e); // 如果发生异常,抛出运行时异常
}
st = new StringTokenizer(str); // 将读取到的行传递给 StringTokenizer 进行分割
}
return st.nextToken(); // 返回 StringTokenizer 的下一个标记
}
// nextInt() 方法,返回下一个整数输入
int nextInt() {
return Integer.parseInt(next()); // 使用 next() 方法读取字符串并转换为整数
}
// nextDouble() 方法,返回下一个双精度浮点数输入
double nextDouble() {
return Double.parseDouble(next()); // 使用 next() 方法读取字符串并转换为双精度浮点数
}
// nextLong() 方法,返回下一个长整数输入
long nextLong() {
return Long.parseLong(next()); // 使用 next() 方法读取字符串并转换为长整数
}
}- StringTokenizer 的分词作用 :
-
StringTokenizer的作用是将一行输入拆分成多个标记,便于依次处理(比如单词或数字)。- 可以理解为:
st是一个“分词器”,根据空格等分隔符来划分输入。
- 总结记忆方法:
-
- 输入原理:
BufferedReader+StringTokenizer= 快速读取并分词。 - 输出原理:
PrintWriter= 快速输出。 - 类型方法:
next()负责读取字符串标记,nextInt()等方法负责类型转换。
- 输入原理:
6. 二维差分
二维差分是在一维差分的基础上推导的公式。
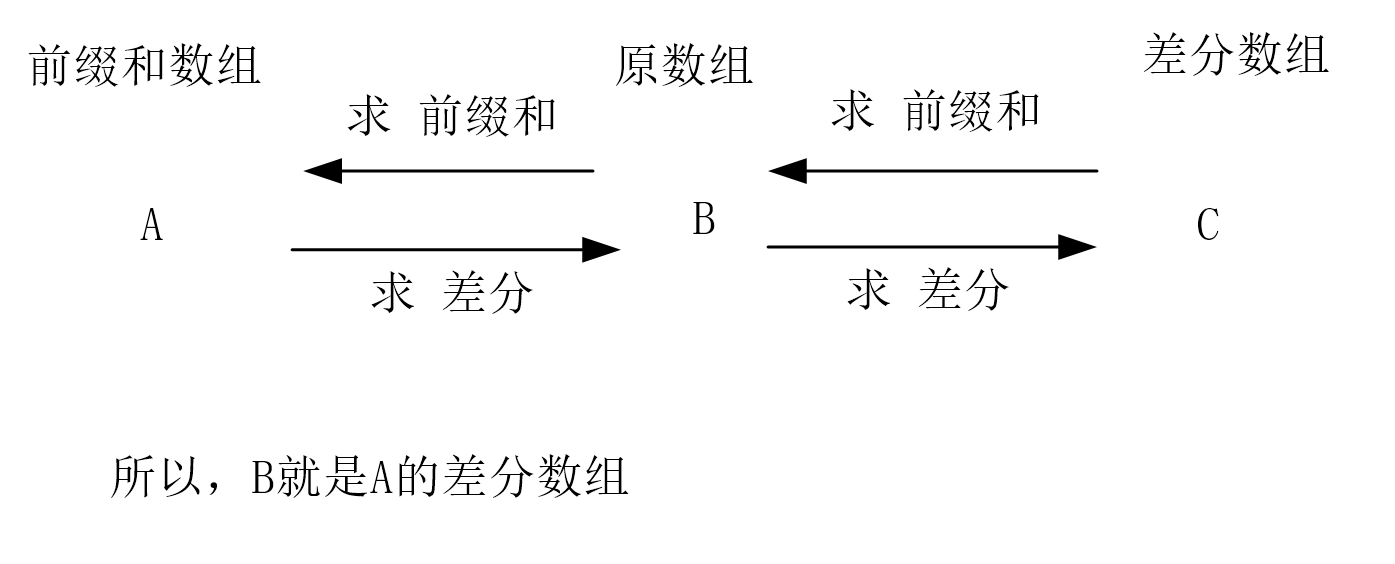
之前学过,差分数组的前缀和就是原数组,由此进行推导即可。

使用 s表示前缀和数组,a表示原数组。
则:
s(i,j) = a(i,j) + s(i-1,j) + s(i,j-1) - s(i-1,j-1)
那么我们现在要求二维差分数组,就:
- 将
原数组看做差分数组 - 将
前缀和看做原数组
具体原因见下图。
那么,我们要求差分(定为 b),就将差分移到左边(原式中的 a):
a(i,j) = s(i,j) - s(i-1,j) - s(i,j-1) + s(i-1,j-1)
更换为正确的字母后:
b(i,j) = a(i,j) - a(i-1,j) - a(i,j-1) + a(i-1,j-1)
上式就是二维差分的公式。
要求原数组的话,就将 b 求前缀和即可。
6.1. 二维数组对于某个区域加常数 c
使用二维差分数组。
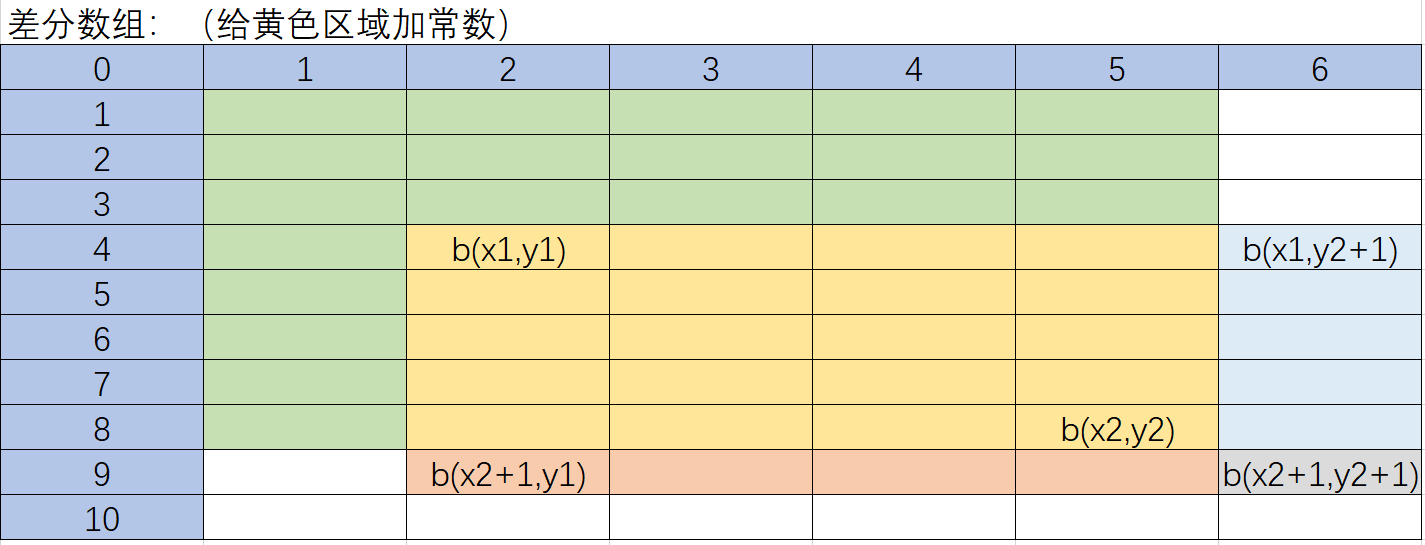
b(x1,y1) += c;
b(x1,y2+1) -= c;
b(x2+1,y1) -= c;
b(x2+1,y2+1) += c;(多减了一次)
之后再对 b 数组求前缀和得到二维原数组。