计算图 Computational Graph
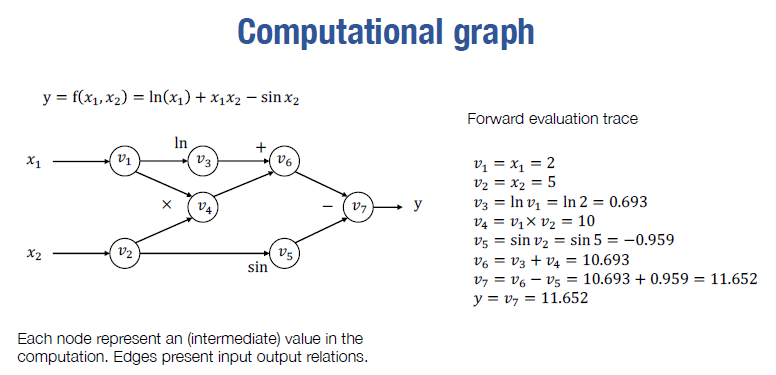
- 图上的每个节点代表一个中间值
- 边事输入输出的关系
forward 求导 forward mode AD
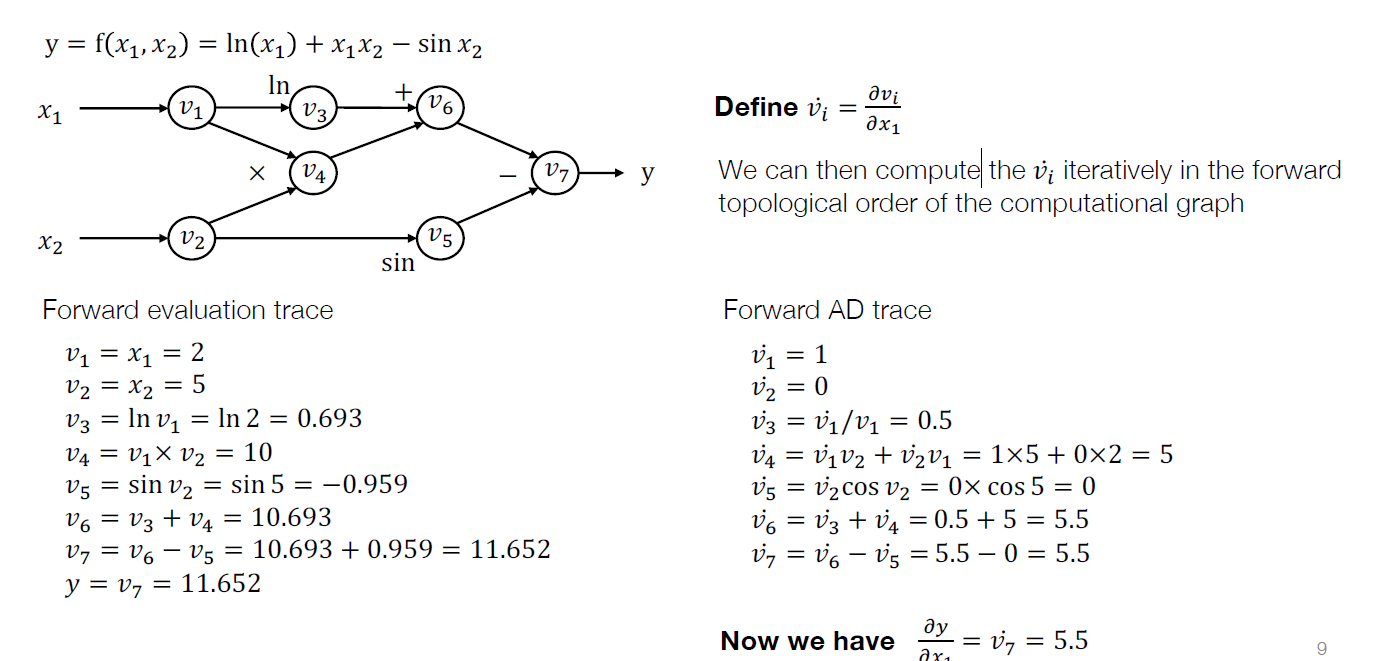
上图中从前向后,一步一步计算每个中间值对 x1的偏导,那么计算到 v7,就得到了整个函数对于 x1的偏导。
有limitation
- 对一个参数 xi 运行一次可以得到这个参数,可以得到多个输出对参数xi的求导结果。
- 当参数比较少,输出比较多时,使用这个方法比较好
- 但是,大多数情况下,我们仅仅有一个输出 loss,但是会有很多参数
- 有n个参数,需要运行n次forward求导
Reverse Mode AD 求导
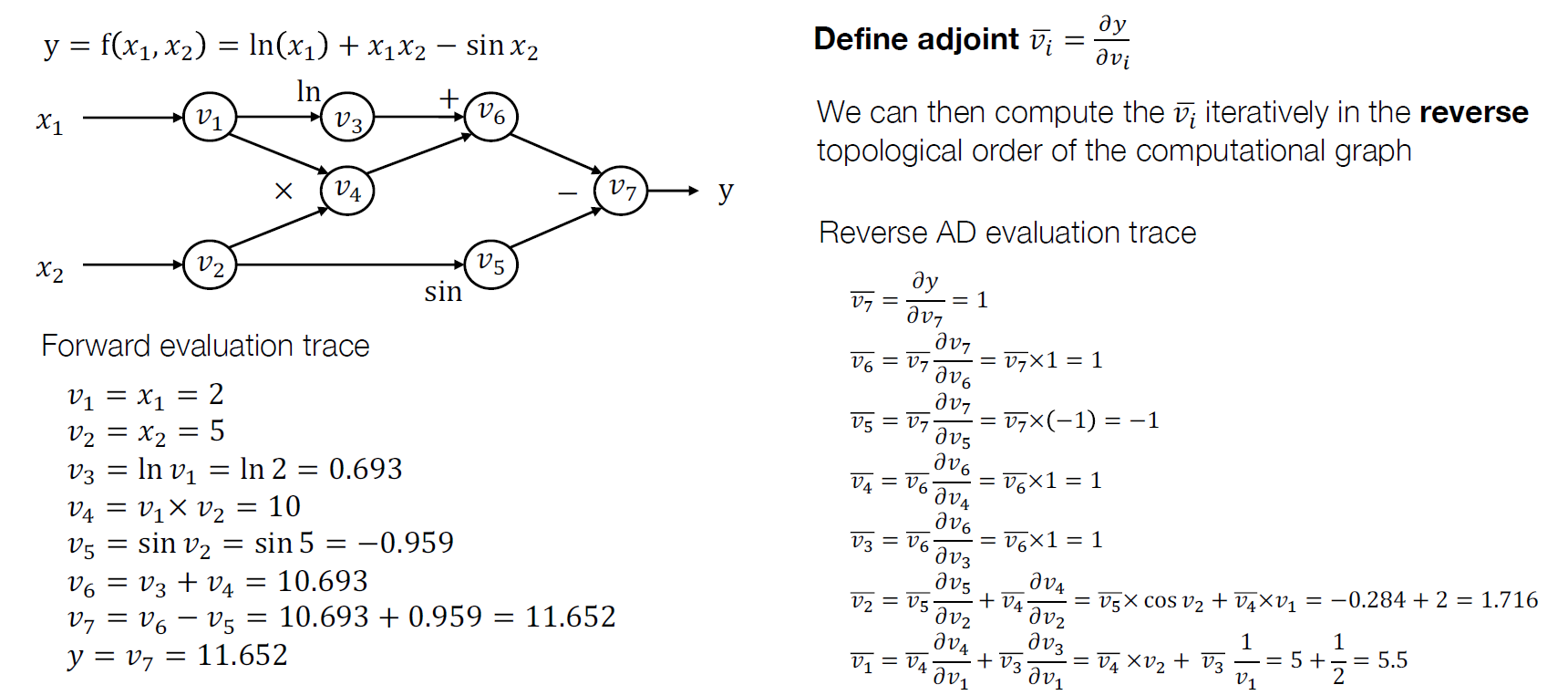
反向求导,实际上事对链式法则的运用
v 1 ˉ = ∂ y ∂ v 1 = ∂ y ∂ v i ∂ v i ∂ v 1 = ∂ y ∂ v i ∂ v i ∂ v i − 1 ∂ v i − 2 ∂ v 1 = ∂ y ∂ v i ∂ v i ∂ v i − 1 ∂ v i − 2 ∂ v i − 3 . . . ∂ v 2 ∂ v 1 \bar{v_1} = \frac{\partial y}{\partial v1} = \frac{\partial y}{\partial v_i}\frac{\partial v_i}{\partial v1} = \frac{\partial y}{\partial v_i}\frac{\partial v_i}{\partial v_{i-1}}\frac{\partial v_{i-2}}{\partial v1} = \frac{\partial y}{\partial v_i}\frac{\partial v_i}{\partial v_{i-1}}\frac{\partial v_{i-2}}{\partial v_{i-3}}...\frac{\partial v_{2}}{\partial v1} v1ˉ=∂v1∂y=∂vi∂y∂v1∂vi=∂vi∂y∂vi−1∂vi∂v1∂vi−2=∂vi∂y∂vi−1∂vi∂vi−3∂vi−2...∂v1∂v2
其中很多的中间结果可以被重用,就减少了我们的很多开销。
- 每个节点接收到上游传来的偏导,如节点 v i v_i vi 的偏导 v i ˉ = ∂ y ∂ v i \bar{v_i} = \frac{\partial y}{\partial v_i} viˉ=∂vi∂y 来自于上游偏导的输出
- 每个节点根据下游节点,求一个 partial adjoint v i → j ‾ = v j ˉ ∂ v j ∂ v i \overline{v_{i\to j}} = \bar{v_j}\frac{\partial v_j}{\partial v_i} vi→j=vjˉ∂vi∂vj 再传给下游节点
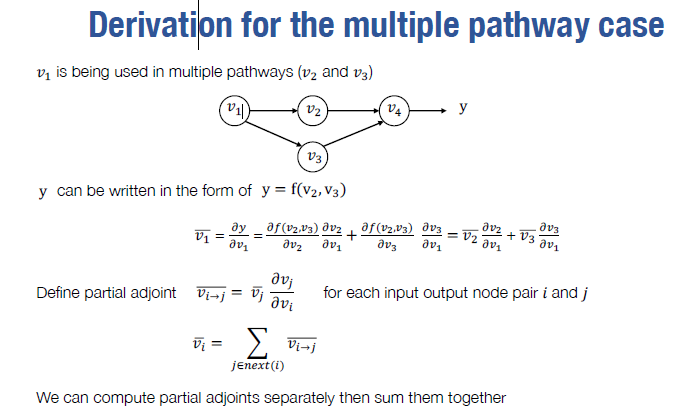
对于有多个上游节点的情况,会得到多个上游节点的梯度,如何处理?
v
i
ˉ
=
∑
i
∈
n
e
x
t
(
i
)
v
i
→
j
‾
\bar{v_i} = \sum_{i\in next(i)}\overline{v_{i\to j}}
viˉ=i∈next(i)∑vi→j
下游节点将上游传来的所有偏导相加 (partial adjoint 我没有很好的翻译方式)
下面有证明;