1写在前面的话

这篇文章属于地面分割领域非常经典的一篇论文，论文具有速度快，在一定程度能适应有坡度的地形，文章主要分为两个阶段：数据投影分块，在分块中寻找地面点。

2点云投影分块

我们首先将点云投影到xy平面，并将其划分为一定数量的点云块，以此来实现地面分割，如图1所示。我们引入了参数$\Delta a$，该参数描述了每个分割块的角度。因此，我们得出了$M=2\pi /\Delta a$个分割块。分割块对应的原始点云索引用segment（pi）表示，很容易计算:
$$\mathrm{segment}\left(p_i\right)=\frac{\mathrm{atan}2\left(y_i,x_i\right)}{\Delta \alpha }$$
$\mathrm{atan}2\left(y_i,x_i\right)$表示点云与原点构成的线段与x正方向的夹角，其值在$[0,2\pi ]$之间。其过程如下图：

我们将segment（pi）对应的3d点云集合表示为：
P s = { p i ∈ P ∣ segment ⁡ ( p i ) = s } P_s=\left\{p_i \in P \mid \operatorname{segment}\left(p_i\right)=s\right\} Ps​={pi​∈P∣segment(pi​)=s}
这里的$P_s$是通过分块的索引对应的原始点云为3d点云，而不是2d点云。
为了获得适合于地面平面估计，我们将同一分割块Ps中的所有点云继续划分为许多$bi{n}_j^s,j=\mathrm{1...}$。我们用$r^{m}i{n}_j$和$r^{m}a{x}_j$来表示某一bin覆盖的最小和最大距离。然后如果某一点云满足$r_j^{\min }\le \sqrt{x_i^2+y_i^2}<r_j^{\max }$，将其加入到该bin中，直至划分为整个分割块。如下图：

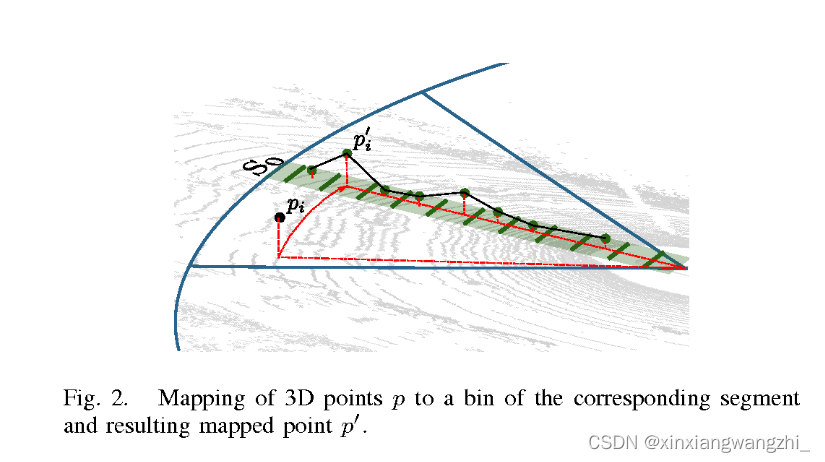
对于一个bin中的点云，我们重新定义一个二维集合：
$$P_{b_j^s}^{\prime }=\left\{p_i^{\prime }={\left(\sqrt{x_i^2+y_i^2}{z}_i\right)}^T\mid p_i\in P_{b_j^s}\right\}$$
一般而言每个bin($P_{b_j^s}^{\prime }$)中包含很多点，只取一个点表示bin，这个点称为prototype point， 记为$p_{b_j^s}^{\prime }$，本文取得z值最小的点。选择prototype point能够简化3d点云提取地面点提取过程，更重要的是，点云地面提取过程和点云数量无关，只和Δa以及bin的数量有关。

3地面点云分割

通过对每个分割块中的prototype points拟合直线提取地面点。这里采用文献[11]所描述的增量式算法。对于直线$y=mx+b$，当其满足以下几个条件时，考虑其是地面平面的一部分：

• 1 直线的斜率m不超过阈值$T_m$，即地面不可能是完全水平的。
• 2 对于小斜率的直线，即$ m<T_{m_{small}} $时，截距$b$不能超过阈值$T_b$。因为如果$b$太大，拟合出来的平面就不在地面上了。
• 3 拟合的直线误差不能超过阈值$T_{r}mse$
• 4 当前直线的起始点，距离上一条拟合出来的直线的距离，不能超过阈值，确保两条直线之间是平滑连接的。
  下图为拟合直线的具体方法：
  在这里插入图片描述

通过上述方法对于每个分割块，我们能得到很多直线方程，其集合记为$L_s=(m_i,b_i)$.$L_s$表示分割块的ground plane。现在我们可以通过$L_s$判断点云是否属于地面点。在分割块的每个点云中计算点云到所有直线端点的距离：
(1)如果该点云到最近的直线端点距离都很大，说明点云距离直线很远，此时采用保守的方法判断该点是否是地面点。
(1)否则,如果点到直线的距离小于阈值，则判断为地面点。

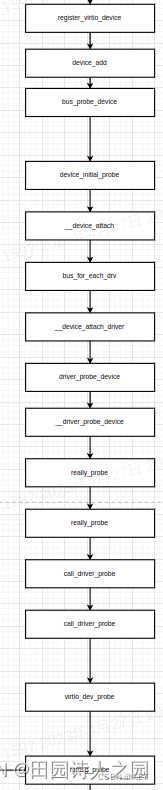
4核心代码阅读

投影分块

//start_index，end_index当前segment中点云起始和终止索引
//cloud所有3d点云
void GroundSegmentation::insertionThread(const PointCloud& cloud,
                                         const size_t start_index,
                                         const size_t end_index) 
{
  const double segment_step = 2*M_PI / params_.n_segments;//计算Δa
  //根据参数指定的每个分割块最大距离和最小距离、bin的数目，计算bin的步长
  const double bin_step = (sqrt(params_.r_max_square) - sqrt(params_.r_min_square))
      / params_.n_bins;
  const double r_min = sqrt(params_.r_min_square);

  for (unsigned int i = start_index; i < end_index; ++i) 
  {
      //计算平面距离range
    pcl::PointXYZ point(cloud[i]);
    const double range_square = point.x * point.x + point.y * point.y;
    const double range = sqrt(range_square);
    //如果range在指定的分割块（segment）的范围内再进行别的计算
    if (range_square < params_.r_max_square && range_square > params_.r_min_square) 
    {
        //计算平面夹角
      const double angle = std::atan2(point.y, point.x);
      //计算当前点云所有哪个bin
      const unsigned int bin_index = (range - r_min) / bin_step;
      //计算当前点云所有哪个分割块
      const unsigned int segment_index = (angle + M_PI) / segment_step;
      //防止越界
      const unsigned int segment_index_clamped = segment_index == params_.n_segments ? 0 : segment_index;
     //把这个点云放到对应的分割块的对应的bin中，这里addPoint存的是最低点
      segments_[segment_index_clamped][bin_index].addPoint(range, point.z);
      //记录该点云所在的分割块及bin
      bin_index_[i] = std::make_pair(segment_index_clamped, bin_index);
    }
    //如果range不在指定的分割块（segment）的范围内不计算
    else 
    {
      bin_index_[i] = std::make_pair<int, int>(-1, -1);
    }
    //构建二维的集合，存放平面距离和z值
    segment_coordinates_[i] = Bin::MinZPoint(range, point.z);
  }
}

直线拟合代码

//增量式拟合直线，输出为lines_：保存直线的两个端点(d,z)
void Segment::fitSegmentLines() 
{
  // Find first point.bins_：当前分割块segment对应的所有二维集合（d,z）,每个bin只有一个点
  auto line_start = bins_.begin();
  while (!line_start->hasPoint()) {
    ++line_start;
    // Stop if we reached last point.
    if (line_start == bins_.end()) return;
  }
  // Fill lines.
  bool is_long_line = false;
  double cur_ground_height = -sensor_height_;//地面高度
  //当前直线集合中的所有二维点
  std::list<Bin::MinZPoint> current_line_points(1, line_start->getMinZPoint());
  LocalLine cur_line = std::make_pair(0,0);
  //从第二个bin开始遍历分割块的所有bin
  for (auto line_iter = line_start+1; line_iter != bins_.end(); ++line_iter)
  {
    if (line_iter->hasPoint()) 
    {
        //找到该bin的二维点，d，z
      Bin::MinZPoint cur_point = line_iter->getMinZPoint();
      //计算当前bin与上个bin的d之差，如果大于阈值，则认为是一个长直线
      if (cur_point.d - current_line_points.back().d > long_threshold_)
      {
          is_long_line = true;
      }
      //如果当前直线多于两个点
      if (current_line_points.size() >= 2)
      {
        // Get expected z value to possibly reject far away points.
        double expected_z = std::numeric_limits<double>::max();
        if (is_long_line && current_line_points.size() > 2) 
        {
          expected_z = cur_line.first * cur_point.d + cur_line.second;
        }
        //存放bin（二维点）
        current_line_points.push_back(cur_point);
        //利用所有点去拟合直线，返回斜率m和截距b
        cur_line = fitLocalLine(current_line_points);
        //计算点到直线的最大距离（误差）
        const double error = getMaxError(current_line_points, cur_line);
        // Check if not a good line.
        //如果不是一个符合条件的直线
        if (error > max_error_ ||
            std::fabs(cur_line.first) > max_slope_ ||
            (current_line_points.size() > 2 && std::fabs(cur_line.first) < min_slope_) ||
            is_long_line && std::fabs(expected_z - cur_point.z) > max_long_height_) 
        {
          // Add line until previous point as ground.
            //删除刚刚放进来的点
          current_line_points.pop_back();
          //这里是干嘛的??
          // Don't let lines with 2 base points through.
          if (current_line_points.size() >= 3)
          {
              //删除当前bin之后重新拟合直线
            const LocalLine new_line = fitLocalLine(current_line_points);
            //重新拟合的直线也不一定是好的，为什么还pushback？
            lines_.push_back(localLineToLine(new_line, current_line_points));
            cur_ground_height = new_line.first * current_line_points.back().d + new_line.second;
          }
          // Start new line.
          is_long_line = false;
          //清空当前直线所有bin
          current_line_points.erase(current_line_points.begin(), --current_line_points.end());
         //回到上个bin
          --line_iter;
        }
        // Good line, continue.
        else { }
      }
      //如果点云数量少于2，添加点
      else 
      {
        // Not enough points.
          //添加的点要求距离不能太远，并且不能距离地面太远
        if (cur_point.d - current_line_points.back().d < long_threshold_ &&
            std::fabs(current_line_points.back().z - cur_ground_height) < std::abs(max_start_height_)) 
        {
          // Add point if valid.
          current_line_points.push_back(cur_point);
        }
        else 
        {
          // Start new line.
          current_line_points.clear();
          current_line_points.push_back(cur_point);
        }
      }
    }
  }
  // Add last line.
  //如果bin没有点云则中断该次直线拟合
  if (current_line_points.size() > 2) {
    const LocalLine new_line = fitLocalLine(current_line_points);
    lines_.push_back(localLineToLine(new_line, current_line_points));
  }
}

//计算直线的端点，这里的端点是通过直线方程计算得到的理论值，不是点云的实际值
Segment::Line Segment::localLineToLine(const LocalLine& local_line,const std::list<Bin::MinZPoint>& line_points) 
{
  Line line;
  const double first_d = line_points.front().d;
  const double second_d = line_points.back().d;
  const double first_z = local_line.first * first_d + local_line.second;
  const double second_z = local_line.first * second_d + local_line.second;
  line.first.z = first_z;
  line.first.d = first_d;
  line.second.z = second_z;
  line.second.d = second_d;
  return line;
}

分割地面点云

void GroundSegmentation::assignClusterThread(const unsigned int &start_index,
                                             const unsigned int &end_index,
                                             std::vector<int> *segmentation) 
{
  const double segment_step = 2*M_PI/params_.n_segments;
  for (unsigned int i = start_index; i < end_index; ++i) 
  {
      //segment_coordinates_存放的是所有点的二维坐标（在投影分块过程中已经进行处理了）
    //找到点云对应的二维坐标(d,z)
      Bin::MinZPoint point_2d = segment_coordinates_[i];
      //找到点云所在的分块segment的索引
    const int segment_index = bin_index_[i].first;
    if (segment_index >= 0) 
    {
        //计算点云到所在的分块segment的直线的距离
      double dist = segments_[segment_index].verticalDistanceToLine(point_2d.d, point_2d.z);
      // Search neighboring segments.
      int steps = 1;
      while (dist < 0 && steps * segment_step < params_.line_search_angle) {
        // Fix indices that are out of bounds.
        int index_1 = segment_index + steps;
        while (index_1 >= params_.n_segments) index_1 -= params_.n_segments;
        int index_2 = segment_index - steps;
        while (index_2 < 0) index_2 += params_.n_segments;
        // Get distance to neighboring lines.
         //计算点云到所在的分块segment的相邻两个segment的直线的距离（这里和论文稍有不同）
        const double dist_1 = segments_[index_1].verticalDistanceToLine(point_2d.d, point_2d.z);
        const double dist_2 = segments_[index_2].verticalDistanceToLine(point_2d.d, point_2d.z);
        //经过上述计算一共有3个dist，取最小的dist
        if (dist_1 >= 0) {
          dist = dist_1;
        }
        if (dist_2 >= 0) {
          // Select smaller distance if both segments return a valid distance.
          if (dist < 0 || dist_2 < dist) {
            dist = dist_2;
          }
        }
        ++steps;
      }
      //距离小于阈值则判定为地面点
      if (dist < params_.max_dist_to_line && dist != -1) {
        segmentation->at(i) = 1;
      }
    }
  }
}


//计算到最近的直线的距离，这里利用直线拟合（void Segment::fitSegmentLines()）的结果line_变量
double Segment::verticalDistanceToLine(const double &d, const double &z) {
  static const double kMargin = 0.1;
  double distance = -1;
  //这里写的有点疑问
  for (auto it = lines_.begin(); it != lines_.end(); ++it) 
  {
    if (it->first.d - kMargin < d && it->second.d + kMargin > d) 
    {
      const double delta_z = it->second.z - it->first.z;
      const double delta_d = it->second.d - it->first.d;
      const double expected_z = (d - it->first.d)/delta_d *delta_z + it->first.z;
      distance = std::fabs(z - expected_z);
    }
  }
  return distance;
}

5实验效果

原始点云：(存在一定坡度)

地面分割：（对坡度适用性不是很好）

参考

原文：《Fast Segmentation of 3D Point Clouds for Ground Vehicles》
github
博客1
2
3
4