1.斐波那契数列

分析：

斐波那契数列又称兔子数列，其原理来源于兔子繁殖，成年后的兔子可以不断繁殖新的兔子，
数列项数：1 1 2 3 5 8 13 21 34 55 89…
通过数列，相信你也发现了规律，从第三项开始，每一项=前两项之和。这个递推式就很好找了。
递推式:a[n] = a[n - 1] + a[n - 2];

代码：

#include<bits/stdc++.h>
using namespace std;
int rabbit(int i) {
	if(i==1) return 0;
	else if(i==2||1==3) return 1;
	else return rabbit(i-1)+rabbit(i-2);
}
int main(int i){
	cin>>i;
	cout<<rabbit(i);
}

2.平面分割问题

分析：

此题经常在数学考试中遇到，我们利用贪心思想，每增加一个椭圆，最好的情况就是能分割到已经有的每一个椭圆。
递推式：a[n] = a[n - 1] + 2(n - 1);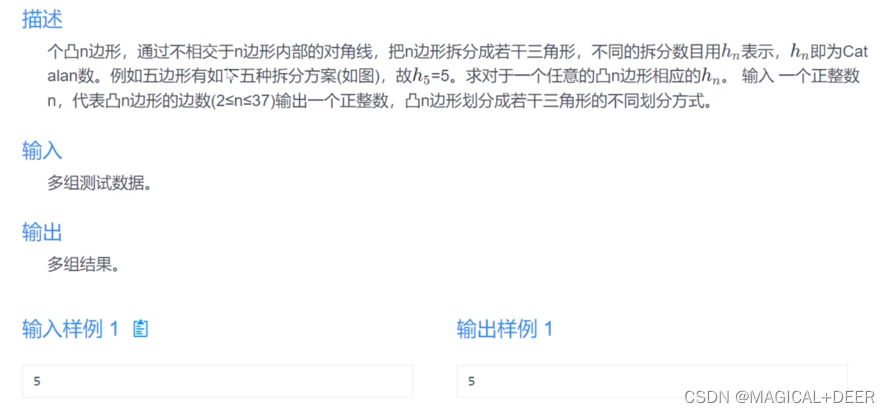

3.汉诺塔问题

分析：

此题较为简单，只需要输出汉诺塔的次数就可以了。我们可以通过递推得到关系式。
我们可以把初始时的圆盘分为两部分:最底下的一个和上面的圆盘。这样的话，上面的圆盘也可以这样分，直到只剩下一个圆盘，根据一个圆盘需要移动的次数为1，我们可以通过递归回溯的方式不断得到后续的答案。

递推式：a[n] = 2a[n - 1] + 1;

4.卡特兰数

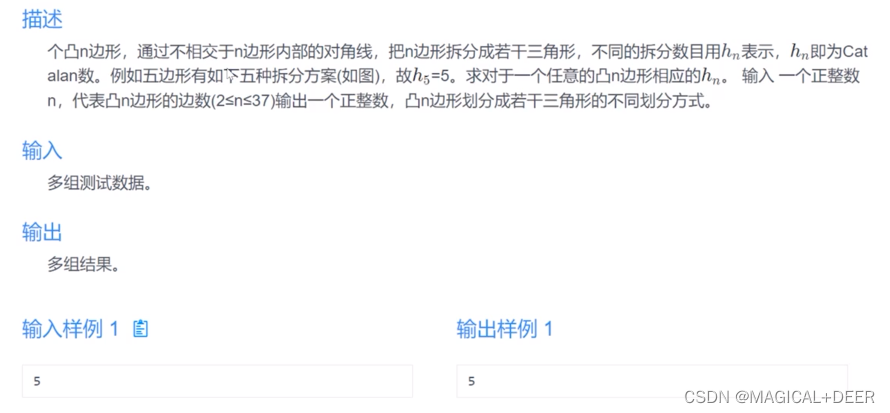
分析：

这是一道典型的卡特兰数的题目：

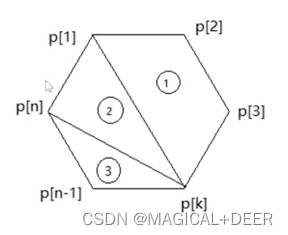
我们可以先确定三角形的两个顶点，由剩余的一个顶点可以算出方案的总数。当然，思路和以上情况相似，如图，先确定3号三角形，它的情况是p[2]-p[n-1]的顶点个数。确定下来后，我们重复上面的步骤，先确定两个点，第三点的方案数 = p[k]-p[n-1] 的个数，=上一种情况-1.利用加法原理整合得到递推式
递推式：

5.第二类斯特林数

待更新

总结：

其实递推和递归原理上近似，使用时经常搭配在一起。如：递推需要递归函数实现，而递归则需要递推式，两者相通。
这几个“模型”，很多思想都是将一个整体分为最后一个和上面的全部，然后不断分下去，得到结果。