概述

• 红黑树是一种自平衡的二叉查找树，是计算机科学中用到的一种数据结构。
• 1972年出现的，当时被称之为平衡二叉B树。在1978年被修改为红黑树。
• 红黑树是一种特殊的二叉查找树，红黑树上的每一个节点都有存储位表示节点的颜色。
• 每一个节点可以是红或者黑。
• 红黑树不是高度平衡的，它的平衡是通过“红黑规则”进行实现的。

 平衡二叉树VS红黑树

• 平衡二叉树
  • 高度平衡
  • 当左右子树高度差超过1，通过旋转保持平衡
• 红黑树
  • 是一个二叉查找树
  • 不是高度平衡的
  • 通过特有的“红黑规则”保持平衡

红黑树的红黑规则

•  一个节点要么红色、要么是黑色的
• 根节点必须是黑色的
• 如果一个节点没有子节点或者父节点，则该节点相应的指针属性值为 Nil ，这些 Nil 被视作叶节点，每一个叶节点(Nil)是黑色的
• 如果某个节点是红色的，那么它的子节点必须是黑色的（不能出现两个红色节点相连的情况）
• 对每个节点，从该节点到其所有的后代叶节点的简单路径上【就是从该节点到叶节点的每一条路径上】，均包含相同数目的黑色节点

如图：

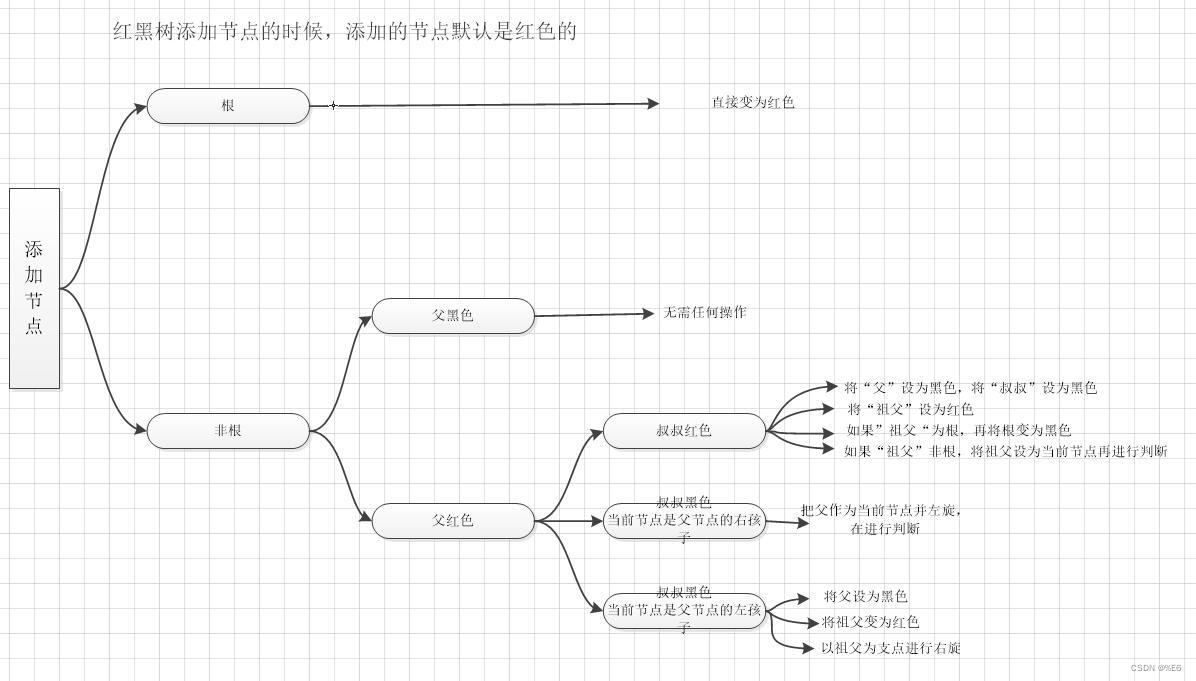
 红黑树添加节点的规则

• 默认颜色：添加节点默认是红色的（效率高）