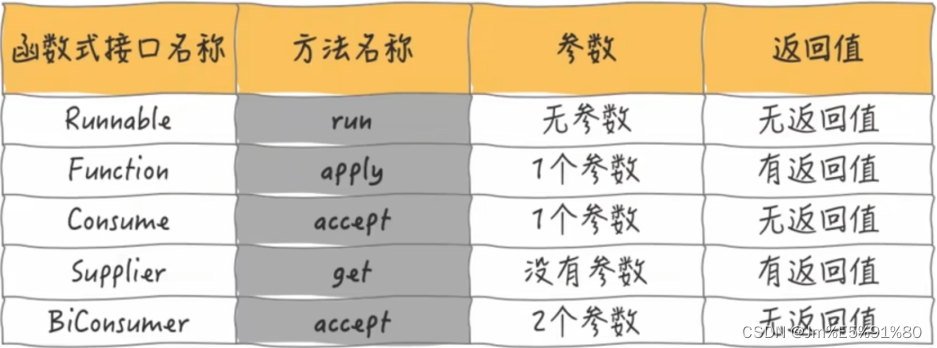
1.减操作(ACWING)

若有 a b c d e f g 几个数,
先对位置d操作 变成 a b c d - e f g
再对c操作 变成 a b c - (d-e) f g
仔细分析后得出结论:对于第一个数如a, 它一定为正数,第二个数b,一定为负数,而其他数一定可以通过一些操作被加或者被减, 将题意转化为了改变某个数(>2)的正负性得到 t
dp[ i ][ j ]表示前i个数的和为 j 的第 i 个数之前的符号
核心DP代码
f[1][a[1] + base] = 1;//防止负下标
f[2][a[1] - a[2] + base] = -1;
for(int i = 3; i <= n; i ++)
{
for(int j = -10000 + base; j <= 10000 + base; j ++)
{
if(f[i - 1][j] != 0)
{
f[i][j + a[i]] = 1;
f[i][j - a[i]] = -1;
}
}
}另进行操作的位置一定是符号为正的位置
2.旅行(ACWING)

最长公共子序列 + 输出所有方案
用DFS来输出所有方案,加一个剪枝
f [ i ][ j ] 表示 a 串的前 i 个字母 和 b 串的前 j 个字母的最大相同长度
fa[ i ][ j ] 表示 a 串的前 i 个字符中字母 j + 'a' 出现的最后位置
fb[ i ][ j ] 表示 b 串的前 i 个字符中字母 j + 'a' 出现的最后位置
在找方案的时候,递归下标和长度去找,如在找 a 串前 la 个字符中和 b 串前 lb 个字符有 k 个相同的方案的时候,枚举第 k 个相同的为哪个字母,设为字母 c,那么对于a来说, 选择la之前的靠近la的 c 显然最好,b同理,这刚好是处理的 fa 和 fb 数组
核心DFS代码,因为最长公共子序列就是那个模板
void dfs(int x, int y, int k)
{
if (k == 0)
{
ed.pb(string(ans + 1));
return;
}
for (int i = 0; i < 26; ++i)
{
int a = fa[x][i], b = fb[y][i];
if (f[a][b] != k)
continue;
ans[k] = 'a' + i;
dfs(a - 1, b - 1, k - 1);
}
}自己想想不到用DFS,因为感觉复杂度太大,但没想到还挺快
可能那个剪枝优化了很多状态吧
3.花匠(牛客)

f[ i ][ 0 / 1] 表示到以第 i 个位置结尾是上升 / 下降的最大长度
考虑状态如何转移
对于下降的来说,如果当前点小于上一个点, 即 i - 1 到 i 是下降的,那么需要 i - 2 到 i - 1 是上升的, 否则下降的不能选这个点结尾
if(a[i] < a[i - 1])
f[i][1] = f[i - 1][0] + 1;
else
f[i][1] = f[i - 1][1];对于上升 的来说,如果当前点大于上一个点, 即 i - 1 到 i 是上升的,那么需要 i - 2 到 i - 1 是下降的, 否则上升的不能选这个点结尾
if(a[i] > a[i - 1])
f[i][0] = f[i - 1][1] + 1;
else
f[i][0] = f[i - 1][0];4.愤怒(牛客)

f [ i ][ j ] 表示第一个序列的左括号比右括号多 j 个的合法方案
当读到一个符号,可以选择把它放在第一个还是第二个中
如果是左括号,状态dp[ i ] [ 0 ]只能给第二个序列
而dp [ i ][ j ]可以给第二个序列或者自己留下
if(s[i] == '(')
{
top ++;
dp[i][0] = dp[i - 1][0];//把(直接给了第二个序列
for(int j = 1; j <= top; j ++)
dp[i][j] = (dp[i - 1][j] + dp[i - 1][j - 1]) % 2333;//给了+自己要
}else
{
top --;
for(int j = top; j >= 0; j --)
dp[i][j] = (dp[i - 1][j] + dp[i - 1][j + 1]) % 2333;//给了+自己要
}5.psd面试(牛客)
最长回文子序列
dp[ i ][ j ] 表示 i --- j 这段内的最长回文子串
int n = s.length();
for(int i = n - 1; i >= 0; i --)//枚举起点
{
for(int j = 1; j + i < n; j ++)//枚举区间长度
{
if(s[i] == s[j + i])
dp[i][j + i] = dp[i + 1][j + i - 1] + 2;
else
dp[i][j + i] = max(dp[i + 1][j + i], dp[i][j + i - 1]);
}
}6.找硬币
这道题为什么这么抽象啊
用dp[ i ]表示用最大面额为 i 的凑出答案的最小硬币数
初始化:dp[ 1 ] 表示用 1 来凑出每个物品, 那么初始答案就是所有的物品花费累加和
如果用 2 的纸币需要 10 个,那么用面额为 4 的 需要五个,所以可以用大面额的去更新减少小面额需要的
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int n, maxn, ans = 10000000, a[55], dp[100010];
int main()
{
memset(dp, 0x3f, sizeof(dp));
dp[1] = 0;
cin >> n;
for(int i = 1; i <= n; i ++)
{
cin >> a[i];
maxn = max(maxn, a[i]);
dp[1] += a[i];//全部1
}
ans = dp[1];//用1购买全部
for(int i = 1; i <= maxn; i ++)//用i来更新其他
{
for(int j = 2; j * i <= maxn; j ++)//枚举i的倍数
{
int chge = 0;//能用多少个大面额换
for(int r = 1; r <= n; r ++)
chge += a[r] / (i * j);
//每个节省j - 1张
//原先需要dp[i]个, 换成i * j的可以少(j - 1) * chge个
dp[i * j] = min(dp[i * j], dp[i] - (j - 1) * chge);
ans = min(ans, dp[i * j]);
}
}
printf("%d\n", ans);
}7.月之谜(acwing)

感觉数位DP实在克我,对大佬代码进行注释
AcWing 311. 月之谜 - AcWing
/*一个数的余数等于这个数的拆分的余数之和取余*/
/*如 5632 % p = (5000 % p + 600 % p + 30 % p + 2 % p) % p*/
/*所以在下面枚举的时候, 可以记录当前i位对p取余的余数,这样不影响正确性*/
#include <iostream>
#include<cstring>
#define int long long
using namespace std;
const int maxn = 100;
int f[30][maxn][maxn], num[maxn], p;
//f[i][j][k]表示前i个数,当前数位和为sum,且当前余数是k的方案数
int dfs(int u, int sum, int mod, bool limit)//pos为当前数位,sum为当前数位之和(p为枚举的数位之和),mod为当前余数,limit为上一位是否达到上限的标志
{
if(!u)//已经到了最后一位
{
if(sum == p && !mod) return 1;//如果枚举到了一个存在的数,且是月之数
return 0;
}
if(!limit && f[u][sum][mod] != -1) //当前数不超限且之前被计算过
return f[u][sum][mod];
int res = 0, up = limit ? num[u] : 9;//若上一位达到限制,当前位也有限制,否则 0 ~ 9 都可以填
for(int i = 0; i <= up; i ++)//枚举当前位填什么
{
//如果前几位都取到上限后一位必须取上限
res += dfs(u - 1, sum + i, (mod * 10 + i) % p, limit && i == up);
}
return limit ? res : f[u][sum][mod] = res;
}
int solve(int n)//计算1-n中满足条件的数(月之数)的个数
{
int cnt = 0;
while(n)
{
num[++ cnt] = n % 10;//每位数的上限
n /= 10;
}
int res = 0;
for(p = 1; p < maxn; p ++)//枚举所有可能数位之和 10 * 9 = 90
{
memset(f, -1,sizeof f);
res += dfs(cnt, 0, 0, 1);
}
return res;
}
signed main()
{
int l,r;
cin >> l >> r;
cout << solve(r) - solve(l - 1) << endl;
return 0;
}8.打鼹鼠(牛客)

用f[ i ] 表示从前 i 个鼹鼠中选的最大数列
能够转移等价于两个鼹鼠之间的距离 <= 后一个鼹鼠出现的时间 - 前一个鼹鼠出现的时间
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int f[N], n, m;
struct node
{
int t, x, y;
}mi[N];
bool check(int a, int b)
{
int t = mi[a].t - mi[b].t;
int w = abs(mi[a].x - mi[b].x) + abs(mi[a].y - mi[b].y);
return t >= w;
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= m; i ++)
{
int t, x, y;
scanf("%d%d%d", &t, &x, &y);
mi[i] = {t, x, y};
f[i] = 1;
for(int j = 1; j < i; j ++)
if(check(i, j)) f[i] = max(f[i], f[j] + 1);
}
int res = 0;
for(int i = 1; i <= m; i ++) res = max(res, f[i]);
cout << res << endl;
return 0;
}