题目

Meta-SR: A Magnification-Arbitrary Network for Super-Resolution
Meta-SR: 用于超分辨率的任何放大网络

摘要

由于DCNN的发展，最近关于超分辨率的研究取得了巨大成功。然而，任意比例因子的超分辨率长期以来一直被忽视。以往的研究者大多将不同比例因子的超分辨率视为独立的任务。他们为计算效率低下的每个比例因子训练一个特定的模型，而之前的工作只考虑了几个整数比例因子的超分辨率。在这项工作中，我们提出了一种称为Meta-SR的新方法，首先用单个模型解决任意比例因子（包括非整数）的超分辨率问题。在我们的Meta-SR中，提出了Meta-Upscale Module 来取代传统的upscale模块。对于任意比例因子，Meta-Upscale Module 通过将比例因子作为输入动态预测放大过滤器的权重，并使用这些权重生成任意大小的HR图像。对于任何低分辨率图像，我们的Meta-SR可以仅使用单个模型以任意比例因子连续放大图像。
我们通过对广泛使用的单图像超分辨率基准数据集进行大量实验来评估所提出的方法。实验结果显示了我们的Meta-Upscale的优越性。

引言

能否使用单一模型解决任意比例因子的超分辨率是一个重要的问题。然而，现有的大多数超分辨率方法仅考虑某些特定整数比例因子（$\times 2,\times 3,\times 4）$的超分辨率。这些方法将不同比例因子的超分辨率视为独立的任务。
例如，ESPCN、EDSR、RDN这些方法使用亚像素放大网络末端的特征图卷积。不幸的是，这些方法必须为每个比例因子设计一个特定的放大模块。每个放大模块只能以固定的整数比例因子，并且亚像素卷积仅适用于整数比例因子。这些缺点限制了超分辨率方法在真实场景中的使用。
受元学习的启发，我们提出了一个网络来动态预定义每个比例因子的过滤器权重。因此，我们不再需要为每个比例因子存储权重。与存储每个比例因子的权重相比，存储小权重网络预测网络更方便。

方法

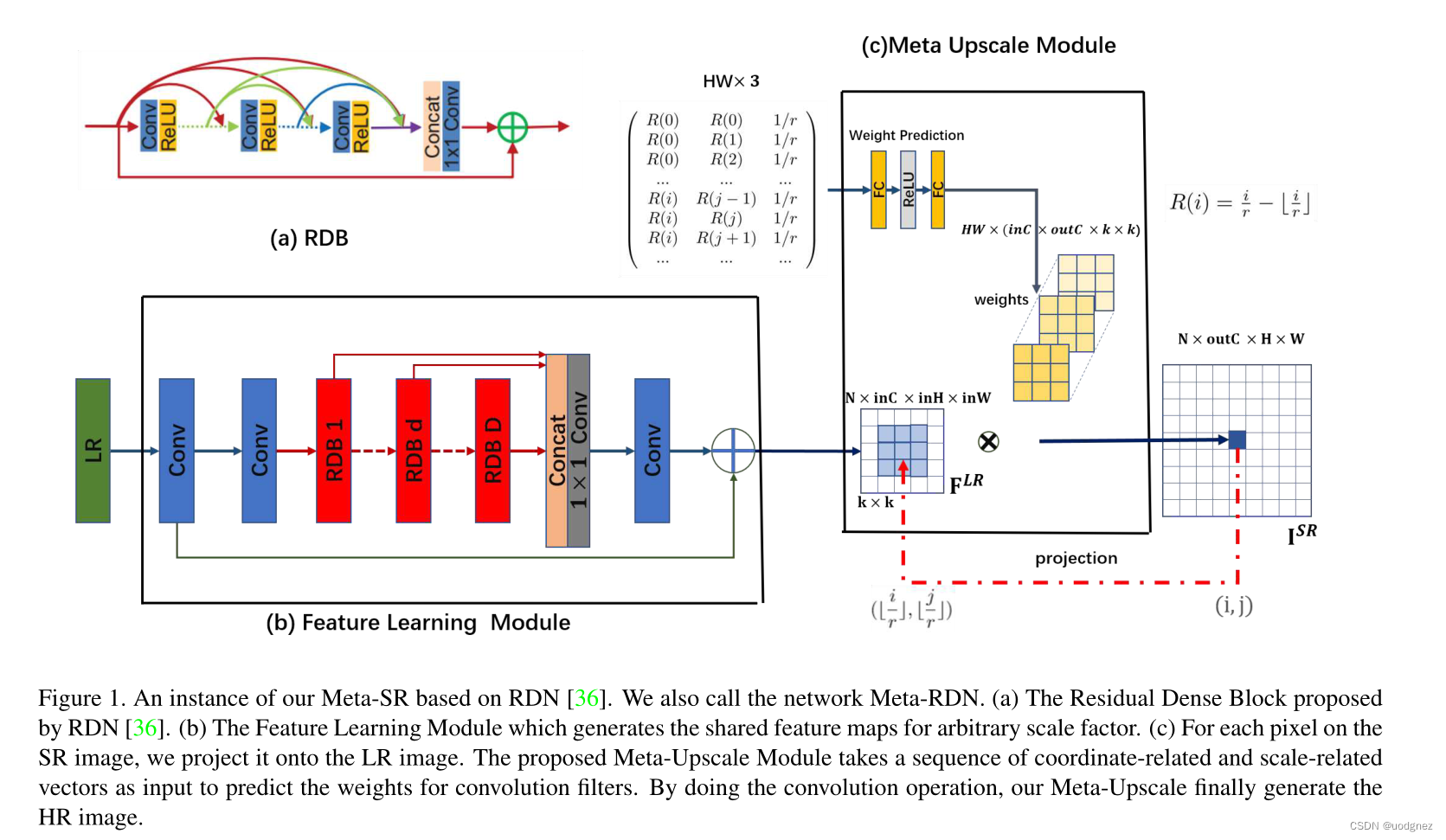
Meta-Upscale 规范

记 ${\mathbf{I}}^{SR}$ 为重建后的图像，${\mathbf{F}}^{LR}$ 表示特征学习模块提取到的特征，假设比例因子为 $r$。对于SR图像上的每个像素$(i,j)$，我们认为它是由LR图像上像素 $(i^{\prime },j^{\prime })$ 的特征和相应滤波器的权重决定的。从这个角度看，放大模块可以看作是映射 ${\mathbf{I}}^{SR}$ 和 ${\mathbf{F}}^{LR}$。首先，放大模块应该将像素 $(i,j)$ 映射到像素 $(i^{\prime },j^{\prime })$。然后，放大模板需要一个特定的滤波器来映射像素 $(i^{\prime },j^{\prime })$ 的特征，从而生成这个像素 $(i,j)$ 的值。数学描述为：
$${\mathbf{I}}^{SR}=\Phi ({\mathbf{F}}^{LR}(i^{\prime },j^{\prime }),\mathbf{W}(i,j))$$
由于SR图像上的每个像素对应一个滤波器。对于不同的比例因子，滤波器的数量和滤波器的权重都与另一个比例因子不同。为了解决单一模型对任意比例因子的超分辨率，我们提出了Meta-Upscale Module，根据比例因子和坐标信息动态预测权重 $\mathbf{W}(i,j)$。
对于Meta-Upscale Module，有三个重要的功能。即Location Projection 位置投影、Weight prediction 权重预测和 Feature Mapping 特征映射。如图所示：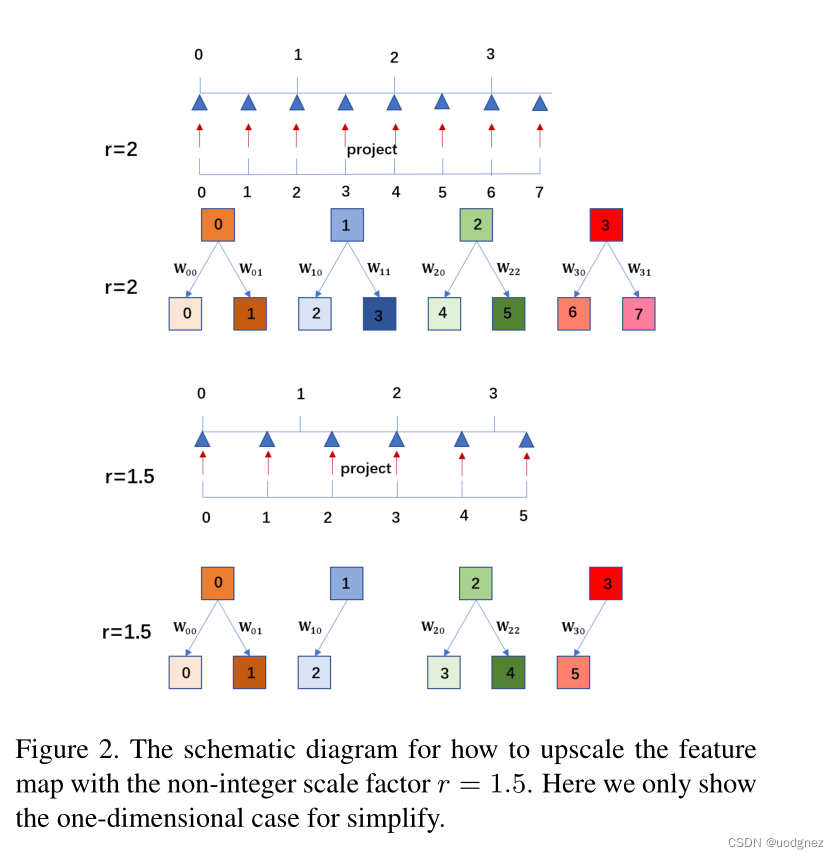
Location Projection 将像素投影到LR图像上； Weight Prediction 为SR图像上的每个像素预测滤波器的权重；最后，Feature Mapping 函数将LR图像上特征与预测的权重映射回SR图像，计算像素值。

Location Projection：对于SR图像上的每个像素点 $(i,j)$，位置投影就是找到LR图像上的 $(i^{\prime },j^{\prime })$。我们认为像素 $(i,j)$的值是由LR图像上的$(i^{\prime },j^{\prime })$的特征决定的。我们使用以下投影算子来映射这两个像素：
$$(i^{\prime },j^{\prime })=T(i,j)=(\lfloor \frac{i}{r}\rfloor ,\lfloor \frac{j}{r}\rfloor )$$
位置投影可以看作是一种可变分数步长机制，他可以使用任意比例因子放大特征图。如上图所示，如果比例因子为 $2$，则每个像素点$(i^{\prime },j^{\prime })$ 确定两个点。但是如果比例因子是非整数，比如 $r=1.5$，则有的像素决定2个像素，有的像素决定1个像素。对于SR图像上的每个像素 $(i,j)$，我们可以在LR图像上找到一个唯一的像素 $(i^{\prime },j^{\prime })$，我们认为这两个像素最相关。

Weight Prediction：对于典型的放大模块，它预先定义了每个比例因子的过滤器数量，并从训练集中学习 $\mathbf{W}$。不同的是，我们的Meta-Upscale Module 使用网络来预测过滤器的权重，公式化为：
$$\mathbf{W}(i,j)=\phi ({\mathbf{v}}_{ij};\theta )$$
对于像素 $(i,j)$ 的 $\phi (.)$输入，适当的选择是相当于 $(i^{\prime },j^{\prime })$的偏移量：
$${\mathbf{v}}_{ij}=(\frac{i}{r}-\lfloor \frac{i}{r}\rfloor ,\frac{j}{r}-\lfloor \frac{j}{r}\rfloor )$$
为了一起训练多个比例因子，最好将比例因子加到${\mathbf{v}}_{ij}$中以区分不同比例因子的权重。例如，如果我们想用比例因子2和4对图像进行放大，我们将它们分别表示为$I_2^{SR}$和$I_4^{SR}$。$I_2^{SR}$上的像素 $(i,j)$与 $I_4^{SR}$上的像素$(2i,2j)$具有相同的滤波器权重和相同的投影坐标。这意味着$I_2^{SR}$是$I_4^{SR}$的子图像。它会影响性能。因此我们将${\mathbf{v}}_{ij}$重新定义为：
$$$${\mathbf{v}}_{ij}=(\frac{i}{r}-\lfloor \frac{i}{r}\rfloor ,\frac{j}{r}-\lfloor \frac{j}{r}\rfloor ,\frac{1}{r})$$

Feature Mapping：我们从 ${\mathbf{F}}^{LR}$ 中提取LR图像上的 $(i^{\prime },j^{\prime })$的特征。我们用权重预测网络预测过滤器权重。我们需要做的最后一件事是将特征映射到SR图像上的像素值。我们选择矩阵积作为特征映射函数，如下：
$$\Phi ({\mathbf{F}}^{LR}(i^{\prime },j^{\prime }),\mathbf{W}(i,j))={\mathbf{F}}^{LR}(i^{\prime },j^{\prime })\mathbf{W}(i,j)$$

实验效果