自动驾驶决策规划算法

序章

课程链接：序章

第一章

（1）细说五次多项式

课程链接：五次多项式

参考一下这篇博客：

初始：位置，速度，加速度

终点：位置，速度，加速度。

边界条件就是六个初始条件，t = 0 时刻的，和t = t0的时刻状态，就可以求解这个五次多项式，得到一个x轴位置，速度，加速度关于t的方程。和y轴位置，速度，和加速度关于t的方程。

比较简单，只需要代入公式即可。

设一个五次多项式，分别对应的是x(t), y(t), v_x(t), v_y(t), a_x(t), a_y(t)

值得注意的一点是：五次多项式做轨迹规划，y不是关于x的曲线，而是y和x都是关于t的曲线。
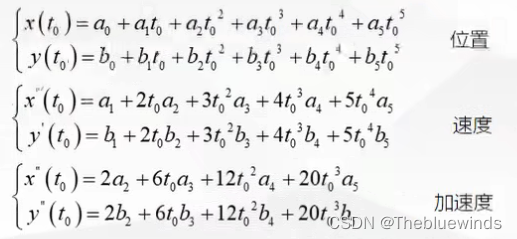
请添加图片描述

写为矩阵形势就是：

请添加图片描述

目前我们已知的信息是t0时刻的位置、速度和加速度。以及T终点时刻的根据这个初始t = 0的条件, 代入方程，可以求出a0，a1，和a2.

然后根据T时刻的位置，速度和加速度，代入方程中，可以求得剩下的a3，a4，a5.具体计算如下所示，(这里用横向求解来举例，纵向也是一样的过程)

t = 0的时刻，将初始条件代入方程得到的是：
$x\left( t_0 \right) =x\left( 0 \right) \,\,=\,\,x_s=a_0\,\, \\ x\prime\left( t_0 \right) \,\,=\,\,v_s\,\,=\,\,a_1 \\ x''\left( t_0 \right) \,\,=\,\,a_s\,\,=\,\,2*a_2$
这样可以求得三个方程组中的参数。然后是对T时刻的求解，将终点时刻的已知量代入到函数中，由于a0，a1，a2都是已知的了，我们将其移到左边，只构建右边a3，a4，a5三个未知量的矩阵来求解，首先代入后公式如下：
$x\left( t_T \right) =x\left( T \right) \,\,=\,\,x_g\,\,-\,\,a_0\,\,-a_1T\,\,-\,\,a_2T=\,\,a_3T^3\,\,+\,\,a_4T^4\,\,+\,\,a_5T^5 \\ x\prime\left( t_T \right) \,\,=\,\,v_g-a_1-2a_2T\,\,=\,\,3a_3T^2+4a_4T^3+5a_5T^4 \\ x''\left( t_T \right) \,\,=\,\,a_g-2*a_2\,\,=\,\,6a_3T\,\,+\,\,12a_4T^2+20a_5T^3$
利用python自带的np求解工具就可以求得剩余的a参数。写成矩阵形式很简单。

下面结合代码来写一下五次多项式的类。

# ########################################
# 构造一个五次多项式的类
class QuinticPolynomial:
    def __init__(self, xs, vxs, axs, xe, vxe, axe, time):
        # 起点条件代入进去得
        self.a0 = xs
        self.a1 = vxs
        self.a2 = axs / 2.0
        # 终点条件代入进去
        A = np.array([[time ** 3, time**4, time ** 5],
                      [3*time**2, 4*time**3, 5*time**4],
                      [6*time, 12*time**2, 20*time**3]])
        b = np.array([xe - self.a0 - self.a1*time - self.a2*time**2,
                      vxe - self.a1 - 2*self.a2*time,
                      axe - 2*self.a2])
        x = np.linalg.solve(A, b)
        self.a3 = x[0]
        self.a4 = x[1]
        self.a5 = x[2]

    def calc_point(self, t):  # 计算下一时刻t的位置。
        xt = self.a0 + self.a1 * t + self.a2 * t**2 + self.a3*t**3 + \
             self.a4 * t**4 + self.a5*t**5
        return xt

    def calc_first_derivative(self, t):  # 计算速度
        xt = self.a1 + 2* self.a2*t + 3*self.a3*t**2 + 4*self.a4*t**3 + 5*self.a5**4
        return xt

    def calc_second_derivative(self, t):  # 计算加速度
        xt = 2*self.a2 + 6*self.a3*t + 12*self.a4*t**2 + 20*self.a5*t**3
        return xt

    def calc_third_derivative(self, t):  # 返回jerk
        xt = 6*self.a3 + 24*self.a4*t + 60*self.a5*t**2
        return xt

完整代码如下：、

# 首先是输入的参数
import math
import matplotlib.pyplot as plt
import numpy as np
# ###########################################输入参数
MAX_T = 100.0  # 到达目标所需要的最大时间
MIN_T = 5.0  # 到达目标的最小时间

# 起点条件
sx = 10.0
sy = 10.0
syaw = np.deg2rad(10.0)
sv = 1.0
sa = 0.1

# 终点条件
gx = 30.0
gy = -10.0
gyaw = np.deg2rad(20.0)  # 终点的偏航角
gv = 1.0
ga = 0.1  # 加速度 m/ss

# 设置一个最大加速度与jerk
max_accel = 1.0
max_jerk = 0.5

# 时间间隔
dt = 0.1
# ########################################
# 构造一个五次多项式的类
class QuinticPolynomial:
    def __init__(self, xs, vxs, axs, xe, vxe, axe, time):
        # 起点条件代入进去得
        self.a0 = xs
        self.a1 = vxs
        self.a2 = axs / 2.0
        # 终点条件代入进去
        A = np.array([[time ** 3, time**4, time ** 5],
                      [3*time**2, 4*time**3, 5*time**4],
                      [6*time, 12*time**2, 20*time**3]])
        b = np.array([xe - self.a0 - self.a1*time - self.a2*time**2,
                      vxe - self.a1 - 2*self.a2*time,
                      axe - 2*self.a2])
        x = np.linalg.solve(A, b)
        self.a3 = x[0]
        self.a4 = x[1]
        self.a5 = x[2]

    def calc_point(self, t):  # 计算下一时刻t的位置。
        xt = self.a0 + self.a1 * t + self.a2 * t**2 + self.a3*t**3 + \
             self.a4 * t**4 + self.a5*t**5
        return xt

    def calc_first_derivative(self, t):  # 计算速度
        xt = self.a1 + 2* self.a2*t + 3*self.a3*t**2 + 4*self.a4*t**3 + 5*self.a5**4
        return xt

    def calc_second_derivative(self, t):  # 计算加速度
        xt = 2*self.a2 + 6*self.a3*t + 12*self.a4*t**2 + 20*self.a5*t**3
        return xt

    def calc_third_derivative(self, t):  # 返回jerk
        xt = 6*self.a3 + 24*self.a4*t + 60*self.a5*t**2
        return xt


# #######################################
# 构造五次多项式
# 计算出时间、空间、速度、加速度和jerk的信息

def quintic_polynomials_planner(sx, sy, syaw, sv, sa, gx, gy, gyaw, gv, ga, max_accel, max_jerk, dt):
    """
    :param sx:
    :param sy:
    :param syaw:
    :param sv:
    :param sa:
    :param gx:
    :param gy:
    :param gyaw:
    :param gv:
    :param ga:
    :param max_accel:
    :param max_jerk:
    :param dt:
    :return: time: time result
    rx : x position result list
    ry : y position result list
    ryaw : yaw angle result list
    rv: velocity result list
    ra: accel result list
    """
    # 将起点和终点速度进行横纵向解耦 注意：s代表起始位置，g代表目标位置
    vxs = sv * math.cos(syaw)
    vys = sv * math.sin(syaw)
    vxg = gv * math.cos(gyaw)
    vyg = gv * math.sin(gyaw)

    # 加速度解耦
    axs = sa * math.cos(syaw)
    ays = sa * math.sin(syaw)
    axg = ga * math.cos(gyaw)
    ayg = ga * math.sin(gyaw)

    # 创建一个计算求得的参考信息列表：
    time, rx, ry, ryaw, rv, ra, rj = [], [], [], [], [], [], []
    # np.arrange(a, b, c)有三个参数的时候，a是起点，b是终点，c是代表步长,生成一个列表
    # MINT是5，计算未来5个时间步的数据。
    # 枚举不同时间，生成对应的多项式轨迹。
    for T in np.arange(MIN_T, MAX_T, MIN_T): # 从最短的时间到最长的时间
        xqp = QuinticPolynomial(sx, vxs, axs, gx, vxg, axg, T)  # 横向五次多项式类对象
        yqp = QuinticPolynomial(sy, vys, ays, gy, vyg, ayg, T)  # 纵向
        time, rx, ry, ryaw, rv, ra, rj = [], [], [], [], [], [], []
        for t in np.arange(0.0, T+dt, dt):  # 枚举时间步长
            time.append(t)
            rx.append(xqp.calc_point(t))
            ry.append(yqp.calc_point(t))

            vx = xqp.calc_first_derivative(t)
            vy = yqp.calc_first_derivative(t)  # 未来dt时刻的坐标
            v = np.hypot(vx, vy)
            # v就是将vx和vy进行合成
            rv.append(v)

            yaw = math.atan2(vy, vx)
            ryaw.append(yaw)

            ax = xqp.calc_second_derivative(t)
            ay = yqp.calc_second_derivative(t)
            a = np.hypot(ax, ay)
            if len(rv) >=2 and rv[-1] - rv[-2] < 0.0:  # 如果速度开始下降，这里加速度需要取反。
                a *= -1
            # 说明在减速
            ra.append(a)

            jx = xqp.calc_third_derivative(t)  # 计算jerk
            jy = yqp.calc_third_derivative(t)  # 计算y方向的
            j = np.hypot(jx, jy)
            if len(ra) >= 2 and ra[-1] - ra[-2] < 0.0:  # 将加速度开始下降，jerk需要取反
                j *= -1
            rj.append(j)
        if max([abs(i) for i in ra]) <= max_accel and max([abs(i) for i in rj]) <= max_jerk:
            print("find path!!")
            break
    return time, rx, ry, ryaw, rv, ra, rj


time, rx, ry, ryaw, rv, ra, rj = quintic_polynomials_planner(
        sx, sy, syaw, sv, sa, gx, gy, gyaw, gv, ga, max_accel, max_jerk, dt)

# 绘制路径图
plt.subplots(1)
plt.plot(sx, sy, "or", label="Start")
plt.plot(gx, gy, "ob", label="Goal")
plt.plot(rx, ry, "-k", label="Path")
plt.grid(True)
plt.axis("equal")
plt.xlabel("x[m]")
plt.ylabel("y[m]")
plt.legend()

# 绘制速度曲线
plt.subplots(1)
plt.plot(time, rv, "-r", label="velocity")
plt.grid(True)
plt.xlabel("Time [s]")
plt.ylabel("Velocity [m/s]")
plt.legend()

plt.show()

（2）凸优化与非凸优化

课程链接：优化

大纲：

本节主要引出了参考线，还有约束问题，其次是代价。

首先来回顾一下规划总体流程：(已经得到了导航路径，需要决策 + 运动规划)

定位和导航：生成参考线坐标
分情况：
- 无障碍物：跟踪参考线路径
- 有静态障碍物：静态障碍物投影到SL图上(Frenet)
决策算法：对障碍物进行决策，决定是左避，还有右避，或者忽略。(开辟最优凸空间)
规划算法：在凸空间中搜索出来最优的路径。
后续处理：在规划轨迹中选取一个点，坐标转化为笛卡尔坐标系，输出给控制模块去控制即可。

从上述流程可以了解到首先需要解决的是参考线问题。接下来讲解一下参考线。

参考线：

目标：

解决导航的路径过长，不平滑的问题，通常从导航中获取到的全局路径都是由一段一段的线段构成，比较粗略，因此需要利用参考线实现平滑的操作。
路径太长，不方便找匹配点，搜索空间太大，也就是不利于坐标变换。

实现方案：每一个规划周期中，找到车在导航路径上的投影点，然后以投影点为坐标原点，往后取30米长度，往前取150米范围内的点，来做平滑，平滑后的点的集合称之为参考线。

具体实现：平滑算法。

利用三个点来找平滑的关系，然后简历一个二次规划来找到一个最优解。计算平滑代价，找到最小的。

(3) 直角坐标与自然坐标转换(上, 下)

课程链接：坐标变换1，坐标变换2

这一节内容主要看这三个博客：

第一节

第二节

第三节

具体内容如下：

通过第一节的计算，我们得出来一个Cartesian坐标系转化到Frenet坐标系的步骤：

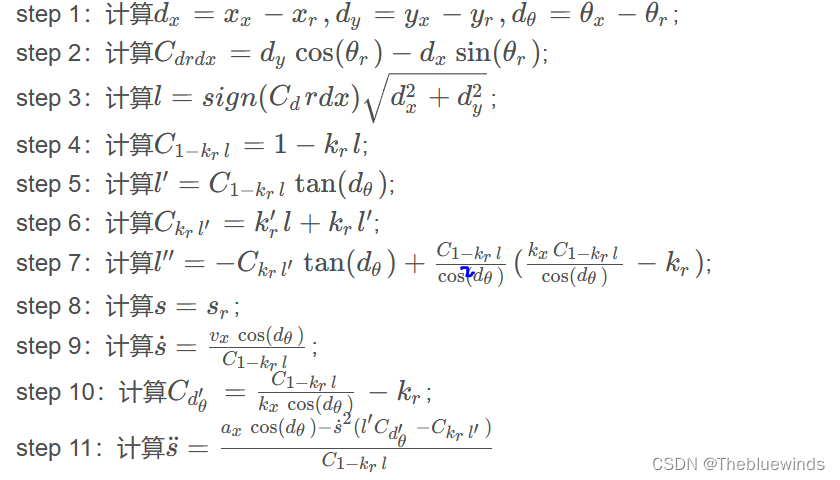
请添加图片描述

对应的python代码如下：

import numpy as np
from math import *

# 本函数是将Cartesian坐标系，转化为Frenet坐标系
# rs是参考点的frenet坐标纵向位置
# 已知(x_x,y_x,theta_x, v_x, a_x, k_x) 和 参考点(s_r, x_r, y_r, theta_r, v_r, a_r, k_r, d_kr)
# 待求：(六个参数) s, s_dot, s_dot_dot, l, l_pie, l_pie_pie.
def cartesian_to_frenet1D(rs, rx, ry, rtheta, rkappa, rdkappa, x, y, v, a, theta, kappa):
    # 创建一个numpy数组， 长度为3，初始值为0. s代表纵向的三个参数，位置，速度，加速度。 d代表横向三个参数
    s_condition = np.zeros(3)
    d_condition = np.zeros(3)

    dx = x - rx
    dy = y - ry

    cos_theta_r = cos(rtheta)
    sin_theta_r = sin(rtheta)

    cross_rd_nd = cos_theta_r*dy - sin_theta_r*dx  # 计算第二步，朝向C参数
    s_condition[0] = rs  # s
    # 第三步
    d_condition[0] = copysign(sqrt(dx*dx+dy*dy), cross_rd_nd)  # copysign(x, y)返回一个基于x绝对值和基于y符号的数值。x * y
    # 第四步
    delta_theta = theta - rtheta  # 角度差
    tan_delta_theta = tan(delta_theta)
    cos_delta_theta = cos(delta_theta)
    one_minis_kappa_r_d = 1 - rkappa * d_condition[0]  # C_drdx参数, 上面计算的d_condition[0]是横向误差d，也就是l
    # 第五步
    d_condition[1] = one_minis_kappa_r_d * tan_delta_theta
    # 第六步
    kappa_r_d_prime = rdkappa * d_condition[0] + rkappa * d_condition[1]
    # 第七步：计算l_pie_pie
    d_condition[2] = (-kappa_r_d_prime) * tan_delta_theta + one_minis_kappa_r_d / cos_delta_theta / cos_delta_theta *\
                     (kappa*one_minis_kappa_r_d / cos_delta_theta - rkappa)

    # 第八步：计算纵向位置s
    s_condition[0] = rs
    # 第九步：s_dot
    s_condition[1] = v * cos_delta_theta / one_minis_kappa_r_d
    # 第十步：计算参数C_dtheta
    delta_theta_prime = one_minis_kappa_r_d / kappa / cos_delta_theta - rkappa
    # 第十一步：计算s_dot_dot
    s_condition[2] = (a * cos_delta_theta - s_condition[1]* s_condition[1] * (d_condition[1] * delta_theta_prime - kappa_r_d_prime)) / (one_minis_kappa_r_d)

    return s_condition, d_condition

接下来是对Frenet坐标系转化为全局坐标系

请添加图片描述

代码如下：

def frenet_to_cartesian(rs, rx, ry, rtheta, rkappa, rdkappa, s_condition, d_condition):
    if fabs(rs - s_condition[0]) >= 1.0e-6:
        print("The reference point s and s_condition[0] don't match.")  # 说明参考点距离车辆太远了。
    cos_theta_r = cos(rtheta)
    sin_theta_r = sin(rtheta)
    # 第一步和第二步：计算x，y坐标
    x = rx - d_condition[0] * sin_theta_r
    y = ry + d_condition[0] * cos_theta_r
    # 中间参数
    one_minus_kappa_r_d  = 1 - rkappa*d_condition[0]
    tan_delta_theta = d_condition[1] / one_minus_kappa_r_d
    # 第四步计算角度
    delta_theta = atan2(tan_delta_theta, one_minus_kappa_r_d)  # d_theta
    theta = NormalizeAngle(delta_theta + rtheta)
    # 第五步:计算速度
    d_dot = d_condition[1] * s_condition[1]
    v = sqrt(one_minus_kappa_r_d * one_minus_kappa_r_d * s_condition[1]*s_condition[1] + d_dot * d_dot)
    # 第六步，计算角度
    cos_delta_theta = cos(delta_theta)
    # 第七步，计算C_kr_l参数
    kappa_r_d_prime = rdkappa * d_condition[0] + rkappa * d_condition[1]
    # 第八步：计算kx
    kappa = ((d_condition[2] + kappa_r_d_prime*tan_delta_theta) * cos_delta_theta * cos_delta_theta/one_minus_kappa_r_d + rkappa) \
            * cos_delta_theta / one_minus_kappa_r_d

    # 第九步：计算a
    a = s_condition[2] * (one_minus_kappa_r_d / cos_delta_theta) + (s_condition[1] * s_condition[1] / cos_delta_theta)* \
        (d_condition[1] * (kappa*one_minus_kappa_r_d/cos_delta_theta - rkappa) - kappa_r_d_prime)

    return x, y, v, a, theta, kappa