文章目录
- 前言
- 一 密码学
- 1.1 古典密码学
- 1.1.1 替换法
- 1.1.2 移位法
- 1.1.3 古典密码破解方式
- 二 近代密码学
- 2.1 现代密码学
- 2.1.1 散列函数
- 2.1.2 对称密码
- 2.1.3 非对称密码
- 二 凯撒加密的实践
- 2.1 基础知识:ASCII编码
- 2.2 ascii编码演示
- 2.3 凯撒加密和解密实践
- 2.4 频率分析解密法

前言
- 本文章学自尚硅谷密码学课程,面对小白群体!!!
- 本文章仅用于学习和交流,禁止用于其他用途,如若存在侵权,请及时联系作者,作者会及时进行处理。
一 密码学
- 密码学是研究编制密码和破译密码的技术科学。研究密码变化的客观规律,应用于编制密码以保守通信秘密的,称为编码学;应用于破译密码以获取通信情报的,称为破译学,总称密码学。
- 密码学是网络安全、信息安全、区块链等产品的基础,常见的非对称加密、对称加密、散列函数等,都属于密码学范畴。
- 密码学有数千年的历史,从最开始的替换法到如今的非对称加密算法,经历了古典密码学,近代密码学和现代密码学三个阶段。 密码学不仅仅是数学家们的智慧,更是如今网络空间安全的重要基础。
1.1 古典密码学
- 在古代的战争中,多见使用隐藏信息的方式保护重要的通信资料。但藏信息的方式比较容易被他人识破。通俗来讲,就是加密的方式相对来所比较简单。
1.1.1 替换法
- 替换法:用固定的信息将原文替换成无法直接阅读的密文信息。例如将 b 替换成 w ,e 替换成p ,这样bee 单词就变换成了wpp,不知道替换规则的人就无法阅读出原文的含义。
- 替换法有单表替换和多表替换两种形式。
- 单表替换即只有一张原文密文对照表单,发送者和接收者用这张表单来加密解密。如:表单为:
a b c d e - s w t r p。 - 多表替换即有多张原文密文对照表单,不同字母可以用不同表单的内容替换。
- 例如约定好表单为:表单 1:
a b c d e - s w t r p、表单2:a b c d e - c h f h k、表单 3:a b c d e - j f t o u。规定第一个字母用第三张表单,第二个字母用第一张表单,第三个字母用第二张表单,这时 bee单词就变成了(312)fpk,破解难度更高,其中 312 312 312 又叫做密钥,密钥可以事先约定好,也可以在传输过程中标记出来。
- 例如约定好表单为:表单 1:
1.1.2 移位法
- 移位法就是将原文中的所有字母都在字母表上向后(或向前)按照一个固定数目进行偏移后得出密文,典型的移位法应用有 “ 恺撒密码 ”
- 例如约定好向后移动2位(abcde - cdefg),这样 bee 单词就变换成了dgg 。
- 移位法也可以采用多表移位的方式 ,典型的多表案例是“维尼吉亚密码”(又译维热纳尔密码),属于多表密码的一种形式。

1.1.3 古典密码破解方式
- 古典密码虽然很简单,但在密码史上是使用的最久的加密方式,直到“概率论”的数学方法被发现,古典密码就被破解了。
- 在密码学中,频率分析是指研究字母或者字母组合在文本中出现的频率。应用频率分析可以破解古典密码。
- 频率分析基于如下原理:在任何一种书面语言中,不同的字母或字母组合出现的频率各不相同。而且,对于以这种语言书写的任意一段文本,都具有大致相同的特征字母分布。比如,在英语中,字母E出现的频率很高,而X则出现得较少。类似地,ST、NG、TH,以及QU等双字母组合出现的频率非常高,NZ、QJ组合则极少。英语中出现频率最高的12个字母可以简记为“ETAOIN SHRDLU”。
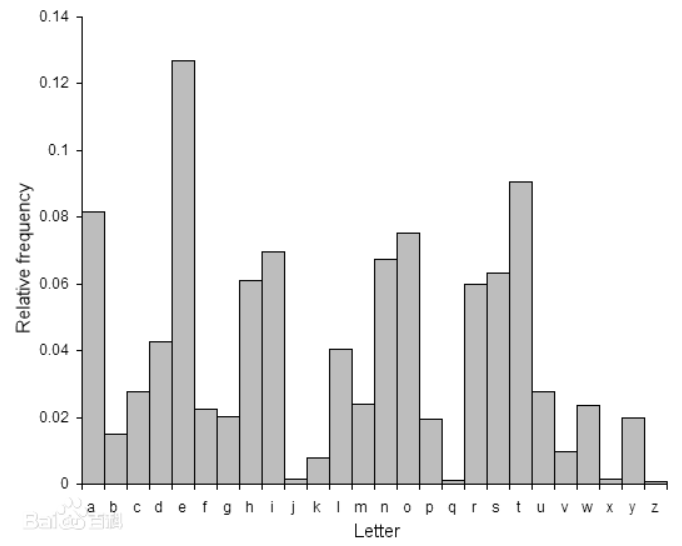
- 如果密文数量足够大,仅仅采用频度分析法就可以破解单表的替换法或移位法。
- 多表的替换法或移位法虽然难度高一些,但如果数据量足够大的话,也是可以破解的。以维尼吉亚密码算法为例,破解方法就是先找出密文中完全相同的字母串,猜测密钥长度,得到密钥长度后再把同组的密文放在一起,使用频率分析法破解。
二 近代密码学
- 恩尼格玛机是二战时期纳粹德国使用的加密机器,后被英国破译,参与破译的人员有被称为计算机科学之父、人工智能之父的图灵。
- 恩尼格玛机使用的加密方式本质上还是移位和替代,只不过因为密码表种类极多,破解难度高,同时加密解密机器化,使用便捷,因而在二战时期得以使用。

2.1 现代密码学
2.1.1 散列函数
- 散列函数【杂凑函数、摘要函数或哈希函数】,可将任意长度的消息经过运算,变成固定长度数值,常见的有MD5、SHA-1、SHA256,多应用在文件校验,数字签名中。
- MD5 可以将任意长度的原文生成一个128位(16字节)的哈希值
- SHA-1可以将任意长度的原文生成一个160位(20字节)的哈希值
2.1.2 对称密码
- 对称密码应用了相同的加密密钥和解密密钥。采用单钥密码系统的加密方法,也称为单密钥加密。
- 示例
- 现在有一个原文 3 3 3要发送给 B B B
- 设置密钥为 108 108 108, 3 ∗ 108 = 324 3 * 108 = 324 3∗108=324, 将 324 324 324作为密文发送给 B B B
- B拿到密文
324
324
324后, 使用
324
/
108
=
3
324/108 = 3
324/108=3 得到原文
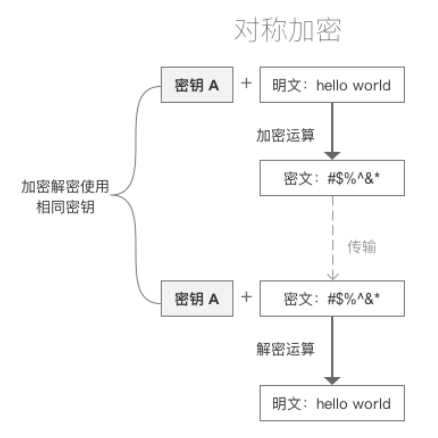
- 对称密码分为:序列密码(流密码),分组密码(块密码)两种。
- 流密码是对信息流中的每一个元素(一个字母或一个比特)作为基本的处理单元进行加密
- 如:原文为1234567890,流加密即先对1进行加密,再对2进行加密,再对3进行加密……最后拼接成密文;块加密先分成不同的块,
- 块密码是先对信息流分块,再对每一块分别加密。
- 如:1234成块,5678成块,90XX(XX为补位数字)成块,再分别对不同块进行加密,最后拼接成密文。前文提到的古典密码学加密方法,都属于流加密。
2.1.3 非对称密码
- 对称密码的密钥安全极其重要,加密者和解密者需要提前协商密钥,并各自确保密钥的安全性,一但密钥泄露,即使算法是安全的也无法保障原文信息的私密性。
- 在实际的使用中,远程的提前协商密钥不容易实现,即使协商好,在远程传输过程中也容易被他人获取,因此非对称密钥此时就凸显出了优势。
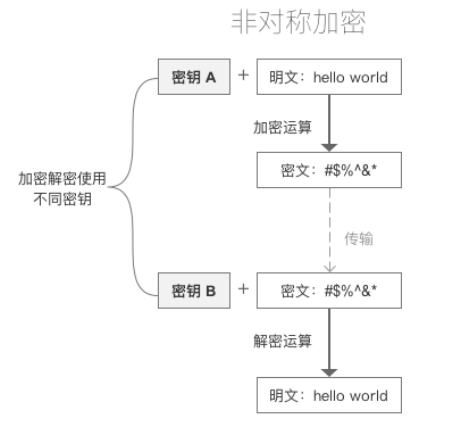
- 非对称密码有两支密钥,公钥(publickey)和私钥(privatekey),加密和解密运算使用的密钥不同。
- 用公钥对原文进行加密后,需要由私钥进行解密;用私钥对原文进行加密后(此时一般称为签名),需要由公钥进行解密(此时一般称为验签)。公钥可以公开的,大家使用公钥对信息进行加密,再发送给私钥的持有者,私钥持有者使用私钥对信息进行解密,获得信息原文。因为私钥只有单一人持有,因此不用担心被他人解密获取信息原文。
二 凯撒加密的实践
2.1 基础知识:ASCII编码
- ASCII(American Standard Code for Information Interchange,美国信息交换标准代码)是基于拉丁字母的一套电脑编码系统,主要用于显示现代英语和其他西欧语言。它是现今最通用的单字节编码系统,并等同于国际标准ISO/IEC 646。

2.2 ascii编码演示
-
依赖:
<dependencies> <dependency> <groupId>commons-io</groupId> <artifactId>commons-io</artifactId> <version>2.6</version> </dependency> </dependencies> -
字符串转换成ascii码
public class AsciiDemo { public static void main(String[] args) { // 定义字符串 String a = "AaZ"; // 需要拆开字符串 char[] chars = a.toCharArray(); for (char aChar : chars) { int asciicode = aChar; System.out.println(asciicode); } } }
2.3 凯撒加密和解密实践
- 在密码学中,恺撒密码是一种最简单且最广为人知的加密技术。恺撒密码通常被作为其他更复杂的加密方法中的一个步骤。
- 凯撒密码最早由古罗马军事统帅盖乌斯·尤利乌斯·凯撒在军队中用来传递加密信息,故称凯撒密码。这是一种位移加密方式,只对26个字母进行位移替换加密,规则简单,容易破解。下面是位移1次的对比:

- 字母表最多可以移动25位。凯撒密码的明文字母表向后或向前移动都是可以的,通常表述为向后移动,如果要向前移动1位,则等同于向后移动25位,位移选择为25即可。它是一种替换加密的技术,明文中的所有字母都在字母表上向后(或向前)按照一个固定数目进行偏移后被替换成密文。
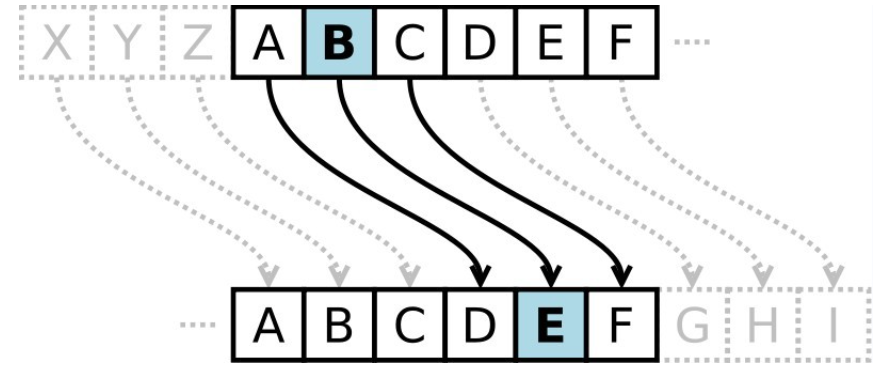
- 当秘钥为n,其中一个待加密字符ch,加密之后的字符为ch+n,当ch+n超过’z’时,回到’a’计数。
public class KaiserDemo {
public static void main(String[] args) {
// 定义原文
String input = "HELLO WORLD";
// 把原文右边移动3位
int key = 3;
// 凯撒加密
String s = encrypt(input,key);
System.out.println("加密==" + s);
String s1 = decrypt(s,key);
System.out.println("明文=="+s1);
}
/**
* 解密
* @param s 密文
* @param key 密钥
* @return
*/
public static String decrypt(String s, int key) {
char[] chars = s.toCharArray();
StringBuilder sb = new StringBuilder();
for (char aChar : chars) {
int b = aChar;
//记录加密后的字符
int temp=aChar;
// 偏移数据
b -= key;
//如果解码后,发生下溢,则将其+26
// 同时使用temp判断加密后的字符是否字母,是,进行下溢修正,否则,不做操作
if(b<'A' && temp>'A') {
b+=26;
}
char newb = (char) b;
sb.append(newb);
}
return sb.toString();
}
/**
* 加密
* @param input 原文
* @return
*/
public static String encrypt(String input,int key) {
// 把字符串变成字节数组
char[] chars = input.toCharArray();
StringBuilder sb = new StringBuilder();
for (char aChar : chars) {
int b = aChar;
// 往右边移动3位
b = b + key;
//控制大写字母的移位范围A-Z循环,超过范围从头开始
if(b>'Z'){
b-=26;
}
char newb = (char) b;
sb.append(newb);
}
return sb.toString();
}
}

2.4 频率分析解密法
- 以英文字母为例,为了确定每个英文字母的出现频率,分析一篇或者数篇普通的英文文章,英文字母出现频率最高的是e,接下来是t,然后是a……,然后检查要破解的密文,也将每个字母出现的频率整理出来,假设密文中出现频率最高的字母是j,那么就可能是e的替身,如果密码文中出现频率次高的但是P,那么可能是t的替身,以此类推便就能解开加密信息的内容。这就是频率分析法。
- 将明文字母的出现频率与密文字母的频率相比较的过程
- 通过分析每个符号出现的频率而轻易地破译代换式密码
- 在每种语言中,冗长的文章中的字母表现出一种可对之进行分辨的频率。
- e是英语中最常用的字母,其出现频率为八分之一
- 关键代码
/**
* 频率分析法破解凯撒密码
*/
public class FrequencyAnalysis {
//英文里出现次数最多的字符
private static final char MAGIC_CHAR = 'e';
//破解生成的最大文件数
private static final int DE_MAX_FILE = 4;
public static void main(String[] args) throws Exception {
printCharCount("src/article.txt");
//加密文件
int key = 3;
encryptFile("src/article.txt", "article_en.txt", key);
//测试1,统计字符个数
printCharCount("article_en.txt");
//读取加密后的文件
String artile = Util.file2String("article_en.txt");
//解密(会生成多个备选文件)
decryptCaesarCode(artile, "article_de.txt");
}
public static void printCharCount(String path) throws IOException{
String data = Util.file2String(path);
List<Entry<Character, Integer>> mapList = getMaxCountChar(data);
for (Entry<Character, Integer> entry : mapList) {
//输出前几位的统计信息
System.out.println("字符'" + entry.getKey() + "'出现" + entry.getValue() + "次");
}
}
public static void encryptFile(String srcFile, String destFile, int key) throws IOException {
String artile = Util.file2String(srcFile);
//加密文件
String encryptData = KaiserDemo.encrypt(artile, key);
//保存加密后的文件
Util.string2File(encryptData, destFile);
}
/**
* 破解凯撒密码
* @param input 数据源
* @return 返回解密后的数据
*/
public static void decryptCaesarCode(String input, String destPath) {
int deCount = 0;//当前解密生成的备选文件数
//获取出现频率最高的字符信息(出现次数越多越靠前)
List<Entry<Character, Integer>> mapList = getMaxCountChar(input);
for (Entry<Character, Integer> entry : mapList) {
//限制解密文件备选数
if (deCount >= DE_MAX_FILE) {
break;
}
//输出前几位的统计信息
System.out.println("字符'" + entry.getKey() + "'出现" + entry.getValue() + "次");
++deCount;
//出现次数最高的字符跟MAGIC_CHAR的偏移量即为秘钥
int key = entry.getKey() - MAGIC_CHAR;
System.out.println("猜测key = " + key + ", 解密生成第" + deCount + "个备选文件" + "\n");
String decrypt = KaiserDemo.decrypt(input, key);
String fileName = "de_" + deCount + destPath;
Util.string2File(decrypt, fileName);
}
}
//统计String里出现最多的字符
public static List<Entry<Character, Integer>> getMaxCountChar(String data) {
Map<Character, Integer> map = new HashMap<Character, Integer>();
char[] array = data.toCharArray();
for (char c : array) {
if(!map.containsKey(c)) {
map.put(c, 1);
}else{
Integer count = map.get(c);
map.put(c, count + 1);
}
}
//获取获取最大值
int maxCount = 0;
for (Entry<Character, Integer> entry : map.entrySet()) {
//不统计空格
if (/*entry.getKey() != ' ' && */entry.getValue() > maxCount) {
maxCount = entry.getValue();
}
}
//map转换成list便于排序
List<Entry<Character, Integer>> mapList = new ArrayList<Entry<Character,Integer>>(map.entrySet());
//根据字符出现次数排序
Collections.sort(mapList, new Comparator<Entry<Character, Integer>>(){
public int compare(Entry<Character, Integer> o1,
Entry<Character, Integer> o2) {
return o2.getValue().compareTo(o1.getValue());
}
});
return mapList;
}
}
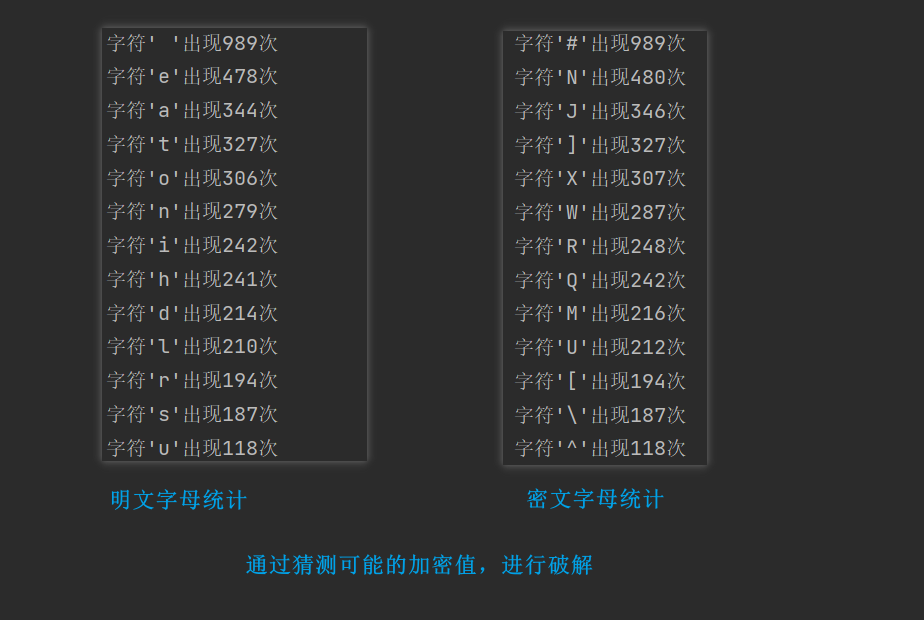

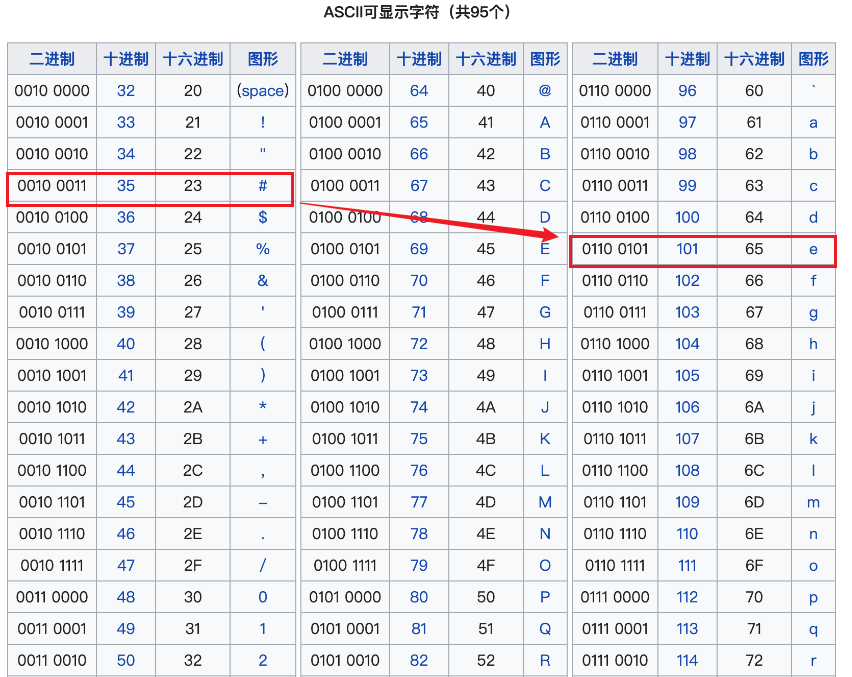
- 运行结果 # 出现次数最多, 我们知道在英文当中 e 出现的频率是最高的,我们假设现在 # 号,就是 e ,变形而来的 ,我以对照 ascii 编码表 ,凯撒加密当中位移是加了一个 key ,所以猜测两个值直接相差 -66 ,以 -66 进行解密 生成一个文件,查看第一个文件发现读不懂,所以解密失败。再猜测 h 是 e ,h 和 e 之间相差3 ,所以我们在去看第二个解密文件,发现可以读懂,解密成功。