198.打家劫舍

• 题目链接：代码随想录

• 解题思路：
  1.dp[i]：考虑下标i（包括i）以内的房屋，最多可以偷窃的金额为dp[i] 只是考虑，不一定偷
  2.递推公式：dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]),根据选不选i位置，由两个方面推导而来
  3.dp数组如何初始化。因为递推公式是dp[i-1]和dp[i-2]，所以初始化要考虑dp[0]和dp[1]
  因为要取最大值，所以dp[0] 一定是 nums[0]，dp[1]就是nums[0]和nums[1]的最大值即：dp[1] = max(nums[0], nums[1])
  4.遍历顺序：从前向后。因为后面状态由前面推出来

public int rob(int[] nums) {

    if(nums.length == 1){
        return nums[0];
    }

    //1.定义dp数组，dp数组表示dp[i]，考虑i位置的情况下能打劫到的最大价值
    //这里dp[i]中的i代表不一定选第i个位置的数字
    int[] dp = new int[nums.length];

    //2.初始化
    dp[0] = nums[0];
    dp[1] = Math.max(nums[0], nums[1]);
    //3.遍历
    for (int i = 2; i < dp.length; i++) {
        //根据选不选i位置的数值
        //选，只能加上dp[i-2]的数值
        dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
    }

    //4.最后返回递推的结果
    return dp[nums.length - 1];
}

213.打家劫舍II

关键点：将环形问题的情况分解成线性问题的情况，进而求解

• 题目链接：代码随想录

• 解题思路：
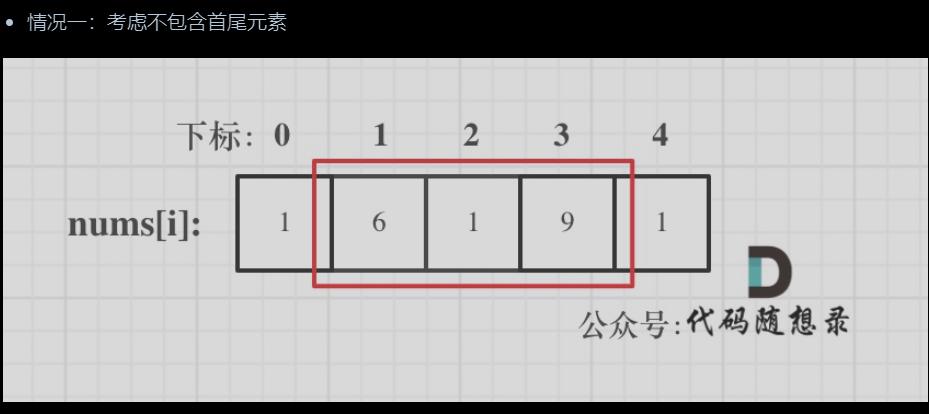
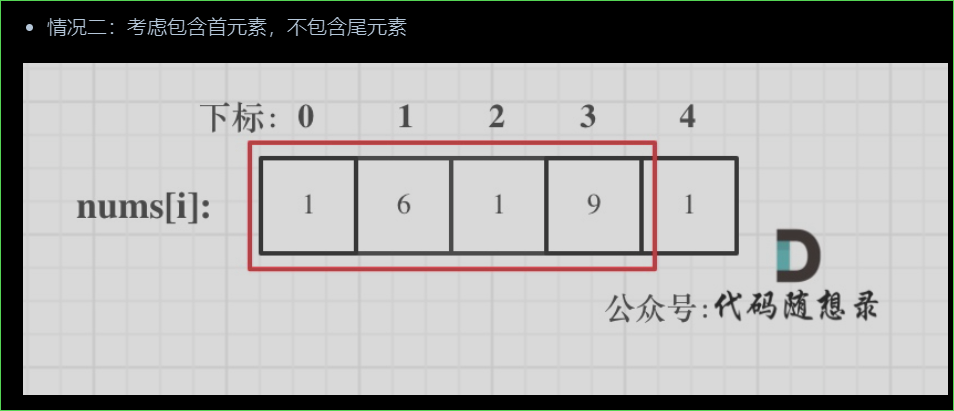
  ①根据环形问题，分为三种情况。一种不考虑首尾，一种考虑首不考虑尾，最后一种考虑尾不考虑首
  后两种情况考虑首不考虑尾就包含了不考虑首尾的问题，因此只用将最后两种打家劫舍问题求一个和即可
  ②编写一个有参数的打家劫舍函数，里面进行初始化和相应范围的打家劫舍问题的分析。
  要想编写容易，要借用自动扩容的ArrayList数组，dp范围和nums范围和位置一致

• 三种状态

  

public int rob(int[] nums) {
    int len = nums.length;
    //保证len从3开始
    if(len == 1){
        return nums[0];
    }
    if(len == 2){
        return Math.max(nums[0], nums[1]);
    }

    return Math.max(robAction(nums, 0, len - 2),robAction(nums, 1, len - 1));

}

/**
     * 考虑[start,end]位置房屋的打家劫舍问题
     * @param nums
     * @param start
     * @param end
     * @return
     */
private int robAction(int[] nums, int start, int end) {
    //定义dp数组的时候，要选用可扩容的ArrayList，因为要保证dp数组下标值和nums数组下标值一样
    List<Integer> dp = new ArrayList<>(nums.length);
    for(int i = 0;i < dp.size();i++){
        dp.add(0);
    }
    //初始化
    dp.set(start, nums[start]);
    dp.set(start + 1, Math.max(nums[start], nums[start + 1]));
    for (int i = start + 2; i <= end; i++) {
        dp.set(i, Math.max(dp.get(i - 2) + nums[i], dp.get(i - 1)));
    }

    return dp.get(end);
}
public static void main(String[] args) {
    List<Integer> dp = new ArrayList<>(2);
    System.out.println(dp.size());//0  这里只有首次添加元素之后，size1才变化
    dp.add(0, 0);
    System.out.println(dp.size());//1
}

337.打家劫舍III

本题是树形dp的入门级别的题目，通过返回dp数组来保存遍历状态 也称状态标记递归，通过一个标记，来记录遍历过程中的最大值

• 题目链接：代码随想录

• 解题思路：
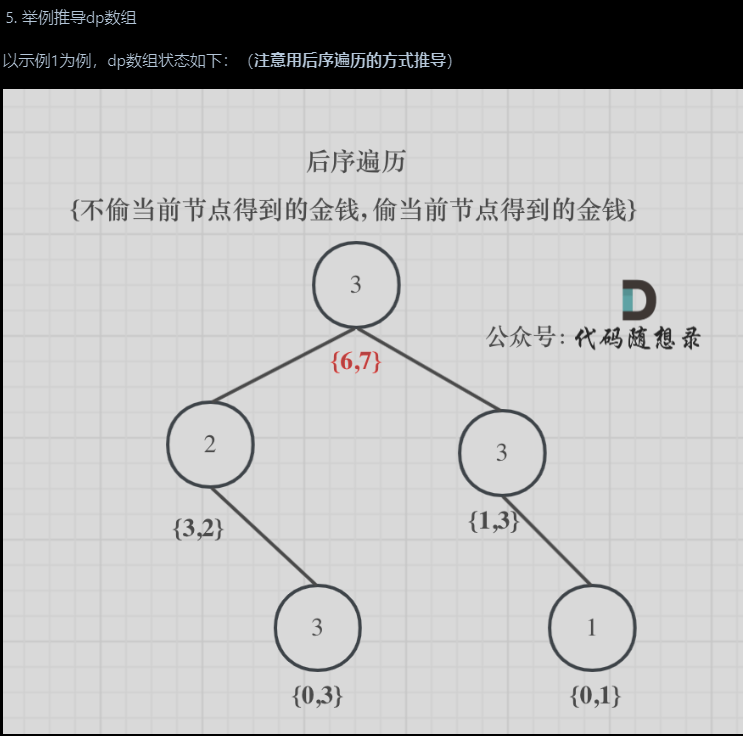
  1.确定递归函数的参数和返回值
  那么返回值就是一个长度为2的dp数组。dp[0]表示不偷当前节点情况下的金钱，dp[1]偷当前节点情况下的金钱，参数为当前节点，将当前节点偷与不偷得到的金钱返回给上一层
  在递归过程中，系统栈会保存每一层递归的参数，因此每一个节点的dp数组经过分析汇聚给root
  2.终止条件
  遇到空节点，直接返回本层偷的结果{0,0}
  3.确定遍历顺序：
  采用后序遍历，因为要根据左右节点的偷的金钱状态，根节点判断当前根偷还是不偷
  这种需要依靠状态的，都需要采取后序遍历
  4.确定单层递归逻辑：
  如果偷当前节点，那么dp[1] = root.val + 左右节点不偷的金钱
  如果不偷当前节点，那么左右节点可以偷，也可以不偷，因此dp[0] = max([0],[1])(左右节点)

• 推导过程:

  

public int rob(TreeNode root) {
    int[] dp = robAction1(root);

    return Math.max(dp[0], dp[1]);
}


/**
     * 递归树
     * @param root
     * @return 一个dp一维数组
     */
private int[] robAction1(TreeNode root){
    //本层dp状态数组
    int[] dp = new int[2];
    //终止条件
    if(root == null){
        return dp;
    }

    int[] leftDp = robAction1(root.left);
    int[] rightDp = robAction1(root.right);

    //本根不偷
    dp[0] = Math.max(leftDp[0], leftDp[1]) + Math.max(rightDp[0], rightDp[1]);
    //本根偷
    dp[1] = root.val + leftDp[0] + rightDp[0];

    //返回本层偷与不偷的状态
    return dp;
}