【小样本分割 2022 ECCV】SSP

论文题目：Self-Support Few-Shot Semantic Segmentation

中文题目：自支持小样本语义分割

论文链接：https://arxiv.org/abs/2207.11549

论文代码：https://github.com/fanq15/ssp

论文团队：香港科学技术大学&哈尔滨工业大学&快手科技

发表时间：2022年7月

DOI:

引用：Fan Q, Pei W, Tai Y W, et al. Self-support few-shot semantic segmentation[C]//Computer Vision–ECCV 2022: 17th European Conference, Tel Aviv, Israel, October 23–27, 2022, Proceedings, Part XIX. Cham: Springer Nature Switzerland, 2022: 701-719.

引用数：10【截止时间：2023年5月1号】

摘要

现有的基于支持-查询匹配框架的小样本分割方法取得了很大的进展。 但是他们仍然严重地受到了来自少量支持的类内变化的有限覆盖的影响。

基于简单格式塔原理，即同一对象的像素比同一类不同对象的像素更相似，我们提出了一种新的自支持匹配策略，

该策略使用查询原型来匹配查询特征，其中查询原型是从高置信度的查询预测中收集的。

该策略能够有效地捕获查询对象的一致底层特征，从而匹配查询特征。 提出了自适应的自支撑背景原型生成模块和自支撑损失，进一步方便了自支撑匹配过程。

我们的自支持网络大大提高了原型的质量，从更强的骨干和更多的支持中受益于更多的改进，并在多个数据集上实现了SOTA。

现有的一些小样本分割方法在支持-查询匹配框架的基础上取得了很大的进展。

• 存在的问题 : support和query同类目标之间存在的外观差异。
• 动机 : 基于简单格式塔原理，即属于同一目标的像素比属于同—类的不同目标的像素更相似。
• 本文贡献:
  • 提出了一种新的自支持匹配策略，该策略使用查询原型来匹配查询特征，其中查询原型是从高
    置信度查询预测中收集的。该策略可以有效地捕获查询目标的一致基本特征，从而匹配查询特征。
  • 还提出了自适应自支持背景原型生成模块和自支持损失，以进一步促进自支持匹配过程。本文
    自支持网络大大提高了原型质量，在多个数据集上实现了SOTA。

1. 介绍

语义分割已经在深度学习网络[29,42,34]和大规模数据集[15,5,93]中取得了显著的进展。 然而，目前高性能的语义分割方法严重依赖于费力的像素级标注，这加速了近年来小样本语义分割(FSS)的发展。

小样本语义分割的目的是只使用少量支持样本来分割任意新的类。 困难在于支持图像是有限的和固定的（通常每个类支持{1,3,5,10}），而查询图像可能是大量的和任意的。

无论支持质量如何，有限的支持图像很容易无法覆盖查询图像中目标类的潜在外观变化。 这显然是由固有的数据稀缺性和多样性造成的，这是小样本学习中两个长期存在的问题。

---

现有的方法试图通过充分利用有限的支持来解决这一问题，如提出更好的匹配机制或生成具有代表性的原型。 尽管它们取得了成功，但仍然不能从根本上解决有限镜头支撑下的外观差异问题。

但是这些方法都无法从根本上解决 support 和 query 之间的 appearance gap 问题。因为它们还都局限在利用非常少数的 support 去分割无穷的 query。

---

我们提出了一种新的自支持匹配策略来缩小匹配外观差异。 这种策略使用查询原型来匹配查询特性，或者换句话说，使用查询特性来自我支持。 因此，由于查询原型的自匹配特性，我们将其称为自支持原型。 这个新想法的动机是经典格式塔定律，即属于同一物体的像素比属于不同物体的像素更相似。

---

请参阅图1，以获得对我们新颖的自我支持匹配的高级理解。 首先，通过直接匹配支持原型和查询特征生成初始掩码预测。 在初始查询掩码的基础上，收集可信的查询特征生成自支持原型，用于与查询特征进行匹配。 我们的自我支持模块(SSM)收集猫头的可靠特征，用于分割整个黑猫。 我们的模型在基类上进行了优化，以检索由对象片段支持的其他对象部分，即自支持原型。

---

我们将我们的自支持模块应用于前景和背景原型中进行自支持匹配。 虽然SSM直接有利于前景原型，但请注意，背景通常是杂乱的，这不具有所有背景像素之间共享的全局语义共同性。

因此，我们不是通过聚集所有背景像素来生成全局背景原型，而是通过动态聚集查询图像中相似的背景像素来自适应地为每个查询像素生成自我支持的背景原型。

自适应支持背景原型(ASBP)是由独立的背景区域具有局部语义相似性这一事实所驱动的。 最后，我们提出了一个自支撑损失(SSL)来进一步方便自支撑程序。

---

因此，我们的自支持匹配策略与传统的支持-查询匹配有根本的不同。 采用灵活的自支持原型进行查询特征匹配，可以有效地捕捉查询对象的一致底层特征，从而实现对查询特征的匹配。 如图1所示，查询和支持图像中的猫在颜色、部位和尺度上都有很大差异，加菲猫支持图像与黑猫查询图像有很大的外观差异，传统的支持-查询匹配无疑会产生较差的分割。 在我们的自支持匹配中，我们的自支持原型（黑猫头部）与查询（整个黑猫）更加一致，因此我们的方法得到了令人满意的结果。

---

我们是第一个在查询原型和查询特征之间执行自我支持匹配的。 如图1所示，我们的自支撑匹配从根本上不同于常规匹配。 其他方法从额外的未标记图像(PPNET[57]和MLC[82])中学习用于支持查询匹配的更好的支持原型，或者基于支持图像构建各种支持原型生成模块[71，45，81]或特征先验(PFENET[73])。 虽然Panet[75]和CRNET[55]也探索了查询原型，但它们使用查询原型来匹配支持特征，仅作为辅助训练的查询-支持匹配，不能解决外观差异问题。

我们的自支持方法通过缓解类内外观差异问题显著提高了原型质量，在我们的实验验证中，在多个数据集上的性能提升证明了这一点。 尽管思想简单，但我们的自支持方法非常有效，具有多种优点，如更强的主干和更多的支持，产生高置信度的预测，对弱支持标签的鲁棒性更强，对其他方法的泛化程度更高，运行效率更高。 我们将用深入的实验来证实这些优点。 概括地说，我们的贡献是：

• 提出了一种新的自支持匹配方法，并构造了一种新的自支持网络来解决FSS中的外观差异问题。
• 我们提出了自我支持原型，自适应自我支持背景原型和自我支持损失，以方便我们的自我支持方法。
• 我们的自我支持方法从更强大的骨干和更多的支持中受益更多的改进，并在多个数据集上优于以前的SOTA，具有许多可取的优势。

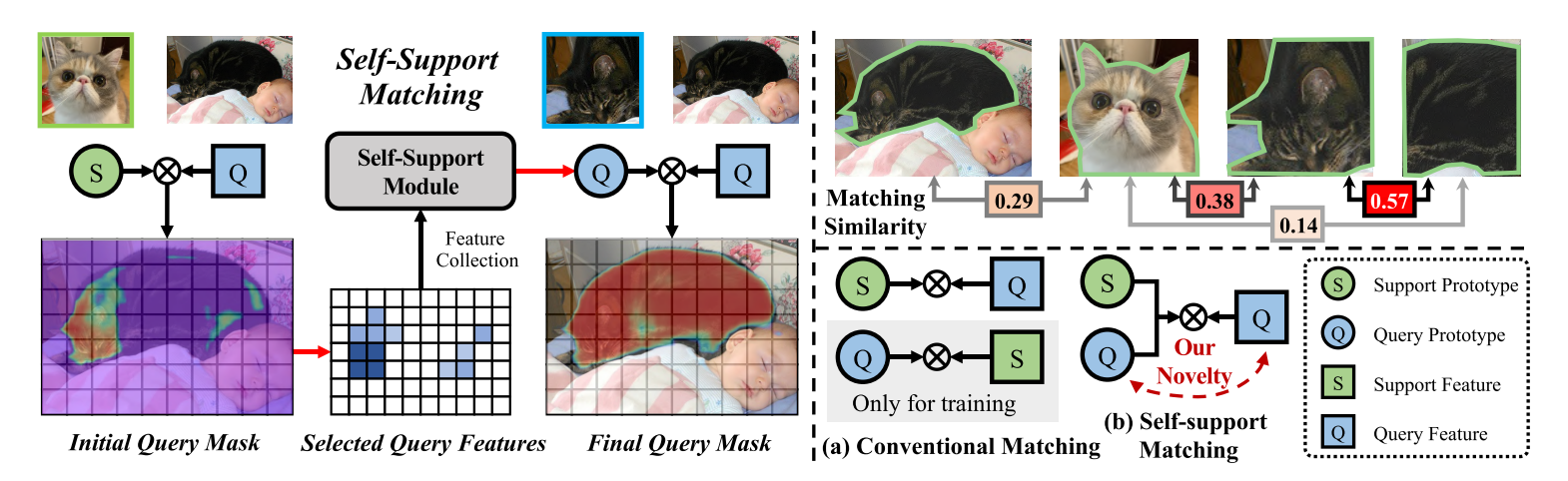
左图说明了我们自支持匹配的核心思想。利用初始查询掩码预测在高置信度区域收集查询特征，然后利用生成的查询原型与查询特征进行自匹配。

右上方的图像说明了我们自我支持匹配的动机：相同对象的像素/区域比来自不同对象的像素/区域更相似。 方框中的数字表示两个物体之间的余弦相似度。

右下角的图像说明了我们的自我支持匹配与传统的匹配方法有根本的不同。

语义分割在深度学习网络和大规模数据集方面取得了显著进展。但是当前高性能语义分割方法严重依赖于费力的像素级标注，加速了小样本语义分割(FSS)的发展。

FSS的问题: 固有的数据稀少性和数据多样性

• 数据稀少性是指支持图像很少，每个新类别只有不到10个样本。
• 数据多样性是指查询图像可能是海量和任意的。

支持图像中物体根本无法涵盖所有查询图像中同类别物体。

2. 相关工作

语义分割。

语义分割是计算机视觉的一个基本任务，用于产生像素级的稠密语义预测。 端到端的全卷积网络(FCN)[58]极大地推进了这一技术的发展。 随后的工作遵循了FCN范式，并贡献了许多有效的模块来进一步提高性能，如编码器-解码器体系结构[4,13,11,67]、图像和特征金字塔模块[39,91,10,49,50]、上下文聚合模块[25,26,33,92,95,36,85,89]和高级卷积层[84,9,14,63]。 尽管如此，上述分割方法在很大程度上依赖于丰富的像素级标注。 本文旨在解决少镜头场景下的语义分割问题。

小样本学习。

小样本学习的目标是从很少的样本中识别新的概念。 在过去的几年里，这种低成本的财产吸引了许多研究兴趣。 主要有三种方法。 第一种是迁移学习方法[12，28，16，65]，通过在两个阶段的优化过程中将从基类学习到的先验知识调整到新的类。 第二种是基于优化的方法[24,6,44,30,43,2,31,68]，它通过从少量样本中元学习优化过程来快速更新模型。 最后是基于度量的方法[1,17,35,40,46,47]，它在支持查询对上应用暹罗网络[40]来学习评估它们相关性的一般度量。 我们的工作，包括许多关于各种高级计算机视觉任务的少量工作[23，37，90，80，22]都受到了基于度量的方法的启发。

小样本语义分割。

小样本语义分割是Shaban等人首创的。 [69]。 后来的工作主要采用了基于度量的主流范式[18]，并进行了各种改进，例如用各种注意机制[70，54，83]、更好的优化[94，53]、存储模块[77，79]、图神经网络[78，74，87]、基于学习的分类器[72，59]、渐进匹配[32，96]或其他高级技术[86，52，61，48]改进支持查询图像之间的匹配过程。 我们是第一个在查询原型和查询特征之间执行自我支持匹配的。 我们的自支持匹配方法也与原型生成方法有关。 有些方法利用额外的未标记数据[82,57]或特征先验信息[73]来进一步增强特征。 其他方法使用各种技术生成代表性支持原型，例如，注意机制[88，27]、自适应原型学习[71，45，64]或各种原型生成方法[62，81]。 尽管查询原型已经在一些方法中得到了探索[75，55]，但它们只使用查询原型来匹配支持特征以进行原型正则化。 最后，现有方法在支持-查询匹配中存在类内差异问题。 另一方面，我们提出了一种新的自我支持匹配策略来有效地解决这个匹配问题。

3. 自支持小样本语义分割

在只有少量支持图像的情况下，小样本语义分割的目的是利用从基类中推广的模型来分割新类的对象。 现有主流的少镜头语义分割方案可表述为：输入支持和查询图像 { I s , I q } \left\{I_{s},I_{q}\right\} {Is​,Iq​}通过权重共享主干处理，提取图像特征 { F s , F q } ∈ R C × H × W , \{\mathcal{F}_{s},\mathcal{F}_{q}\}\in\mathbb{R}^{C\times H\times W}, {Fs​,Fq​}∈RC×H×W,,其中C为通道大小，H×W为特征空间大小。 然后将支持度特征${\mathcal{F}}_s$及其地真掩码${\mathcal{M}}_s$送入掩码平均池层，分别生成前景和背景区域的支持度原型向量 P s = { P s , f , P s , b } ∈ R C × 1 × 1 \mathcal{P}_{s}=\{\mathcal{P}_{s,f},\mathcal{P}_{s,b}\}\in \mathbb{R}^{C\times 1 \times 1} Ps​={Ps,f​,Ps,b​}∈RC×1×1。 最后，通过计算${\mathcal{P}}_s$和${\mathcal{F}}_q$之间的余弦相似度，生成两个距离映射 D = { D f , D b } \mathcal{D}=\{\mathcal{D}_{f},\mathcal{D}_{b}\} D={Df​,Db​}，然后通过Softmax运算处理，作为最终预测${\mathcal{M}}_1=\mathrm{softmax}(\mathcal{D})$。

3.1 动机

目前的FSS方法很大程度上依赖于支持原型来分割查询对象，通过将每个查询像素与支持原型进行密集匹配。 然而，这种跨对象匹配严重地受到类内外观差异的影响，即使属于同一类，支持和查询中的对象看起来也可能非常不同。 如此高的类内变化不能仅通过少数支持来协调，因此由于查询和支持之间的外观差距很大，导致匹配结果很差。

为了验证格式塔定律在缩小这种外观差异方面的相关性，我们统计分析了Pascal VOC中跨对象和内对象像素的特征余弦相似性，其中像素特征是从ImageNet-Pretrianed Resnet-50中提取的。 表1显示，属于同一对象的像素比跨对象的像素相似得多。 值得注意的是，背景像素本身具有相似的特征，其中图像内背景像素比图像间背景像素更相似。

因此，我们建议利用查询特性来生成自我支持的原型，以匹配查询特性本身。 值得注意的是，这样的原型沿着同源的查询特征对齐查询，从而可以显著地缩小支持和查询之间的特征差距。 事后看来，自支持匹配优于传统支持查询匹配的关键原因在于，对于给定的可视对象类，对象内相似度远高于对象间相似度。

3.2 自支持原型-SSM

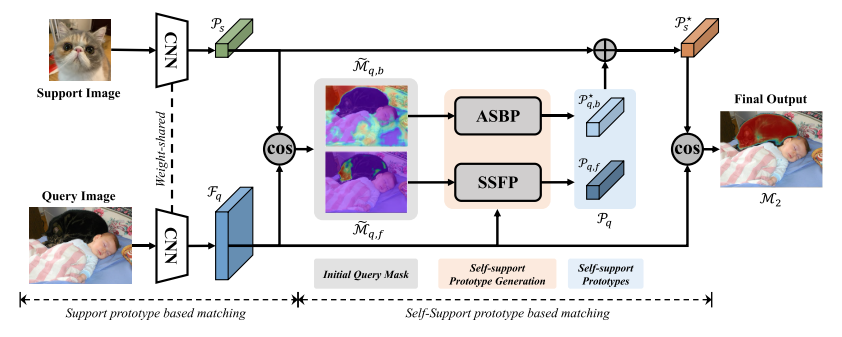
图 2. 整体自立网络架构。 我们首先使用传统的基于支持原型的匹配网络生成初始掩码预测。 然后利用初始查询掩码聚合查询特征生成自支持原型，即自支持前台原型(SSFP)和自适应自支持后台原型(ASBP)。 最后，我们结合支持原型和自支持原型来执行与查询特征的匹配。

我们的核心思想（图2）是聚合查询特性来生成查询原型，并使用它来自我支持查询特性本身。

概括地说，常规的支持原型生成过程是：
$${\mathcal{P}}_s=MAP({\mathcal{M}}_s,{\mathcal{F}}_s),$$
其中$MAP$是屏蔽平均池操作，用于生成具有查询特征${\mathcal{F}}_q$的匹配预测：
$${\mathcal{M}}_1=\mathrm{softmax}(\mathrm{cosine}({\mathcal{P}}_s,{\mathcal{F}}_q)),$$
其中余弦是余弦相似性度量。

现在，我们可以用同样的方式生成查询原型${\mathcal{P}}_q$，只是查询图像${\mathcal{M}}_q$的真值掩码在推理过程中不可用。 因此，我们需要使用预测查询掩码${\tilde{\mathcal{M}}}_q$来聚合查询特征。 查询原型生成过程可以表述为：
$${\mathcal{P}}_q=MAP({\tilde{\mathcal{M}}}_q,{\mathcal{F}}_q),$$
其中${\tilde{\mathcal{M}}}_q=1({\mathcal{M}}_1>\tau )$，${\mathcal{M}}_1$是由公式2生成的估计查询掩码，1是指示函数。

利用掩码阈值$\tau$来控制查询特征的采样范围，前台和后台的查询掩码分别设置为 { τ f g = 0.7 , τ b g = 0.6 } \{\tau_{f g}=0.7,\tau_{b g}=0.6\} {τfg​=0.7,τbg​=0.6}。 估计的自支持原型 P q = { P q , f , P q , b } {\cal P}_{q}=\{{\cal P}_{q,f},{\cal P}_{q,b}\} Pq​={Pq,f​,Pq,b​}将用于匹配查询特征。

我们理解读者对自支撑原型质量的天然关注，这是基于估计的查询掩码生成的，即估计的掩码是否能够有效地自支撑原型生成。我们发现即使是估计的查询掩码也不完美，只要它覆盖了一些有代表性的对象片段，就足以检索同一对象的其他区域。为了验证部分对象或对象片段能够支持整个对象，我们使用部分原型训练和评估模型，这些原型是根据真实掩码标签从随机选择的特征中聚合而来的。我们使用 ResNet-50 骨干在 Pascal VOC 数据集上进行了 1-shot 分割实验。如表 2 所示，在减少原型生成的聚合对象区域的同时，我们的自支撑原型始终实现高分割性能。相比之下，传统的支持原型始终获得低劣的性能，即使使用整个对象的完美支持功能。

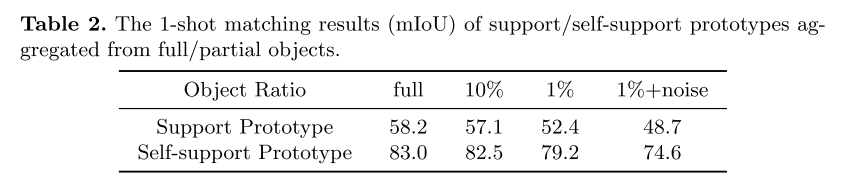
通过随机选择非目标区域的图像特征，并将这些特征聚合到上述部分原型中，在部分原型中引入20%噪声比的噪声特征，以模拟推理过程中真实的自我支持生成。 令我们惊喜的是，在这样嘈杂的环境中，我们的自助式样机仍然比传统的支持式样机工作得好得多。 注意，每个图像可能包含多个对象，因此良好的性能表明我们的自支持原型也可以很好地处理多对象场景。 这些结果证实了我们的自支撑样机在实际应用中的实用性和优越性。

3.3 自适应自支持背景原型-ASBP

前景像素具有语义共性，这构成了我们在查询特征和前景对象支持原型之间自动支持原型生成和匹配过程的基本原理。 因此，我们可以利用屏蔽平均池来生成自我支持的前景原型（图3(a)):

$${\mathcal{P}}_{q,f}=MAP({\tilde{\mathcal{M}}}_{q,f},{\mathcal{F}}_q),$$
其中${\tilde{\mathcal{M}}}_{q,f}$是前面提到的估计查询掩码。

另一方面，背景可能是杂乱的，在不相交的区域中，共性可以被简化为局部语义相似性，而不是所有背景像素之间共享的全局语义共性。 例如，对于一个以狗为目标类的查询图像，人和车等其他对象都被视为背景，但它们在外观和语义层次上都是不同的。 如表1所示，与前景像素相比，背景像素相似性更小，这也验证了这一观察，尤其是在对象/图像内的情况下。 这促使我们为不同的查询语义区域生成多个自支持背景原型。

一个简单的解决方案是使用聚类算法直接对多个背景原型进行分组，然后在每个查询像素处选择最相似的原型进行背景匹配。 这种显式背景分组在很大程度上依赖于聚类算法，该算法不稳定且耗时。 因此，我们提出了一种更加灵活高效的方法，为每个查询像素自适应地生成自我支持的背景原型（图3(b))。

其思想是为每个查询像素动态聚合相似的背景像素，以生成自适应的自我支持背景原型。

具体来说，我们首先通过对查询特征${\mathcal{F}}_q$与背景掩码${\tilde{\mathcal{M}}}_{q,b}$进行掩码乘法来收集背景查询特征${\mathcal{F}}_{q,b}\in {\mathbb{R}}^{C\times M}$，其中$M$是背景区域的像素个数。 然后我们可以通过矩阵乘法运算$Matmul$生成重塑后的背景查询特征${\mathcal{F}}_{q,b}$和全查询特征${\mathcal{F}}_q$的像素之间的亲和力矩阵$\mathcal{A}$：
$$\mathcal{A}=MatMul({{\mathcal{F}}_{q,b}}^T,{\mathcal{F}}_q),$$
其中$\mathcal{A}$的大小为${\mathbb{R}}^{M\times (H\times W)}$。 在第一维上通过Softmax运算对亲和力矩阵进行归一化，并对每个查询像素的背景查询特征进行加权聚合，生成自适应自支持背景原型${\mathcal{P}}_{q,b}^{\star }\in {\mathbb{R}}^{C\times H\times W}$：
$${\mathcal{P}}_{q,b}^{\star }=Mat\mathrm{Mul}({\mathcal{F}}_{q,b},\mathrm{softmax}(\mathcal{A})).$$
用自适应的自支持背景原型更新自支持原型: P q = { P q , f , P q , b ⋆ } . \mathcal{P}_{q}=\{\mathcal{P}_{q,f},\mathcal{P}_{q,b}^{\star}\}. Pq​={Pq,f​,Pq,b⋆​}.。

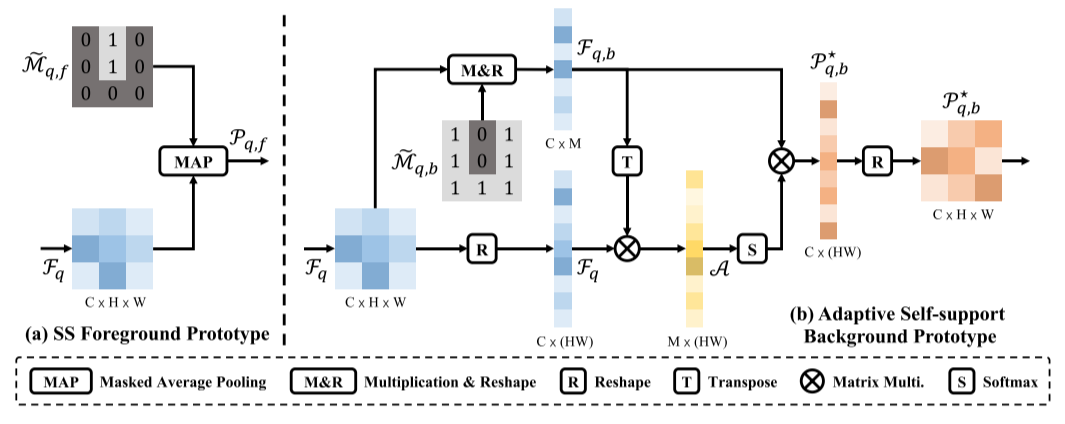
原型生成

(a)自我支持(SS)前景原型

(b)自适应自我支持背景原型。

3.4 自支持匹配-SSL

我们加权组合了支持原型${\mathcal{P}}_s$和自我支持原型${\mathcal{P}}_q$：

$${\mathcal{P}}_s^{\star }={\alpha }_1{\mathcal{P}}_s+{\alpha }_2{\mathcal{P}}_q,$$
其中，${\alpha }_1$和${\alpha }_2$是调谐权重，我们在实验中设置${\alpha }_1={\alpha }_2=0.5$。 然后我们计算增强支持度原型${\mathcal{P}}_s^{\star }$和查询特征${\mathcal{F}}_q$之间的余弦距离来生成最终的匹配预测：
$${\mathcal{M}}_2=\mathrm{softmax}(\mathrm{cosine}({\mathcal{P}}_s^{\star },{\mathcal{F}}_q)).$$
然后我们在生成的距离进行有监督训练监督：
$${\mathcal{L}}_m=BCE(\mathrm{cosine}({\mathcal{P}}_s^{\star },{\mathcal{F}}_q),{\mathcal{G}}_q),$$
其中$BCE$是二值交叉熵损失，${\mathcal{G}}_q$是查询图像的真值掩码。

为了进一步简化自支持匹配过程，我们提出了一种新的查询自支持丢失。 对于查询特性${\mathcal{F}}_q$及其原型${\mathcal{P}}_q$，我们应用以下训练监督：
$${\mathcal{L}}_q=BCE(\mathrm{cosine}({\mathcal{P}}_q,{\mathcal{F}}_q),{\mathcal{G}}_q).$$
我们可以在支持度特征上应用同样的过程来引入支持度自匹配损失${\mathcal{L}}_s$。

最后，我们通过联合优化前述所有损失，以端到端的方式训练模型：
$$\mathcal{L}={\lambda }_1{\mathcal{L}}_m+{\lambda }_2{\mathcal{L}}_q+{\lambda }_3{\mathcal{L}}_s,$$
其中λ1=1.0，λ2=1.0，λ3=0.2是损失权重。

3. 代码

原生代码写的非常的不错。我这里做了注释。

from .resnet import resnet50, resnet101

import torch
from torch import nn
import torch.nn.functional as F


class SSP_MatchingNet(nn.Module):
    def __init__(self, backbone, pretrained=True, refine=False):
        super(SSP_MatchingNet, self).__init__()
        backbone = eval(backbone)(pretrained=pretrained)  # 创建backbone
        self.layer0 = nn.Sequential(backbone.conv1, backbone.bn1, backbone.relu, backbone.maxpool)
        self.layer1, self.layer2, self.layer3 = backbone.layer1, backbone.layer2, backbone.layer3
        self.refine = refine

    def forward(self, img_s_list, mask_s_list, img_q, mask_q):
        """

        Args:
            img_s_list: support images
                        List   shape=shot x [batch size,3,473,473]
            mask_s_list: masks for support images 
                    List  shape=shot x [batch size,473,473]
            img_q:  query images
                    [batch_size,3,473,473]
            mask_q:  query images
                    [batch_size,473,473]
        """
        h, w = img_q.shape[-2:]

        # feature maps of support images
        feature_s_list = []
        #  获取支持集的特征
        for k in range(len(img_s_list)):
            with torch.no_grad():
                s_0 = self.layer0(img_s_list[k])
                s_0 = self.layer1(s_0)  # [4,256,119,119]
            s_0 = self.layer2(s_0)  # [4,256,119,119]-> [4,256,60,60]
            s_0 = self.layer3(s_0)  # [4,256,60,60] -> [4,1024,60,60]
            feature_s_list.append(s_0)
            del s_0

        # 获取查询集图像的特征
        with torch.no_grad():
            q_0 = self.layer0(img_q)
            q_0 = self.layer1(q_0)
        q_0 = self.layer2(q_0)
        feature_q = self.layer3(q_0)  # [4,1024,60,60]

        # foreground(target class) and background prototypes pooled from K support features
        feature_fg_list = []
        feature_bg_list = []
        supp_out_ls = []
        for k in range(len(img_s_list)):
            # feature_fg=[1,4,1024]
            feature_fg = self.masked_average_pooling(feature_s_list[k], (mask_s_list[k] == 1).float())[None, :]
            # feature_bg=[1,4,1024]
            feature_bg = self.masked_average_pooling(feature_s_list[k], (mask_s_list[k] == 0).float())[None, :]
            feature_fg_list.append(feature_fg)
            feature_bg_list.append(feature_bg)

            if self.training:

                # 自支持损失 SSL
                # [4,60,60] 。支持集图像的原型 来分割 支持集图像
                supp_similarity_fg = F.cosine_similarity(feature_s_list[k], feature_fg.squeeze(0)[..., None, None], dim=1)
                # [4,60,60]
                supp_similarity_bg = F.cosine_similarity(feature_s_list[k], feature_bg.squeeze(0)[..., None, None], dim=1)
                # [4,2,60,60]
                supp_out = torch.cat((supp_similarity_bg[:, None, ...], supp_similarity_fg[:, None, ...]), dim=1) * 10.0
                supp_out = F.interpolate(supp_out, size=(h, w), mode="bilinear", align_corners=True)  # [4,2,473,473]
                supp_out_ls.append(supp_out)

        # 对shot个图片进行平均，计算原型 [4,1024,1,1]
        FP = torch.mean(torch.cat(feature_fg_list, dim=0), dim=0).unsqueeze(-1).unsqueeze(-1)
        # 背景原型 [4,1024,1,1]
        BP = torch.mean(torch.cat(feature_bg_list, dim=0), dim=0).unsqueeze(-1).unsqueeze(-1)

        # 计算查询特征和前景和背景的原型 之间的相似度。计算出初步的分割掩码
        out_0 = self.similarity_func(feature_q, FP, BP)  # [4,2,60,60]

        ##################### Self-Support Prototype (SSP) #####################
        # SSFP_1=[4,1024,1,1],SSBP_1=[4,1024,1,1],ASBP_1=[4,1024,60,60] ,ASFP_1=[4,1024,60,60]
        SSFP_1, SSBP_1, ASFP_1, ASBP_1 = self.SSP_func(feature_q, out_0)  
        
        FP_1 = FP * 0.5 + SSFP_1 * 0.5  # [4,1024,1,1]
        BP_1 = SSBP_1 * 0.3 + ASBP_1 * 0.7  # [4,1024,1,1]

        out_1 = self.similarity_func(feature_q, FP_1, BP_1)  # [4,2,60,60]

        ##################### SSP Refinement #####################
        if self.refine:
            SSFP_2, SSBP_2, ASFP_2, ASBP_2 = self.SSP_func(feature_q, out_1)

            FP_2 = FP * 0.5 + SSFP_2 * 0.5
            BP_2 = SSBP_2 * 0.3 + ASBP_2 * 0.7

            FP_2 = FP * 0.5 + FP_1 * 0.2 + FP_2 * 0.3
            BP_2 = BP * 0.5 + BP_1 * 0.2 + BP_2 * 0.3

            out_2 = self.similarity_func(feature_q, FP_2, BP_2)

            out_2 = out_2 * 0.7 + out_1 * 0.3

        # out_0 = F.interpolate(out_0, size=(h, w), mode="bilinear", align_corners=True)
        out_1 = F.interpolate(out_1, size=(h, w), mode="bilinear", align_corners=True)  # [4,2,473,473]

        if self.refine:
            out_2 = F.interpolate(out_2, size=(h, w), mode="bilinear", align_corners=True)
            out_ls = [out_2, out_1]
        else:
            out_ls = [out_1]

        if self.training:

            # 自支持损失 SSL
            fg_q = self.masked_average_pooling(feature_q, (mask_q == 1).float())[None, :].squeeze(0)  # [4,1024]
            bg_q = self.masked_average_pooling(feature_q, (mask_q == 0).float())[None, :].squeeze(0)  # [4,1024]

            self_similarity_fg = F.cosine_similarity(feature_q, fg_q[..., None, None], dim=1)  # [4,60,60]
            self_similarity_bg = F.cosine_similarity(feature_q, bg_q[..., None, None], dim=1)  # [4,60,60]
            self_out = torch.cat((self_similarity_bg[:, None, ...], self_similarity_fg[:, None, ...]), dim=1) * 10.0  # [4,2,60,60]

            self_out = F.interpolate(self_out, size=(h, w), mode="bilinear", align_corners=True)
            supp_out = torch.cat(supp_out_ls, 0)

            out_ls.append(self_out)
            out_ls.append(supp_out)

        return out_ls

    def SSP_func(self, feature_q, out):
        """
        查询编码 和 分割结果
        """
        bs = feature_q.shape[0]  # [4,1024,60,60] 查询编码
        pred_1 = out.softmax(1)  # [4,2,60,60]-> [4,2,60,60] 分割结果
        pred_1 = pred_1.view(bs, 2, -1)  # [4,2,3600]
        pred_fg = pred_1[:, 1]  # [4,3600] # 前景分割概率
        pred_bg = pred_1[:, 0]  # [4,3600] # 背景分割概率
        fg_ls = []
        bg_ls = []
        fg_local_ls = []
        bg_local_ls = []
        for epi in range(bs):
            fg_thres = 0.7  # 0.9 #0.6
            bg_thres = 0.6  # 0.6
            cur_feat = feature_q[epi].view(1024, -1)  # [1024,3600] 当前query特征
            f_h, f_w = feature_q[epi].shape[-2:]

            # step 1: 通过对查询特征 与 背景掩码 进行掩码乘法来收集背景查询特征
            if (pred_fg[epi] > fg_thres).sum() > 0:
                fg_feat = cur_feat[:, (pred_fg[epi] > fg_thres)]  # .mean(-1) #选出前景特征
            else:
                fg_feat = cur_feat[:, torch.topk(pred_fg[epi], 12).indices]  # .mean(-1)
            if (pred_bg[epi] > bg_thres).sum() > 0:
                bg_feat = cur_feat[:, (pred_bg[epi] > bg_thres)]  # .mean(-1)
            else:
                bg_feat = cur_feat[:, torch.topk(pred_bg[epi], 12).indices]  # .mean(-1) # 选出背景特征

            # global proto
            fg_proto = fg_feat.mean(-1)  # 高置信度的前景的原型
            bg_proto = bg_feat.mean(-1)  # 高置信度的背景的原型
            fg_ls.append(fg_proto.unsqueeze(0))
            bg_ls.append(bg_proto.unsqueeze(0))

            # local proto
            fg_feat_norm = fg_feat / torch.norm(fg_feat, 2, 0, True)  # 1024, N1 高置信度的前景的特征
            bg_feat_norm = bg_feat / torch.norm(bg_feat, 2, 0, True)  # 1024, N2 高置信度的背景的特征
            cur_feat_norm = cur_feat / torch.norm(cur_feat, 2, 0, True)  # 1024, N3

            cur_feat_norm_t = cur_feat_norm.t()  # N3, 1024

            # step 2: 通过矩阵乘法运算生成亲和力矩阵A
            fg_sim = torch.matmul(cur_feat_norm_t, fg_feat_norm) * 2.0  # N3, N1
            bg_sim = torch.matmul(cur_feat_norm_t, bg_feat_norm) * 2.0  # N3, N2

            # 第一维上通过Softmax运算对亲和力矩阵进行归一化
            fg_sim = fg_sim.softmax(-1)
            bg_sim = bg_sim.softmax(-1)

            # 生产自适应背景原型
            fg_proto_local = torch.matmul(fg_sim, fg_feat.t())  # N3, 1024
            bg_proto_local = torch.matmul(bg_sim, bg_feat.t())  # N3, 1024

            fg_proto_local = fg_proto_local.t().view(1024, f_h, f_w).unsqueeze(0)  # 1024, N3
            bg_proto_local = bg_proto_local.t().view(1024, f_h, f_w).unsqueeze(0)  # 1024, N3

            
            fg_local_ls.append(fg_proto_local)
            bg_local_ls.append(bg_proto_local)

        # global proto
        new_fg = torch.cat(fg_ls, 0).unsqueeze(-1).unsqueeze(-1)
        new_bg = torch.cat(bg_ls, 0).unsqueeze(-1).unsqueeze(-1)

        # local proto
        new_fg_local = torch.cat(fg_local_ls, 0).unsqueeze(-1).unsqueeze(-1)
        new_bg_local = torch.cat(bg_local_ls, 0)

        return new_fg, new_bg, new_fg_local, new_bg_local

    def similarity_func(self, feature_q, fg_proto, bg_proto):
        """
         通过计算相似度来进行分割
         feature_q: [4,1024,60,60] 查询集特征
         fg_proto: [4,1024,1,1] 前景原型
         bg_proto: [4,1024,1,1] 背景原型
         结果: [4,2,60,60] 初步的分割结果
        """

        similarity_fg = F.cosine_similarity(feature_q, fg_proto, dim=1)
        similarity_bg = F.cosine_similarity(feature_q, bg_proto, dim=1)

        out = torch.cat((similarity_bg[:, None, ...], similarity_fg[:, None, ...]), dim=1) * 10.0  # [4,2,60,60]
        return out

    def masked_average_pooling(self, feature, mask):
        """
        通过mask_pool操作获取对应特征的原型。
        feature: [4,1024,60,60]
        mask:  [4,473,473]
        return feature : [4,1024]
        """
        # [4,473,473] -> [4,1,60,60]
        mask = F.interpolate(mask.unsqueeze(1), size=feature.shape[-2:], mode='bilinear', align_corners=True)
        masked_feature = torch.sum(feature * mask, dim=(2, 3)) / (mask.sum(dim=(2, 3)) + 1e-5)
        return masked_feature

ECCV 2022 | SSP: 自支持匹配的小样本任务新思想 - 知乎 (zhihu.com)

(4条消息) 【小样本分割】Self-Support Few-Shot Semantic Segmentation_小样本语义分割_栗子菜菜的博客-CSDN博客