题目链接：HDU-5961 传递
中文题面就不解释题目意思，解释一下名词的意思
完全图：对于一个无向图 $G$ 而言，设点集为 $V$，点集中任意不相同两点 $u,v$ 间都有且仅有一条边叫做完全图。
竞赛图：在一个完全图的基础上给所有边定向，就变成了竞赛图。
可传递：在一个有向图中若存在边 $(a\to b)$（代表一条由 $a$ 指向 $b$ 的边，下同），和 $(b\to c)$。则一定要存在边 $(a\to c)$ 若不存在即不合法。

拓扑排序

思路

我认为的正解，很妙的反向建图的思路，一直思考暴力没往这方面想。

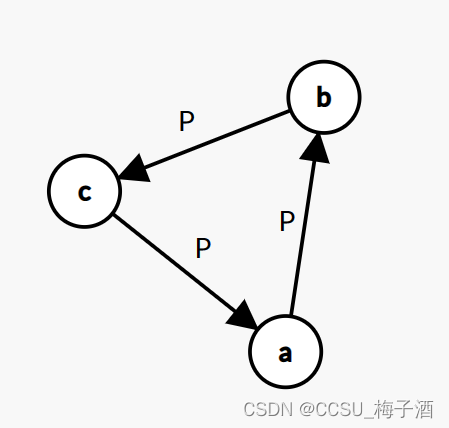
考虑任意图不合法的情况

1. 有环存在同一图中：$(a\to b)(b\to c)(c\to a)$。
   

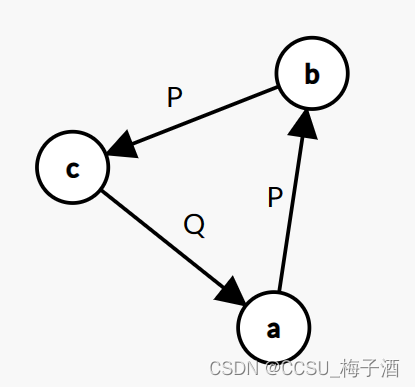
2. 存在需要满足可传递的前置情况，却少了边
   $P$ 图：$(a\to b)(b\to c)$ (理应要有 $(a\to c)$ 才合法，但这条边却存在与另一图中)
   $Q$ 图：$(a\to c)/(c\to a)$
   
   

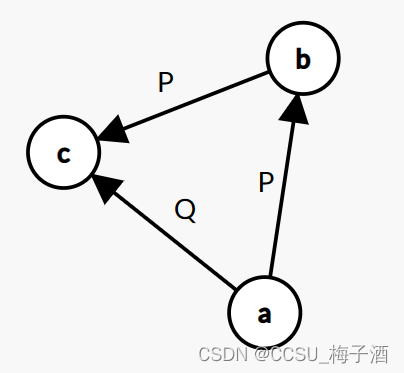
情况1：只需要对图跑一遍拓扑排序判环即可解决。
情况2：因为竞赛图是在完全图基础上定向而来，那么如果一个图P仅有 $(a\to b)(b\to c)$，没有 $(a\to c)/(c\to a)$。
不是情况1的环但也不合法， 但 $(a\to c)/(c\to a)$ 一定会存在另一张图 $Q$ 中。
如果 $Q$ 图中存在的是 $(c\to a)$，那么我们如果将两个图合并起来，就会形成 $(a\to b)(b\to c)(c\to a)$ 的环。
如果存在的是 $(a\to c)$，那么我们将 $Q$ 图的边反向再与图 $P$ 合并那么也将构成环。

于是得出结论：将 $P，Q$ 图中任意一个反向记为 $Q^{\prime }$(不妨假设将 $Q$ 反向)
将图 $P,Q$ 合并拓扑排序判环，再将图 $P,Q^{\prime }$ 合并拓扑排序判环 任意情况有环即不合法。

网上很多题解都仅仅是将图 $Q$ 反向与 $P$ 合并判环，而没有将原图$Q$ 与 $P$ 反向判环这是错误的，两者都需要才能正确判断，这里提供一个hack样例。

input:
2
3
-P-
--P
Q--
3
-PQ
--P
---

output:
N
N

代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 2023;
char mp[N][N];

int n, head[N], in[N], tot;
struct edge{
    int to, nex;
}e[N * N];

void add(int from, int to){
    in[to] ++;
    e[++ tot].to = to;
    e[tot].nex = head[from];
    head[from] = tot;
}

void build(int op){ // 建图
    tot = 0;
    for(int i = 1; i <= n; i ++) {
        in[i] = head[i] = 0;
    }
    for(int i = 1; i <= n; i ++){
        for(int j = 1; j <= n; j ++){
            if(mp[i][j] == 'P') add(i, j);
            if(mp[i][j] == 'Q'){ 
                if(op == 1) add(i, j); // 正
                else add(j, i); // 反
            }
        }
    }
}

queue<int>q;
bool topsort(int op){
    build(op);
    vector<int>cnt;
    
    for(int i = 1; i <= n; i ++){
        if(!in[i]) q.push(i);
    }

    while(!q.empty()){
        int u = q.front(); q.pop();
        cnt.push_back(u);
        for(int i = head[u]; i; i = e[i].nex){
            int v = e[i].to; in[v] --;
            if(!in[v]) q.push(v);
        }
    }
    return (int)cnt.size() == n;
}

void solve(){
    scanf("%d",&n);
    for(int i = 1; i <= n; i ++){
        scanf("%s", mp[i] + 1);
    }
    
    if(!topsort(1) || !topsort(0)) puts("N");
    else puts("T");
}

int main(){
    int t;
    scanf("%d",&t);
    while(t --){
        solve();
    }
    return 0;
}

暴力

思路

将图用邻接表存（vector / 链式前向星）对两个图分别三重for循环暴力判断。注意这种方法是可以被hack掉的，但是不知道是赛时数据弱还是怎么回事，能成功AC。
接下来给出hack样例和构造方法：其实就是让所有边都只存在一张图 $P$ 中并且该图合法，任意点都指向编号大于自己的其他点，然后将数据拉满 $T=8,n=2000$ 即可。
hack样例

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 2023;
char mp[N][N];

int vis[N], n;
bool flag;
vector<int>g[2][N];

bool check(int op){
    for(int i = 1; i <= n; i ++){
        for(int j = 0; j < g[op][i].size(); j ++){
            int u = g[op][i][j];
            for(int k = 0; k < g[op][u].size(); k ++){
                int v = g[op][u][k];
                if(op == 0 && mp[i][v] != 'Q') return true;
                if(op == 1 && mp[i][v] != 'P') return true;
            }
        }
    }
    return false;
}
void solve(){
    scanf("%d",&n);
    for(int i = 1; i <= n; i ++){
        scanf("%s", mp[i] + 1);
        g[0][i].clear();
        g[1][i].clear();
    }

    for(int i = 1; i <= n; i ++){
        for(int j = 1; j <= n; j ++){
            if(mp[i][j] == '-') continue ;
            g[mp[i][j] == 'P'][i].push_back(j);
        }
    }
    if(check(1) || check(0)) puts("N");
    else puts("T");
}

int main(){
    int t;
    scanf("%d",&t);
    while(t --){
        solve();
    }
    return 0;
}

bitset优化暴力

可以看这位老哥的 WA是一笔财富