BSTree
- 0 引言
- 1 二叉搜索树的概念
- 2 创建一棵二叉搜索树(插入操作)
- 2.1 画图分析插入操作
- 2.2 代码思路
- 2.3 利用中序遍历验证
- 3 二叉搜索树的查找操作
- 4 二叉树搜索树的删除操作(重点)
- 4.1 代码的一些细节分析
- 5 总结
0 引言
本篇文章会在VS2019下以代码+图片的方式一步一步分析二叉搜索树的插入、删除、查找操作。文章的重点会放在删除操作上。
1 二叉搜索树的概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
如图所示是一棵二叉搜索树:
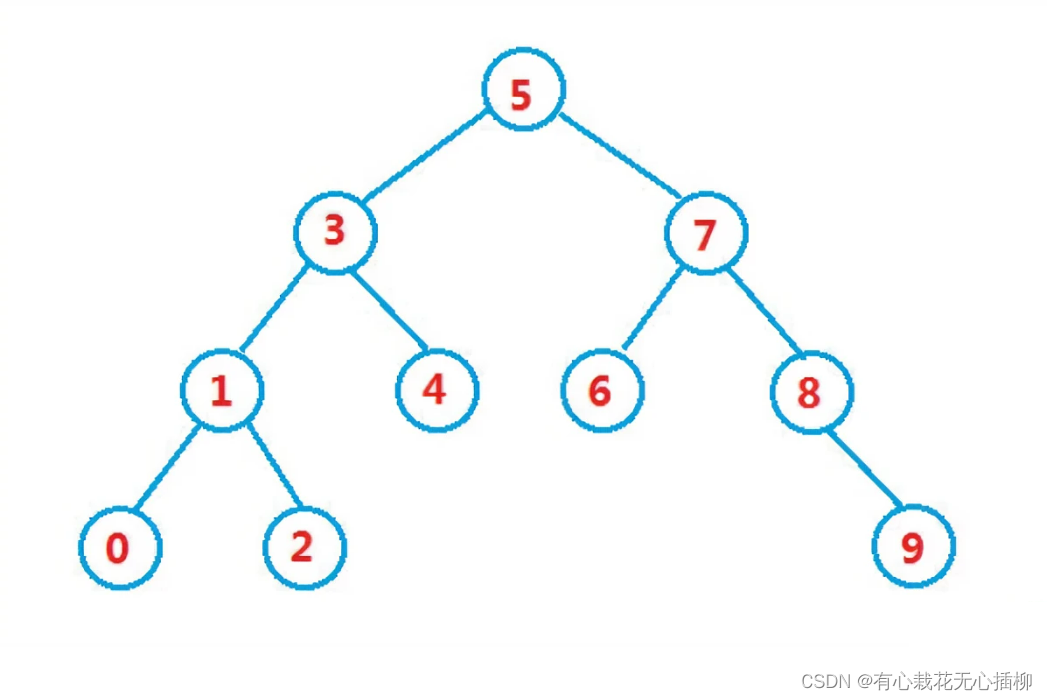
值得一提的是,因为二叉搜索树独特的性质,我们对它进行中序遍历后,就会发现得到的结果是已经排序好的。所以也叫二叉排序树
如上图,中序遍历后的结果是:
0 1 2 3 4 5 6 7 8 9
2 创建一棵二叉搜索树(插入操作)
首先,我们要定义出树的结点的结构体
template <class K>
struct BSTreeNode //定义结点的结构体
{
BSTreeNode<K>* left;
BSTreeNode<K>* right;
K _key;
BSTreeNode(const K& key)//初始化
:left(nullptr), right(nullptr), _key(key)
{}
};
然后开始设计二叉搜索树的结构
template <class K>
class BSTree
{
typedef BSTreeNode<K> Node;//节点名称
public:
//插入,删除,查找操作函数写在这
private:
Node* root = nullptr;//初始化根结点为空
};
接下来就是利用插入操作来创建出一棵二叉搜索树
我们初始数据就以这幅图为例
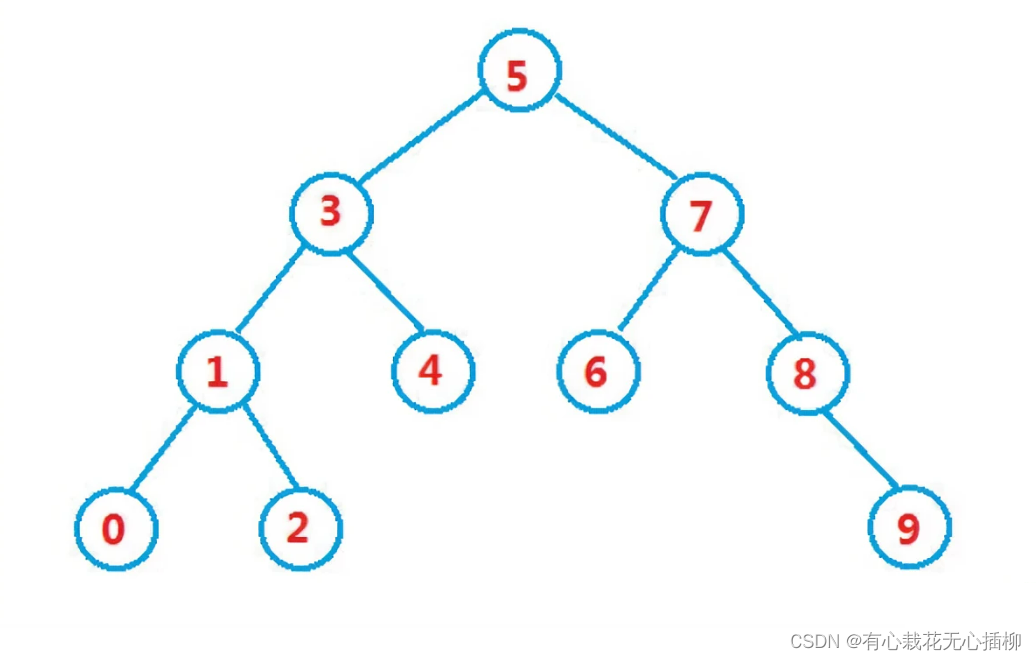
int a[] = { 5,3,7,1,4,6,8,0,2,9 };
2.1 画图分析插入操作
插入的规则就是,要插入的结点从根结点开始比较,比当前结点大就往右继续比较,比当前结点小就往左比较,直到比较到空为止。如果当前结点等于我要插入的值,就不能再继续比较了,因为二叉搜索树不允许有重复的元素。
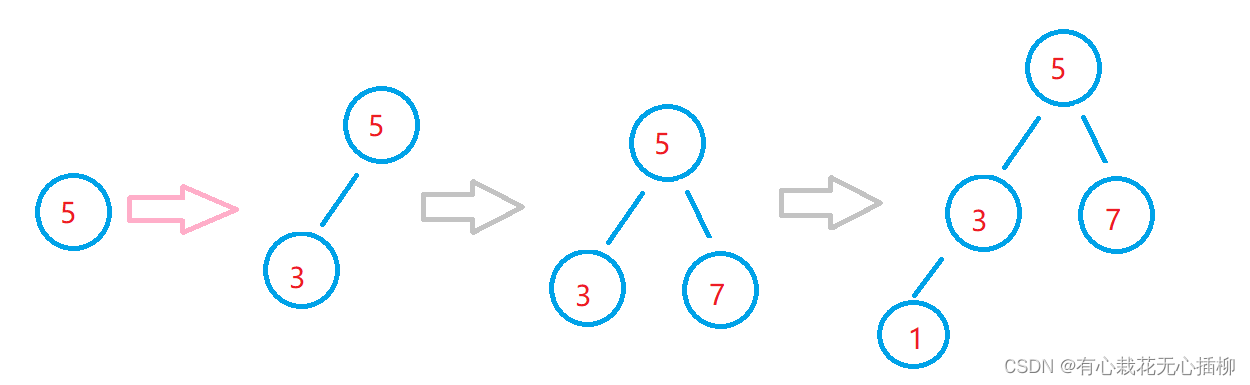
首先,插入的时候,原先数组的数据的顺序是会影响到二叉搜索树的结构的。因为我们是按照数组的从左往右遍历插入的。
这里一开始root为空,会先创建一个5结点。
然后按照数组顺序,创建一个3结点,由于3比5小,所以3结点会在5结点的左子树
然后继续准备插入7结点,由于7比5大,所以7结点会在5结点的右子树。
以此类推,完整的二叉搜索树如下
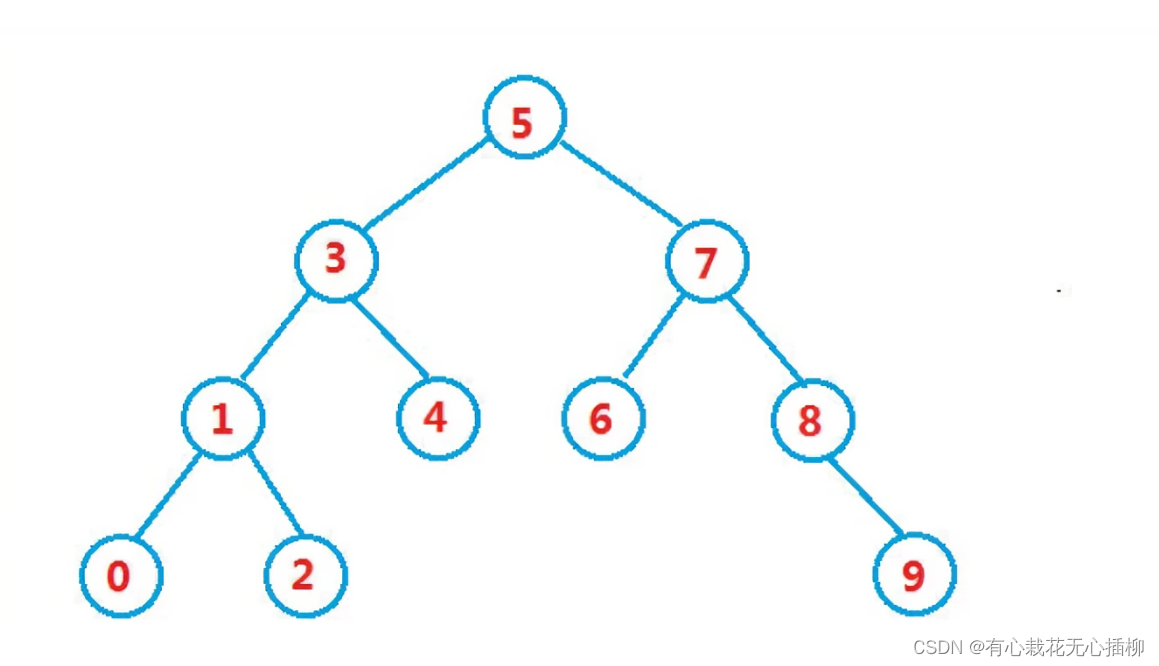
2.2 代码思路
插入操作的代码思路很简单,几个判断语句就搞定了。
需要注意的是,我们比较到空的时候,需要记录上一个结点才能插入,否则无法和上一个结点链接上。
bool insert(const K& key)//插入成功返回true,插入失败返回false,遇到重复元素就会返回false
{
if (root == nullptr)//如果一开始为空,该树就没有结点,创建一个新结点就即可
{
root = new Node(key);
return true;
}
else//一开始不为空,需要插入的元素从根结点开始比较了
{
Node* parent = nullptr;//在往下比较的过程中记录上一个结点,方便最后的插入链接
Node* cur = root;//当前需要比较的结点
while (cur)//不为空就继续比较
{
if (cur->_key < key)//如果要插入的元素大于当前的结点元素
{
parent = cur;
cur = cur->right;//往右子树走
}
else if (cur->_key > key)//否则往左走
{
parent = cur;
cur = cur->left;
}
else//如果相等的话就返回false,因为不允许有重复元素
{
return false;
}
}
//代码走到这里说明cur为空了,我们利用这个cur创建一个结点
cur = new Node(key);
//比较要插入的元素和上一个结点的大小
//比上一个结点大就插入右边
if (key > parent->_key)
{
parent->right = cur;
}
else//否则插入左边
{
parent->left = cur;
}
}
return true;//代码走到这里说明插入成功
}
2.3 利用中序遍历验证
这是写在类里面的中序遍历代码
这里有个小技巧,我们嵌套了函数,方便调用的时候可以不用传参
void _InOrder(Node* root)//中序遍历
{
if (root == nullptr) return;
_InOrder(root->left);
cout << root->_key << " ";
_InOrder(root->right);
}
void InOrder()//要调用的函数
{
_InOrder(root);
}
代码执行结果如下:
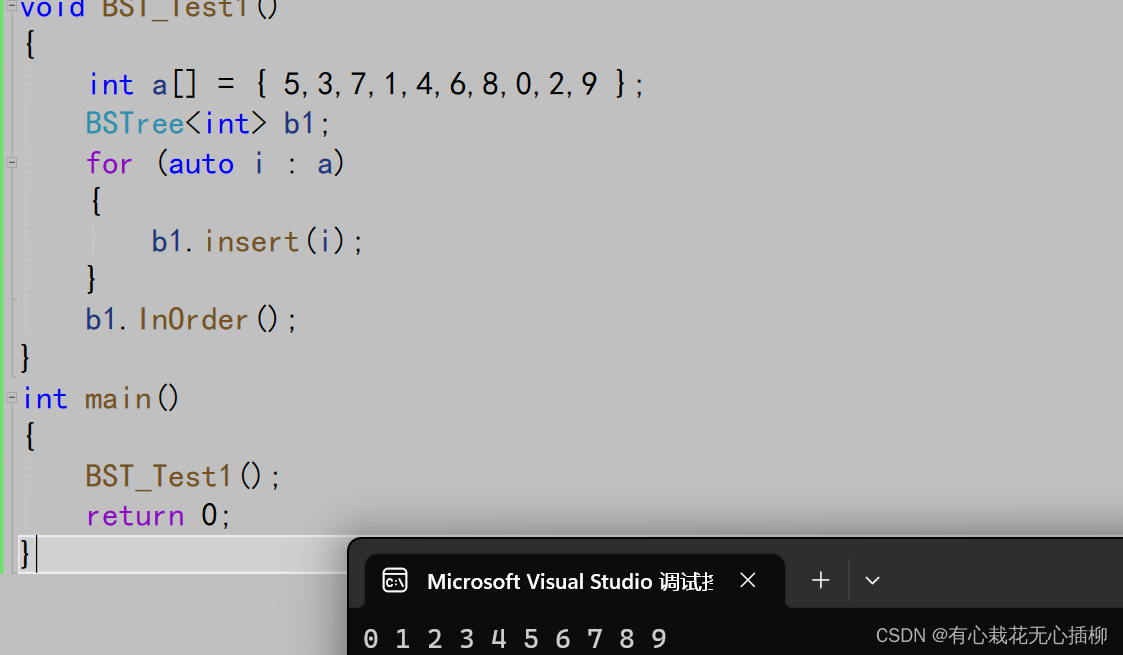
3 二叉搜索树的查找操作
查找操作和刚才的插入操作思路差不多,都是从根结点开始比较,不过查找操作是找到该元素为止或者走到空为止。
比如,我们现在要插入2这个元素,2比5小往左子树走,2比3小,往左子树走,2比1大,往右子树走,这时候找到了2这个元素,停止比较。
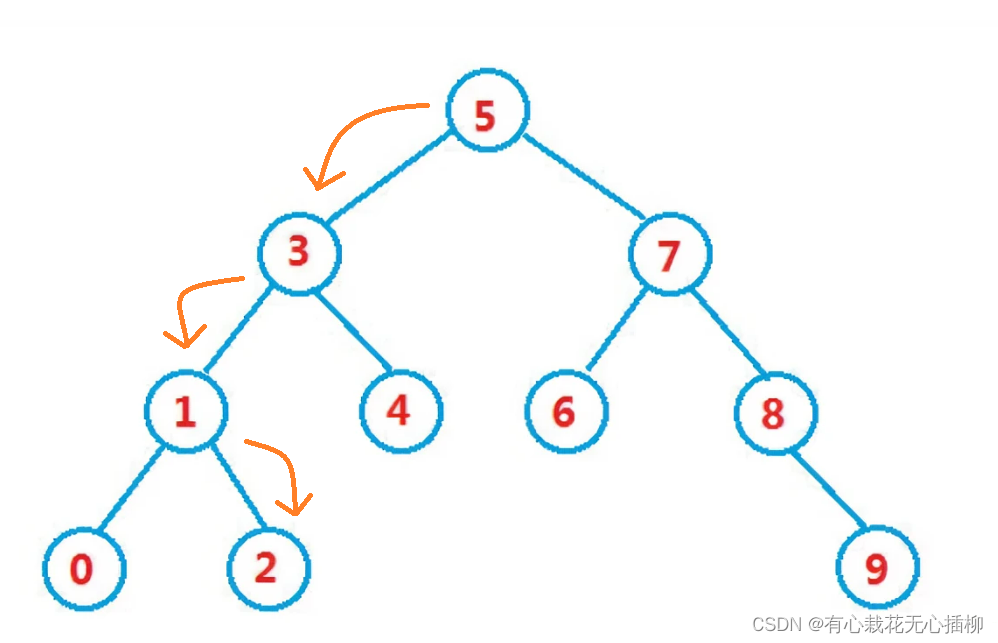
直接上代码:
bool find(const K& key)
{
if (root == nullptr) return false;//如果根结点为空,就返回false,表示未找到
Node* cur = root;
while (cur)//从根结点比较
{
if (cur->_key < key)//要查找的元素比当前元素大,就往右子树走
{
cur = cur->right;
}
else if (cur->_key > key)//否则就往左子树走
{
cur = cur->left;
}
else//相等,返回true,说明找到了
{
return true;
}
}
return false;//走到这里说明cur为空了还未找到,二叉搜索树里没有该结点,直接返回false
}
测试代码如下:
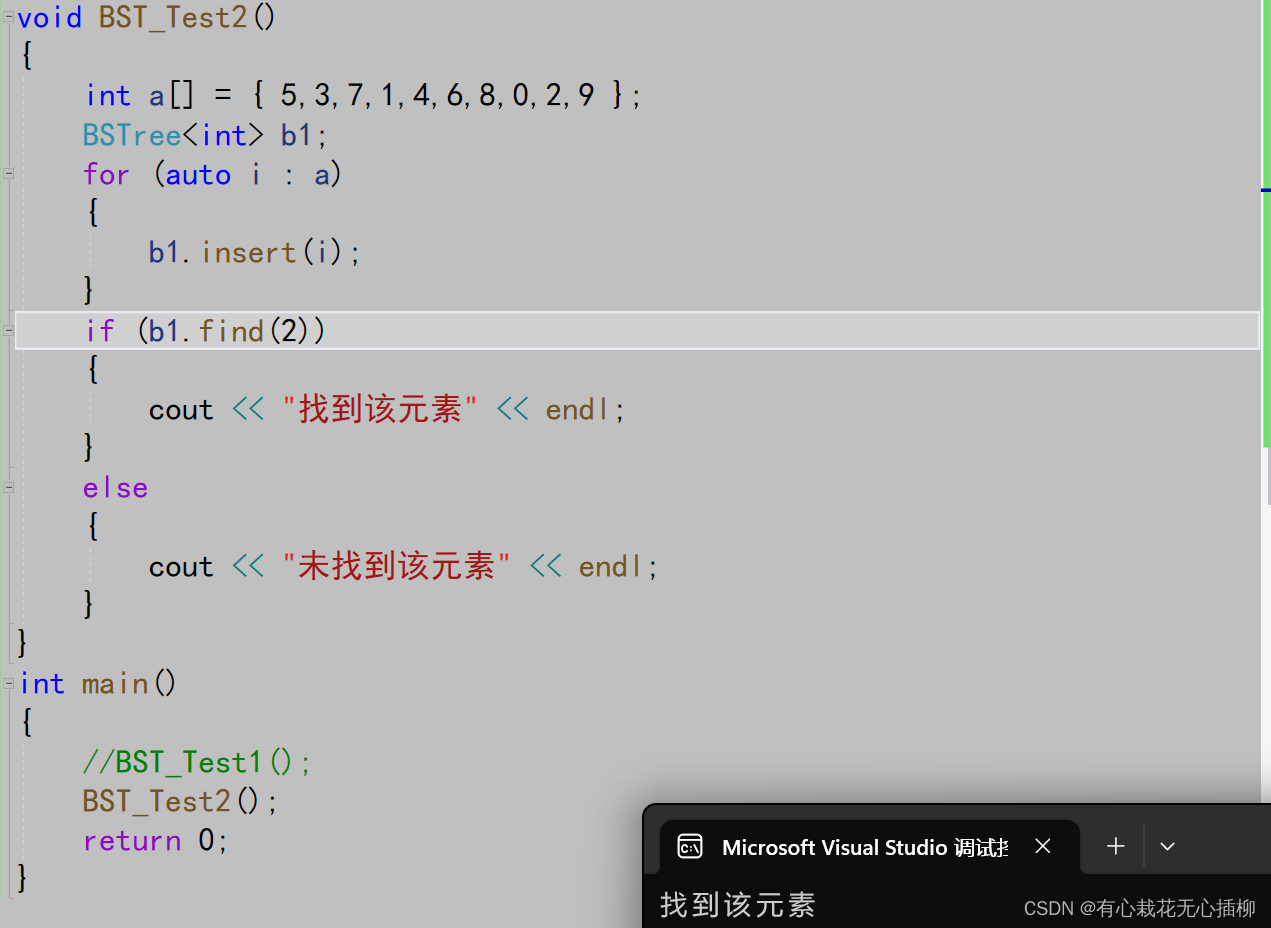
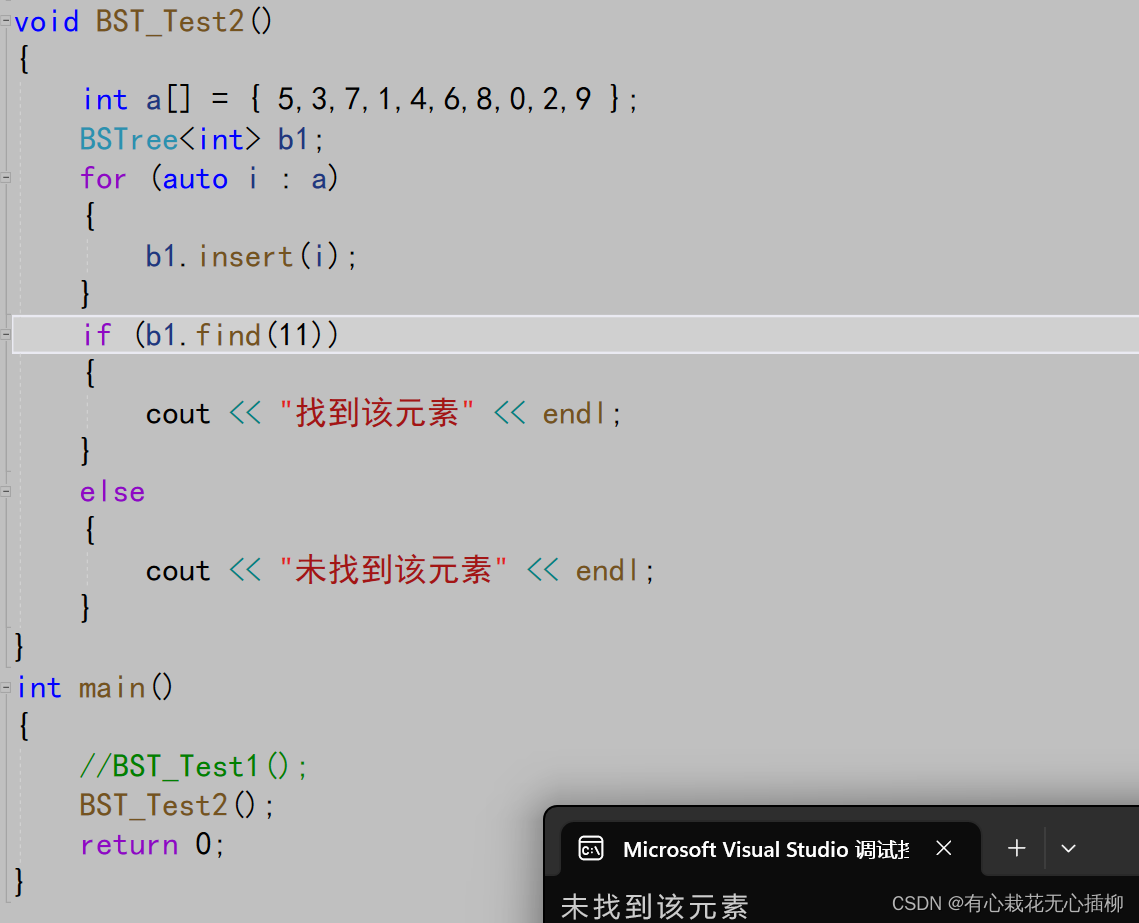
4 二叉树搜索树的删除操作(重点)
二叉搜索树的重头戏是删除操作,因为删除了一个结点,可能会影响到多个结点,也可能不会影响。接下来,我们分类讨论。
1.被删除的结点是叶节点
这种情况比较简单,因为在叶节点上,删除后不会影响到其他结点,我们直接删除即可。
如图,我们要删除9这个叶结点,直接删除即可。
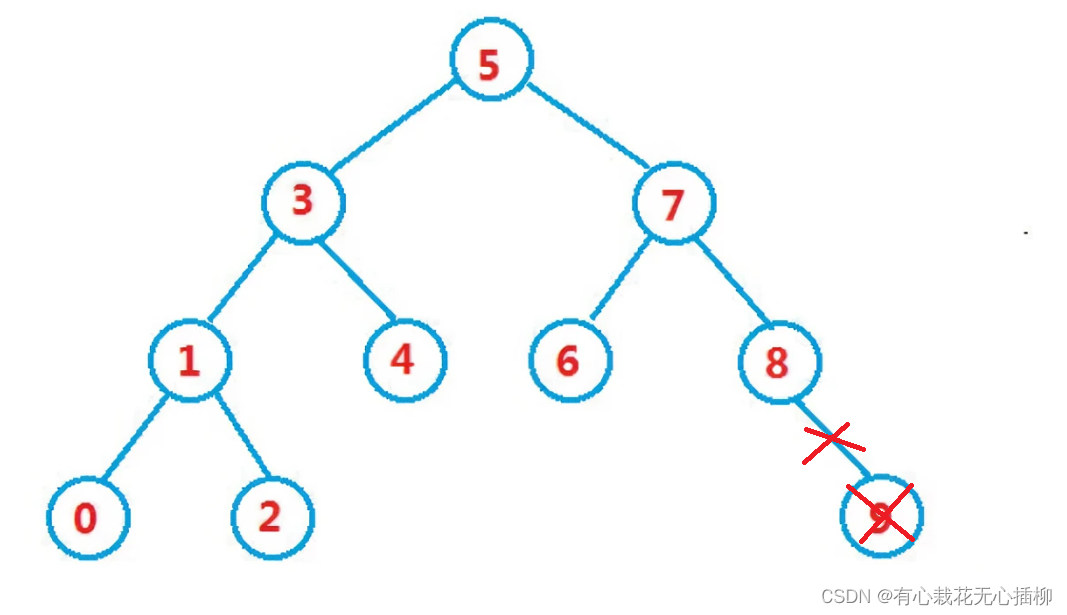
2.被删除的结点只有一个孩子
如果被删除的结点只有一个孩子,我们直接让被删除的结点的父结点领养这个孩子即可。
之所以能被领养,是因为一个结点能管理两个孩子,所以这种思路是可行的。
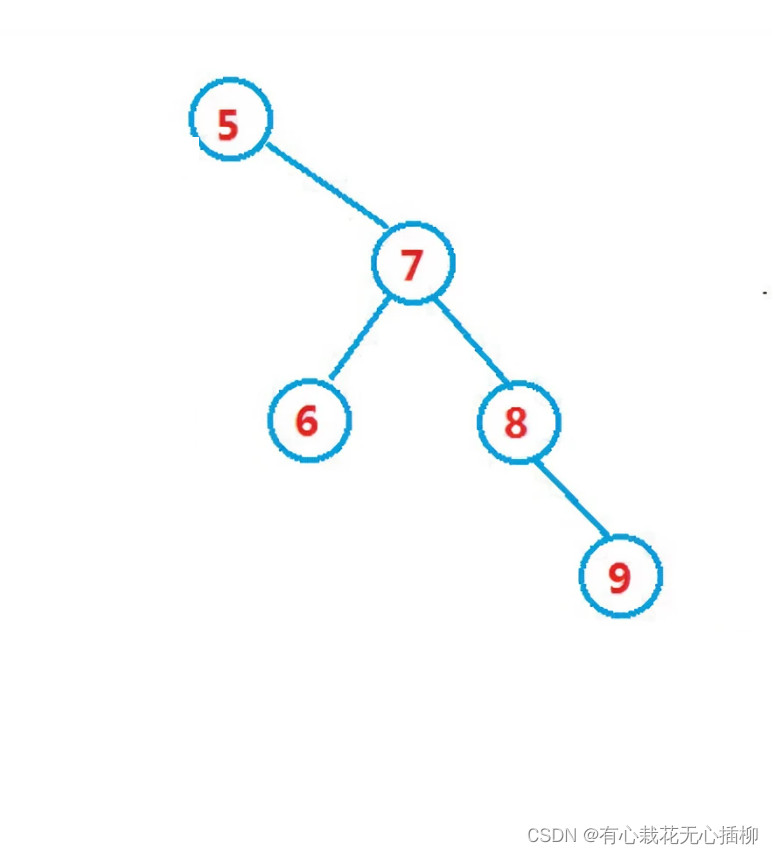
如图,我们要删除8这个结点,肯定是不能直接删除,因为它还有一个孩子,此时让8的父节点领养这个孩子即可。
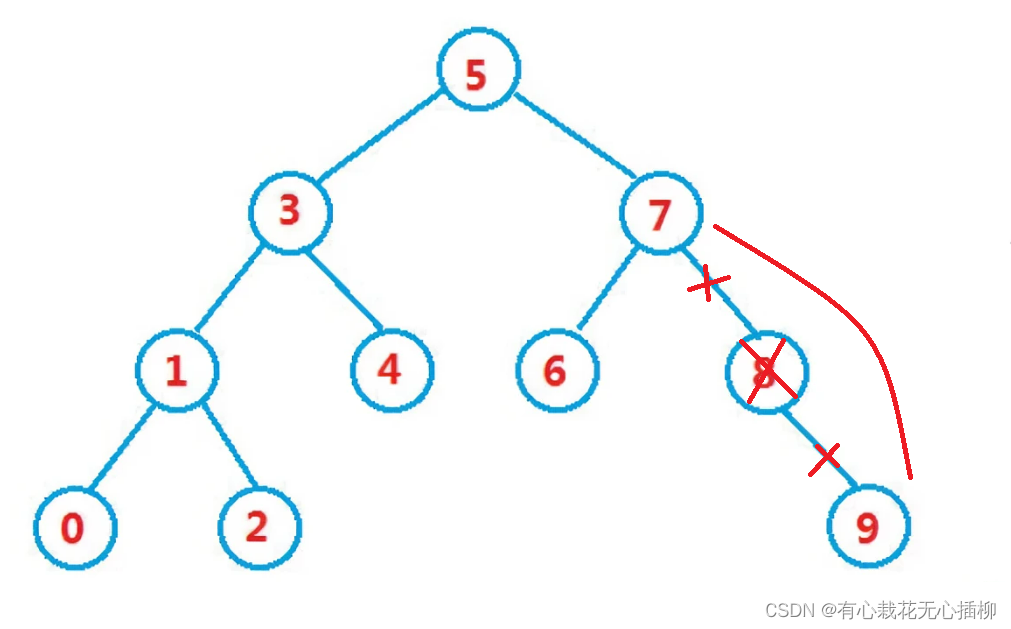
3.被删除的结点有左右两个孩子
被删除的结点有两个孩子的话,就不能像情况2那样找父节点领养了。
那么我们可以想想二叉搜索树的性质:左结点比当前结点小,右节点比当前结点大,且子树也满足此规则。那么也就是说,左子树的所有元素都比当前结点小,右子树的所有元素都比当前结点大。
那么,如果我此时要删除3这个结点,是不是可以用3的左子树里最大的结点或者3的右子树里最小的结点替代掉3。
得益于二叉搜索树这种特殊的性质,很容易验证得到:是可以的。
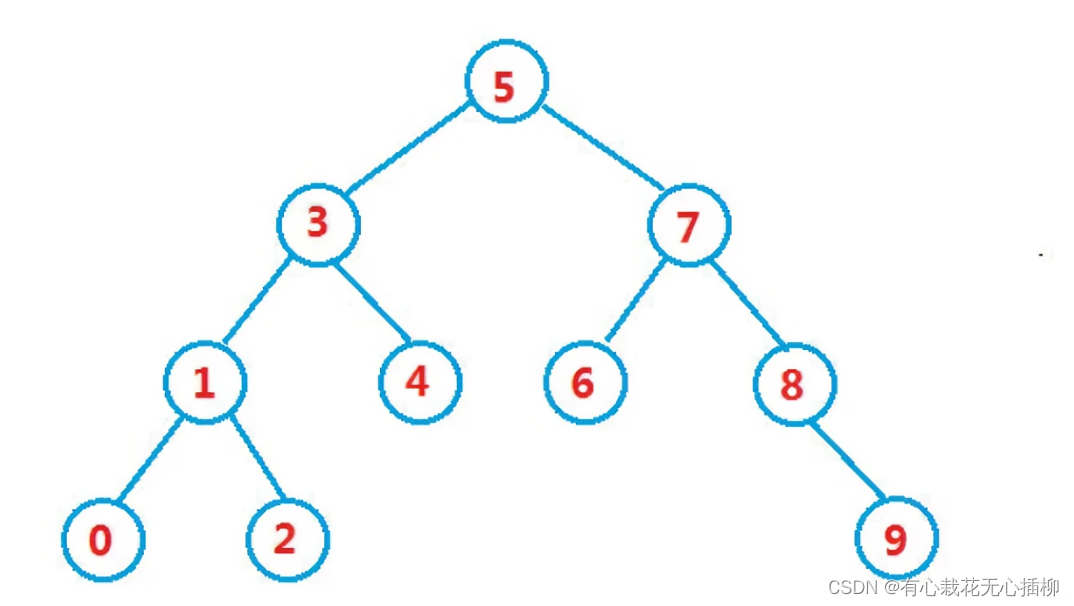
3结点左子树的最大值替换3
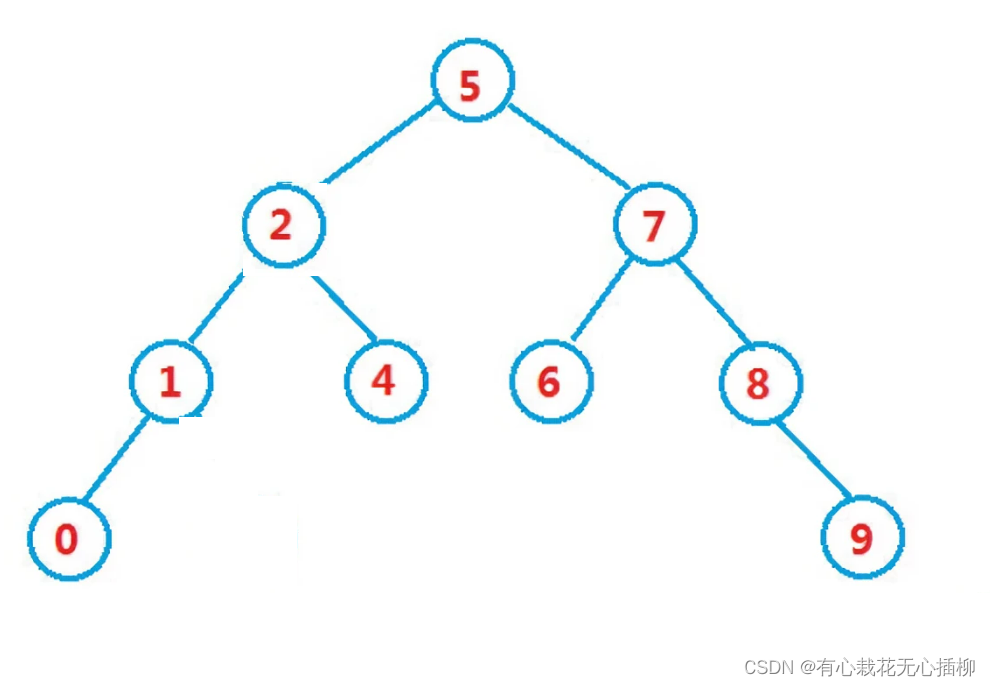
3结点右子树的最小值替换3
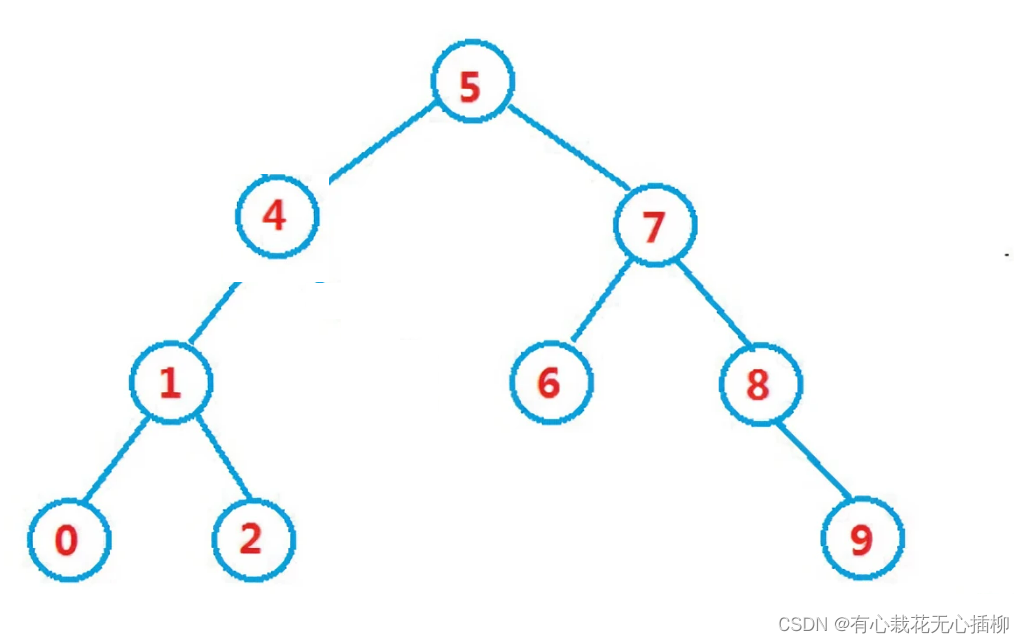
4.1 代码的一些细节分析
我们先假设已经找到了要删除的结点,为cur
先来看情况1和情况2,如果是叶结点直接删除和如果要删除的结点只有一个孩子,就找父节点领养该孩子。
那么可以统一处理,把叶节点链接的nullptr也看作孩子。那么就统一成左为空和右为空的情况了。
这里要处理这两种情况
1.如果要删除的是根结点的话,这个根结点在这里肯定只有左子树或者右子树,我们直接拿根节点的下一个非空结点当根结点即可。
2.如果不是非根结点,直接按照上面的规则即可,记录要删除结点的父节点,然后领养该结点的孩子
2.1 左为空的情况,如果要删除9结点的话,那么让parent->right = cur->right即可
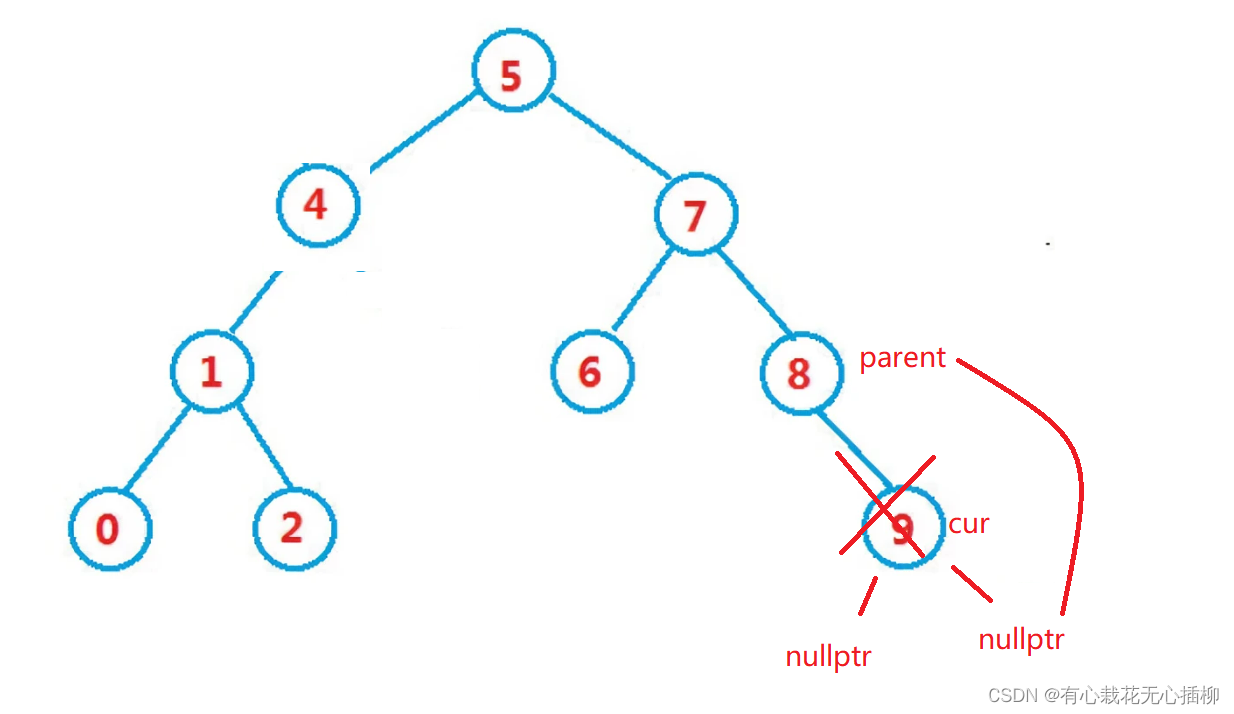
或者是删除8结点的话,也是让parent->right = cur->right
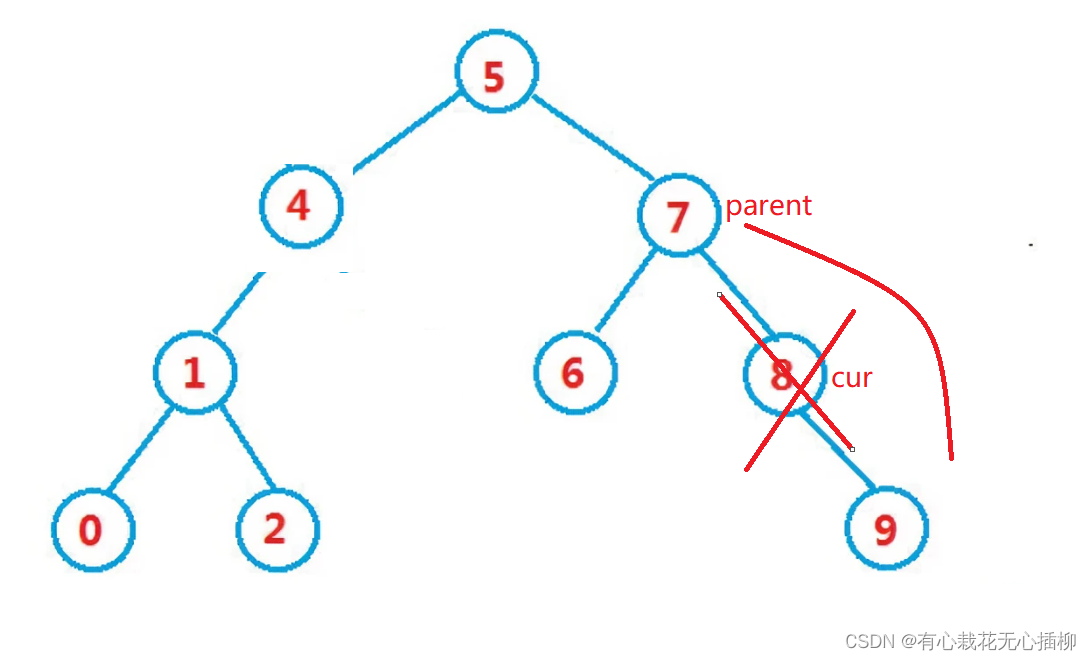
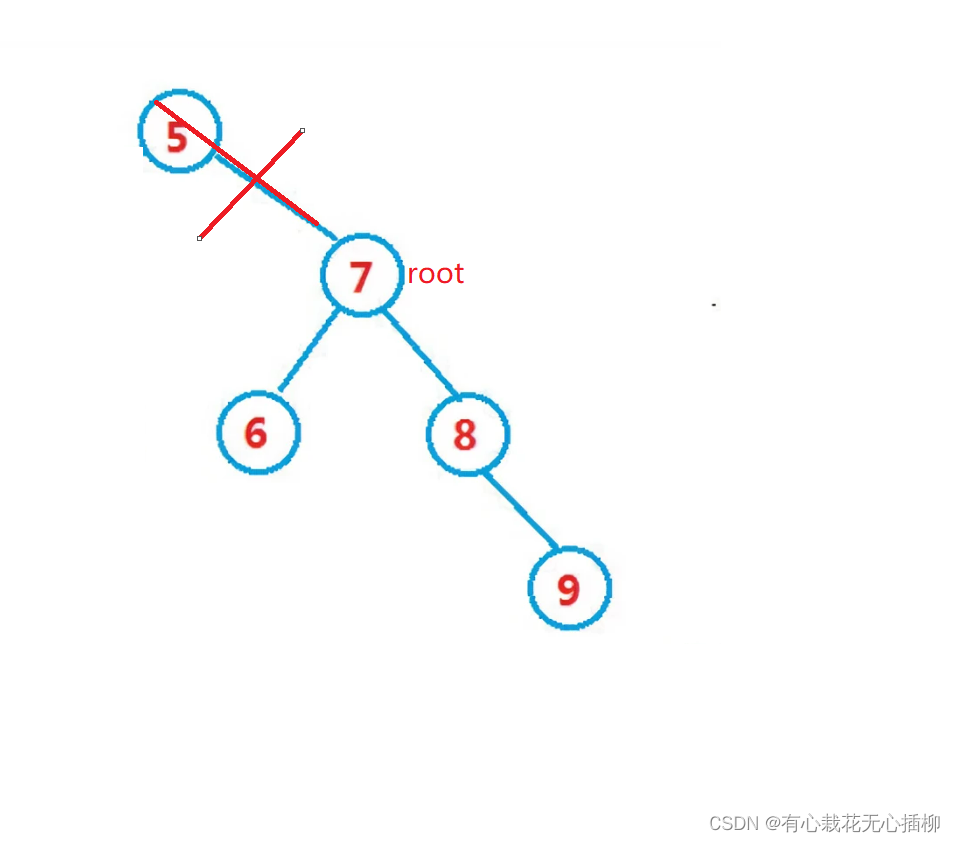
2.2 右为空的情况,我们要删除7这个结点,让parent->right = cur->left
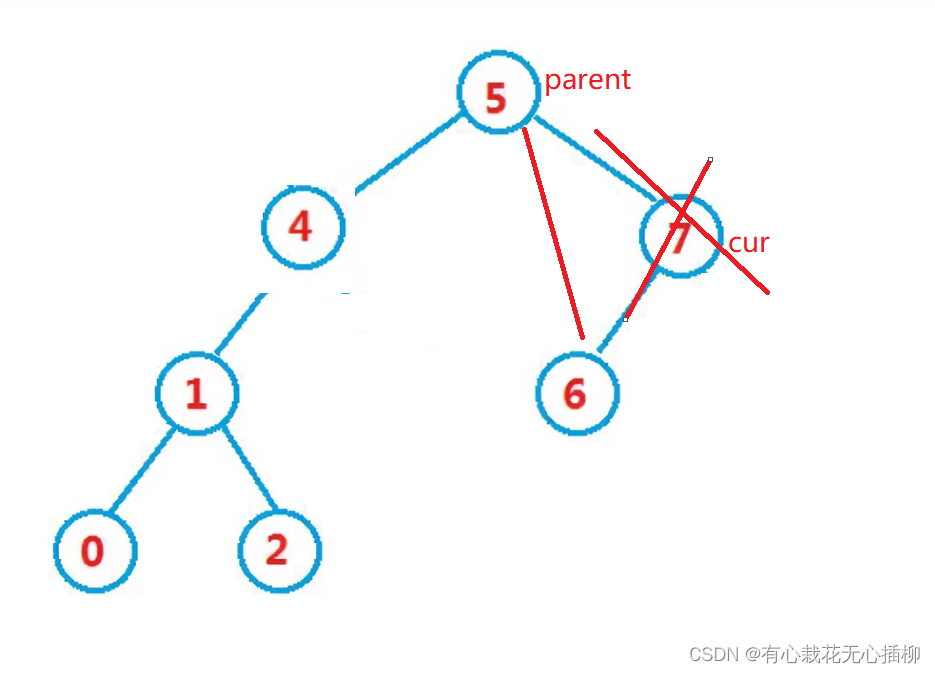
注意:需要判断cur是parent的左节点还是右节点
if (cur->left == nullptr)//如果cur右不为空
{
if (cur == root)//如果要删除的结点是根
{
root = cur->right;//直接用根的右结点替换根
}
else//如果要删除的结点不是根
{
if (parent->left == cur)//记录的父节点的左节点是当前要删除的结点
{
parent->left = cur->right;//直接让父节点领养
}
else//记录的父节点的右结点是当前要删除的结点
{
parent->right = cur->right;//直接让父节点领养
}
}
delete cur;//删除cur
}
else if (cur->right == nullptr)//右为空同理
{
if (cur == root)
{
root = cur->left;
}
else
{
if (parent->left == cur)
{
parent->left = cur->left;
}
else
{
parent->right = cur->left;
}
}
delete cur;
}
我们最后来看一下情况3,要删除的结点有左右两子树
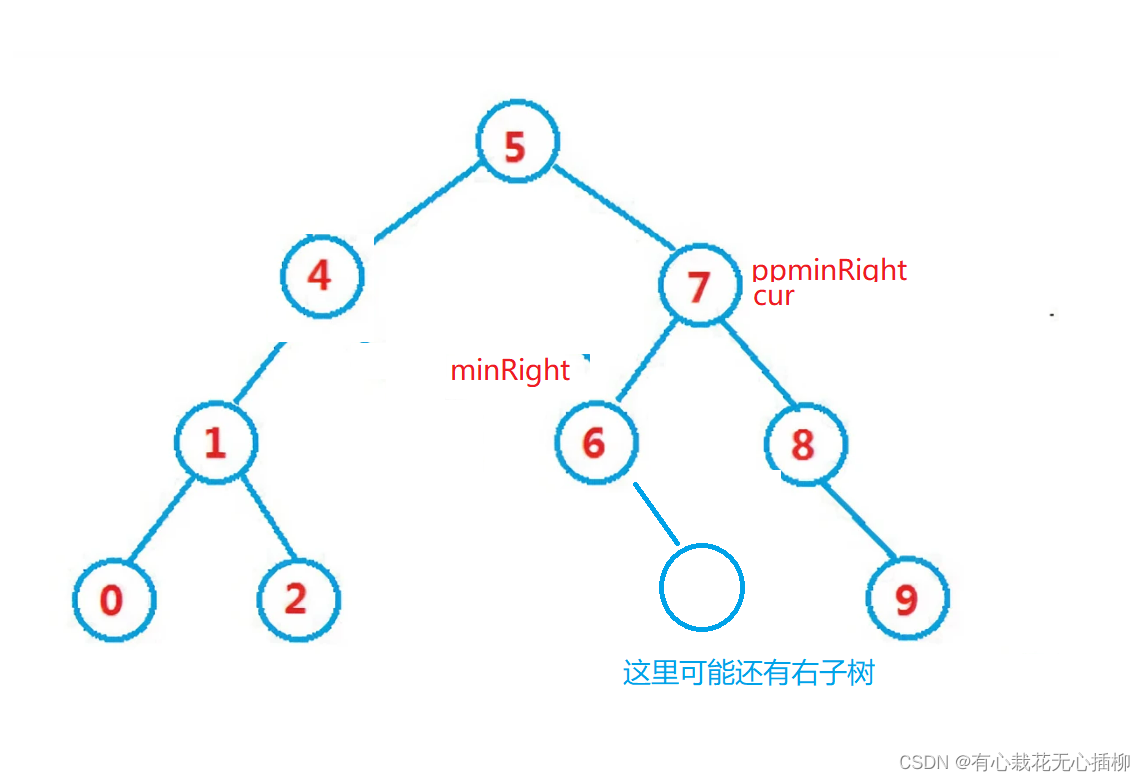
我们这里采用右子树的最小结点要替换要删除的结点。那么我们需要找到该结点右子树的最小结点。
Node* ppminRight = cur;//cur为要删除的结点,记录最小结点的父节点
Node* minRight = cur->right;//找cur右子树最小的结点
while (minRight->left)//如果minRight的左节点为空就停下
{
ppminRight = minRight;
minRight = minRight->left;
}
我们来看以下这两种情况
1.要删除7结点,此时minRight是存在的,minRight要替换掉cur,但是minRight还有自己的右子树,此时我们让父结点领养即可,ppminRight->left = minRight->right
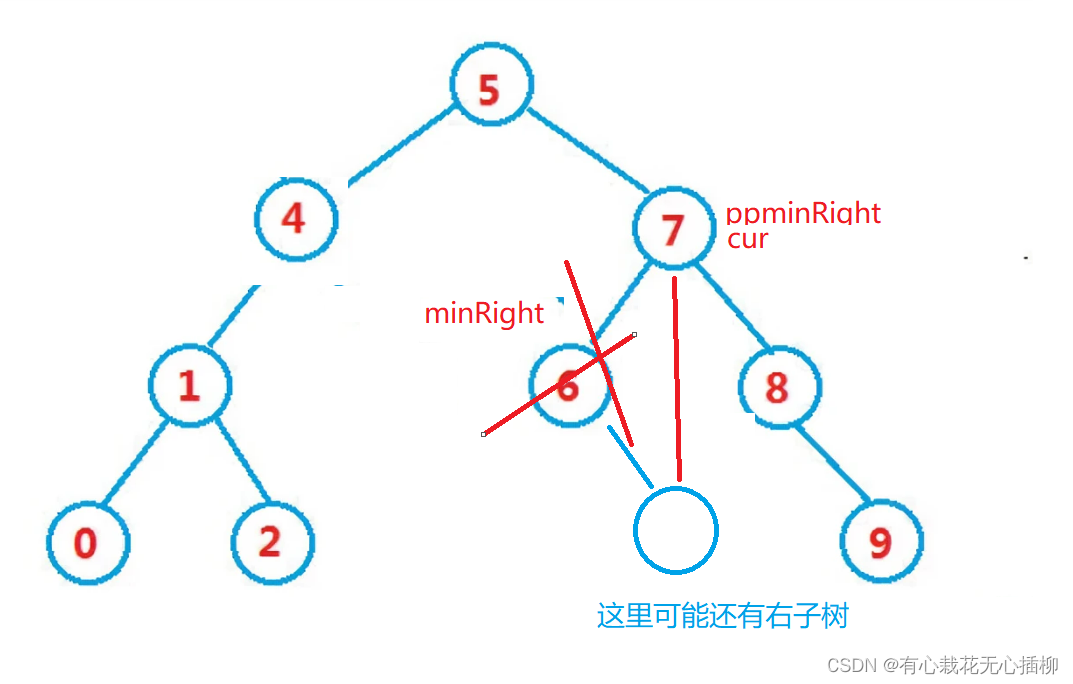
2.要删除5结点,此时minRight为7,是5这个结点的右子树的最小值,也是ppminRight的右节点
此时让ppminRight->right = minRight->right
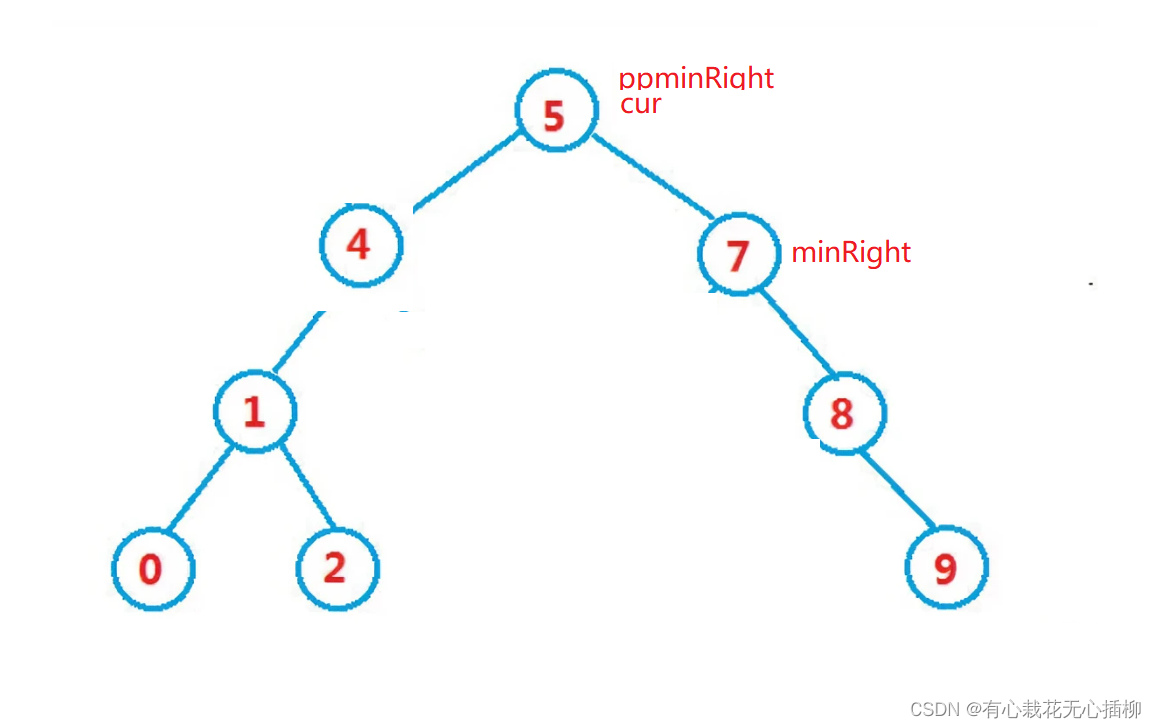
cur->_key = minRight->_key;//找到了以后就直接交换值即可
if (ppminRight->left == minRight)//判断minRight是否ppminRight的左子树
{
ppminRight->left = minRight->right;//ppminRight领养minRight的右子树
}
else//否则就就让ppminRight领养minRight的右子树
{
ppminRight->right = minRight->right;
}
delete minRight;
完整代码:
bool erase(const K& key)
{
Node* parent = nullptr;
Node* cur = root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->right;
}
else if (cur->_key > key)
{
cur = cur->left;
}
else
{
if (cur->left == nullptr)
{
if (cur == root)
{
root = cur->right;
}
else
{
if (parent->left == cur)
{
parent->left = cur->right;
}
else
{
parent->right = cur->right;
}
}
delete cur;
}
else if (cur->right == nullptr)
{
if (cur == root)
{
root = cur->left;
}
else
{
if (parent->left == cur)
{
parent->left = cur->left;
}
else
{
parent->right = cur->left;
}
}
delete cur;
}
else
{
Node* ppminRight = cur;
Node* minRight = cur->right;
while (minRight->left)
{
ppminRight = minRight;
minRight = minRight->left;
}
cur->_key = minRight->_key;
if (ppminRight->left == minRight)
{
ppminRight->left = minRight->right;
}
else
{
ppminRight->right = minRight->right;
}
delete minRight;
}
return true;
}
}
return false;
}
5 总结
以上就是二叉树搜索树的插入、查找、删除操作。完整的代码如下,读者可自行测试。
如有错误,欢迎指出。
https://gitee.com/F_F_G/structure/blob/master/BinaryTree/BinaryTree/BTree.h