例题来源：侯忠生教授的《无模型自适应控制：理论与应用》（2013年科学出版社）。

👉对应书本 4.4 单输入单输出系统(SISO)全格式动态线性化(FFDL)的无模型自适应控制(MFAC)

上两篇博客分别介绍了基于紧格式和偏格式动态线性化的无模型自适应控制：
【MFAC】基于紧格式动态线性化的无模型自适应控制（Matlab代码）

【MFAC】基于偏格式动态线性化的无模型自适应控制（Matlab代码）

全格式动态线性化(FFDL)的PPD相对偏格式动态线性化(PFDL)控制变量增多，能够更好地模拟系统的复杂动态。

例题4.7

1.题目要求

在CFDL中，线性化长度常数 L=1，步长因子仅有1个($\rho$)，伪偏导数(PPD) ${\varphi }_c$ 是一个数；在PFDL中，PPD ${\varphi }_{p,L}$ 是一个 L 维的向量，步长因子增多(${\rho }_1,{\rho }_2,...,{\rho }_{L_y}$)；而在FFDL中，PPD ${\varphi }_{f,L_y,L_u}$ 是一个 $L_y+L_u$ 维的向量，步长因子更多(${\rho }_1,{\rho }_2,...,{\rho }_{L_y+L_u}$)。

2.matlab代码

clear all; clc;

%% 控制器参数
Lu=2; % 输入阶数
Ly=1; % 输出阶数
eta=0.2; % 伪偏导步长
miu=1; % 伪偏导权重
rho=0.7; % 控制律步长 rho1=rho2=rho3=0.7
lamda=7; % 控制律权重
epsilon=1e-5; % 伪偏导重置阈值
N=700; %采样点

%% 初值
y(1:3)=0; y(4)=1; y(5)=0.2; y(6)=0;
u(1:6)=0; u(5)=0.5;
for i=1:Ly
    dy(5,i)=y(5-i+1)-y(5-i);
end
for i=1:Lu
    du(5,i)=u(5-i+1)-u(5-i);
end

%% 期望值
for k=1:N+1
    if k<=490
        yd(k)=0.4*(-1)^round(k/50);
    else
        yd(k)=0.1+0.1*(-1)^round(k/50);
    end
end
figure(1)
plot(yd,'k');
hold on;

%% 控制器伪偏导数初值
% phi_{f,L_y,L_u}(k) = [phi_1(k), phi_2(k),...,phi_{L_y}(k),phi_{L_y+1}(k),...,,phi_{L_y+L_u}(k)]^T
% phi(k,i):第1个参数是k(1~N)，第2个参数是i(1~L_y+L_u)，先是1~L_y，再到L_y+1~L_u
phi(1,:)=[-2 0.5 0.2];
phi(2,:)=phi(1,:); phi(3,:)=phi(1,:); phi(4,:)=phi(1,:); phi(5,:)=phi(1,:);

for k=6:N
    %% 伪偏导更新
    % Delta{H_{L_y,L_u}} = [Delta{y(k)}, Delta{y(k-1)},...,Delta{y(k-(L_y-1))},Delta{u(k)}, Delta{u(k-1)},...,Delta{u(k-(L_u-1))}]^T
    % [dy(k-1,1:Ly) du(k-1,1:Lu)]:前面是y，后面是u
    % du(k,i):第1个参数是k(1~N)，第2个参数是i(1~L_u)
    % dy(k,i):第1个参数是k(1~N)，第2个参数是i(1~L_y)
    if Ly<=0
        phi(k,:)=phi(k-1,:)+eta*(y(k)-y(k-1)-phi(k-1,:)*[du(k-1,1:Lu)]')*du(k-1,1:Lu)/(miu+[du(k-1,1:Lu)]*du(k-1,1:Lu)');
    else
        phi(k,:)=phi(k-1,:)+eta*(y(k)-y(k-1)-phi(k-1,:)*[dy(k-1,1:Ly) du(k-1,1:Lu)]')*[dy(k-1,1:Ly) du(k-1,1:Lu)]/(miu+[dy(k-1,1:Ly) du(k-1,1:Lu)]*[dy(k-1,1:Ly) du(k-1,1:Lu)]');
    end
    % 伪偏导重置
    if abs(phi(k,1+Ly))<=epsilon | abs(dy(k-1,1:Ly))<= epsilon | sign(phi(k,1+Ly))~=sign(phi(1,1+Ly))
        phi(k,1+Ly)=phi(1, 1+Ly);
    end
    phi(6,:)=phi(5,:);
    
    %% 控制律更新
    for i=1:Ly
        dy(k,i)=y(k-i+1)-y(k-i);
    end
    
    if Ly<=0
        u(k) = u(k-1)+rho*phi(k,1+Ly)*(yd(k+1)-y(k)-phi(k,Ly+2:Ly+Lu)*du(k-1,2:Lu)')/(lamda+phi(k,1+Ly).^2);       
    else
        u(k) = u(k-1)+rho*phi(k,1+Ly)*(yd(k+1)-y(k)-phi(k,1:Ly)*dy(k,:)'-phi(k,Ly+2:Ly+Lu)*du(k-1,1:Lu-1)')/(lamda+phi(k,1+Ly).^2); 
    end
    
    for i=1:Lu
        du(k,i)=u(k-i+1)-u(k-i);
    end
    
    %% 系统函数
    y(k+1)=(-0.9*y(k)+(4*round(k/100)+sin(k/100)+1)*u(k))/(1+y(k)^2);
    error(k+1)=yd(k+1)-y(k+1);
end

%% 画图
figure(1)
plot(y,'--r');
xlim([0 700]); ylim([-1 1]);
xlabel('time'); ylabel('tracking performance');
legend('y*(k)', 'FFDL-MFAC');
title('FFDL-MFAC tracking performance');

figure(2)
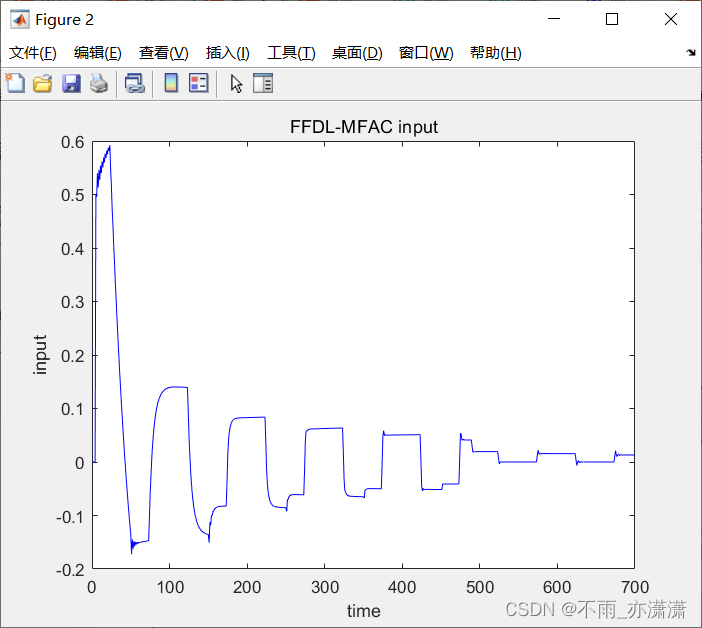
plot(u,'b');
xlabel('time'); ylabel('input');
title('FFDL-MFAC input');

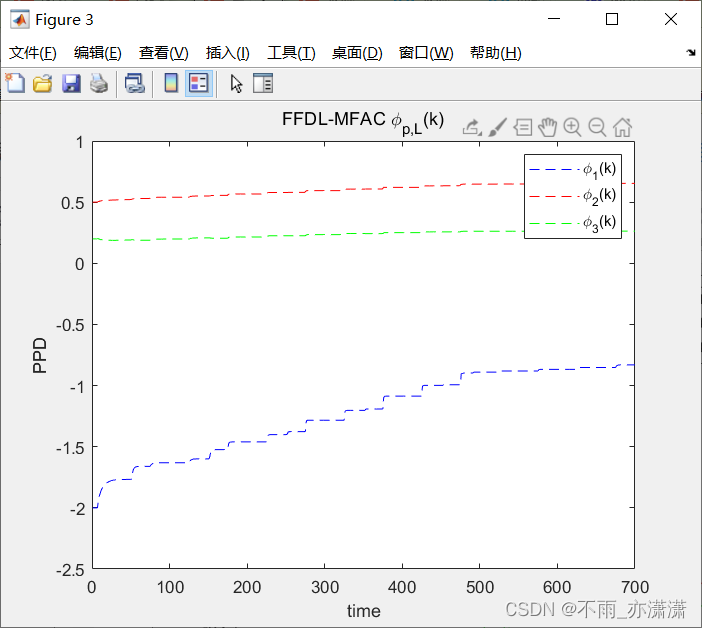
figure(3)
plot(phi(:,1),'b--');hold on;
plot(phi(:,2),'r--');hold on;
plot(phi(:,3),'g--');
xlabel('time'); ylabel('PPD');
legend('\phi_1(k)','\phi_2(k)','\phi_3(k)');
title('FFDL-MFAC \phi_{p,L}(k)');

figure(4)
plot(error);
xlabel('time'); ylabel('tracking error');
title('FFDL-MFAC tracking error')

3.运行结果

跟踪性能

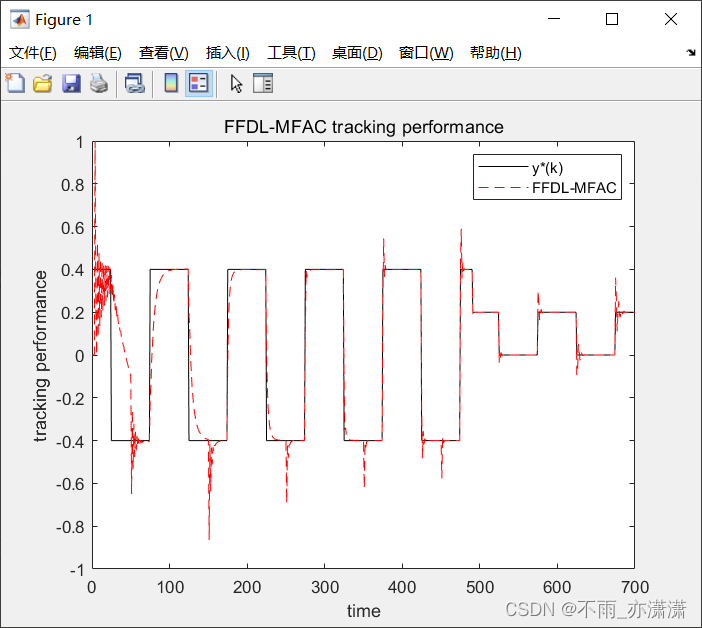
控制输入

PPD估计

跟踪误差