文章目录

双周赛103
- [6406. K 个元素的最大和](https://leetcode.cn/problems/maximum-sum-with-exactly-k-elements/)
- - 模拟
- [6405. 找到两个数组的前缀公共数组](https://leetcode.cn/problems/find-the-prefix-common-array-of-two-arrays/)
- - 模拟
- [6403. 网格图中鱼的最大数目](https://leetcode.cn/problems/maximum-number-of-fish-in-a-grid/)
- - 本质是网格图求连通块大小
- 🎉[6404. 将数组清空](https://leetcode.cn/problems/make-array-empty/)
- - 树状数组

双周赛103

题解参考：小样肖恩：https://leetcode.cn/circle/discuss/KAtdoc/

6406. K 个元素的最大和

难度简单0

给你一个下标从 0 开始的整数数组 nums 和一个整数 k 。你需要执行以下操作恰好 k 次，最大化你的得分：

从 nums 中选择一个元素 m 。
将选中的元素 m 从数组中删除。
将新元素 m + 1 添加到数组中。
你的得分增加 m 。

请你返回执行以上操作恰好 k 次后的最大得分。

示例 1：

输入：nums = [1,2,3,4,5], k = 3
输出：18
解释：我们需要从 nums 中恰好选择 3 个元素并最大化得分。
第一次选择 5 。和为 5 ，nums = [1,2,3,4,6] 。
第二次选择 6 。和为 6 ，nums = [1,2,3,4,7] 。
第三次选择 7 。和为 5 + 6 + 7 = 18 ，nums = [1,2,3,4,8] 。
所以我们返回 18 。
18 是可以得到的最大答案。

示例 2：

输入：nums = [5,5,5], k = 2
输出：11
解释：我们需要从 nums 中恰好选择 2 个元素并最大化得分。
第一次选择 5 。和为 5 ，nums = [5,5,6] 。
第二次选择 6 。和为 6 ，nums = [5,5,7] 。
所以我们返回 11 。
11 是可以得到的最大答案。

提示：

1 <= nums.length <= 100
1 <= nums[i] <= 100
1 <= k <= 100

模拟

题意:每次取一个数，将其作为得分，并对其进行增大 1的操作，进行k次，求总得分最大值。

显然每次取最大值肯定是最好的，因此数组中唯一重要的是最大值 m。因为每次的得分以1为公差依次递增，因此计算一个首项为 m，公差为1，项数为k的等差数列的和即可

时间复杂度为 O(n)，来自于求数组最大值

Java

class Solution {
    public int maximizeSum(int[] nums, int k) {
        Arrays.sort(nums);
        int max = nums[nums.length - 1];
        int res = 0;
        while(k-- > 0){
            res += max;
            max++;
        }
        return res;
    }
}

python

class Solution:
    def maximizeSum(self, nums: List[int], k: int) -> int:
        m = max(nums)
        ans = 0
        while k > 0:
            ans += m
            m += 1
            k -= 1
        return ans
# 推公式：一行代码
class Solution:
    def maximizeSum(self, nums: List[int], k: int) -> int:
        # 推公式：假设数组最大值为m，累加k次
        #   答案就是：m + (m+1) + (m+2) + ... + (m + k - 1)
        #   ==> (m + m + k - 1)*k / 2【(首项+尾项)*项数 / 2：等差数列的前n项和： Sn=[n(A1+An)]/2】
        return (2 * max(nums) + k-1) * k // 2;

6405. 找到两个数组的前缀公共数组

难度中等0

给你两个下标从 0 开始长度为 n 的整数排列 A 和 B 。

A 和 B 的 前缀公共数组 定义为数组 C ，其中 C[i] 是数组 A 和 B 到下标为 i 之前公共元素的数目。

请你返回 A 和 B 的 前缀公共数组 。

如果一个长度为 n 的数组包含 1 到 n 的元素恰好一次，我们称这个数组是一个长度为 n 的排列。

示例 1：

输入：A = [1,3,2,4], B = [3,1,2,4]
输出：[0,2,3,4]
解释：i = 0：没有公共元素，所以 C[0] = 0 。
i = 1：1 和 3 是两个数组的前缀公共元素，所以 C[1] = 2 。
i = 2：1，2 和 3 是两个数组的前缀公共元素，所以 C[2] = 3 。
i = 3：1，2，3 和 4 是两个数组的前缀公共元素，所以 C[3] = 4 。

示例 2：

输入：A = [2,3,1], B = [3,1,2]
输出：[0,1,3]
解释：i = 0：没有公共元素，所以 C[0] = 0 。
i = 1：只有 3 是公共元素，所以 C[1] = 1 。
i = 2：1，2 和 3 是两个数组的前缀公共元素，所以 C[2] = 3 。

提示：

1 <= A.length == B.length == n <= 50
1 <= A[i], B[i] <= n
题目保证 A 和 B 两个数组都是 n 个元素的排列。

模拟

java

class Solution {
    public int[] findThePrefixCommonArray(int[] A, int[] B) {
        int n = A.length;
        int[] res = new int[n];
        int[] cnta = new int[n+1];
        int[] cntb = new int[n+1];
        int presum = 0;
        for(int i = 0; i < n; i++){
            cnta[A[i]]++;
            cntb[B[i]]++;
            if(A[i] != B[i]){
                if(cntb[A[i]] > 0) presum += 1;
                if(cnta[B[i]] > 0) presum += 1;   
            }else{
                if(cntb[A[i]] > 0) presum += 1;
            }
            res[i] = presum;
        }
        return res;
        
    }
}

由于两个数组都是1到 n 的排列，前缀公共部分种的任意一个数，一定在 A,B 中分别出现一次，即出现两次。因此在一个数出现两次时，前缀公共数字数量增加了 1，使用这一性质更新即可。

时间复杂度为O(n)，来源于遍历数组

class Solution:
    def findThePrefixCommonArray(self, A: List[int], B: List[int]) -> List[int]:
        n, presum = len(A), 0
        ans = []
        cnt = [0] * (n+1)
        for x, y in zip(A, B):
            cnt[x] += 1
            if cnt[x] == 2: 
                presum += 1 # 不要在 cnt[y] += 1 后进行，否则 x = y 的情况下分别计数，会多算
            cnt[y] += 1
            if cnt[y] == 2:
                presum += 1
            ans.append(presum)
        return ans

6403. 网格图中鱼的最大数目

难度困难1

给你一个下标从 0 开始大小为 m x n 的二维整数数组 grid ，其中下标在 (r, c) 处的整数表示：

如果 grid[r][c] = 0 ，那么它是一块陆地。
如果 grid[r][c] > 0 ，那么它是一块水域，且包含 grid[r][c] 条鱼。

一位渔夫可以从任意水域格子 (r, c) 出发，然后执行以下操作任意次：

捕捞格子 (r, c) 处所有的鱼，或者
移动到相邻的水域格子。

请你返回渔夫最优策略下，最多可以捕捞多少条鱼。如果没有水域格子，请你返回 0 。

格子 (r, c) 相邻的格子为 (r, c + 1) ，(r, c - 1) ，(r + 1, c) 和 (r - 1, c) ，前提是相邻格子在网格图内。

示例 1：

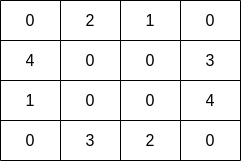
输入：grid = [[0,2,1,0],[4,0,0,3],[1,0,0,4],[0,3,2,0]]
输出：7
解释：渔夫可以从格子 (1,3) 出发，捕捞 3 条鱼，然后移动到格子 (2,3) ，捕捞 4 条鱼。

示例 2：

输入：grid = [[1,0,0,0],[0,0,0,0],[0,0,0,0],[0,0,0,1]]
输出：1
解释：渔夫可以从格子 (0,0) 或者 (3,3) ，捕捞 1 条鱼。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 10
0 <= grid[i][j] <= 10

本质是网格图求连通块大小

对于每一个水域构成的连通块，最多捕捞的鱼的总数为这个连通块里鱼的数量的总和。因此我们只需要对于每一个连通块查看总鱼数量即可。这个可以用深度/广度优先搜索或并查集直接解决。时间复杂度O(nm)。

java（DFS）

在遍历每一个连通块时，可以将遍历过的位置值设置为0，这样就不用开vis数组了

class Solution {
    int[][] dirts = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
    int[][] grid;
    int n, m;
    public int findMaxFish(int[][] grid) {
        int res = 0;
        n = grid.length; 
        m = grid[0].length;
        this.grid = grid;
        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++)
                    res = Math.max(res, dfs(i, j));
        }
        return res;
    }

    public int dfs(int i, int j){
        if(i < 0 || i >= n || j < 0 || j >= m || grid[i][j] == 0)
            return 0;
        int result = grid[i][j];
        grid[i][j] = 0;
        for(int[] d : dirts){
            int x = i + d[0], y = j + d[1];
            result += dfs(x, y);
        }
        return result;
    }
}

python

class Solution:
    def findMaxFish(self, grid: List[List[int]]) -> int:
        n, m = len(grid), len(grid[0])
        ans = 0

        def dfs(i, j: int) -> int:
            res = grid[i][j]
            grid[i][j] = 0
            for x, y in (i + 1, j), (i - 1, j), (i, j - 1), (i, j + 1): 
                if 0 <= x < n and 0 <= y < m and grid[x][y]:
                    res += dfs(x, y)
            return res

        for i in range(n):
            for j in range(m):
                if grid[i][j] > 0:
                    tot = dfs(i, j)
                    ans = max(ans, tot)
        return ans

更短更优雅的网格图DFS模板:python

class Solution:
    def findMaxFish(self, grid: List[List[int]]) -> int:
        n, m = len(grid), len(grid[0])
        ans = 0

        def dfs(i, j: int) -> int:
            if i < 0 or i >= n or j < 0 or j >= m or grid[i][j] == 0:
                return 0
            res = grid[i][j]
            grid[i][j] = 0
            for x, y in (i + 1, j), (i - 1, j), (i, j - 1), (i, j + 1): 
                    res += dfs(x, y)
            return res

        return max(max(dfs(i, j) for j in range(m)) for i in range(n))

🎉6404. 将数组清空

难度困难2

给你一个包含若干 互不相同 整数的数组 nums ，你需要执行以下操作 直到****数组为空 ：

如果数组中第一个元素是当前数组中的 最小值 ，则删除它。
否则，将第一个元素移动到数组的末尾。

请你返回需要多少个操作使 nums 为空。

示例 1：

输入：nums = [3,4,-1]
输出：5

Operation	Array
1	[4, -1, 3]
2	[-1, 3, 4]
3	[3, 4]
4	[4]
5	[]

示例 2：

输入：nums = [1,2,4,3]
输出：5

Operation	Array
1	[2, 4, 3]
2	[4, 3]
3	[3, 4]
4	[4]
5	[]

示例 3：

输入：nums = [1,2,3]
输出：3

Operation	Array
1	[2, 3]
2	[3]
3	[]

提示：

1 <= nums.length <= 105
-109 <= nums[i] <= 109
nums 中的元素 互不相同 。

题解：小羊肖恩 https://leetcode.cn/u/yawn_sean/

首先，我们肯定不能直接执行题目中给出的操作，否则时间复杂度将达到操作的数量。那么，我们应该在原数组中考虑删除操作和移动操作分别意味着什么。

我们考虑一个指针，在原数组中进行移动，且每次移动一个单位。那么“第一个元素移动到末尾”可以刻画为将该指针移动到下一个还在数组中的数字位置上，“删除”可以刻画为将某一个位置置空。

删除的位置顺序是预先给定的，对应位置的数字从小到大。

接下来我们考虑两次删除操作之间的间隔，相当于从某个位置移动到下一个最小值的位置。这两个位置在原数组中的下标是确定的， 因此我们只需要考虑这两点间有多少位置未被置空即可，这相当于一个区间求和，每次可以更新置空情况。 这可以通过线段树或树状数组等实现（可以搜索相关知识）。具体逻辑可见代码注释。

时间复杂度为O(nlogn)，来源于排序还有树状数组等结构的更新

为什么大佬们一眼看出是树状数组呢？

不是一眼看出树状数组，而是要把找两个相邻的最小值之间还有几个数没删掉的问题转变成动态区间和问题，这个转化过程才是最重要的，至于你用什么数据结构求动态区间和是次要的，很多数据结构都能做，最常用的树状数组和线段树(这题比较特殊有序集合也能做)，树状数组容易套板，码量少，常数还比线段树小。所以你才会看到大佬们清一色的树状数组。

树状数组

题解：https://leetcode.cn/problems/make-array-empty/solution/shu-zhuang-shu-zu-mo-ni-pythonjavacgo-by-ygvb/

class Solution:
    """
    转换：
    将第一个元素移动到数组的末尾 
        ==> 用 下标  来标记当前数组的第一个数是谁，然后不断往后移动
            举例 ：2413 ==> 当前下标2 ==> 1324 ==>删除1 ==> 324 ==> 当前下标3
    这个转换是怎么想到的？技巧，相对关系【数字往后移 等价于 用一个下标来模拟】

    删除一个数后，下标自动向右移动一位（这一次操作是免费的）

    我们需要记录每一个数的位置，从小到大删除
    上一个删除的数的下标是 pre， 当前要删除的下标是 i
    因此我们需要思考【从pre移动到i，需要移动多少次？】
    1. 维护中间被删除的数字个数
    ==> 树状数组
        如果pre <= i, 移动次数 i-pre-query(pre,i) 【pre到i，再减去中间删除的个数】
        如果pre > i, 移动次数 n - pre-query(pre,n) + 1【n到1的那一步】 + (i-1) - query(1,i) 【pre到n，再从1到i】 
            简化一下： n - pre + i - (k - query(i, pre-1)) 【树状数组中一共有k个数】
    2. 

    """
    def countOperationsToEmptyArray(self, nums: List[int]) -> int:
        ans = n = len(nums) # 先把 n 计入答案
        t = BIT(n+1) # 树状数组下标从1开始
        pre = 1 # 上一个最小值的位置，初始为 1
        # 根据元素大小对下标进行排序，然后枚举 数的位置 从小到大删除每个数
        ids = sorted(range(n), key = lambda i: nums[i])
        for k, i in enumerate(ids):
            i += 1 # 下标i从1开始
            if pre <= i: # 从 pre 移动到 i，跳过已经删除的数
                ans += i - pre - t.query(pre, i)
            else:
                ans += n - pre + i - (k - t.query(i, pre-1))
            t.inc(i) # 删除i（添加到树状数组中）
            pre = i
        return ans

# 树状数组模板
class BIT:
    def __init__(self, n):
        self.tree = [0] * n

    # 将下标 i 上的数加一
    def inc(self, i: int) -> None:
        while i < len(self.tree):
            self.tree[i] += 1
            i += i & -i

    # 返回闭区间 [1, i] 的元素和
    def sum(self, i: int) -> int:
        res = 0
        while i > 0:
            res += self.tree[i]
            i &= i - 1
        return res

    # 返回闭区间 [left, right] 的元素和
    def query(self, left: int, right: int) -> int:
        return self.sum(right) - self.sum(left - 1)

java

class Solution {
    public long countOperationsToEmptyArray(int[] nums) {
        int n = nums.length;
        Integer[] ids = new Integer[n];
        for(int i = 0; i < n; i++) ids[i] = i;
        Arrays.sort(ids, (i, j) -> nums[i] - nums[j]);

        long ans = n; // 先把n计入答案
        BinaryIndexedTree t = new BinaryIndexedTree(n+1); // 下标从1开始
        int pre = 1;
        for(int k = 0; k < n; k++){
            int i = ids[k] + 1;// 当前要删除的下标，提前+1（下标从1开始）
            if(i >= pre) // 从 pre 移动到 i，跳过已经删除的数
                ans += i - pre - t.RangeSum(pre, i);
            else // 从 pre 移动到 n，再从 1 移动到 i，跳过已经删除的数
                ans += n - pre + i - k + t.RangeSum(i, pre-1);
            t.add(i, 1); // 删除i
            pre = i;
        }
        return ans;
    }
}

// BIT动态维护 arr 的前缀和(注意这里下标是从1开始的)
class BinaryIndexedTree{
    private int n;
    private int[] tree;

    public BinaryIndexedTree(int n){ // 初始化时，要传入n+1
        this.n = n;
        tree = new int[n];
    }
    // 将index位置加上val值 arr[i] += val（注意传进来的index要+1）
    public void add(int index, int val){
        while(index < n){
            tree[index] += val;
            index += index & -index;
        }
    }
    // 查询[1, index]的前缀和（注意传进来的index要+1）
    public int query(int index) {
        int s = 0;
        while (index > 0) {
            s += tree[index];
            index -= index & -index; // n&(~n+1) == n&(-n)
        }
        return s;
    }
	// 返回[left, right]之间的区间和（注意传进来的index要+1）
    public int RangeSum(int left, int right){
        return query(right) - query(left-1);
    }
}