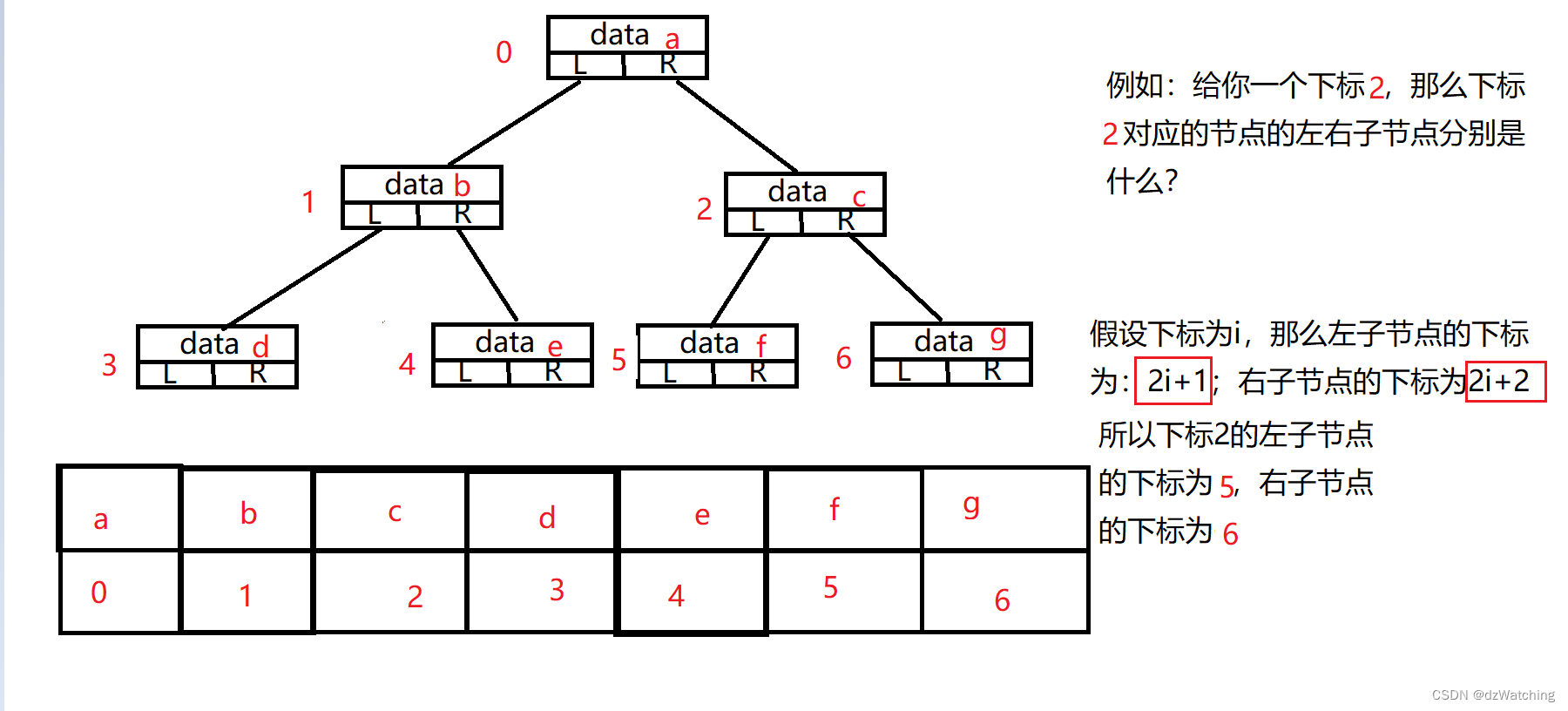
文章目录
- A. TubeTube Feed
- 1、题目
- 2、分析
- 3、代码,
- B. Karina and Array
- 1、题目
- 2、分析
- 3、代码
- C. Bun Lover
- 1、问题
- 2、分析
- (1)观察样例法
- (2)正解推导
- 3、代码
- D. Super-Permutation
- 1、问题
- 2、分析
- (1)观察样例构造
- (2)构造的简单推导
- 3、代码
- E. Making Anti-Palindromes
- 1、问题
- 2、分析
- 3、代码
- F. Gardening Friends
- 1、问题
- 2、分析
- 3、代码
- G1. Magic Triples (Easy Version)
- 1、问题
- 2、分析
- 3、代码
- G2. Magic Triples (Hard Version)
- 1、问题
- 2、分析
- 3、代码
A. TubeTube Feed
A. TubeTube Feed
1、题目
有很多电视节目,每个节目有两个属性,一个是时长 a [ i ] a[i] a[i],一个是娱乐价值 b [ i ] b[i] b[i]。
这些节目按照顺序给出,我们只能选择一个节目进行观看,目的是获得最大的娱乐价值。如果当前节目不想看,则需要花费 1 1 1秒来跳过。
现在需要我们选出最优节目所对的下标。
如果一个都不能看的话,输出 − 1 -1 −1。
2、分析
将节目存入数组中,下标从0开始,则对于第 i i i个节目而言,我们需要等待的时间是 i i i秒,观看的时间是 a [ i ] a[i] a[i]。如果我们选择第 i i i个节目,就要花费 a [ i ] + i a[i]+i a[i]+i秒的时间。只要这个值在规定的 t t t内,就可以选。
基于上述分析,我们只需要选出所有在 t t t时间内的节目,再挑出最大值即可。
3、代码,
#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 1e5 + 10;
void solve()
{
int n, t;
cin >> n >> t;
vector<int>a(n), b(n);
for(auto &x : a)
cin >> x;
for(auto &x : b)
cin >> x;
int ansv = -1 ,pos = -1;
for(int i = 0; i < n; i ++ )
{
if(t >= a[i] + i)
{
if(ansv < b[i])
{
ansv = b[i];
pos = i + 1;
}
}
}
cout << pos << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
B. Karina and Array
B. Karina and Array
1、题目
给定一个数组,我们人为规定顺序,规定好顺序后,相邻数字相乘得到一个新数组,再从新数组中挑出一个最大值。我们要做的就是输出这个最大值。
2、分析
很明显,如果是两个正数,我们选择最大的两个相乘。如果是两个负数,我们选择最小的两个相乘。
所以,我们只需要找到最大的两个数和最小的两个数,分别相乘后比较输出最大值即可。
不要忘了开 l o n g l o n g long long longlong,最大值为 1 0 9 ∗ 1 0 9 10^9*10^9 109∗109, i n t int int存不下。
3、代码
#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f3f3f3f3f
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 1e5 + 10;
void solve()
{
int n;
cin >> n;
vector<int>a(n);
for(int i = 0; i < n; i ++ )
cin >> a[i];
sort(a.begin(), a.end());
cout << max(a[0] * a[1], a[n - 1] * a[n - 2]) << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
C. Bun Lover
C. Bun Lover
1、问题
给一个肉桂卷,即下图。要求我们出下列图案中棕色线条的长度。
其中,下列图案最外围的正方形边长是
n
n
n,中心的最短线段是
1
1
1。
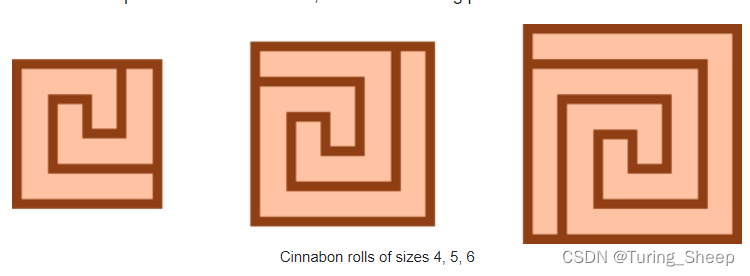
2、分析
(1)观察样例法
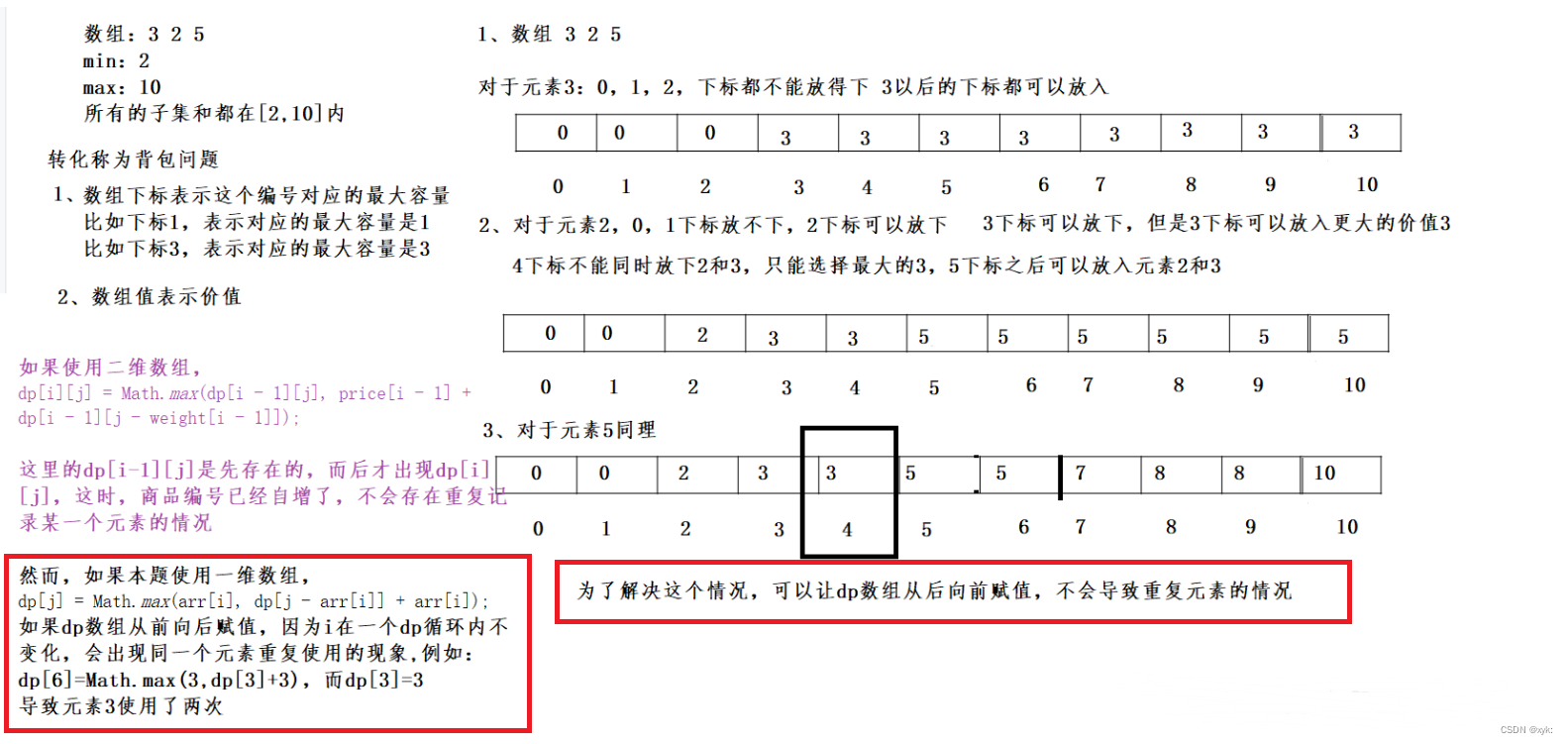
观察样例,我们发现,所有的样例都是 ( n + 1 ) 2 + 1 (n+1)^2+1 (n+1)2+1。所以直接输出这个公式即可,不要忘了开 l o n g l o n g longlong longlong。
(2)正解推导

将棕色线条按上述三种颜色分类:
黄色线:
l
e
n
1
=
1
len1 = 1
len1=1
蓝色线:

l
e
n
2
=
(
n
+
1
)
∗
(
n
)
2
len2=\frac{(n+1)*(n)}{2}
len2=2(n+1)∗(n)
粉色线:
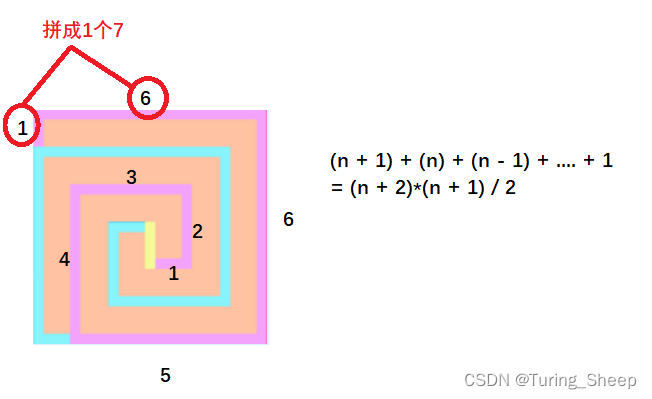
l
e
n
3
=
(
n
+
2
)
∗
(
n
+
1
)
2
len3=\frac{(n+2)*(n+1)}{2}
len3=2(n+2)∗(n+1)
综上:
l
e
n
=
l
e
n
3
+
l
e
n
2
+
l
e
n
1
l
e
n
=
(
n
+
2
)
∗
(
n
+
1
)
2
+
(
n
+
1
)
∗
(
n
)
2
+
1
=
(
2
n
+
2
)
∗
(
n
+
1
)
2
+
1
len=len3+len2+len1\\ len=\frac{(n+2)*(n+1)}{2}+\frac{(n+1)*(n)}{2}+1\\ =\frac{(2n+2)*(n+1)}{2}+1\\
len=len3+len2+len1len=2(n+2)∗(n+1)+2(n+1)∗(n)+1=2(2n+2)∗(n+1)+1
即:
l
e
n
=
(
n
+
1
)
2
+
1
len=(n+1)^2+1
len=(n+1)2+1
3、代码
#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 1e5 + 10;
void solve()
{
int n;
cin >> n;
cout << (n + 1) * (n + 1) + 1 << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
D. Super-Permutation
D. Super-Permutation
1、问题
给定一个排列,我们需要重新排序得到 a [ i ] a[i] a[i],并构造一个前缀和数列 s [ i ] s[i] s[i]。题目中的 b [ i ] b[i] b[i]即 s [ i ] % n s[i]\%n s[i]%n。此时,我们需要判断 b [ i ] + 1 b[i]+1 b[i]+1数组是否是一个排列?如果是,则构造一个 a [ i ] a[i] a[i]数组输出,如果不存在这样的数组,则输出 − 1 -1 −1。
2、分析
(1)观察样例构造
这种题型属于构造题,我们可以直接观察样例,按照样例的样子去构造。比如,我们发现如果排列的和是 n n n的倍数,则最后不存在这样的数列。反之,则存在。
(长度为 n n n的排列是指从 1 1 1到 n n n不重不漏的出现在数组内。)
但是需要特判 1 1 1这种情况,虽然 1 1 1对 1 1 1取模是 0 0 0,但是最终存在答案,即 1 1 1。
在存在的时候,我们只需要仿照最后一个样例构造:
即
n
,
n
−
1
,
2
,
n
−
3
,
4
,
n
−
5....
n,\ \ n-1,\ \ 2,\ \ n-3,\ \ 4,\ \ n-5....
n, n−1, 2, n−3, 4, n−5....
(2)构造的简单推导
假设
n
n
n在
a
a
a数组中的位置是
k
k
k,则
b
k
=
b
k
−
1
+
a
k
=
b
k
−
1
+
n
b_k=b_{k-1}+a_k=b_{k-1}+n
bk=bk−1+ak=bk−1+n
等式两边同时取模:
b
k
m
o
d
n
=
(
b
k
−
1
+
n
)
m
o
d
n
=
b
k
−
1
b_k\ mod\ n = (b_{k-1}+n)mod\ n = b_{k-1}
bk mod n=(bk−1+n)mod n=bk−1
即:
b
k
=
b
k
−
1
b_k=b_{k-1}
bk=bk−1,说明前后元素重复,必定不是排序,所以
n
n
n必须在第一个元素才行。
从上面可得到结论 b [ 1 ] = a [ 1 ] m o d n = 0 b[1]=a[1]mod\ n=0 b[1]=a[1]mod n=0
无论我们如何构造,我们的 a a a数组的最后一个 a [ n ] a[n] a[n]的数值必定是 s u m sum sum,而 s u m = 1 + 2 + 3 + . . + n = n ∗ ( n + 1 ) 2 sum=1+2+3+..+n=\frac{n*(n+1)}{2} sum=1+2+3+..+n=2n∗(n+1)。
当 n n n为奇数的时候, ( n + 1 ) 2 \frac{(n+1)}{2} 2(n+1)是正整数,即 s u m sum sum是 n n n的整数倍,即 b [ n ] = 0 b[n]=0 b[n]=0,此时说明 b [ 1 ] = b [ n ] b[1]=b[n] b[1]=b[n],二者重复,必定不是排列。
所以, n n n为奇数的时候不合法。
当 n n n为偶数的时候合法,构造方法直接仿造最后一个样例即可(构造方案不唯一)。
3、代码
#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 1e5 + 10;
void solve()
{
int n;
cin >> n;
int sum = 0;
sum = (n + 1) * n / 2;
if(n == 1)
{
cout << 1 << endl;
return;
}
if(sum % n == 0)
cout << -1 << endl;
else
{
cout << n << " ";
bool flag = true;
for(int i = 1; i < n; i ++)
{
if(flag)
{
cout << n - i << " ";
flag = false;
}
else
{
cout << i << " ";
flag = true;
}
}
cout << endl;
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
E. Making Anti-Palindromes
E. Making Anti-Palindromes
1、问题
目的是构造反回文串。反回文串满足: s [ i ] ≠ s [ n − i + 1 ] s[i]\neq s[n-i+1] s[i]=s[n−i+1]。如果存在,我们可以选择和其他字符交换位置。
现在给我们一个字符串,我们需要通过最小的操作次数将其调整为一个反回文串。如果存在这样的操作,输出最小的操作次数,如果无法调整为反回文串,输出 − 1 -1 −1。
2、分析
先来分析什么时候不存在答案。
如果字符串长度是奇数,则不满足。当走到中间的字符的时候,首尾指向了同一个字符,故上述等式恒成立。所以奇数的时候不存在答案。
如果某个字符数量超过了一半,也不存在解。
证明:假设字符
x
x
x的出现次数超过了一半,则必定存在
x
x
x和
x
x
x配对的情况,所以这种情况也是无解的。
其余情况均有解,现在考虑如何求出最优解。
我们从两端向中间扫描,统计出所有配对的字符对,并利用一个 m a p map map存储该字符对中的字符,即该字符对出现的次数。
我们想求的是最小的操作次数,即我们要尽量让不同类型的,已经匹配的字符对之间实现字符交换。比如现在存在aa配对,bb配对,我们交换一次,变成ab,ab,使得两组都实现了反回文。相当于1个顶2个。
当我们配对的字符对间实现两两交换后,如果还有剩余,则需要和其余不配对的字符交换。
综合上述,为了答案最小,我们就要让尽可能多的交换实现一个顶俩的效果,即配对字符对之间的交换。
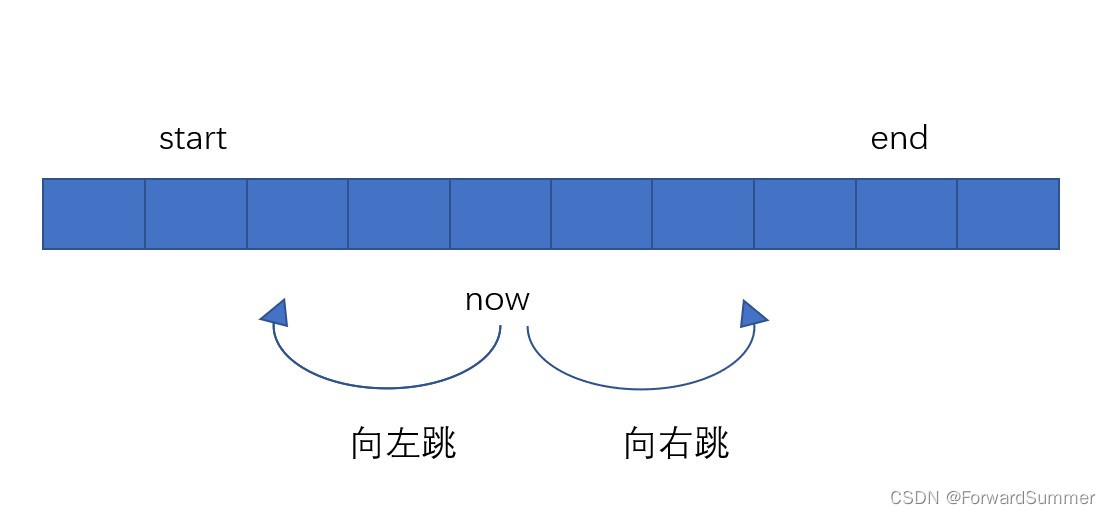
为了方便理解,抽象为下面的数学模型。
我们用不同的颜色代表不同类型的字符对,线段的长度则代表了该类型字符对的个数。
那么最小的操作次数就转化成了对折后,最小的长度。
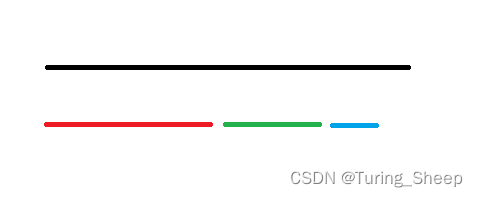
上图的情况中,最小长度就是黑色线的长度。
同时,上图仅仅是最长线段超过一半的情况,如果小于一半呢?就会出现下面的情况。
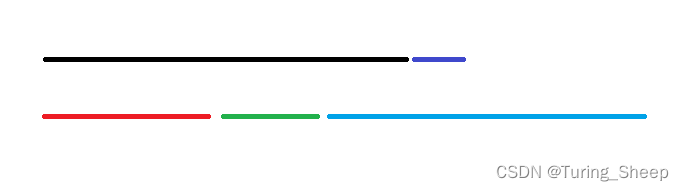
这种情况下,对折后的最小长度又是怎么样的呢?
很明显上图不是最优解。
我们可以做出如下调整:
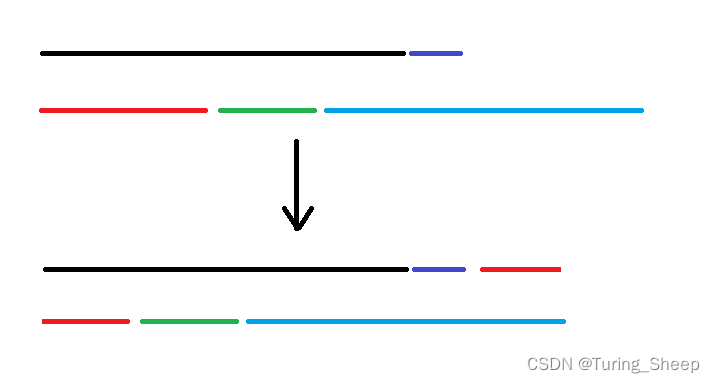
即将下侧的一部分挪到上面去,此时就相当于正好对折。
因此,只要给出上面的情况,我们总能调整为恰好对折的情况(如果是奇数,则有一侧会多出一个)。
如果考虑奇数的问题,此时的最小长度就是 ( s u m + 1 ) / 2 (sum+1)/2 (sum+1)/2,即 s u m / 2 sum/2 sum/2上取整的结果。
综上所述:
我们不妨将最大的同类型的配对字符对数量记作 m a x max max,所有配对的字符对记作 s u m sum sum。
当
m
a
x
<
s
u
m
+
1
2
max<\frac{sum+1}{2}
max<2sum+1的时候,输出
(
s
u
m
+
1
)
/
2
(sum+1)/2
(sum+1)/2。
当
m
a
x
≥
s
u
m
+
1
2
max\geq \frac{sum+1}{2}
max≥2sum+1的时候,输出
m
a
x
max
max。
3、代码
#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 2e5 + 10;
int st[N], n;
char s[N];
void solve()
{
memset(st, 0, sizeof st);
map<char, int>cnt;
cin >> n >> s + 1;
if(n % 2)
{
cout << -1 << endl;
return;
}
for(int i = 1; i <= n; i ++ )
st[s[i] - 'a'] ++;
int maxv = 0;
for(int i = 0; i <= 26; i ++ )
maxv = max(st[i], maxv);
if(maxv > n / 2)
{
cout << -1 << endl;
return;
}
int sum = 0;
for(int i = 1; i <= n / 2; i ++ )
{
if(s[i] == s[n - i + 1])
{
cnt[s[i]]++;
sum++;
}
}
maxv = 0;
for(auto x :cnt)
{
maxv = max(maxv, x.second);
}
if(maxv > (sum + 1) / 2)
cout << maxv <<endl;
else
cout << (sum + 1) / 2 << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
F. Gardening Friends
F. Gardening Friends
1、问题
给定一棵以1为根节点的有根树,距离根最远的点到根的距离为这棵树的价值,同时我们可以花费一定代价让根的子节点当根节点,得到一棵新树。将价值记作
v
a
l
val
val,交换的代价记作
c
o
s
t
cost
cost。
我们要求的就是
v
a
l
−
c
o
s
t
val-cost
val−cost的最大值。
2、分析
这道题考察树的直径。
树的直径即树中两个最远点之间的路径。
树的直径有一个性质,距离任何一个点最远的点是直径两个端点的其中一个。
我们利用这个性质可以求出树的直径,只需要写两次DFS。
第一次DFS可以找到其中一个端点 c c c,再从 c c c出发DFS,得到另一个端点 c c cc cc。
有了上面的前置知识,再来分析这道题。
先看交换的代价,代价等于以 1 1 1为根的时候,该节点的深度乘以交换一次的代价。
通过刚刚的知识,最远距离是到两个端点的距离的最大值,所以在找到直径端点后,分别以端点为根,DFS一遍,比较出最远距离,即价值。
最后再用价值-代价,求出该式子的最大值。
3、代码
#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 2e5 + 10;
int dep[N], c, cost[N], dep2[N],cc;
vector<int>edge[N];
void deep(int u, int father)
{
for(auto son: edge[u])
{
if(son == father)
continue;
cost[son] = cost[u] + 1;
deep(son, u);
}
}
void dfs(int u, int father)
{
for(auto son : edge[u])
{
if(son == father)
continue;
dep[son] = dep[u] + 1;
if(dep[son] > dep[c])
c = son;
dfs(son, u);
}
}
void dfs2(int u, int father)
{
for(auto son : edge[u])
{
if(son == father)
continue;
dep2[son] = dep2[u] + 1;
if(dep2[son] > dep2[cc])
cc = son;
dfs2(son, u);
}
}
void solve()
{
int n, k, m;
cin >> n >> k >> m;
for(int i = 0; i < n - 1; i ++ )
{
int a, b;
cin >> a >> b;
edge[a].push_back(b);
edge[b].push_back(a);
}
cost[1] = 0;
deep(1, -1);
dep[1] = 0;
dfs(1, -1);
dep2[c] = 0;
dfs2(c, -1);
dep[cc] = 0;
dfs(cc, -1);
int maxv = 0;
for(int i = 1; i <= n; i ++ )
maxv = max(max(dep[i], dep2[i]) * k - cost[i] * m, maxv);
cout << maxv << endl;
for(int i = 1; i <= n; i ++)
{
dep[i] = dep2[i] = cost[i] = 0;
edge[i].clear();
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
G1. Magic Triples (Easy Version)
1、问题
给定一个数组,从中挑出三个不同位置的数字,构成一个等比数列,求方案数。
2、分析
G 1 G1 G1是简单版本,所以这道题的数据范围比较小。
首先我们利用一个数组存储数字 x x x的出现次数,记作 c n t [ x ] cnt[x] cnt[x]。
我们先看公比是1的情况,这种情况下,三个数字相等。当出现次数大于2的时候,就会有这种方案。方案数为:
(
c
n
t
[
x
]
)
∗
(
c
n
t
[
x
]
−
1
)
∗
(
c
n
t
[
x
]
−
2
)
(cnt[x])*(cnt[x]-1)*(cnt[x]-2)
(cnt[x])∗(cnt[x]−1)∗(cnt[x]−2)
当公比不是 1 1 1的时候,我们只需要去遍历数组,然后对于任何一个数组元素 a [ i ] a[i] a[i],再去枚举所有可能的公比,然后找到对应的 a [ i ] ∗ b a[i]*b a[i]∗b和 a [ i ] ∗ b 2 a[i]*b^2 a[i]∗b2的出现次数。此时对答案的贡献就是: c n t [ a [ i ] ] ∗ c n t [ a [ i ] ∗ b ] ∗ c n t [ a [ i ] ∗ b 2 ] cnt[a[i]]*cnt[a[i]*b]*cnt[a[i]*b^2] cnt[a[i]]∗cnt[a[i]∗b]∗cnt[a[i]∗b2]
3、代码
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
#define int long long
using namespace std;
const int N = 1e6 + 10;
int cnt[N];
void solve()
{
int n, ans = 0;
cin >> n;
vector<int>a(n);
set<int>nums;
int maxv = -INF;
for(int i = 0; i < n; i ++)
{
cin >> a[i];
nums.insert(a[i]);
cnt[a[i]]++;
maxv = max(a[i], maxv);
}
for(auto x : nums)
if(cnt[x] > 2)
ans += (cnt[x] - 1) * (cnt[x]) * (cnt[x] - 2);
for(auto x : nums)
{
for(int j = 2; j * j <= maxv; j ++)
{
if(x * j * j <= maxv)
ans += (cnt[x] * cnt[x * j] * cnt[x * j * j]);
}
}
for(auto x : nums)
cnt[x] = 0;
cout << ans << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
G2. Magic Triples (Hard Version)
1、问题
困难版本即将数据范围从 1 0 6 10^6 106提升到了 1 0 9 10^9 109。
2、分析
此时我们的
c
n
t
cnt
cnt数组无法用数组来存储,只能使用
m
a
p
map
map。
接下来我们要讨论一下如何求方案。
求方案数必定需要遍历每一个元素,该过程需要花费的时间是 1 e 5 1e5 1e5的,所以留给我们判断的时间只有 1 e 3 1e3 1e3
当公比是1的时候,依然采用: ( c n t [ x ] ) ∗ ( c n t [ x ] − 1 ) ∗ ( c n t [ x ] − 2 ) (cnt[x])*(cnt[x]-1)*(cnt[x]-2) (cnt[x])∗(cnt[x]−1)∗(cnt[x]−2)
当公比不是1的时候,怎么办呢?
刚刚的方案是去枚举三个数当中最小的那个,现在我们则是要去枚举中间大的那个数字,即 x ∗ b x*b x∗b。很明显,如果去枚举中间这个数字的话,公比就必须是这个数的因数,所以我们的公比只需要去枚举这个数的因数。
枚举 a [ i ] a[i] a[i]的因数,我们只需要去枚举1到 a [ i ] \sqrt {a[i]} a[i],即求因数的复杂度是 O ( a [ i ] ) O(\sqrt {a[i]}) O(a[i])的,由于我们刚刚分析出求方案的时间要控制在 1 e 3 1e3 1e3之内,即只有当 a [ i ] a[i] a[i]小于 1 0 6 10^6 106的时候,我们才能用这种算法。
那么当 a [ i ] ≥ 1 0 6 a[i]\geq10^6 a[i]≥106的时候,我们可以采用刚刚的方法,即枚举 b b b。因为 a [ i ] < 1 e 9 a[i]<1e9 a[i]<1e9,所以我们的 b b b只需要从 1 1 1枚举到 1 e 3 1e3 1e3。恰好符合我们的时间要求。
上述这种按照数据大小分类的算法,叫做分块算法。
3、代码
#include<bits/stdc++.h>
#define int long long
#define INF 0x3f3f3f3f
using namespace std;
const int N = 2e5 + 10;
int a[N];
void solve()
{
int n;
cin >> n;
int maxv = -INF;
map<int,int>cnt;
for(int i = 0; i < n; i ++)
{
cin >> a[i];
maxv = max(maxv, a[i]);
cnt[a[i]] ++;
}
int ans = 0;
for(auto x : cnt)
if(x.second > 2)
ans += (cnt[x.first]) * (cnt[x.first] - 1) * (cnt[x.first] - 2);
for(auto x: cnt)
{
int num = x.first;
int val = x.second;
if(num > 1e6)
{
for(int b = 2; b * num <= maxv; b ++)
if(num % b == 0 && cnt.find(num / b) != cnt.end() && cnt.find(num * b) != cnt.end())
ans += (val) * cnt[num / b] * cnt[num * b];
}
else
{
for(int b = 1; b * b <= num; b ++)
if(num % b == 0)
{
if(b != 1 && cnt.count(num / b) && cnt.count(num * b))
ans += val * cnt[num / b] * cnt[num * b];
int nex = num / b;
if( nex != 1 && nex != b && cnt.count(num / nex) && cnt.count(num * nex))
ans += val * cnt[num / nex] * cnt[num * nex];
}
}
}
cout << ans << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while(t--)
solve();
}