- 博主简介:想进大厂的打工人
- 博主主页:@xyk:
- 所属专栏: JavaEE初阶
目录
文章目录
一、选择题1
二、[编程题]养兔子
三、[编程题]求正数数组的最小不可组成和
一、选择题1
reflection是如何工作的__牛客网 (nowcoder.com)
考虑下面这个简单的例子,让我们看看reflection是如何工作的。
import java.lang.reflect.*;
public class DumpMethods{
public static void main(String[] args) {
try {
Class c=Class.forName(args[0]);
Method m[]=c.getDeclaredMethods();
for (int i = 0; i < m.length; i++) {
System.out.println(m[i].toString());
}
} catch (Throwable e) {
System.err.println(e);
}
}
}其中"c.getDeclaredMethods"的作用是:

public Method[] getDeclaredMethods()返回类或接口声明的所有方法,包括public, protected, default (package) 访问和private方法的Method对象,但不包括继承的方法。当然也包括它所实现接口的方法。
public Method[] getMethods()返回类的所有public方法,包括其继承类的公用方法,当然也包括它所实现接口的方法。
所以答案选D~~~
二、[编程题]养兔子
养兔子__牛客网 (nowcoder.com)
一只成熟的兔子每天能产下一胎兔子。每只小兔子的成熟期是一天。 某人领养了一只小兔子,请问第N天以后,他将会得到多少只兔子。
对于这样的题目主要是抓住递推式的关系。
我对于F(n)=F(n-1)+1*F(n-2)的公式理解是这样的。F(n-1)代表昨天的兔子总量。
F(n-2)代表前天的兔子总量,刚好只有前天的兔子具有生产能力。
//就是斐波那契数列
import java.util.Scanner;
public class Main {
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
while(sc.hasNext()){
int n = sc.nextInt();
long[] arr = new long[91];
arr[1] = 1;
arr[2] = 2;
for(int i = 3;i < arr.length;i++){
arr[i] = arr[i-1] + arr[i-2];
}
System.out.println(arr[n]);
}
}
}
所以如果题目改成一只成熟的兔子能够生产2只,那么通项公式为F(n)=F(n-1)+2*F(n-2)
方法二:
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
while(sc.hasNext()){
int n = sc.nextInt();
long f0 = 1;
long f1 = 1;
long f2 = 1;
for(int i = 2;i <= n;i++){
f2 = f1 +f0;
f0 = f1;
f1 = f2;
}
System.out.println(f2);
}
}三、[编程题]求正数数组的最小不可组成和
链接:求正数数组的最小不可组成和_百度笔试题_牛客网
来源:牛客网
给定一个全是正数的数组arr,定义一下arr的最小不可组成和的概念:
1,arr的所有非空子集中,把每个子集内的所有元素加起来会出现很多的值,其中最小的记为min,最大的记为max;
2,在区间[min,max]上,如果有一些正数不可以被arr某一个子集相加得到,那么这些正数中最小的那个,就是arr的最小不可组成和;
3,在区间[min,max]上,如果所有的数都可以被arr的某一个子集相加得到,那么max+1是arr的最小不可组成和;
举例: arr = {3,2,5} arr的min为2,max为10,在区间[2,10]上,4是不能被任何一个子集相加得到的值中最小的,所以4是arr的最小不可组成和; arr = {3,2,4} arr的min为2,max为9,在区间[2,9]上,8是不能被任何一个子集相加得到的值中最小的,所以8是arr的最小不可组成和; arr = {3,1,2} arr的min为1,max为6,在区间[2,6]上,任何数都可以被某一个子集相加得到,所以7是arr的最小不可组成和;
请写函数返回arr的最小不可组成和。
看了题之后, 是不是没有思路??
我看题之后,首先想到了把所有元素组合的方式加起来,填入一个集合中,然后一个一个进行比对,如果从小到大没有的数,就返回~~两种情况!
1.[min,max] 有正数不能被子集相加得到! 返回该数
2.[min,max] 所以正数都能被子集相加得到 返回 max+1
回溯法:
import java.util.*;
public class Solution {
/**
* 正数数组中的最小不可组成和
* 输入:正数数组arr
* 返回:正数数组中的最小不可组成和
*/
public void getNumber(int[] arr,ArrayList<Integer> result,int pos,int sum){
if(pos==arr.length){
return;
}
for(int i = pos;i<arr.length;i++){
sum += arr[i];
result.add(sum);
getNumber(arr,result,i+1,sum);
sum -= arr[i];
}
}
public int getFirstUnFormedNum(int[] arr) {
//2种情况: 1.[min,max] 有正数不能被子集相加得到! 返回该 数
// 2.[min,max] 所以正数都能被子集相加得到 返回 max+1
Arrays.sort(arr);
int min = arr[0];
int max = arr[0];
ArrayList<Integer> result = new ArrayList<>();
getNumber(arr,result,0,0);
for(int i = 1;i<arr.length;i++){
max += arr[i];
}
for(int i = min+1;i<max;i++){
if(!result.contains(i)){
return i;
}
}
return max+1;
}
}方法二:想象为背包问题
1、我们先来看一个背包问题:
思路借鉴牛客大佬
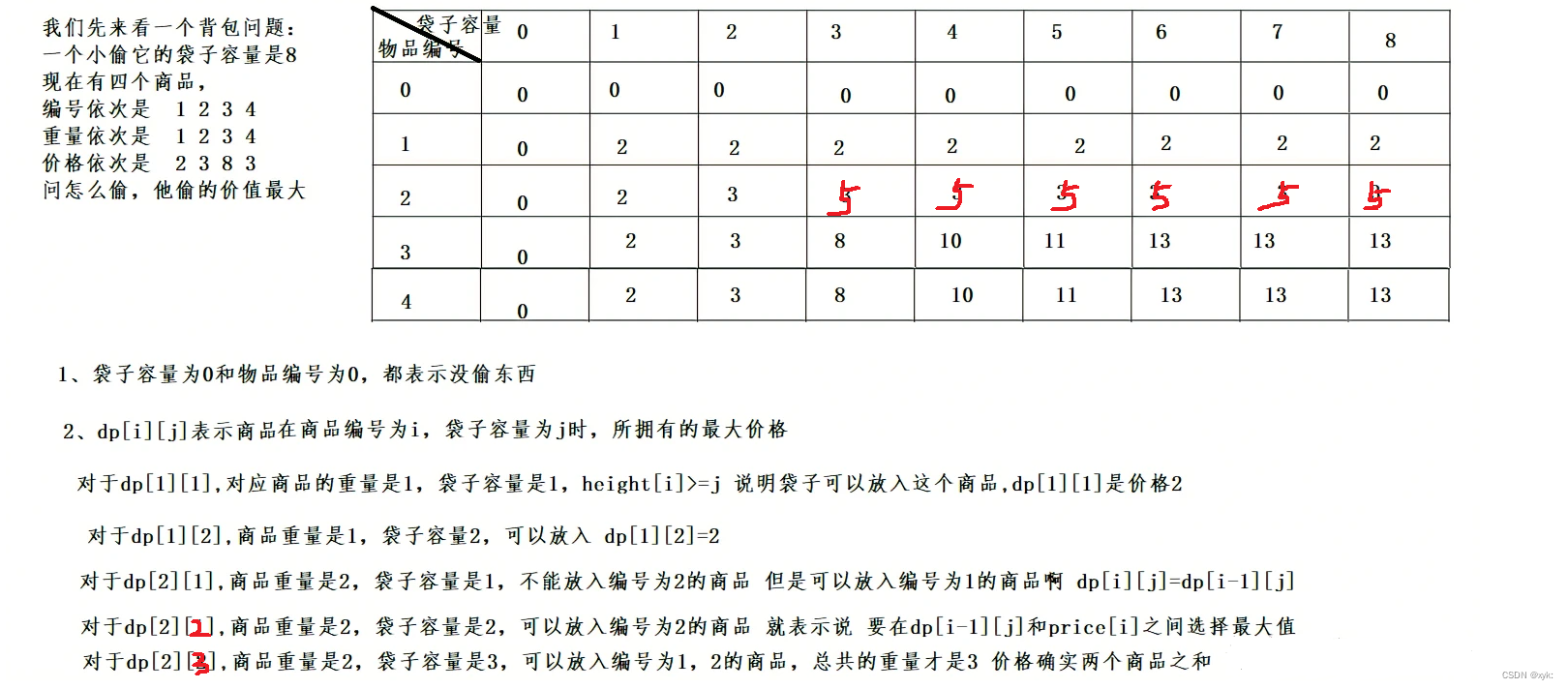

此时,模拟背包问题代码:
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();//输入商品个数
int Max_room = scanner.nextInt();//输入袋子容量
int[] weight = new int[n];
int[] price = new int[n];
int i = 0;
while (i < n){
weight[i++] = scanner.nextInt();
}
i = 0;
while (i < n){
price[i++] = scanner.nextInt();
}
int[][] dp = new int[n + 1][Max_room + 1];
for (i = 1; i <= n; i++) {
for (int j = 1; j <= Max_room; j++) {
if (weight[i - 1] > j) {//袋子的容量不够
dp[i][j] = dp[i - 1][j];
} else {//袋子容量足够
dp[i][j] = Math.max(dp[i - 1][j], price[i - 1] + dp[i - 1][j - weight[i - 1]]);
}
}
}
System.out.println(dp[n][Max_room]);
}这道题,可以看作是背包问题的变形 背包容量的范围在【min,max】,arr数组相当于每个物品的重量
如果背包容量和所承载的物品重量不相等,就是所求
可以转换的原因是:背包容量[min,max]是数组的子集之和的范围
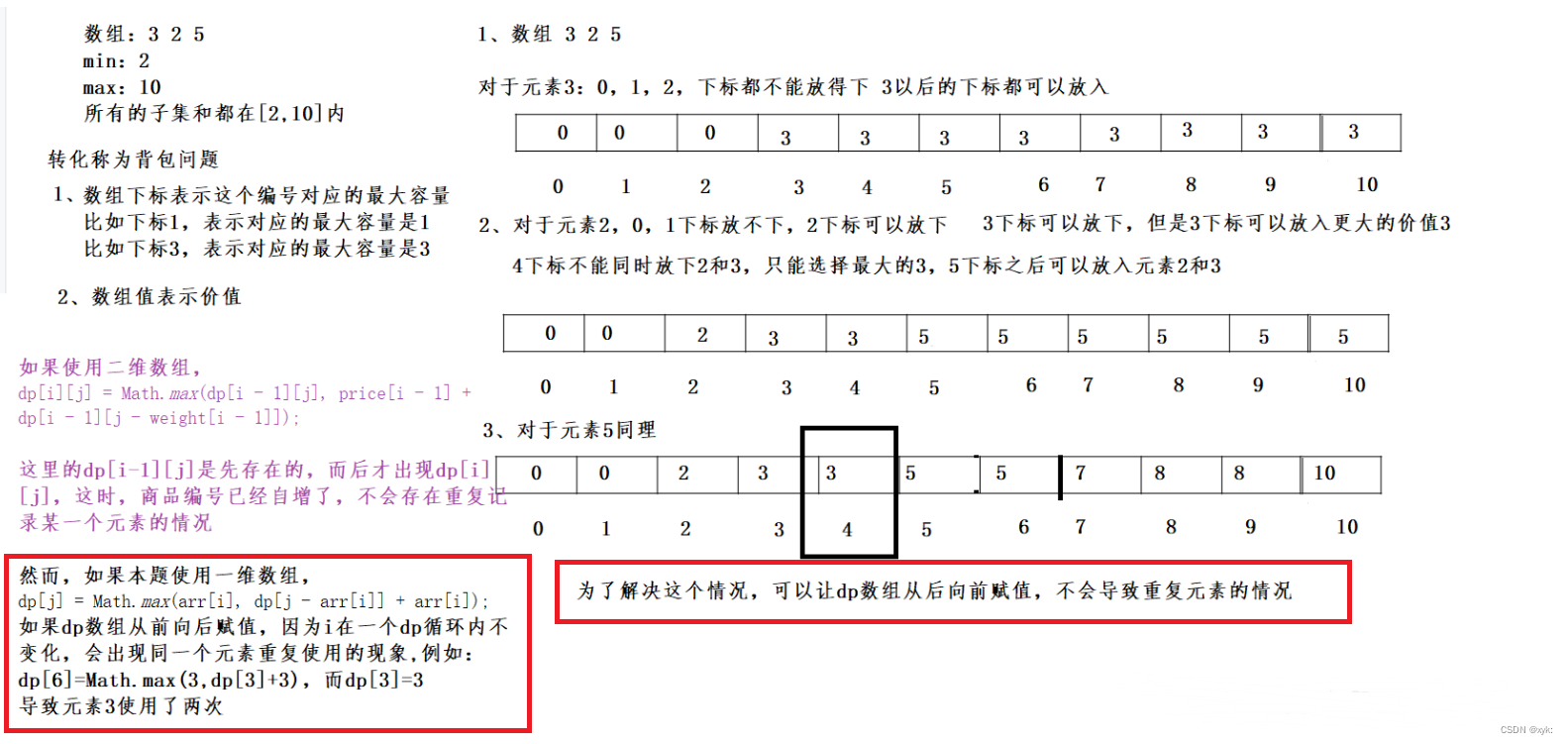
public static int getFirstUnFormedNum(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
if (arr.length == 1) {//只有一个元素 ,在区间[min,max]上,如果所有的数都可以被arr的某一个子集相加得到,那么max+1是arr的最小不可组成和;
return arr[0] + 1;
}
int min = arr[0];
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
max += arr[i];
min = Math.min(arr[i], min);
}
int[] dp = new int[max + 1];
for (int i = 0; i <arr.length ; i++) {
for (int j = max; j >= arr[i]; j--) {
//dp数组从后向前赋值
dp[j] = Math.max(dp[j], dp[j - arr[i]] + arr[i]);
}
}
for (int i = min; i < max; i++) {
if (dp[i] != i)
return i;
}
return max + 1;
}