二叉树

1 二叉树的种类

1.1 满二叉树

节点数量为 2^k - 1 (k是树的深度，底层的叶子节点都是满的）
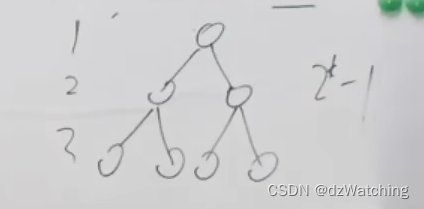
在这里插入图片描述

1.2 完全二叉树

完全二叉树是指除了下面一层外，其余层的节点都是满的；
且最下面一层的叶子节点是从左到右连续的。
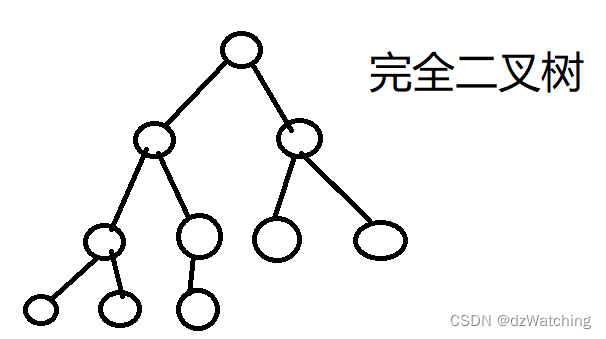
在这里插入图片描述
下面这个树的底层叶子节点就不是从左到右连续的，所以不是完全二叉树

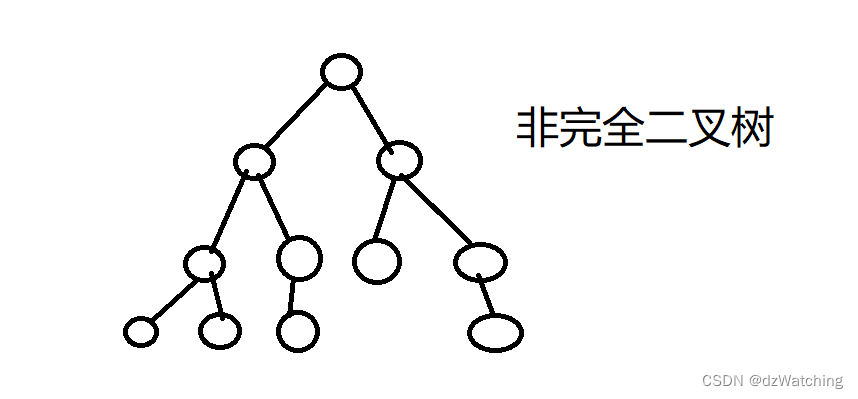
满二叉树一定式完全二叉树，完全二叉树不一定是满二叉树。

1.3 二叉搜索树

二叉搜索树对节点的布局是没有要求的；
二叉搜索树对节点的排序有要求：左子树的数据 < 中间节点的数据
右子树的数据 > 中间节点的数据

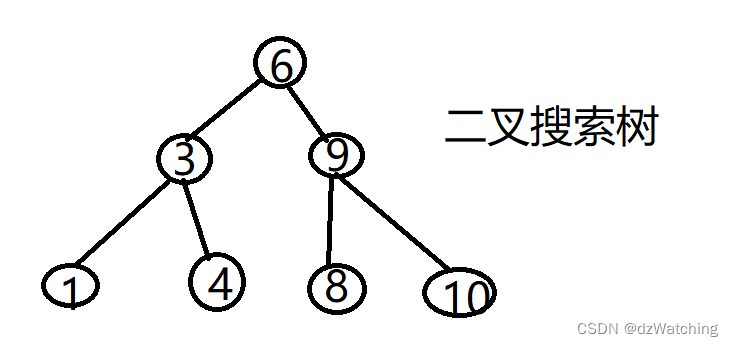
在这里插入图片描述
下图也是一个二叉搜索树，因为二叉搜索树对节点布局没有要求

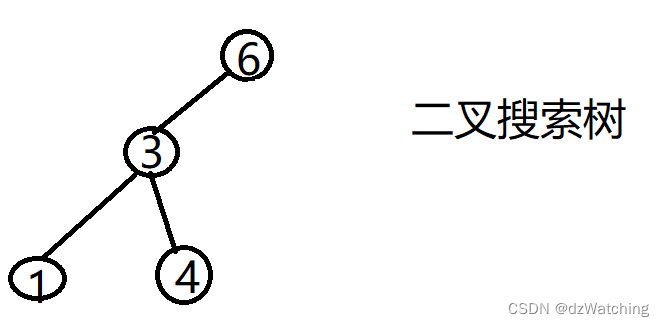
1.4 平衡二叉搜索树

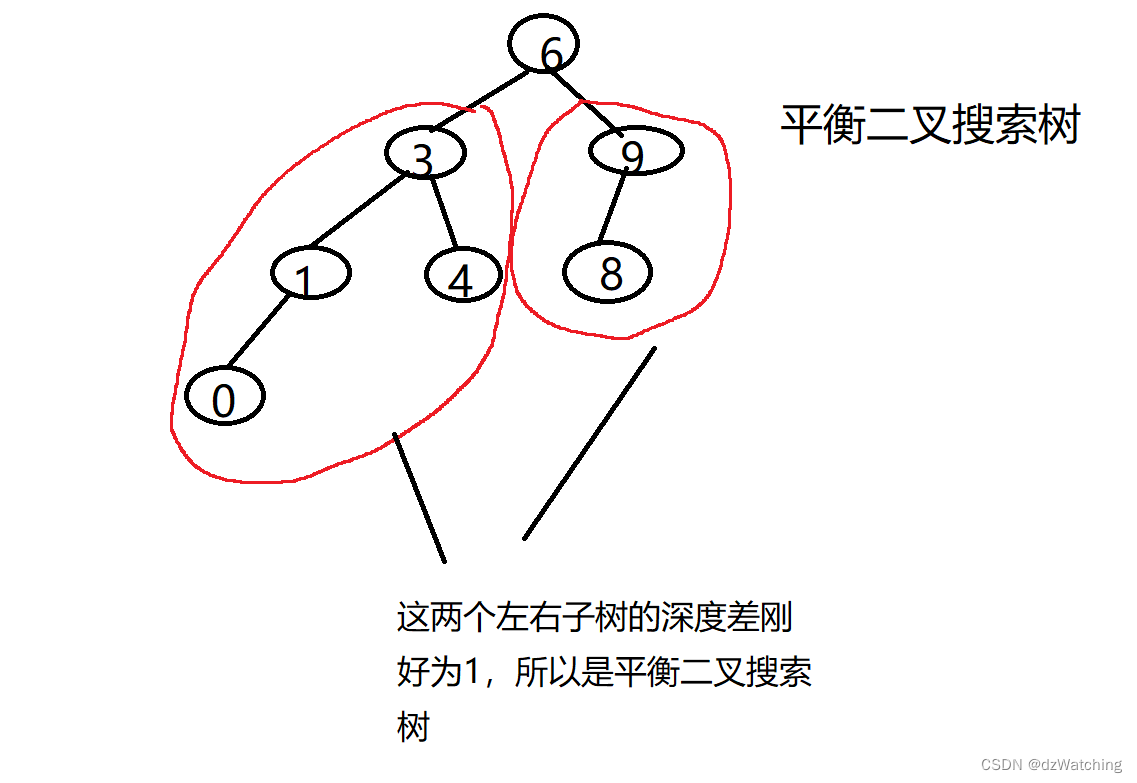
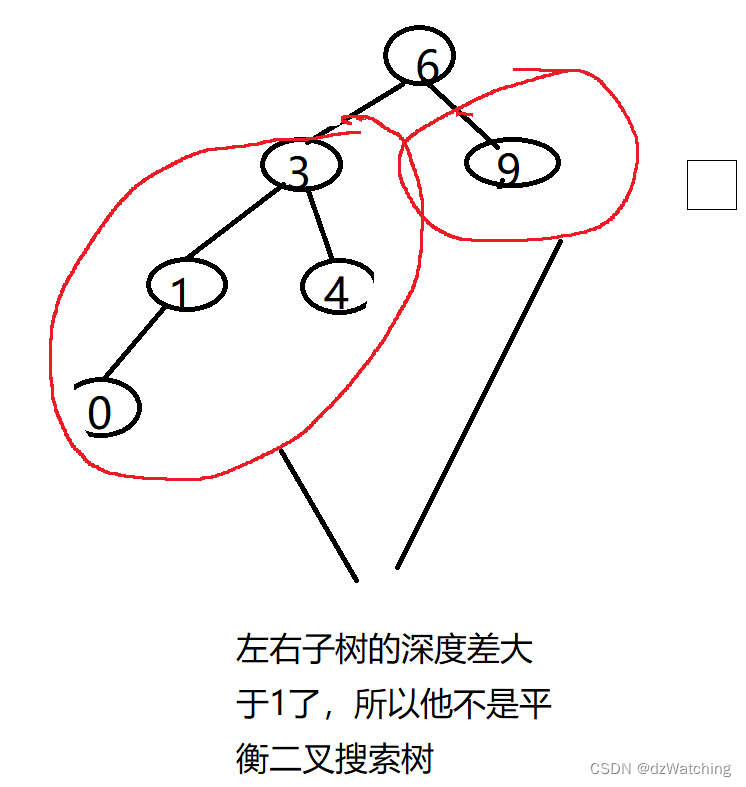
平衡二叉搜索树和二叉搜索树一样也需要排序；
不同的是平衡二叉搜索树对布局有要求：平衡二叉搜索树的左子树和右子树的深度差不能大于1
在这里插入图片描述

2 二叉树的存储方式

2.1 链式存储

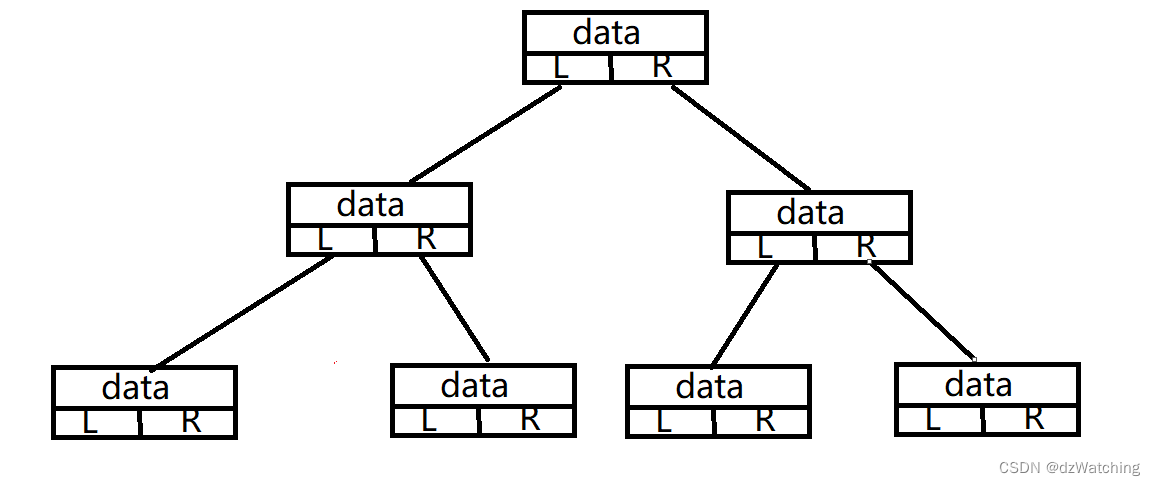
链式存储就是指使用链表的方式存储：
每个节点有三个域：①数据域②左指针③右指针
在这里插入图片描述

2.2 顺序存储

顺序存储是指使用数组存储：
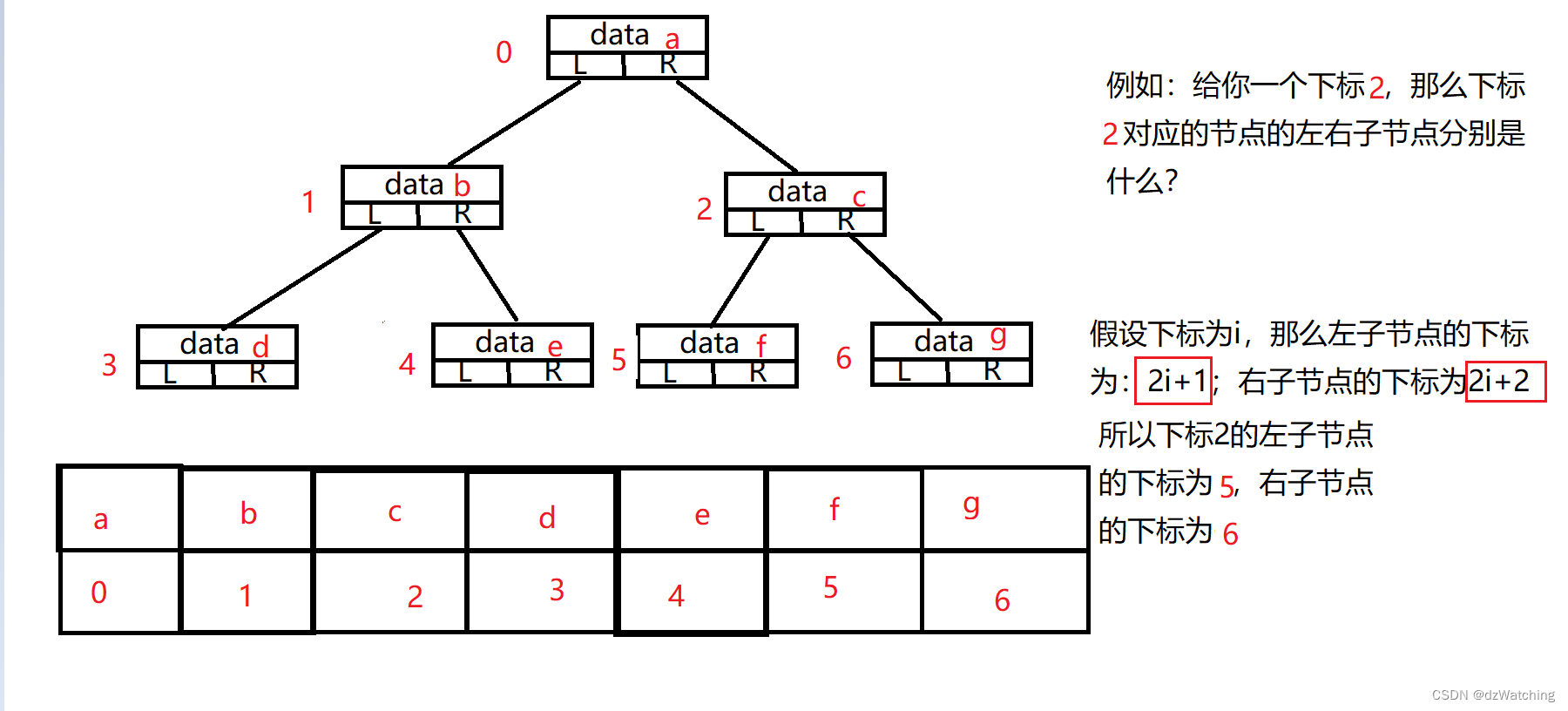
在这里插入图片描述

3 遍历方式

3.1 深度优先遍历

前中后序遍历都属于深度优先遍历，可以使用递归遍历，也可以使用迭代遍历。
如果使用递归遍历，需要牢记三个步骤：
①确定递归函数的参数与返回值
②确定终止条件
③确定单层递归的逻辑

package leetcode.A_4_二叉树的前序遍历;

import java.util.ArrayList;
import java.util.List;

/**
 * @author Watching
 * * @date 2023/4/30
 * * Describe:
 * 二叉树的前序遍历
 */


public class Solution {
    public static void main(String[] args) {
        TreeNode treeNode1 = new TreeNode(1);
        TreeNode treeNode2 = new TreeNode(2);
        TreeNode treeNode3 = new TreeNode(3);
        treeNode1.right = treeNode2;
        treeNode2.left = treeNode3;
        System.out.println(preorderTraversal(treeNode1));
    }


    public static List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        //确定终止条件
        func(list, root);//将具体代码抽象出去
        return list;
    }

    public static void func(List<Integer> list, TreeNode root) {
        if (root != null) {
            list.add(root.val); // 通过改变这行代码的位置就可以实现前序，中序，后序遍历
            func(list, root.left);
            func(list, root.right);
        }
    }
}

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}