第一次力扣,等大二寒暑假,有时间再来系统刷题
目录
🌼前言
🌼一,6341.保龄球游戏的获胜者
🌼二,6342.找出叠涂元素
🌳第一次 -- 超时
🌳第二次 -- AC
🌼前言
一共4题,1道easy,2道midium,1道hard,比赛时,不懂面向对象的return和vector越界的问题
浪费了很久,一个半小时,最后只AC了第1题
下面是1,2题的记录
🌼一,6341.保龄球游戏的获胜者
6341. 保龄球游戏的获胜者 - 力扣(LeetCode)



本题有个小坑,“第i轮价值”的描述中,“前2轮”意思是当前往前2轮,而不是初始2轮
导致大多数人,错了2次才做对
耗时17分钟
AC 代码
class Solution {
public:
int isWinner(vector<int>& player1, vector<int>& player2) {
int sum1 = 0, sum2 = 0, n = player1.size();
for(int i = 0; i < n; ++i) {
sum1 += player1[i];
sum2 += player2[i];
if(i == 1 && player1[0] == 10)
sum1 += player1[i];
if(i == 1 && player2[0] == 10)
sum2 += player2[i];
if(i >= 2 && (player1[i - 1] == 10 || player1[i - 2] == 10))
sum1 += player1[i];
if(i >= 2 && (player2[i - 1] == 10 || player2[i - 2] == 10))
sum2 += player2[i];
}
if(sum1 > sum2) return 1;
else if(sum1 == sum2) return 0;
else return 2;
}
};🌼二,6342.找出叠涂元素
6342. 找出叠涂元素 - 力扣(LeetCode)
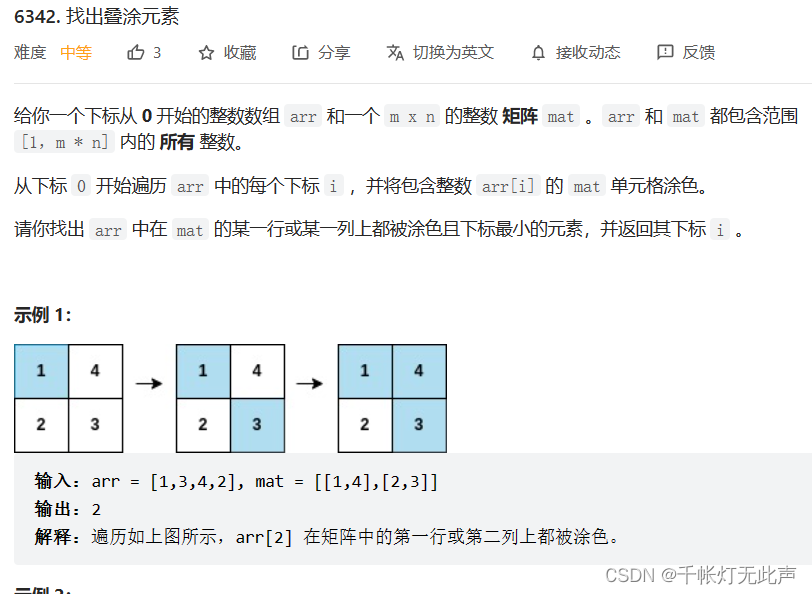

耗时一个半小时,半小时不了解vector和return,半小时暴力做法,最后还是TLE了
本题在return挣扎了很久
1,非void型函数,所有路径都要有return ...,确定的返回值
2,return 3;这样,它才会输出3,而不是cout<<3;
3,本题暴力O(m^2 * n^2) = 10^10,会TLE(time limit exceeded),需要用巧妙方法O(mn)
🌳第一次 -- 超时
class Solution {
public:
int row_color[100010], col_color[100010];
int firstCompleteIndex(vector<int>& arr, vector<vector<int>>& mat) {
int m = mat.size(), n = mat[0].size();
//vector<int>row_color = {m, 0}; //标记该行已被涂色
//vector<int>col_color = {n, 0}; //标记该列已被涂色
//得到每 行/列 涂色数
for(int i = 0; i < m * n; ++i) {
int num = arr[i]; //当前数字
for(int j = 0; j < m; ++j) {
for(int k = 0; k < n; ++k) {
if(mat[j][k] == num) {
row_color[j] += 1; //记录第j行被涂色总数
col_color[k] += 1;
}
}
}
//遍历行
for(int j = 0; j < m; ++j) {
if(row_color[j] == n)
return i;
}
//遍历列
for(int k = 0; k < n; ++k) {
if(col_color[k] == m)
return i;
}
}
return m * n - 1;
}
};
下面介绍下巧妙方法
在第一次代码的基础上(使用row_color[]和col_color[]数组保存某一行/列已经上色的数量)
增加R[], C[]数组,
R[mat[i][j]] = i; 表示元素mat[i][j]在第i行
R[mat[i][j]] = j; 表示元素mat[i][j]在第j列
比如R[7] = 2; 表示7这个数字在第3行(下标从0开始)
这样就可以边统计,当前某行/列的上色数,边判断是否满足条件,O(mn)解决问题
其实就是预处理,先准备好要用的
🌳第二次 -- AC
class Solution {
public:
int firstCompleteIndex(vector<int>& arr, vector<vector<int>>& mat) {
int m = mat.size(), n = mat[0].size();
int R[m*n+1], C[m*n+1]; //单个元素最大达m*n
//预处理
for(int i = 0; i < m; ++i)
for(int j = 0; j < n; ++j) {
R[mat[i][j]] = i; //元素mat[i][j]在第i行
C[mat[i][j]] = j; //元素mat[i][j]在第j列
}
int row_color[m + 1], col_color[n + 1]; //记录某一 行/列 上色的总数
//初始化为0
memset(row_color, 0, sizeof(row_color));
memset(col_color, 0, sizeof(col_color));
//复杂度O(m*n)
for(int i = 0; i < m * n; ++i) {
int r = R[arr[i]], c = C[arr[i]]; //arr[i]所属的 行/列
row_color[r]++; //上色数+1
col_color[c]++; //上色数+1
if(row_color[r] == n || col_color[c] == m)
return i;
}
return -1; //确保所有路径下都有返回值
}
};