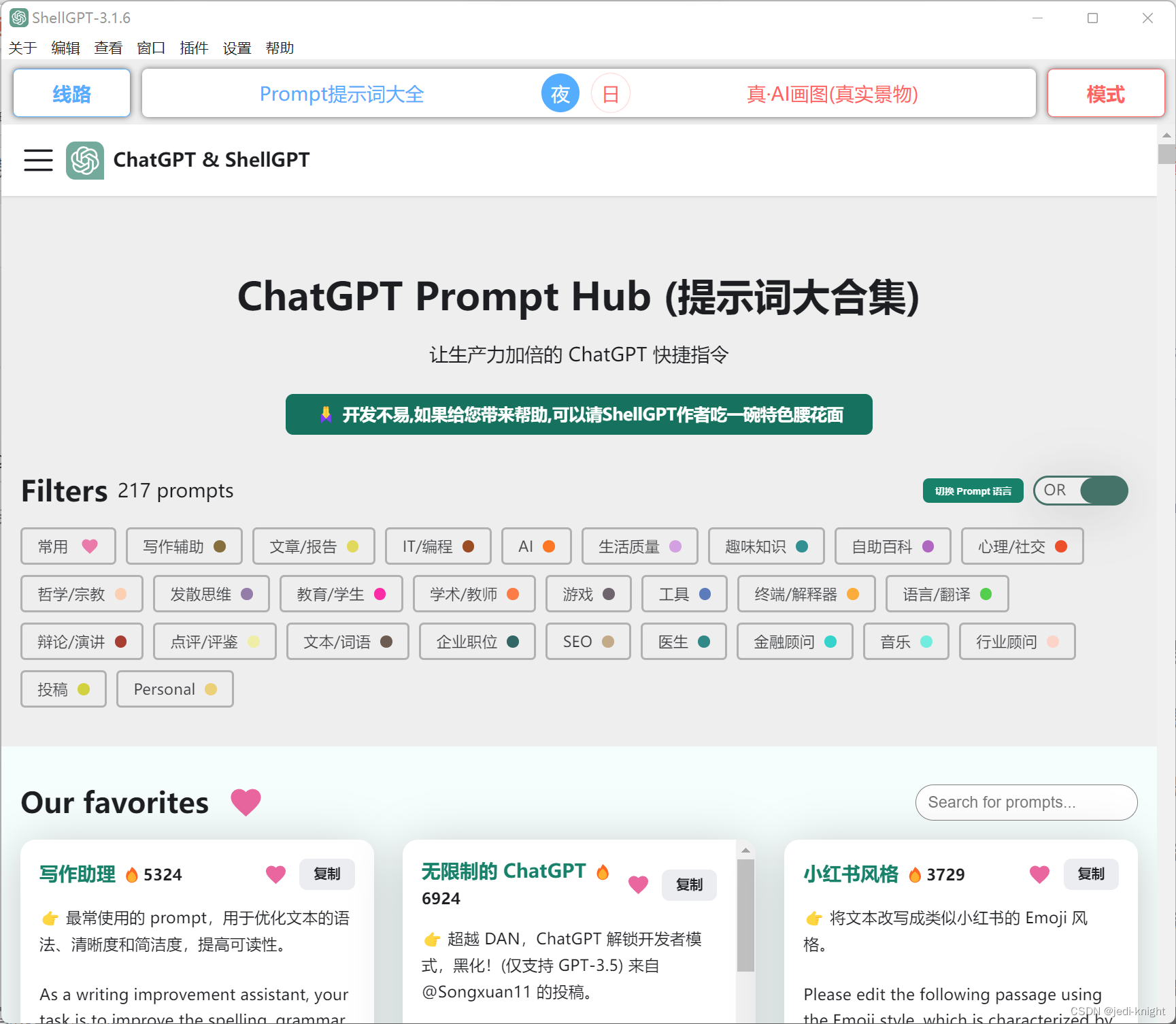
1 ShellGPT

这是一款出色的客户端，无需APIkey和科学上网即可访问chatGPT3.5以及绘画AI。项目的github地址如下：https://github.com/akl7777777/free-chatgpt-client-pub/，可在主页下载windows、linux和macOS的安装包，安装后即可使用

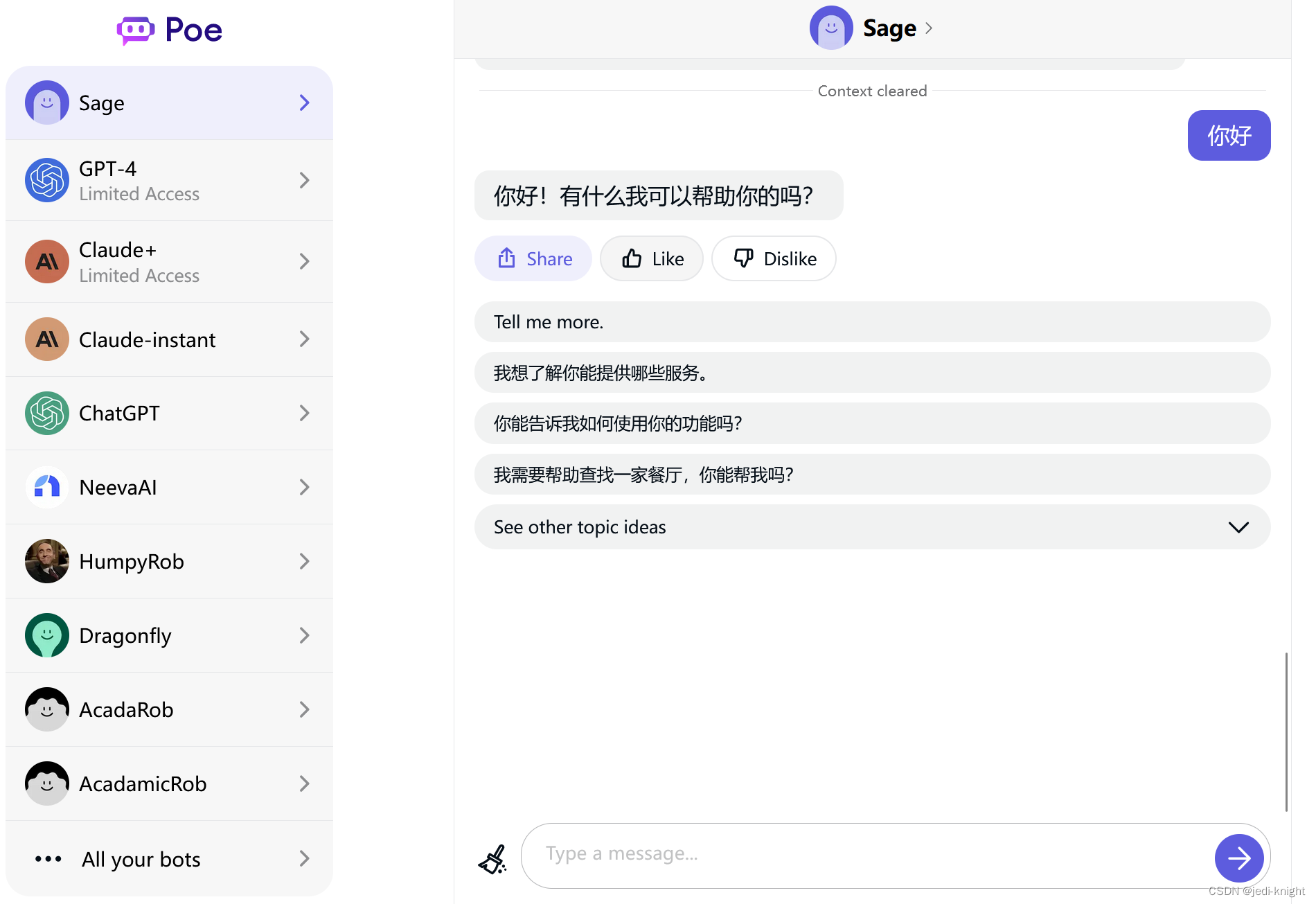
2 Poe

Poe集成了许多聊天机器人，包括GPT、Sage、Claude等。其中Sage机器人对中文的支持很好。其网址为https://poe.com，需要科学上网。

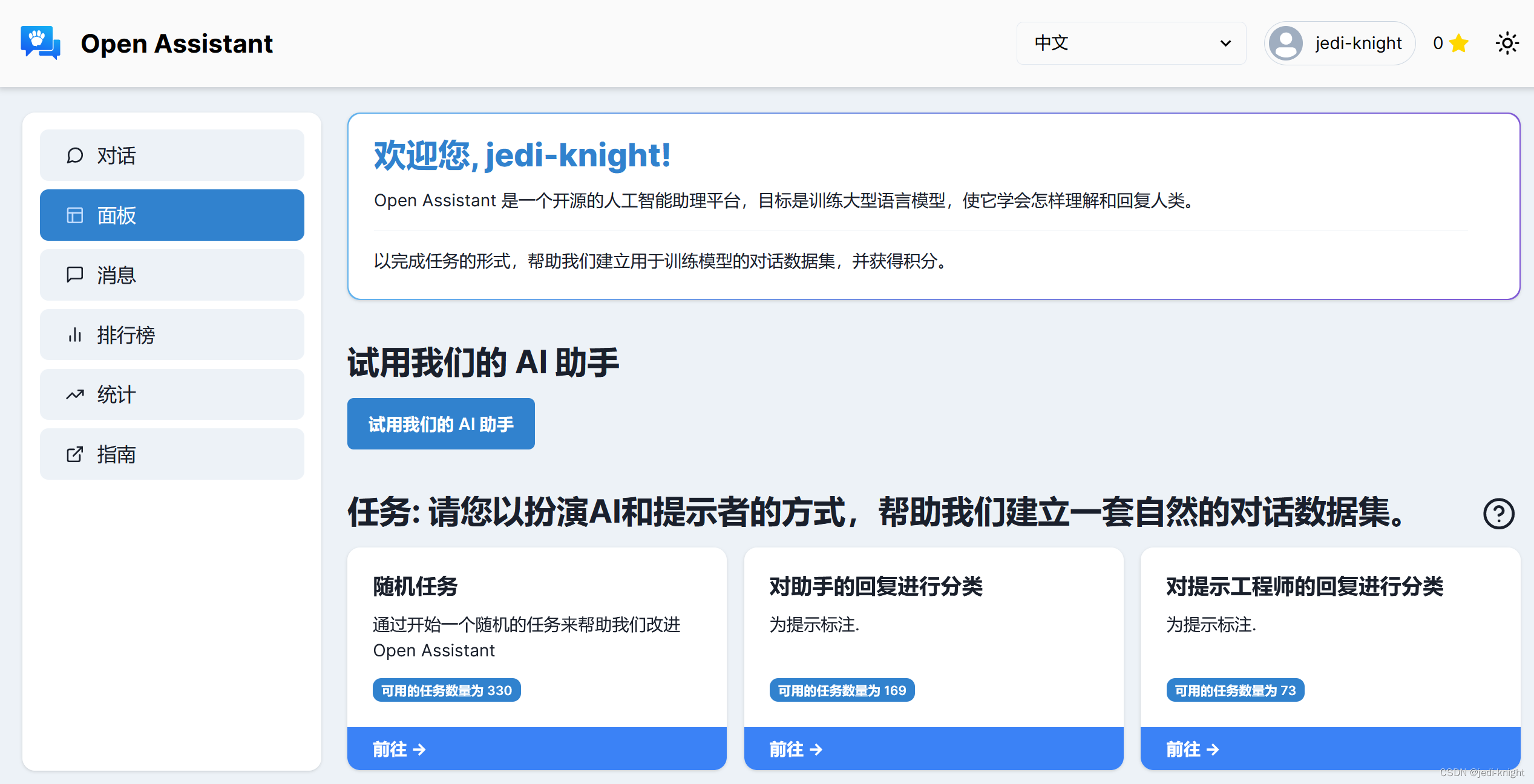
3 OpenAssistant

Open Assistant 是一个开源的人工智能助理平台，有300万亿参数，是目前开源大语言模型中最强大的，但是对中文支持很差。其网址为https://open-assistant.io/zh/dashboard，无需科学上网，可注册使用。

3 HuggingChat

HuggingChat与OpenAssistant使用的模型相同，也是目前开源大语言模型中最强大的，但是对中文支持很差。其网址为https://huggingface.co/chat/，无需科学上网和注册，开箱即用。