快速傅里叶变换FFT学习笔记

news2024/10/6 20:27:26

点值表示法

我们正常表示一个多项式的方式，形如 A ( x ) = a 0 + a 1 x + a 2 x 2 + . . . + a n x n A(x)=a_0+a_1x+a_2x^2+...+a_nx^n A(x)=a0​+a1​x+a2​x2+...+an​xn，这是正常人容易看懂的，但是，我们还有一种表示法。

我们知道， n + 1 n+1 n+1个点可以表示出一个 n n n 次的多项式。

于是，我们任意地取 n + 1 n+1 n+1 个不同的值，表示 x x x ，求出的值与 x x x 对应，形成 n + 1 n+1 n+1个点，这就可以表示。

复数

一种表示坐标的方法，对于坐标 ( x , y ) (x,y) (x,y),可写作 x + i y x+iy x+iy，其中 x x x为实部， y y y为虚部。

C++中有复数的模板，complex，可以直接作为变量类型使用。

运算规则，自然不用多说了，也就是直接拿式子算即可。

如果你不会，可以看看百度百科。

我们将点至原点的距离称为模长，将其与原点相连之后与 x x x 轴形成的一个夹角称为辐角，不过呢，对于第三第四象限的点，自然要加上一个 180 ° 180° 180°了。

我的表述自然不够专业，希望可以表述出这个意思吧。

复数的乘法可以理解为，模长相乘，辐角相加。

Tips：

此部分的证明来自 cjx 犇犇。

为啥是这样呢？证明如下:

( a + b i ) ( c + d i ) = a c − b d + i ( b c + a d ) (a+bi)(c+di)=ac-bd+i(bc+ad) (a+bi)(c+di)=ac−bd+i(bc+ad)

那么这个点就是 ( a c − b d , b c + a d ) (ac-bd,bc+ad) (ac−bd,bc+ad)，其模长:

( a c − b d ) 2 + ( b c + a d ) 2 = ( a c ) 2 − 2 a b c d + ( b d ) 2 + ( b c ) 2 + 2 a b c d + ( a d ) 2 = ( a c ) 2 + ( b d ) 2 + ( b c ) 2 + ( a d ) 2 = ( a 2 + b 2 ) ( c 2 + d 2 ) \sqrt{(ac-bd)^2+(bc+ad)^2}\\ =\sqrt{(ac)^2-2abcd+(bd)^2+(bc)^2+2abcd+(ad)^2}\\ =\sqrt{(ac)^2+(bd)^2+(bc)^2+(ad)^2}\\ =\sqrt{(a^2+b^2)(c^2+d^2)}\\ (ac−bd)2+(bc+ad)2 ​=(ac)2−2abcd+(bd)2+(bc)2+2abcd+(ad)2 ​=(ac)2+(bd)2+(bc)2+(ad)2 ​=(a2+b2)(c2+d2) ​

那么我们应该可以看出来这个模长相乘了。

接下来是辐角相加，我们设原来两个辐角为 θ 1 , θ 2 \theta_1,\theta_2 θ1​,θ2​，而模长为 t 1 , t 2 t_1,t_2 t1​,t2​。

cos ⁡ ( θ 1 + θ 2 ) = cos ⁡ ( θ 1 ) cos ⁡ ( θ 2 ) − sin ⁡ ( θ 1 ) sin ⁡ ( θ 2 ) = a t 1 × c t 2 − b t 1 × d t 2 = a c − b d t 1 t 2 \cos(\theta_1+\theta_2)=\cos(\theta_1)\cos(\theta_2)-\sin(\theta_1)\sin(\theta_2)\\ =\frac {a}{t_1}\times\frac {c}{t_2}-\frac {b}{t_1}\times\frac {d}{t_2}\\ =\frac {ac-bd}{t_1t_2} cos(θ1​+θ2​)=cos(θ1​)cos(θ2​)−sin(θ1​)sin(θ2​)=t1​a​×t2​c​−t1​b​×t2​d​=t1​t2​ac−bd​

我们知道分母是乘积的模长，分子是横坐标，所以这个式子恰好就是乘积辐角对应的 cos ⁡ \cos cos 值。

那么显然，辐角的值就是 θ 1 + θ 2 \theta_1+\theta_2 θ1​+θ2​了。

把圆均分

img

如图是坐标轴上一个以原点为圆心的半径为 1 1 1 的圆。

我们定义 ω n k \omega_n^k ωnk​表示从 ( 1 , 0 ) (1,0) (1,0)开始，把圆均分为 n n n份的第 k k k个点的复数，其中 ( 1 , 0 ) (1,0) (1,0)为 ω n 0 \omega_n^0 ωn0​。

那么，不难发现， ω n k \omega_n^k ωnk​表示的点为 ( cos ⁡ ( 2 π k n ) , sin ⁡ ( 2 π n k ) ) (\cos(2\pi\frac k n),\sin(2\pi\frac n k)) (cos(2πnk​),sin(2πkn​))。

这是为什么呢？我们考虑它的辐角，由于其平分了一整个圆，所以其辐角为 360 k n ° 360\frac k n° 360nk​°，转换为弧度后则为 2 π k n 2\pi\frac k n 2πnk​，且模长为 1 1 1，利用三角函数易得其坐标了。

简单推推式子不难发现 ( ω n 1 ) k = ω n k (\omega_n^1)^k=\omega_n^k (ωn1​)k=ωnk​，这是利用了模长相乘，辐角相加，因为模长是 1 1 1 ,怎么乘都是 1 1 1，于是辐角不断叠加，从定义上看是这样的。

  • 性质1： ω d n d k = ω n k \omega _{dn}^{dk}=\omega_n^k ωdndk​=ωnk​，根据定义可证。
  • 性质2： ω n k + n 2 = − ω n k \omega _{n}^{k+\frac n 2}=-\omega_n^k ωnk+2n​​=−ωnk​，两点对称。

这个东西有什么用呢？

离散傅里叶变换

离散傅里叶变换(Discrete Fourier Transform，简称DFT)的思想是利用 ω n k \omega_n^k ωnk​将一个多项式转为点值表示法。

对于一个多项式 A ( x ) = a 0 + a 1 x + a 2 x 2 + . . . + a n − 1 x n − 1 A(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1} A(x)=a0​+a1​x+a2​x2+...+an−1​xn−1,我们按照前文所云，将所有的 ω n k \omega_n^k ωnk​作为 x x x 代入。

于是我们得到了 n − 1 n-1 n−1 个点，使用复数形式表示，成为一个数组 ( y 0 , y 1 , y 2 , . . . , y n − 1 ) (y_0,y_1,y_2,...,y_{n-1}) (y0​,y1​,y2​,...,yn−1​)的。

这被称为 A ( x ) A(x) A(x) 的傅里叶变换。

傅里叶逆变换

我们再将其作为一个多项式 B ( x ) = y 0 + y 1 x + . . . . + y n − 1 x n − 1 B(x)=y_0+y_1x+....+y_{n-1}x^{n-1} B(x)=y0​+y1​x+....+yn−1​xn−1。

对于这个多项式 B ( x ) B(x) B(x)，代入所有的 ω n − k \omega_n^{-k} ωn−k​，也就是 ω n k \omega_n^k ωnk​的倒数，得到 ( z 0 , z 1 , z 2 , . . . , z n − 1 ) (z_0,z_1,z_2,...,z_{n-1}) (z0​,z1​,z2​,...,zn−1​)。

易得：

z k = ∑ i = 0 n − 1 y i ( ω n − k ) i = ∑ i = 0 n − 1 ( ∑ j = 0 n − 1 a j ( ω n i ) j ) ( ω n − k ) i = ∑ j = 0 n − 1 a j ( ω n i ) j ∑ i = 0 n − 1 ( ω n − k ) i = ∑ j = 0 n − 1 a j ( ω n j ) i ∑ i = 0 n − 1 ( ω n − k ) i = ∑ j = 0 n − 1 a j ∑ i = 0 n − 1 ( ω n j − k ) i z_k=\sum_{i=0}^{n-1}y_i(\omega_n^{-k})^i \\ =\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j(\omega_n^i)^j)(\omega_n^{-k})^i\\ =\sum_{j=0}^{n-1}a_j(\omega_n^i)^j\sum_{i=0}^{n-1}(\omega_n^{-k})^i\\ =\sum_{j=0}^{n-1}a_j(\omega_n^j)^i\sum_{i=0}^{n-1}(\omega_n^{-k})^i\\ =\sum_{j=0}^{n-1}a_j\sum_{i=0}^{n-1}(\omega_n^{j-k})^i\\ zk​=i=0∑n−1​yi​(ωn−k​)i=i=0∑n−1​(j=0∑n−1​aj​(ωni​)j)(ωn−k​)i=j=0∑n−1​aj​(ωni​)ji=0∑n−1​(ωn−k​)i=j=0∑n−1​aj​(ωnj​)ii=0∑n−1​(ωn−k​)i=j=0∑n−1​aj​i=0∑n−1​(ωnj−k​)i

关于后面那个等比数列，若 j = k j=k j=k，可得 1 1 1，否则用等比数列式子可知为 0 0 0。

因此：

z k = n a k a k = z k n z_k=na_k\\ a_k=\frac {z_k} n zk​=nak​ak​=nzk​​

所以我们可以求出原来的多项式了。

有几点需要注意：

  • 我们提取 a i a_i ai​ 只提取实部，因为虚部是虚数，无法经过我们的转换后变成实数。
  • 数字有一定误差（毕竟你使用了三角函数等东西，小数是会有误差的），所以要四舍五入。
for(int i=0;i<=len-1;i++)
{
	ans[i]+=floor(a[i].real()/len+0.5);
}

快速傅里叶变换

快速傅里叶变换(Fast Fourier Transform，简称FFT)，是在 DFT的基础上我们发现时间复杂度依然需要 O ( n 2 ) O(n^2) O(n2)，没有含金量，所以我们要给他含金量！

我们可以使用分治的思想，使得时间复杂度降至 O ( n log ⁡ n ) O(n\log n) O(nlogn)。

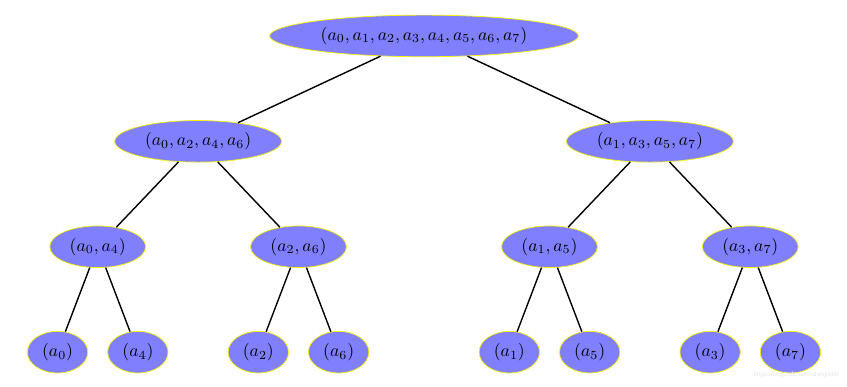
对于 A ( x ) = a 0 + a 1 x + a 2 x 2 + . . . + a n − 1 x n − 1 A(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1} A(x)=a0​+a1​x+a2​x2+...+an−1​xn−1，我们可以：

A 1 ( x ) = a 0 + a 2 x + . . . , A 2 ( x ) = a 1 + a 3 x + . . . A ( x ) = A 1 ( x 2 ) + x A 2 ( x 2 ) A ( ω n k ) = A 1 ( ω n 2 k ) + ω n k A 2 ( ω n 2 k ) A ( ω n k ) = A 1 ( ω n 2 k ) + ω n k A 2 ( ω n 2 k ) A_1(x)=a_0+a_2x+...,A_2(x)=a_1+a_3x+...\\ A(x)=A_1(x^2)+xA_2(x^2)\\ A(\omega_n^k)=A_1(\omega_n^{2k})+\omega_n^kA_2(\omega_n^{2k})\\ A(\omega_n^k)=A_1(\omega_{\frac n 2}^{k})+\omega_n^kA_2(\omega_{\frac n 2}^{k})\\ A1​(x)=a0​+a2​x+...,A2​(x)=a1​+a3​x+...A(x)=A1​(x2)+xA2​(x2)A(ωnk​)=A1​(ωn2k​)+ωnk​A2​(ωn2k​)A(ωnk​)=A1​(ω2n​k​)+ωnk​A2​(ω2n​k​)

同理:

A ( ω n k + n 2 ) = A 1 ( ω n 2 k + n ) + ω n k + n 2 A 2 ( ω n 2 k + n ) A ( ω n k + n 2 ) = A 1 ( ω n 2 k ) − ω n k A 2 ( ω n 2 k ) A(\omega_n^{k+\frac n 2})=A_1(\omega_n^{2k+n})+\omega_n^{k+\frac n 2}A_2(\omega_n^{2k+n})\\ A(\omega_n^{k+\frac n 2})=A_1(\omega_{\frac n 2}^{k})-\omega_n^{k}A_2(\omega_{\frac n 2}^{k})\\ A(ωnk+2n​​)=A1​(ωn2k+n​)+ωnk+2n​​A2​(ωn2k+n​)A(ωnk+2n​​)=A1​(ω2n​k​)−ωnk​A2​(ω2n​k​)

不错！利用这两个式子，我们可以在 O ( n log ⁡ n ) O(n \log n) O(nlogn) 的时间复杂度求出 A ( x ) A(x) A(x)。

不过注意这里一直有一个除二操作，为了方便，我们需要把多项式补成一个次数为 2 x − 1 2^x-1 2x−1 的多项式。

可以写一个递归来求解。

注意这个取倒可以利用共轭复数，对于 a + i b a+ib a+ib，其共轭复数为 a − i b a-ib a−ib。

1 a + i b = a − i b ( a + i b ) ( a − i b ) = a − i b a 2 + b 2 \frac {1}{a+ib}=\frac {a-ib}{(a+ib)(a-ib)}=\frac {a-ib}{a^2+b^2} a+ib1​=(a+ib)(a−ib)a−ib​=a2+b2a−ib​

由于此处 a 2 + b 2 = 1 a^2+b^2=1 a2+b2=1 ,因此其共轭复数为其倒数。

void FFT(cp *a,LL n,bool inv)//inv 表示omega是否取倒
{
	if(n==1)return;
	static cp buf[N];
	LL m=n/2;
	for(int i=0;i<=m-1;i++)buf[i]=a[2*i],buf[i+m]=a[2*i+1];//奇偶分开
	for(int i=0;i<=n-1;i++)a[i]=buf[i];
	FFT(a,m,inv),FFT(a+m,m,inv);
	for(int i=0;i<=m-1;i++)
	{
		cp x=omega(n,i);
		if(inv)x=conj(x);//conj(x)求解共轭复数
		buf[i]=a[i]+x*a[i+m],buf[i+m]=a[i]-x*a[i+m];
	}
	for(int i=0;i<=n-1;i++)a[i]=buf[i];
}

利用FFT求解多项式的乘积

这个还是十分简单的，直接把两个多项式转化为两个长度相同的次数为 2 x − 1 2^x-1 2x−1的多项式。

求解出其傅里叶变换形式之后，对于每个点对应的复数，相乘即可。

为什么呢？

这里有一个误区大家要注意， a i a_i ai​ 不是一个点，而是单纯因为 ω n i \omega_n^i ωni​是一个复数，所以 a i a_i ai​ 才变成了一个复数， a i a_i ai​只是表示 A ( ω n i ) A(\omega_n^i) A(ωni​)的值。

首先我们知道当前的 a i a_i ai​表示的是 A ( ω n i ) A(\omega_n^i) A(ωni​)， b i b_i bi​表示的是 B ( ω n i ) B(\omega_n^i) B(ωni​)，那么我们将两个值直接相乘。

因此多项式相乘以后，我们希望 a i = A ( ω n i ) B ( ω n i ) a_i=A(\omega_n^i)B(\omega_n^i) ai​=A(ωni​)B(ωni​)，那么就是直接相乘喽。

给一个简单的实现：

nclude<bits/stdc++.h>
#define LL int
#define cp complex<double>
using namespace std;
const double PI=acos(-1.0000);
const int N=5e6+5;
cp omega(LL n, LL k)
{
    return cp(cos(2*PI*k/n),sin(2*PI*k/n));
}
LL n,x,len,ans[N];
cp a[N],b[N];
//上文的 FFT 实现省去
int main()
{
	scanf("%d",&n); 
	len=1;
	while(len<2*n)len*=2;
	for(int i=n-1;i>=0;i--)scanf("%1d",&x),a[i].real(x);
	for(int i=n-1;i>=0;i--)scanf("%1d",&x),b[i].real(x);
	FFT(a,len,0),FFT(b,len,0);
	for(int i=0;i<=len-1;i++)a[i]*=b[i];
	FFT(a,len,1);
	for(int i=0;i<=len-1;i++)//进位
	{
		ans[i]+=floor(a[i].real()/len+0.5);
		ans[i+1]+=ans[i]/10;
		ans[i]%=10;
	}
	int i=len;
	for(i;i>=0&&ans[i]==0;i--);//前导零
	if(i==-1)len=0;
	for(;i>=0;i--)printf("%d",ans[i]); 
}

非递归FFT

这里有一个优化，我们发现每次递归有一个把 a i a_i ai​ 奇偶分开的过程，本质来看，就是将二进制末尾为 0 0 0 的数字与二进制末尾为 1 1 1 的数字分开。

我们不妨想一下，对于一个数 x x x，其位置可以根据其二进制确定，就是其二进制倒过来的数字。
img

我们先将每个 a i a_i ai​ 放置在对应的位置，然后向上逐渐合并。

void FFT(cp *a,bool inv)
{
	LL lim=0;
	while((1<<lim)<len)lim++;
	for(int i=0;i<=len-1;i++)
	{
		LL t=0;
		for(int j=0;j<lim;j++)
			if((i>>j)&1)t|=(1<<(lim-j-1));//处理其翻转后的值
		if(i<t)swap(a[i],a[t]);
	}
	static cp buf[N];
	for(int l=2;l<=len;l*=2)
	{
		LL m=l/2;
		for(LL j=0;j<=len-1;j+=l)
		{
			for(LL i=0;i<=m-1;i++)
			{
				cp x=omega(l,i+j);
				if(inv)x=conj(x);
				buf[i+j]=a[i+j]+x*a[i+j+m];
				buf[i+j+m]=a[i+j]-x*a[i+j+m];
			}
		}
		for(int j=0;j<=len-1;j++)a[j]=buf[j];
	}
}

蝴蝶操作

这个东西其实就是想了个办法使得把工具人数组 buf 除掉了。

调调顺序即可。

void FFT(cp *a,bool inv)
{
	LL lim=0;
	while((1<<lim)<len)lim++;
	for(int i=0;i<=len-1;i++)
	{
		LL t=0;
		for(int j=0;j<lim;j++)
			if((i>>j)&1)t|=(1<<(lim-j-1));
		if(i<t)swap(a[i],a[t]);
	}
	for(int l=2;l<=len;l*=2)
	{
		LL m=l/2;
		for(LL j=0;j<=len-1;j+=l)
		{
			for(LL i=0;i<=m-1;i++)
			{
				cp x=omega(l,i+j);
				if(inv)x=conj(x);
				x*=a[i+j+m];
				a[i+j+m]=a[i+j]-x;
				a[i+j]=a[i+j]+x;
			}
		}
	}
}

一些小优化

对于 i i i 的二进制翻转可以先预处理出来，我们用 R i R_i Ri​ 表示 i i i 的二进制翻转。

然后 ω n k \omega_n^k ωnk​ 可以利用性质累乘，会快很多，因为复数的各种操作常数巨大，直接累乘常数较小。

最后代码就长这样了：

#include<bits/stdc++.h>
#define LL int
#define cp complex<double>
using namespace std;
const double PI=acos(-1.0000);
const int N=5e6+5;
cp omega(LL n, LL k)
{
    return cp(cos(2*PI*k/n),sin(2*PI*k/n));
}
LL n,len,lim,x,ans[N],r[N];
cp a[N],b[N];
void FFT(cp *a,bool inv)
{
	for(int i=0;i<=len-1;i++)
	{
		LL t=r[i];
		if(i<t)swap(a[i],a[t]);
	}
	for(int l=2;l<=len;l*=2)
	{
		LL m=l/2;
		cp omg=omega(l,1);
		for(LL j=0;j<=len-1;j+=l)
		{
			cp x(1,0); 
			for(LL i=0;i<=m-1;i++)
			{
				cp t=x;
				if(inv)t=conj(t);
				t*=a[i+j+m];
				a[i+j+m]=a[i+j]-t,a[i+j]=a[i+j]+t;
				x*=omg;
			}
		}
	}
}
int main()
{
	scanf("%d",&n); 
	len=1;
	while(len<2*n)len*=2,lim++;
	for(int i=0;i<=len-1;i++)
	{
		LL t=0;
		for(int j=0;j<lim;j++)if((i>>j)&1)t|=(1<<(lim-j-1));
		r[i]=t;
	}
	for(int i=n-1;i>=0;i--)scanf("%1d",&x),a[i].real(x);
	for(int i=n-1;i>=0;i--)scanf("%1d",&x),b[i].real(x);
	FFT(a,0),FFT(b,0);
	for(int i=0;i<=len-1;i++)a[i]*=b[i];
	FFT(a,1);
	for(int i=0;i<=len-1;i++)
	{
		ans[i]+=floor(a[i].real()/len+0.5);
		ans[i+1]+=ans[i]/10;
		ans[i]%=10;
	}
	int i=len;
	for(i;i>=0&&ans[i]==0;i--);
	if(i==-1)len=0;
	for(;i>=0;i--)printf("%d",ans[i]);
}

参考

胡小兔-小学生都能看懂的FFT！！！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/477021.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

java结束当前循环

java结束当前循环

在 Java中&#xff0c;当我们要结束一个循环时&#xff0c;通常会使用循环变量的实现类来结束&#xff0c;但在实际开发中&#xff0c;我们经常会遇到某个循环结束后需要进行其他的操作的情况。此时&#xff0c;就需要使用循环变量来结束当前循环。 1、创建一个新的类&#xff…
阅读更多...
数据结构_双链表、循环链表、静态链表

数据结构_双链表、循环链表、静态链表

目录 1. 双链表 1.1 双链表的初始化 1.2 双链表的插入操作 1.3 双链表的删除操作 1.4 双链表的遍历 2. 循环链表 2.1 循环单链表 2.2 循环双链表 3. 静态链表 4. 顺序表和链表的比较 5. 相关练习 1. 双链表 单链表结点中只有一个指向其后继的指针&#xff0c;使得单…
阅读更多...
电子电气架构——车辆E/E架构软硬件解耦

电子电气架构——车辆E/E架构软硬件解耦

我是穿拖鞋的汉子，魔都中坚持长期主义的工程师。 老规矩，分享一段喜欢的文字，避免自己成为高知识低文化的工程师： 人只有在举棋不定，无从把握的时候才感到疲惫。只有去行动就能获得解放，哪怕做的不好也比无所作为强！ 本文主要介绍车辆E/E架构常识，主要涉及内容是行业最…
阅读更多...
Python实现LBP纹理提取

Python实现LBP纹理提取

1、什么是LBP纹理特征&#xff1f; LBP&#xff08;Local Binary Patterns&#xff0c;局部二值模式&#xff09;是提取局部特征作为判别依据的&#xff0c;一种有效的纹理描述算子&#xff0c;度量和提取图像局部的纹理信息。它具有旋转不变性和灰度不变性等显著的优点&#…
阅读更多...
uniapp中使用vuex（解决uniapp无法在data和template中获取vuex数据问题）

uniapp中使用vuex（解决uniapp无法在data和template中获取vuex数据问题）

uniapp中使用vuex&#xff08;解决uniapp无法在data和template中获取vuex数据问题&#xff09; 1. uniapp中引入vuex2. uniapp中使用vuex3. 解决uniapp无法在data和template中获取vuex数据问题 1. uniapp中引入vuex 1 .在根目录下新建文件夹store,在此目录下新建index.js文件&…
阅读更多...
第五章——动态规划3

第五章——动态规划3

蒙德里安的梦想 我们在黑框内横着放红框&#xff0c;我们发现当横向小方格摆好之后&#xff0c;纵向小方格只能一次纵向摆好&#xff0c;即纵向小方格只有一种方案&#xff0c;即整个摆放小方格的方案数等于横着摆放小方格的方案数 f[i,j]表示的是现在要在第i列摆&#xff0c;j…
阅读更多...
代码随想录Day64（一刷完结）

代码随想录Day64（一刷完结）

今天学习单调栈解决最后一道题 84.柱状图中的最大矩形 给定 n 个非负整数&#xff0c;用来表示柱状图中各个柱子的高度。每个柱子彼此相邻&#xff0c;且宽度为 1 。 求在该柱状图中&#xff0c;能够勾勒出来的矩形的最大面积。 示例 1: 输入&#xff1a;heights [2,1,5,6,…
阅读更多...
C++中的list容器

C++中的list容器

文章目录 list的介绍list的使用list的构造list iterator的使用list capacitylist元素访问list modifierslist的迭代器失效 list与vector的对比 list的介绍 list是可以在常数范围内的任意位置进行插入和删除的序列式容器&#xff0c;并且该容器可以前后双向迭代&#xff1b;   …
阅读更多...
FFMPEG中的filter使用二

FFMPEG中的filter使用二

上一篇我们在使用滤镜时是手动创建各种滤镜&#xff0c;然后根据处理链路手动链接不同的过滤器&#xff0c;有助于我们理解滤镜的流程。这一篇我们使用参数形式&#xff0c;让ffmpeg自动帮我们创建和链接过滤器&#xff0c;这样可以减少代码量&#xff0c;同时我们可以先使用参…
阅读更多...
学系统集成项目管理工程师（中项）系列15_质量管理

学系统集成项目管理工程师（中项）系列15_质量管理

1. 质量&#xff08;Quality&#xff09;的定义 1.1. 反应实体满足主体明确和隐含需求的能力的特性总和 1.2. 明确需求是指在标准、规范、图样、技术要求、合同和其他文件中用户明确提出的要求与需要 1.3. 隐含需求是指用户和社会通过市场调研对实体的期望以及公认的、不必明…
阅读更多...
thinkphp路由，请求和响应

thinkphp路由，请求和响应

文章目录 定义获取路由后面的参数跨域请求请求响应 定义 thinkphp定义路由一般在route路由下的app.php中 下面这是一个简单的路由 Route::rule(admin/login,/app/controller/Admin/login)->middleware(\app\middleware\MyMiddleware::class);该路由表示当访问admin/login时…
阅读更多...
人工智能课程笔记（7）强化学习（基本概念 Q学习 深度强化学习 附有大量例题）

人工智能课程笔记（7）强化学习（基本概念 Q学习 深度强化学习 附有大量例题）

文章目录 1.强化学习与深度学习的区别2.强化学习中的基本概念3.强化学习、有监督学习和无监督学习的区别4.强化学习的特点5.离散马尔可夫过程6.马尔可夫奖励过程7.马尔可夫决策过程8.策略学习8.1.策略学习概念8.2.策略评估与贝尔曼方程 9.强化学习的最优策略求解10.基于价值的强…
阅读更多...
K8s基础1——发展起源、资源对象、集群架构

K8s基础1——发展起源、资源对象、集群架构

文章目录 一、发展起源二、资源对象2.1 集群类2.2 应用类2.3 存储类2.4 安全类 三、集群架构 一、发展起源 K8s官方文档 K8s怎么来的&#xff1f; 十几年来&#xff0c;谷歌内部使用的大规模集群管理系统是Brog&#xff0c;基于容器技术实现了资源管理的自动化和跨多个数据中心…
阅读更多...
基于Python的连锁超市收银系统的开发与研究_kaic

基于Python的连锁超市收银系统的开发与研究_kaic

基于Python的连锁超市收银系统的开发与研究 摘要&#xff1a;近几年来&#xff0c;国内的连锁超市收银系统也在不断的发展与完善&#xff0c;超市收银系统是一个超市管理的核心&#xff0c;他决定了超市的安全性。目前&#xff0c;大大小小的超市基本上由传统的人工管理逐渐过渡…
阅读更多...
IT 面试手册 - 序

IT 面试手册 - 序

IT 面试手册 - 序 前言 首先&#xff0c;感谢你阅读我的文章。作为在计算机互联网行业摸爬滚打近十载的半个过来人&#xff0c;在这里分享一些关于求职面试和自我提升的心得感悟&#xff0c;希望能够给你一些启发。 背景 对于 IT 从业者来说&#xff0c;当今这个时代&#x…
阅读更多...
Docker的四种网络模式

Docker的四种网络模式

1.Host 模式 通常来讲&#xff0c;启动新的Docker容器&#xff0c;都会分配独立的Network Namespace隔离子系统&#xff0c;如果在运行是指定为host模式&#xff0c;那么Docker容器将不会获得一个独立的Network Namespace&#xff0c;而是和宿主机共用一个Network Namespace子…
阅读更多...
计算机网络知识复习

计算机网络知识复习

目录 TCP/IP协议群做了哪些事情&#xff1f; TCP协议为什么是3次握手&#xff0c;4次挥手&#xff1f; 如果网络延迟是30ms&#xff0c;那么Ping(基于UDP的)一个网站需要多少ms&#xff1f; 如果请求一个HTTP协议的网站&#xff0c;TTFB至少ms&#xff1f; CDN更换图片&am…
阅读更多...
WeakMap 与 WeakSet

WeakMap 与 WeakSet

WeakSet WeakSet 结构与 Set 类似&#xff0c;也是不重复的值的集合。 成员都是数组和类似数组的对象&#xff0c;WeakSet 的成员只能是对象&#xff0c;而不能是其他类型的值。 若调用 add() 方法时传入了非数组和类似数组的对象的参数&#xff0c;就会抛出错误。 const b …
阅读更多...
Linux进程间通信 - 信号(signal) 与 管道(pipe) 与 消息队列

Linux进程间通信 - 信号(signal) 与 管道(pipe) 与 消息队列

什么是进程间通信&#xff0c;就是进程与进程之间进行通信&#xff0c;互相发送消息&#xff1b;可以通过 信号 或者 管道 或者 消息队列 或者 信号量 去通信&#xff01; 目录 一、信号 1. 信号简介 2. 都有那些信号&#xff1f; 3. 注册信号的函数 1). signal 2). sig…
阅读更多...
十一、通过六个因素对织物起球等级进行预测

十一、通过六个因素对织物起球等级进行预测

一、需求分析 根据之前做训练的模型&#xff0c;对不同等级的标准样卡进行测试 测试样本有48张&#xff0c;其中包括起球个数、起球总面积、起球最大面积、起球平均面积、对比度、光学体积六个指标&#xff0c;最终确定出织物的等级 数据集fiber.csv大致结构如下&#xff1a; …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023