蒙德里安的梦想


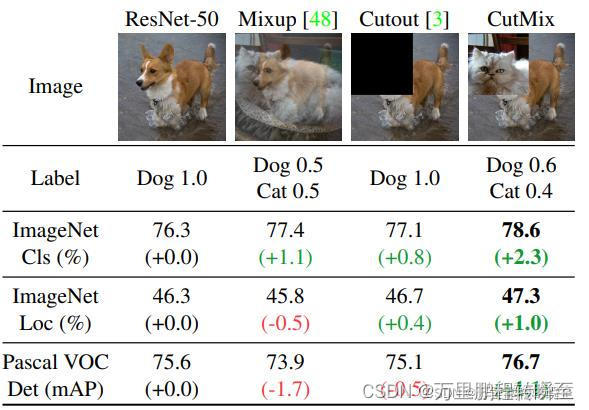
我们在黑框内横着放红框,我们发现当横向小方格摆好之后,纵向小方格只能一次纵向摆好,即纵向小方格只有一种方案,即整个摆放小方格的方案数等于横着摆放小方格的方案数

f[i,j]表示的是现在要在第i列摆,j代表二进制数,这里总共有五列,2^5次方,j的10进制范围从0-31,
在下图中 ,i在第二列,j统计的是i前面的列是否伸出小方格到第i列,第一行有是1,第二行没有是0,第三行没有是0第四行有是1,第五行没有是0,j表示为10010

我们要计算f[i,j]先计算第i-1列的状态,前一列记作f[i-1,k]
我们首先要保证不冲突,即小方格必须是1x2的,不能超过题目要求范围,用(j&k)进行位运算来判断

其次要保证所有连续的空白格子,一定得是偶数,不然没法竖着填,下图中第i-1列第三行是奇数,就导致那个格子不能竖着填(我们这里的目的是只枚举横向格子,剩下的格子用纵向的来填),即j|k不能存在连续奇数个0。

其他优秀博主的相关博客
点击跳转1
点击跳转2
点击跳转3
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 12, M = 1 << N;
int n, m;//n,m分别代表矩形的行数,列数
long long f[N][M];//f是状态转移的方程
bool st[M];//st表示
int main()
{
while (cin >> n >> m, n || m)//读入n和m,并且不是两个0即合法输入就继续读入
{
// 循环2的n次方次,处理st数组?---------------问题一:为什么是2的n次方次循环
// 这个循环其实表示的是每列的每种状态,如i = 1011下,当前这一列空着的连续块是不是2的偶数倍
// 因为对于每一行,都有选和不选两种情况,则对n行,有2的n次方种选法,则要循环2的n次方次
memset(f,0,sizeof f);//把f置成0
for (int i = 0; i < 1 << n; i++)
{
st[i] = true;
int cnt = 0;//表示当前连续0的个数
for (int j = 0; j < n; j++)
if (i >> j & 1)//如果当前这位是1,说明上一段已经截止
//i 右移 j 位与上 1 ,这行代码是判断第 j 位上是不是1,如果是1了,表明这位上不是0,则进一步去判断前一段的连续的0是不是偶数个
{
if (cnt & 1) st[i] = false;//看上一段连续的0是否有奇数个,如果有则不合法
cnt = 0;//连续的已经结束,把cnt清为0
}
else cnt++;
if (cnt & 1) st[i] = false;//最后一段如果是连续奇数,就改成false
}
//DP过程
f[0][0] = 1;//第0列前面没有任何列,所以f[0][0]是1
//枚举所有的列
for (int i = 1; i <= m; i++)
for (int j = 0;j < 1<< n; j++)
for (int k = 0; k < 1 << n; k++)
if ((j & k) == 0 && st[j | k])
f[i][j] += f[i - 1][k];
cout << f[m][0] << endl;
}
return 0;
}最短Hamilton路径
题目描述
给定一张 n 个点的带权无向图,点从 0∼n−1 标号,求起点 0 到终点 n−1 的最短 Hamilton 路径。
Hamilton 路径的定义是从 0 到 n−1 不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数 n。
接下来 n 行每行 n 个整数,其中第 i 行第 j 个整数表示点 i 到 j 的距离(记为 a[i,j])。
对于任意的 x,y,z,数据保证 a[x,x]=0,a[x,y]=a[y,x] 并且 a[x,y]+a[y,z]≥a[x,z]。
输出格式
输出一个整数,表示最短 Hamilton 路径的长度。
数据范围
1≤n≤20
0≤a[i,j]≤10^7
输入样例:
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
输出样例:
18
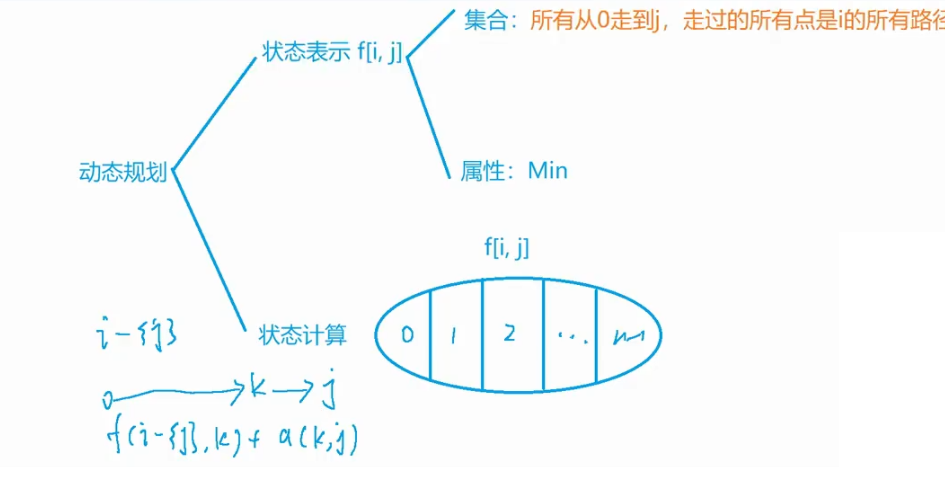
f[i,j]表示所有从0走到j,走过的所有点是i的所有路径,i用二进制表示,表示的是当前的这个点是否走过了,若i=1110011表示第0,1点走过了2,3点没走过,4,5,6点走过了。
所有路径都是从0走到j,中间走过的所有点是i,我们用倒数第二个点来分类,倒数第二个点是0,表示第一类,是1,表示第二类……n-1表示最后一类,从0到j,可看作0到k,k到j,其中k到j是固定的,我们只需要求0到k的最短路径即可。
从0到j走过的所有点是i,从0到k走过的所有点是i-j这个点,即

const int N = 20, M = 1 << N;
int n;
int w[N][N];//俩点间的距离
int f[M][N];//存储状态
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cin >> w[i][j];//保存值
memset(f, 0x3f, sizeof f);
f[1][0] = 0;//从0走到0只走过了这一个点,第0位上是1,其余所有位都是0
for (int i = 0; i < 1 << n; i++)
for (int j = 0; j < n; j++)
if (i >> j & 1)
for (int k = 0; k < n; k++)
if ((i - (1 << j)) >> k & 1)
f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]);
cout << f[(1 << n)-1][n - 1] << endl;
return 0;
}热特热你