文章目录
- 一、前言
- 二、SPFA 算法
- 1、SPFA算法的基本流程
- 2、代码详解
- 三、SPFA 算法已死 ?
一、前言
SPFA算法,全称为Shortest Path Faster Algorithm,是求解单源最短路径问题的一种常用算法,它可以处理有向图或者无向图,边权可以是正数、负数,但是不能有负环。
二、SPFA 算法
1、SPFA算法的基本流程
1. 初始化
首先我们需要起点s到其他顶点的距离初始化为一个很大的值(比如9999999,像是 JAVA 中可以设置 Integer.MAX_VALUE 来使),并将起点s的距离初始化为0。同时,我们还需要将起点s入队。
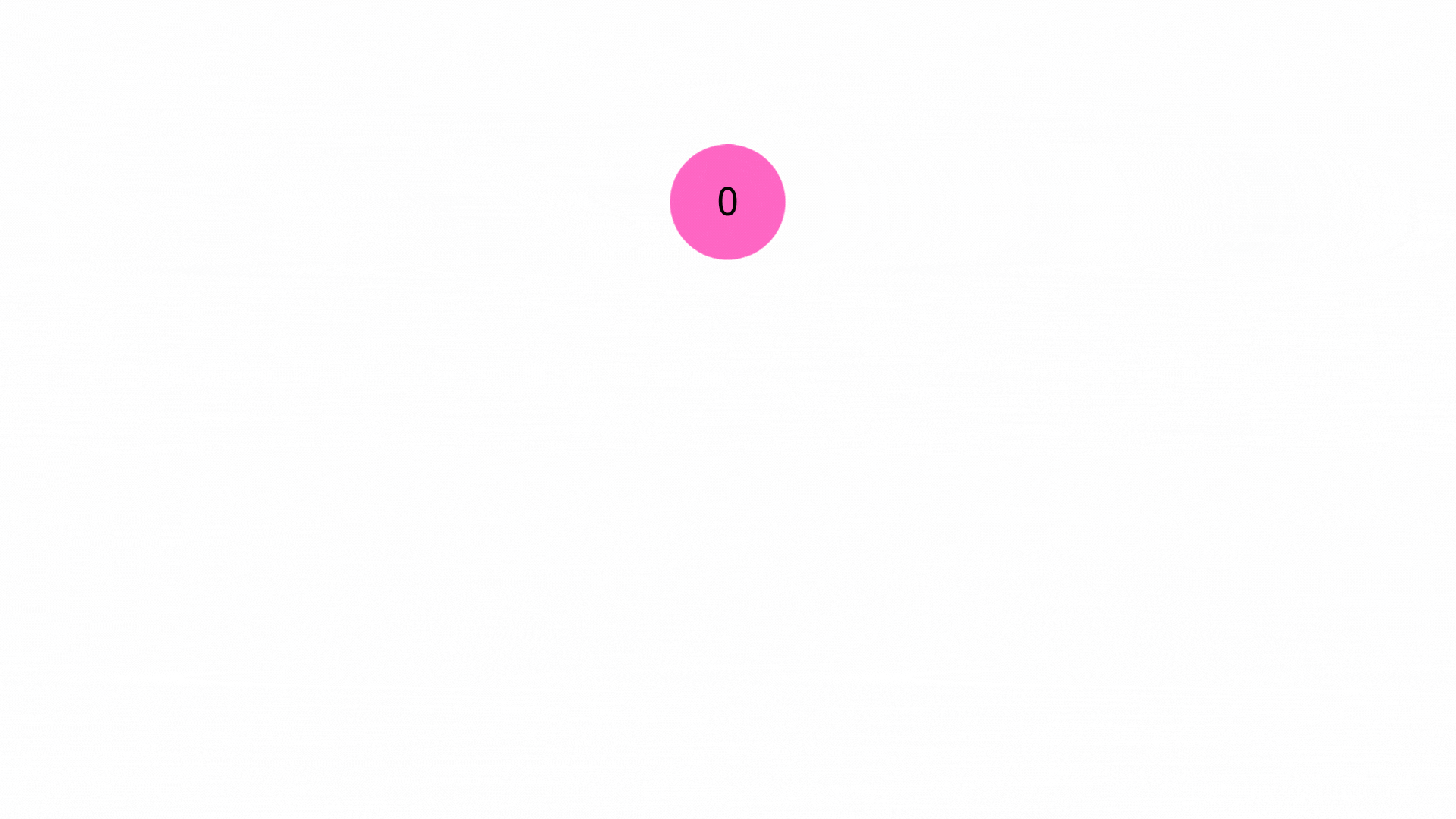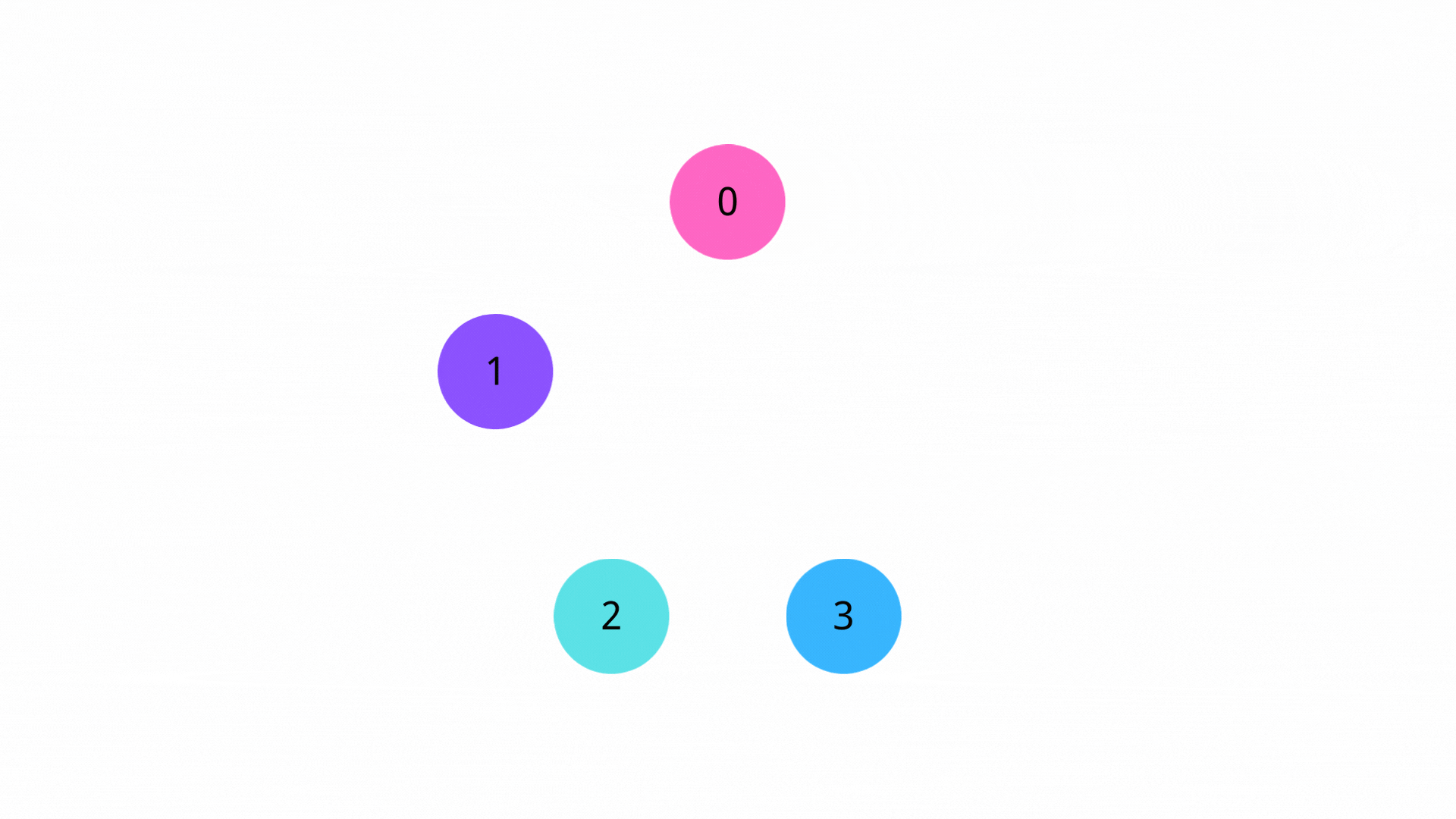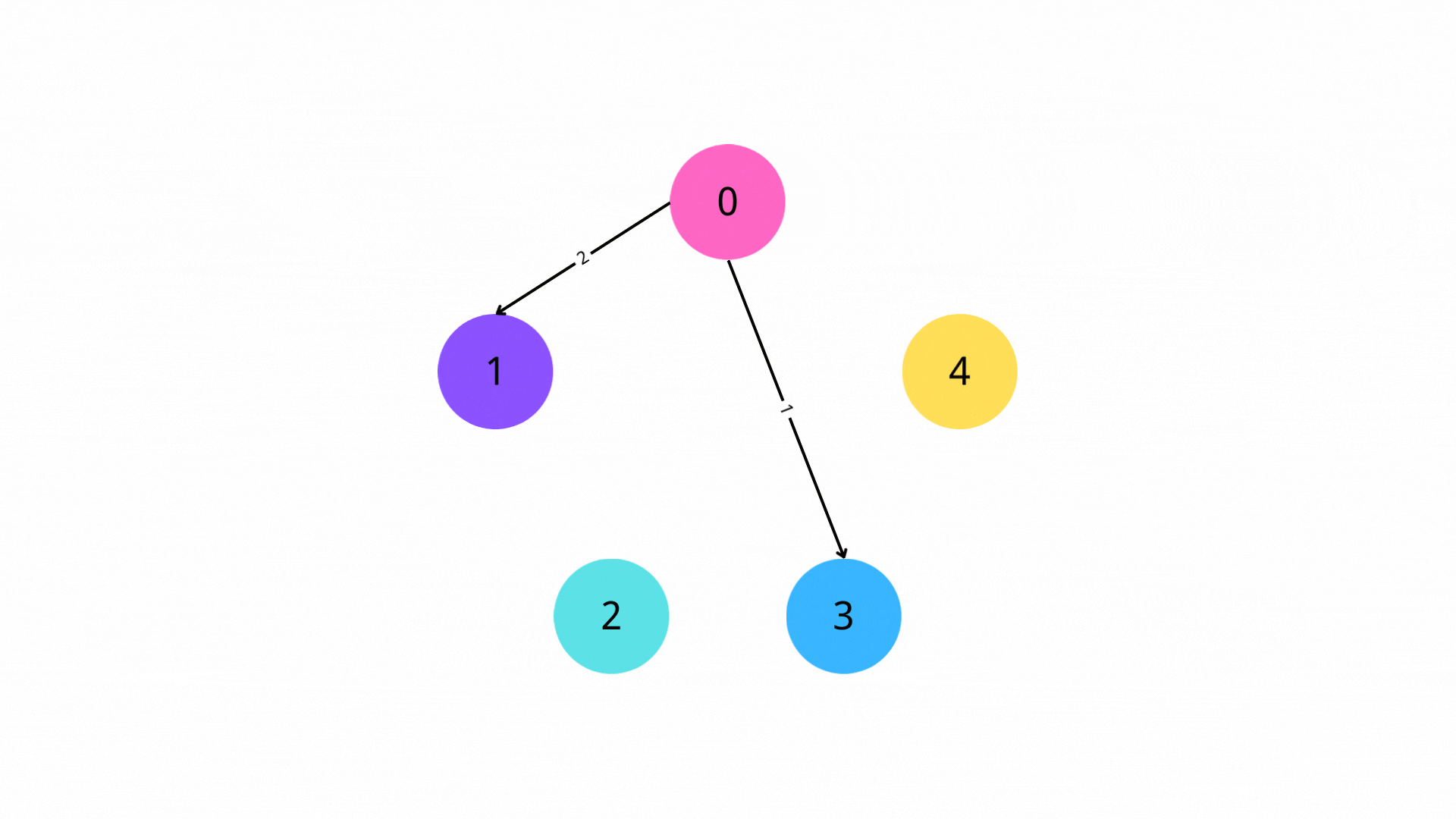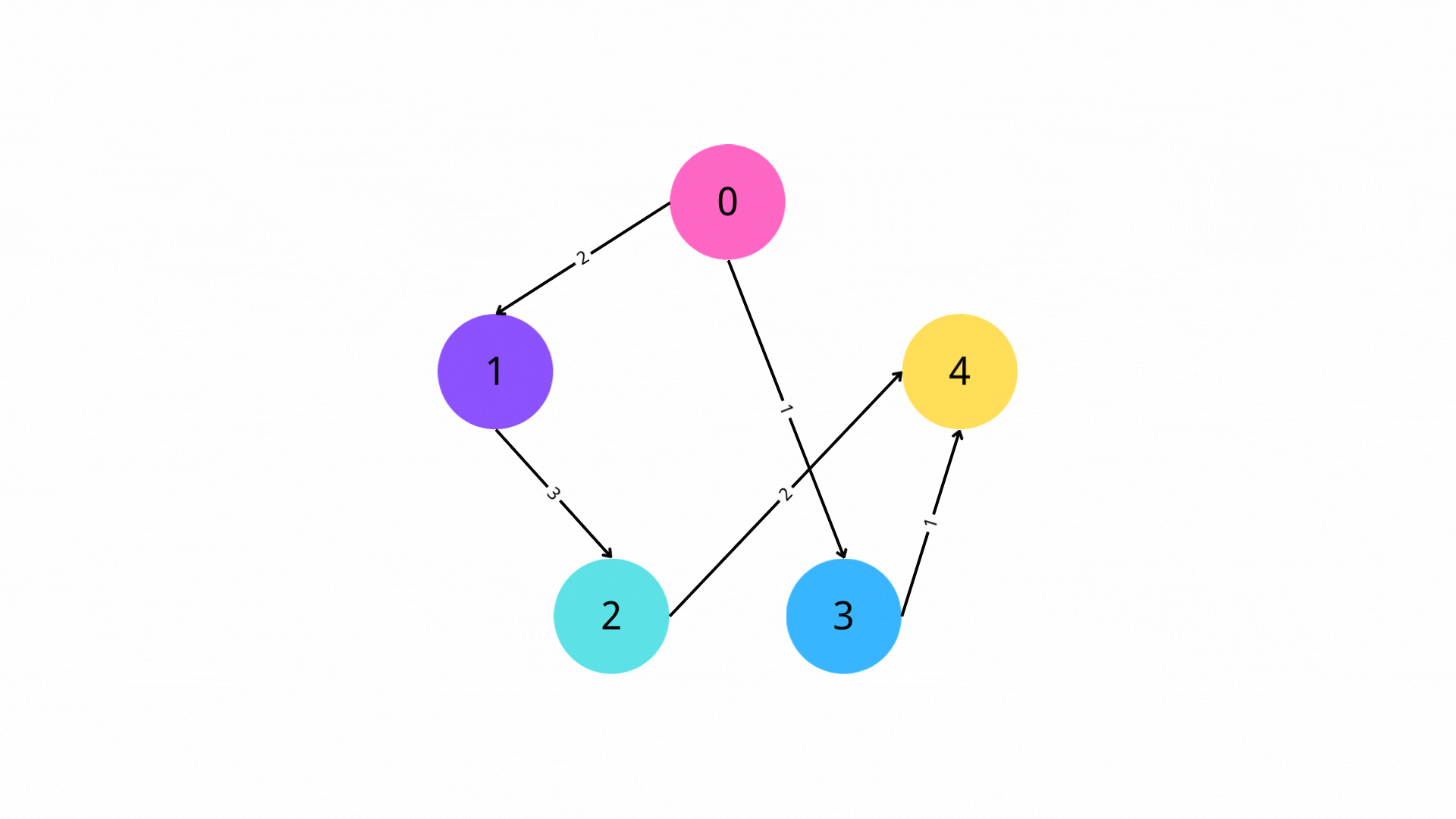
2. 迭代
每次从队列中取出一个顶点u,遍历所有从u出发的边,对于边(u,v)(其中v为从u可以到达的顶点),如果s->u->v的路径长度小于s->v的路径长度,那么我们就更新s->v的路径长度,并将v入队。
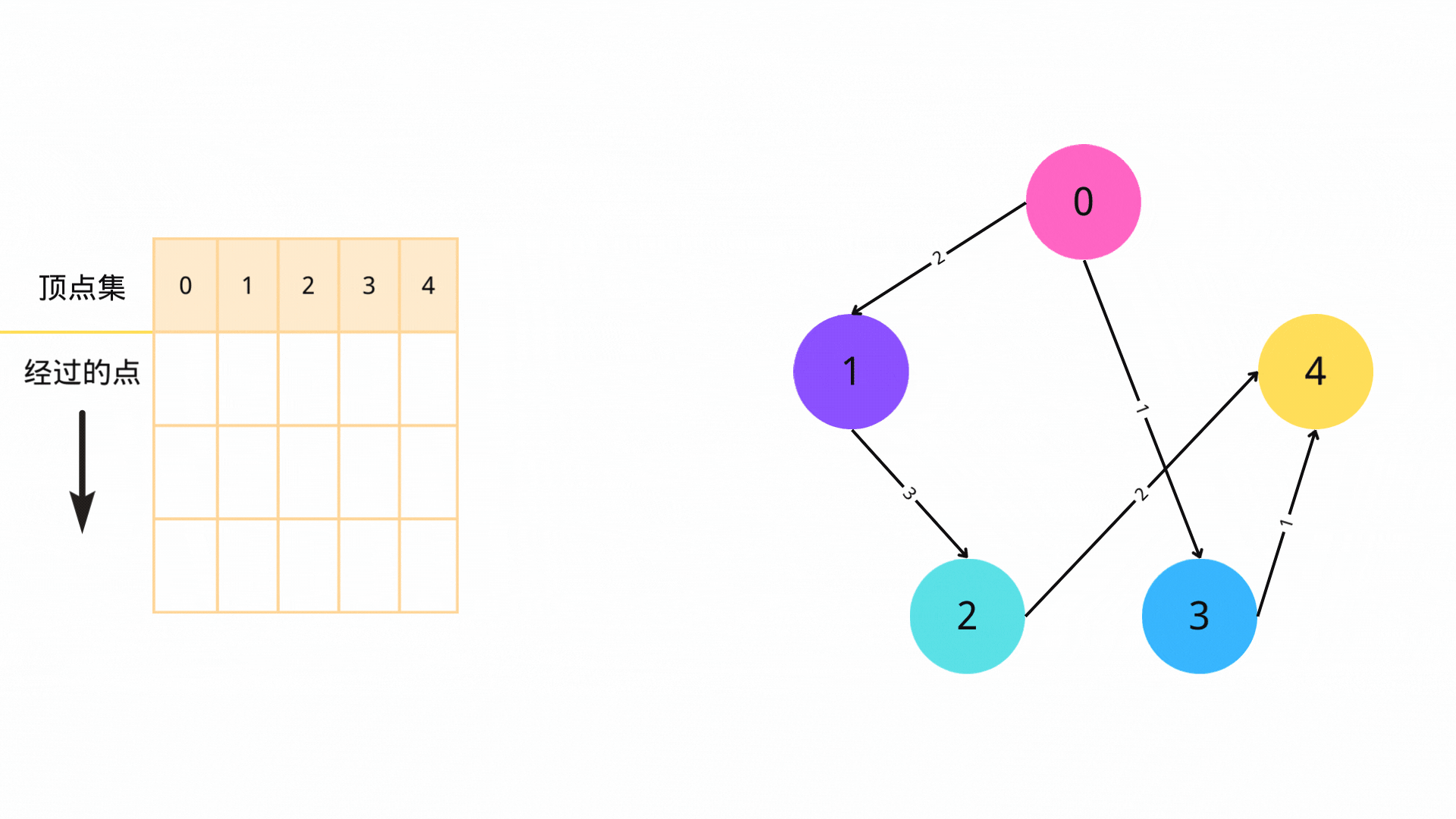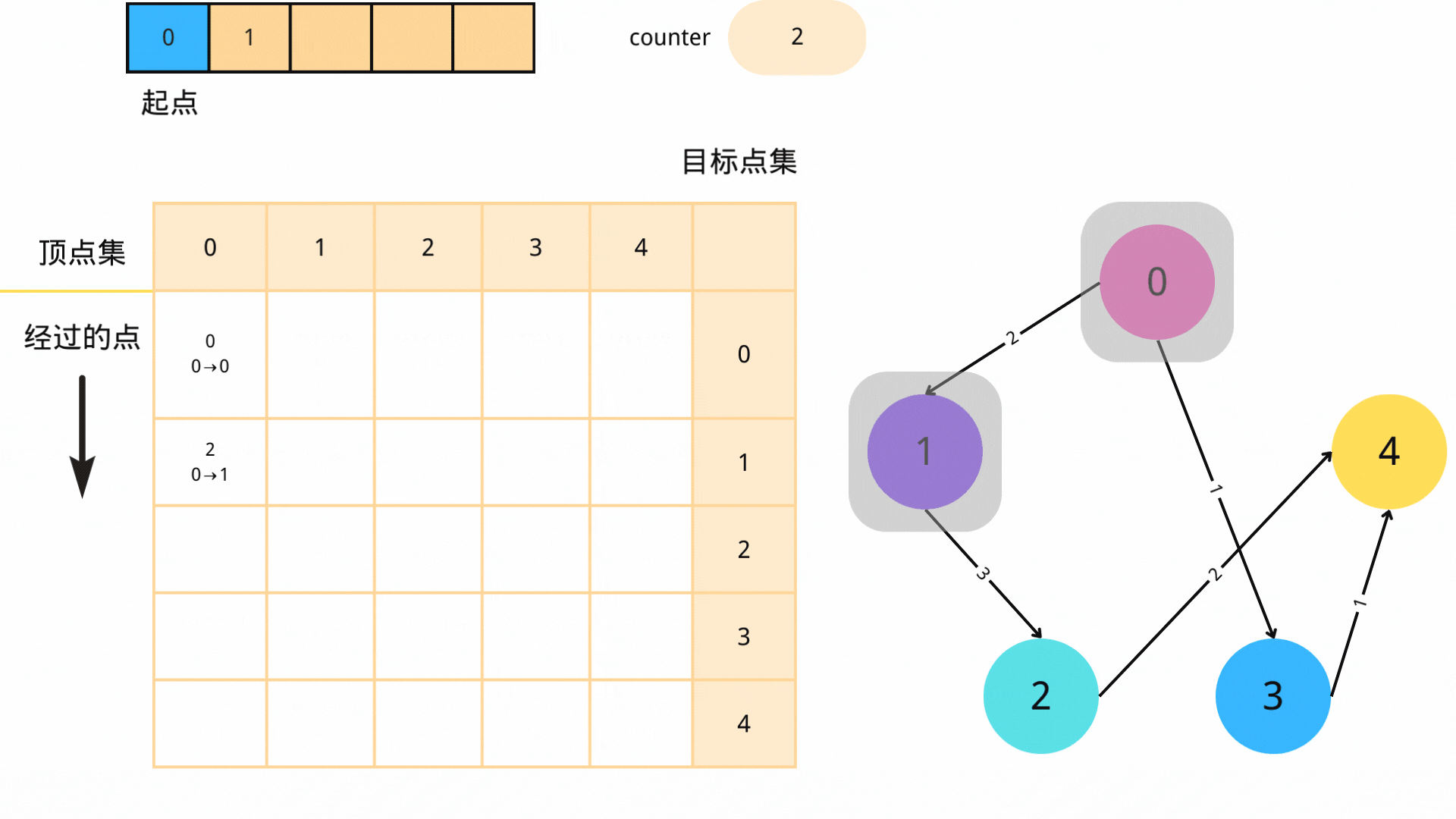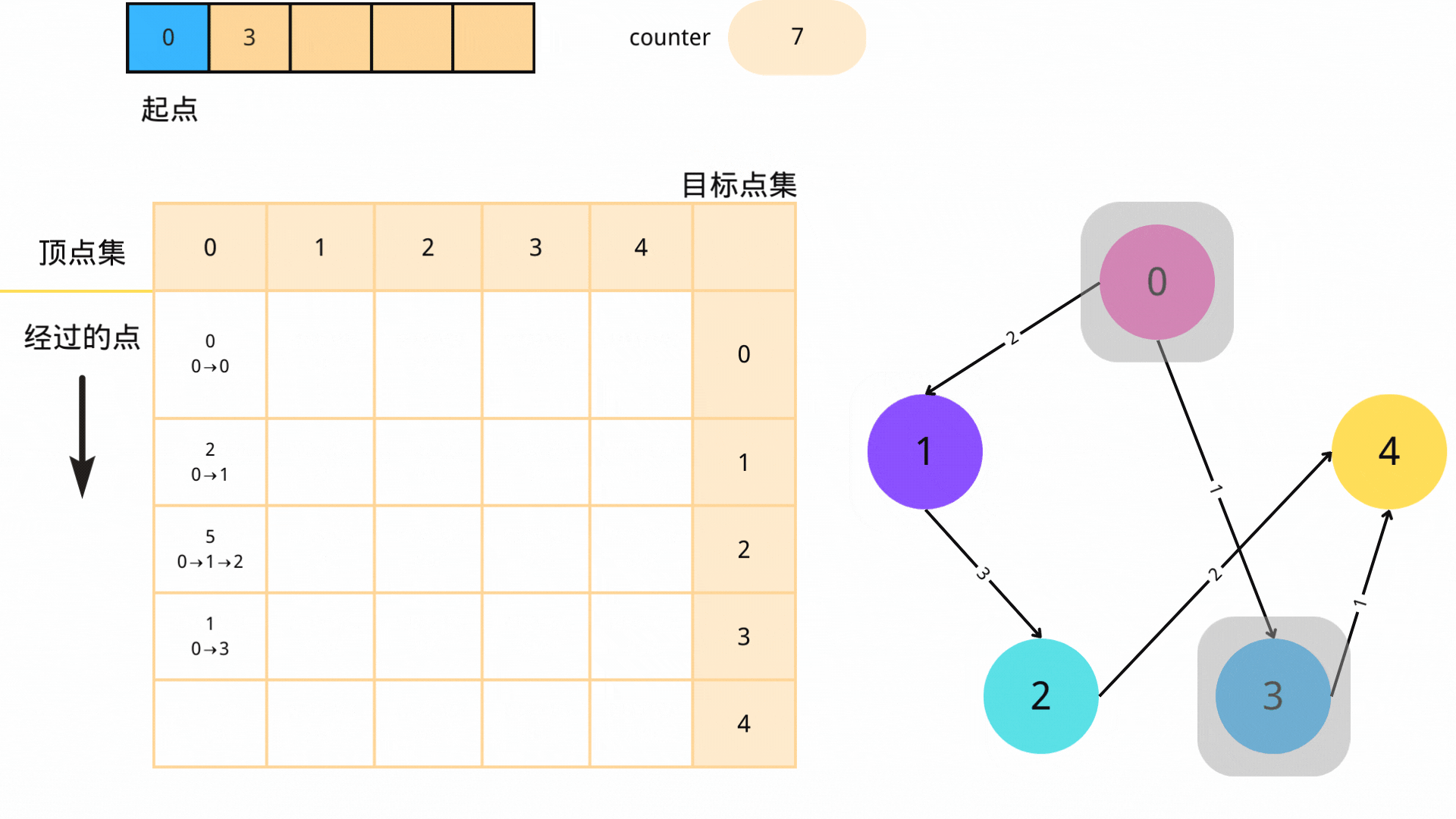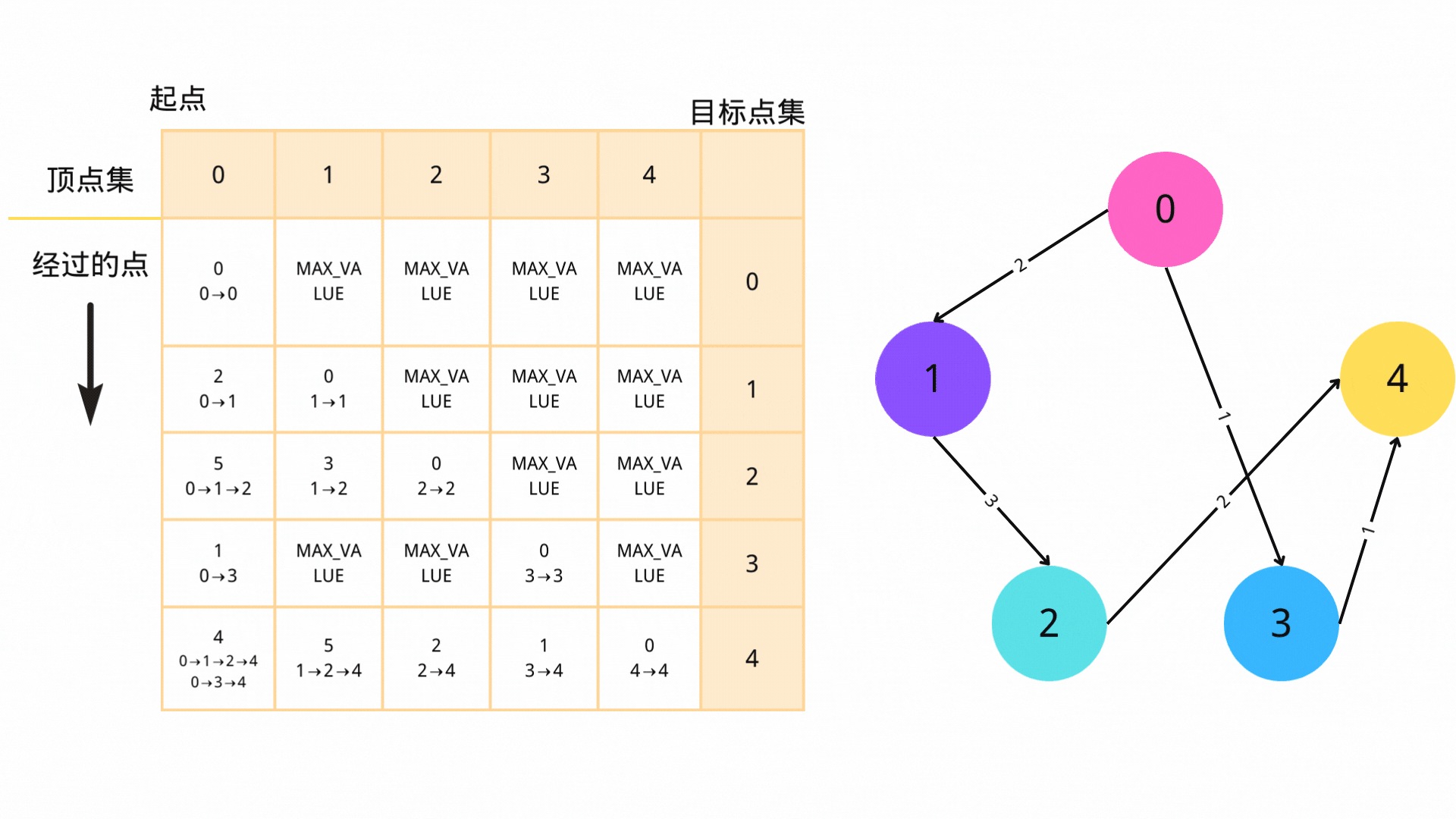
3. 循环
不断进行步骤2,直到队列为空。
4. 判断
最后,我们可以得到从起点s到各个顶点的最短路径长度,如果存在无穷小的距离,则说明从起点s无法到达该顶点。
其次,需要注意的是,SPFA算法中存在负环问题。如果存在负环,则算法会陷入死循环。因此,我们需要添加一个计数器,记录每个点进队列的次数。当一个点进队列的次数超过图中节点个数时,就可以判定存在负环。
2、代码详解
以下是使用Java实现 SPFA算法的代码,其中Graph类表示有向图或无向图,Vertex类表示图中的一个顶点,Edge类表示图中的一条边。
import java.util.*;
class Graph { // 图
private List<Vertex> vertices; // 顶点集
public Graph() {
vertices = new ArrayList<Vertex>();
}
public void addVertex(Vertex v) { // 添加顶点
vertices.add(v);
} // 添加顶点
public List<Vertex> getVertices() { // 返回顶点
return vertices;
} // 获取顶点集
}
class Vertex { // 点
private int id; // 点 id
private List<Edge> edges; // 连接到该顶点的边
private int distance; // 从源顶点到该顶点的最短距离,MAX_VALUE init
private boolean visited; // 在图的遍历过程中是否访问过该顶点,false init
public Vertex(int id) {
this.id = id;
edges = new ArrayList<Edge>();
distance = Integer.MAX_VALUE;
visited = false;
}
public int getId() { // 获取 id
return id;
}
public void addEdge(Edge e) { // 将连接到该顶点边添加到列表中
edges.add(e);
} // 添加图到边
public List<Edge> getEdges() { // 获取连接到该顶点的边集
return edges;
} // 获取图中边
public int getDistance() { // 获取从源顶点到该顶点的最短距离
return distance;
} // 获取源顶点到该顶点的最短距离
public void setDistance(int distance) { //设置最短距离
this.distance = distance;
} // 设置源顶点到该顶点的最短距离
public boolean isVisited() { // 获取在图的遍历过程中是否访问过该点
return visited;
} // 获取图遍历过程中是否访问过该点
public void setVisited(boolean visited) { // 设置在图的遍历过程中是否访问过该点
this.visited = visited;
} // 设置图遍历过程中是否访问过该点
}
class Edge { // 边
private Vertex source; // 源顶点
private Vertex destination; // 目标顶点
private int weight; // 边的权重
public Edge(Vertex source, Vertex destination, int weight) {
this.source = source;
this.destination = destination;
this.weight = weight;
}
public Vertex getSource() { // 返回源顶点
return source;
} // 获取源点
public Vertex getDestination() { // 返回目标顶点
return destination;
} // 获取目标顶点
public int getWeight() { // 获取边的权重
return weight;
} // 获取边的权重
}
// SPFA 算法
public class SPFA {
public static void spfa(Graph graph, Vertex source) {
// 初始化
Queue<Vertex> queue = new LinkedList<Vertex>(); // 初始化一个顶点队列,使用该队列来跟中需要处理的顶点
for (Vertex v : graph.getVertices()) { // 初始化最短距离和是否访问过该点
v.setDistance(Integer.MAX_VALUE);
v.setVisited(false);
}
source.setDistance(0); // 将源顶点到自身的最短距离设为0
queue.add(source); // 将源顶点添加到队列中
// 迭代
int count = 0; // 用于检测图中的负环,count超过图中顶点的总数,抛出异常
// 查找从一个源顶点到图中所有其它顶点的最短路径
while (!queue.isEmpty()) {
Vertex u = queue.poll(); // 存储SPFA算法正在处理的顶点,poll 方法将下一个顶点从队列中取出
u.setVisited(false); // 标记该顶点为未访问,以便在算法中再次对其处理
// 查找部分,循环遍历当前顶点 u 的所有边
for (Edge e : u.getEdges()) {
Vertex v = e.getDestination(); // 返回边 e 的目标顶点给 v
int distance = u.getDistance() + e.getWeight(); // 计算源顶点到目标顶点的距离
if (distance < v.getDistance()) {
v.setDistance(distance); // 更新最短距离
if (!v.isVisited()) { // 如果该顶点未被访问过
queue.add(v); // 将该顶点添加到队列中
v.setVisited(true); // 标记该顶点已被访问
count++; // 负环 + 1
if (count > graph.getVertices().size()) { // 检查 SPFA 算法处理的顶点数是否大于图中顶点总数
throw new RuntimeException("Negative cycle detected");
}
}
}
}
}
}
public static void main(String[] args) {
// 构造图
Graph graph = new Graph();
// 构造顶点
Vertex s = new Vertex(0);
Vertex a = new Vertex(1);
Vertex b = new Vertex(2);
Vertex c = new Vertex(3);
Vertex d = new Vertex(4);
// 点加边
s.addEdge(new Edge(s, a, 2));
s.addEdge(new Edge(s, c, 1));
a.addEdge(new Edge(a, b, 3));
b.addEdge(new Edge(b, d, 2));
c.addEdge(new Edge(c, d, 1));
// 边加点
graph.addVertex(s);
graph.addVertex(a);
graph.addVertex(b);
graph.addVertex(c);
graph.addVertex(d);
// 调用SPFA算法求解最短路径
spfa(graph, s);
// 输出结果
for (Vertex v :graph.getVertices()) {
System.out.println("Shortest distance from source to vertex " + v.getId() + " is " + v.getDistance());
}
}
}
上面的代码实现了SPFA算法,并计算了从给定源点到图中其他所有顶点的最短路径。主要思路如下:
- 初始化:将所有顶点的距离设置为正无穷,将源点的距离设置为0,将源点加入队列。
- 迭代:从队列中取出一个顶点u,遍历它的所有邻居v。如果u到源点的距离加上u到v的边的权重小于v的距离,则更新v的距离,并将v加入队列中。如果v已经在队列中,则不需要再次添加。
- 如果队列为空,则算法结束。如果队列非空,则回到步骤2。
SPFA算法的时间复杂度取决于负权边的数量。如果图中没有负权边,算法的时间复杂度是O(E),其中E是边的数量。但是如果图中有负权边,算法的时间复杂度将达到O(VE),其中V是顶点的数量,E是边的数量。因此,为了避免算法的时间复杂度变得非常高,应尽可能避免在图中使用负权边。
三、SPFA 算法已死 ?
这个问题引发了很多OI选手和出题人的讨论,虽然 SPFA 算法在实际应用中具有一定的优势,但它也有一些缺点,导致它被称为"已死"的算法之一。以下是几个原因:
-
可能会进入负环:SPFA 算法可以处理负权边,但是如果有负权环,算法将无法结束,因为每次都会沿着负权环一遍一遍地更新距离,导致算法陷入死循环。
-
时间复杂度不稳定:在最坏情况下,SPFA 算法的时间复杂度可以达到 O ( V E ) O(VE) O(VE),其中 V V V 和 E E E 分别是图中的顶点数和边数。而在最好情况下,时间复杂度只有 O ( E ) O(E) O(E)。因此,SPFA 算法的时间复杂度是不稳定的。
-
存在更好的算法:对于单源最短路径问题,已经有更好的算法出现,如 Dijkstra 算法和 Bellman-Ford 算法。这些算法在时间复杂度和稳定性方面都比 SPFA 算法更优秀。
虽然 SPFA 算法在某些情况下可以发挥出优势,但是它的缺点也是无法忽视的,而且已经有更好的算法出现,不少大佬也或多或少的对 SPFA 算法进行了优化,更多优化的内容以及最短路径算法可以在论文中找到。因此,SPFA 算法已经不是首选算法,也可以说是已经“死亡”了。