本文是Quantitative Methods and Analysis: Pairs Trading此书的读书笔记。

白噪声（white noise)是最简单的随机时间序列（stochastic time series)。

在每一时刻，从一个正态分布中抽取一个值从而形成白噪声时间序列。并且，这个正态分布的参数是固定的，不会随着时间变化。所以，这种情况就是从一个固定的概率分布中重复抽取值形成时间序列。用表示在时刻抽取的值，所以在时刻时间序列的值。最广泛使用的的白噪声是来自标准正态分布或者说高斯分布（即白噪声序列中的每一项都是从高斯分布中抽样而来，又一种说法就是这种白噪声服从高斯分布），称为高斯白噪声（Gaussian white noise）。

下图分别是一个白噪声时间序列，以及这个白噪声的自相关函数。

 

 

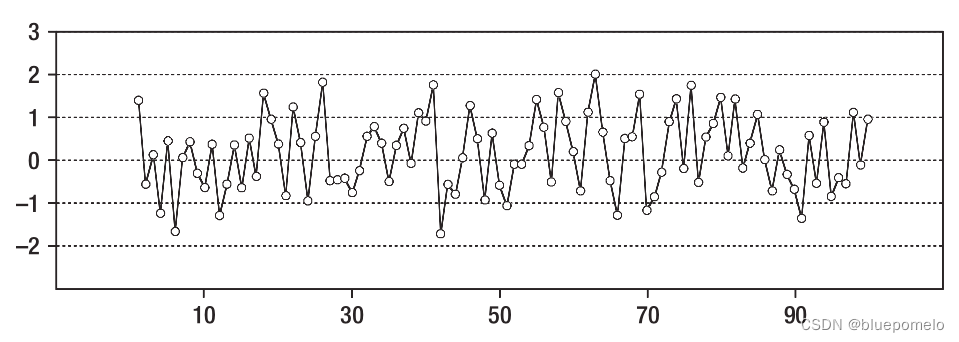
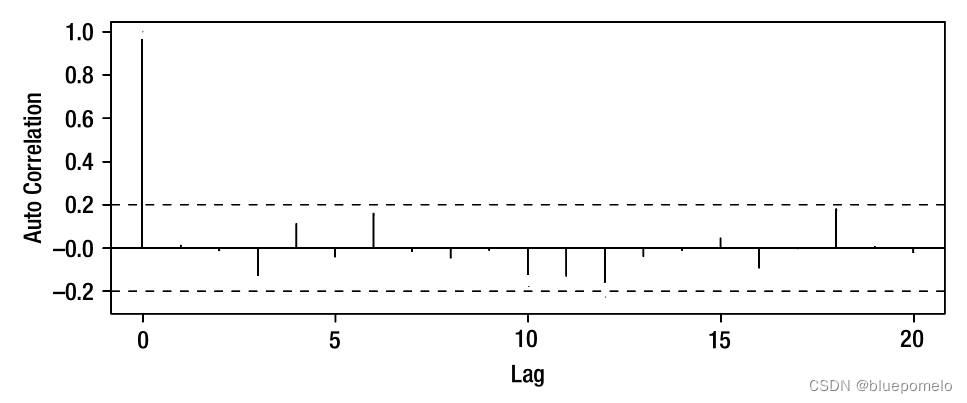
看自相关函数图，当lag=0（时间间隔为0）的时候，自相关性是1，这是自然的，每个值自己跟自己的相关性是1。对于其它的lag值，相关性小到可以忽略不计了。这是因为，所有的值都来自(抽样自）相同的独立的正态分布。独立的随机变量之间的相关性是0，也就是它们是不相关的。白噪声中每个值与不同时间间隔(time lag)的值之间是不相关的，而这也反映在自相关图上。

白噪声时间序列的可预测性：过去的时间序列值（历史数据）是否有助于预测下一时刻的时间序列值？答案是某种程度上是有帮助的。历史数据可以用来估计正态分布的方差。这使我们能够得出一些结论，比如时间序列下一时刻的值大于或小于某个值的可能性。

总的来说，在白噪声序列中，序列中每个点的值的方差就是白噪声值服从的正态分布的方差。这种正态分布具有特定均值和方差，不会随着时间改变。因此，白噪声序列是具有恒定均值和方差的，由不相关的随机变量组成的序列。