从0开始的秋招刷题路，记录下所刷每道题的题解，帮助自己回顾总结

801. 使序列递增的最小交换次数

我们有两个长度相等且不为空的整型数组 nums1 和 nums2 。在一次操作中，我们可以交换 nums1[i] 和 nums2[i]的元素。

例如，如果 nums1 = [1,2,3,8] ， nums2 =[5,6,7,4] ，你可以交换 i = 3 处的元素，得到 nums1 =[1,2,3,4] 和 nums2 =[5,6,7,8] 。
返回 使 nums1 和 nums2 严格递增 所需操作的最小次数 。

数组 arr 严格递增 且 arr[0] < arr[1] < arr[2] < … < arr[arr.length - 1] 。

注意：

用例保证可以实现操作。

示例 1:
输入: nums1 = [1,3,5,4], nums2 = [1,2,3,7]
输出: 1
解释:
交换 A[3] 和 B[3] 后，两个数组如下:
A = [1, 3, 5, 7] ， B = [1, 2, 3, 4]
两个数组均为严格递增的。

示例 2:
输入: nums1 = [0,3,5,8,9], nums2 = [2,1,4,6,9]
输出: 1

提示:
2 <= nums1.length <= $10^5$
nums2.length == nums1.length
0 <= nums1[i], nums2[i] <= $2\ast 10^5$

方法一：动态规划
由于我们每次交换数字只需要和前一个数字进行比较，所以可以采用动态规划来解决。

条件①：nums1[i] > nums1[i - 1] && nums2[i] > nums2[i - 1]
条件②：nums1[i] > nums2[i - 1] && nums2[i] > nums1[i - 1]

若满足条件① && 满足条件②

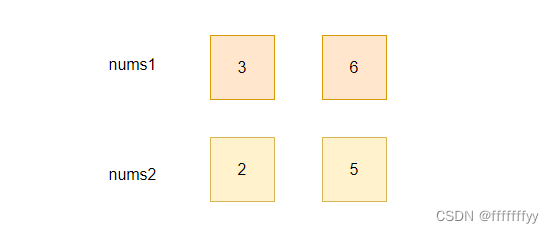
交换和不交换都不影响递增，我们选择上一次的最小值，所以有

dp[i][0] = Math.min(dp[i - 1][0], dp[i - 1][1]);
dp[i][1] = Math.min(dp[i - 1][0], dp[i - 1][1]) + 1;

若满足条件① && 不满足条件②

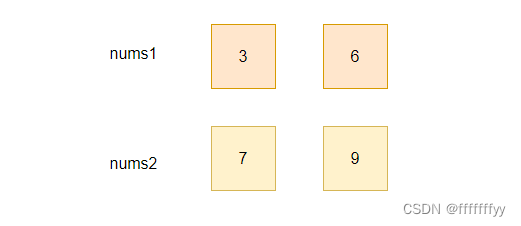
若6和9交换则必须3和7也交换，才能保证递增，所以有

dp[i][0] = dp[i - 1][0]; 都不交换
dp[i][1] = dp[i - 1][1] + 1; 都交换

若不满足条件①

由于题中要求一定可以成功 如图，我们可以选择交换6和2或者3和7，所以有

dp[i][0] = dp[i - 1][1]; 上一次交换
dp[i][1] = dp[i - 1][0] + 1; 本次交换

public int minSwap(int[] nums1, int[] nums2) {
    int n = nums1.length;
    int[][] dp = new int[n][2];
    dp[0][0] = 0;
    dp[0][1] = 1;
    for (int i = 1; i < n; i++) {
        if (nums1[i] > nums1[i - 1] && nums2[i] > nums2[i - 1]) {
            //当前数字大于前一个数字
            if (nums1[i] > nums2[i - 1] && nums2[i] > nums1[i - 1]) {
                //当前数字大于另一个数组的前一个数字

                //前一个交换不交换都无所谓
                dp[i][0] = Math.min(dp[i - 1][0], dp[i - 1][1]);
                //交换 + 1
                dp[i][1] = Math.min(dp[i - 1][0], dp[i - 1][1]) + 1;
            } else {
                //当前数字不大于另一个数组的前一个数字

                //当前数字不交换，上一个也不能交换
                dp[i][0] = dp[i - 1][0];
                //当前数字交换，上一个也必须交换
                dp[i][1] = dp[i - 1][1] + 1;
            }
        } else {
            //当前数字不大于前一个数字

            //本次不交换 则上一次交换
            dp[i][0] = dp[i - 1][1];
            //本次交换 则上一次不交换
            dp[i][1] = dp[i - 1][0] + 1;
        }
    }
    return Math.min(dp[n - 1][0], dp[n - 1][1]);
}