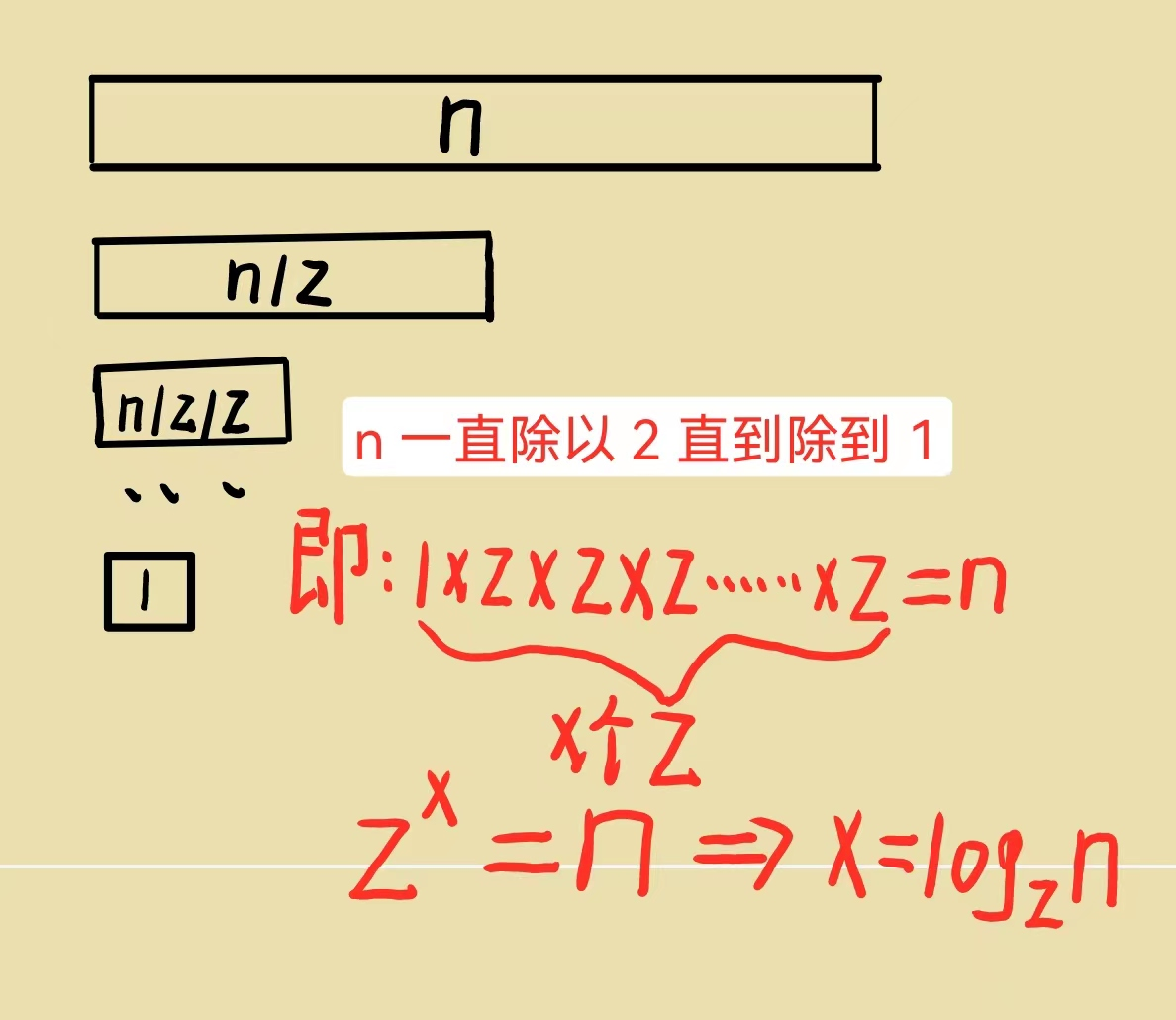
详细思路以及发布视频版,大家可以去观看,这里是对应的文字版,内容相差不多。
B题:快递需求分析问题
B题的问题难度不大,难点就在于后几问的模型求解。问题多、模型多、冗杂,就是B题的特点。
难度 A>B>C
选题 B>C>A
给出数据 数据预处理(异常值、缺失值)
问题多、结果半开放式
评价+预测+优化
(数据文件介绍)附件1、附件2、附件3为国内某快递公司记录的部分城市之间的快递运输数据,包括发货日期、发货城市以及收货城市(城市名已用字母代替(脱敏),剔除了6月、11月、12月(可行性)的数据)。
数据预处理(缺失值0不是缺失值,异常值)

问题一:附件1为该快递公司记录的2018年4月19日—2019年4月17日的站点城市之间(发货城市-收货城市)的快递运输数据,请从收货量、发货量、快递数量增长/减少趋势、相关性等(最大收货量,最大发货量)多角度考虑,建立数学模型,对各站点城市(样本)的重要程度进行综合排序,并给出重要程度排名前5的站点城市名称,将结果填入表1。
问题一,简化而言就是选择指标。建立综合评价模型。在模型建立之前我们还要进行数据预处理,对于B题,题目给出了数据文件,我们还需要考虑缺失值、异常值问题。对于指标的选取,题目暗示我们可以从收货量、发货量、快递数量增长/减少趋势、相关性等。或者还可以从其他的角度出发,例如大收货量,最大发货量等等。
对于收货量的计算问题,我们可以使用wps的筛选功能,将同一城市作为发后城市情况列举出来,在进行分析即可。或者大家可以利用matlab、python等进行几次for循环,将结果相同的城市计算发货量等等。
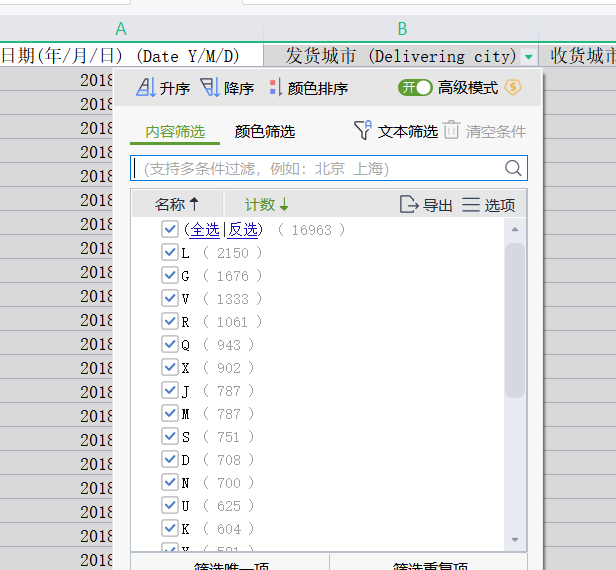
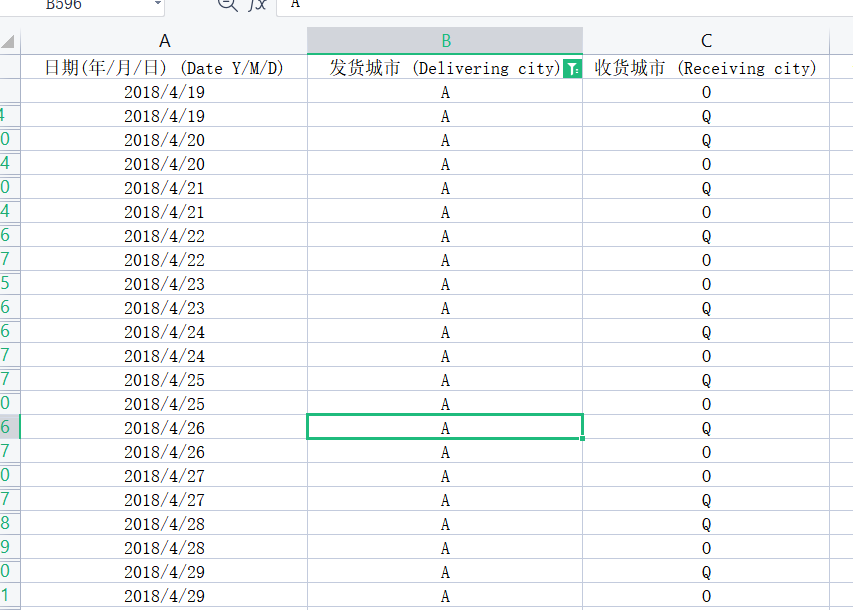
建立综合评价模型。对于模型的选取,我们有很多的选项,例如主成分、秩和比、理想解法等客观综合评价方法。这个问题属于综合评价是一个开放式的,但是它让我们具体的结果填入这个表格。结果排名前五名可能有一个范围,所以对于这个题来说,它的综合评价是一个结果半开放式。只要选了一个综合评价模型,代入代码包就可以了。

问题二、请利用附件1数据,建立数学模型,预测2019年4月18日和2019年4月19日各“发货-收货”站点城市之间快递运输数量,(以及当日所有“发货-收货”站点城市之间的总快递运输数量),并在表2中填入指定的站点城市之间的快递运输数量,以及当日所有“发货-收货”站点城市之间的总快递运输数量。
对于问题二,本质是一个简单的预测模型。难度不在于预测模型的选取,而是数据量很多,需要我们反复进行多次预测。对于预测模型的选择,我们有很多很多合适选项,如下图所示。

例如当前正火的LSTM模型,基于其长期记忆功能,能很好的区别出长期趋势和季节趋势。
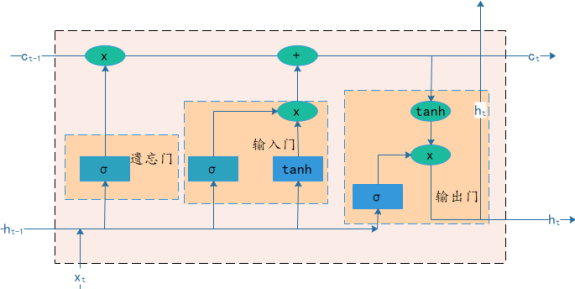
该模型也是我经常使用的预测模型,因此为了方便,该模型的代码已经改为修改最初输入数据,再根据数据调整几处参数即可运行出结果(要修改参数的位置都有标注)(放在后续的分享中供大家参考使用)
对于问题二,这么多的预测结果,如果队伍感觉时间宽裕,我们可以一个一个的进行预测。其实还有种比较快的方式,就是填充,我们预测两三次,对结果的区间大致有了了解。剩下的结果,我们可以进行编写,切记这种做法数据黑箱做法,不能放于论文描述,论文中还是说,我们建立了XXXXX预测模型,得到了XXXX结果。这种方法只是加快模型的求解。
问题三、附件2为该快递公司记录的2020年4月28日—2023年4月27日的快递运输数量。由于受到突发事件影响,部分城市之间快递线路无法正常运输,导致站点城市之间无法正常发货或收货(无数据表示无法正常收发货,0表示无发货需求)。请利用附件2数据,建立数学模型,预测2023年4月28日和2023年4月29日可正常“发货-收货”的站点城市对(发货城市-收货城市),并判断表3中指定的站点城市对是否能正常发货,如果能正常发货,给出对应的快递运输数量,并将结果填入表3。
问题三,依旧是一个预测模型,它的难度在于出现了无法正常发货的情况,这种情况我们可以近似的认为是一种异常值处理,对于判断表3中指定的站点城市对是否能正常发货,我们可以理解为异常值的预测。因为,异常值的预测问题相关文献,代码、模型就很多了。对于问题三的模型我们依旧可以与问题二相同,选择基础的预测模型,也可以选择高级的更加适用于异常值的预测模型。这里稍后会给大家补充一下相关资料。对于快递运输数量的预测,就可以与问题二建立的预测模型一样即可。对于是否能正常发货就可以单独在建立一个模型,或者沿用问题二的模型都是可以的。
问题4

备注:为了方便计算,不对快递重量和大小进行区分,假设每件快递的重量为单位1。仅考虑运输成本,不考虑中转等其它成本。
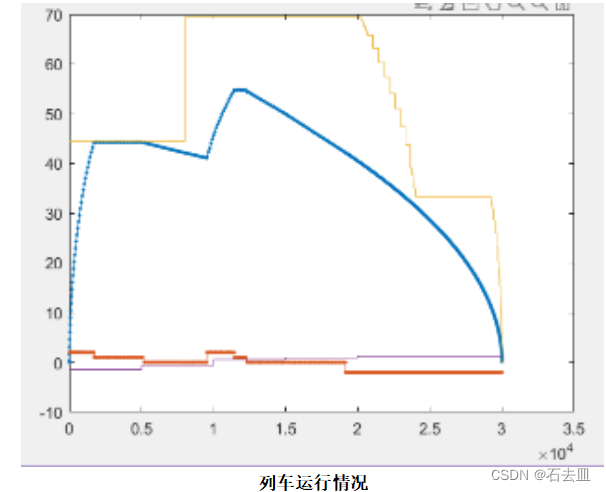
问题四,就是一个变种TSP问题,类似于2003年露天矿的开采、交巡警服务平台的设置与调度的问题设置类似。大家可以参考这两个问题的决策变量设置方式。稍后,我也将对这两场比赛的资料进行收集。我目前的初步想法就是,以最低运输成本为目标函数,题干的各种条件作为约束条件,Xij为决策变量,表示第I个城市到第J个城市的运货量。大家可以参考一下。
对于优化模型的求解,熟悉优化的人建立模型进行求解,即可。对于小白来讲,这一问的难度难如登天。所以,这就涉及到我十课时保奖的理论,合适的模型+高级算法+合理的结果 就可以获奖。什么是合理的结果,这就是针对很多小白,知道了一些模型,但是无法进行求解。我们缺一个结果。结果的获取,大家可以去网上查找购买,也可以进行数值模拟,或者最简单的就是编,编出一个合理的结果即可。前提是,合理!!通常评委很难看出一个结果是否是捏造的,因此,对于无法对模型进行求解的情况,我们可以选择进行捏造合理结果即可。
问题五、通常情况下,快递需求由两部分组成,一部分为固定需求,这部分需求来源于日常必要的网购消费(一般不能简单的认定为快递需求历史数据的最小值,通常小于需求的最小值);另一部分为非固定需求,这部分需求通常有较大波动,受时间等因素的影响较大。假设在同一季度中,同一“发货-收货”站点城市对的固定需求为一确定常数(以下简称为固定需求常数);同一“发货-收货”站点城市对的非固定需求服从某概率分布(该分布的均值和标准差分别称为非固定需求均值、非固定需求标准差)。请利用附件2中的数据,不考虑已剔除数据、无发货需求数据、无法正常发货数据,解决以下问题。
(1) 建立数学模型,按季度估计固定需求常数,并验证其准确性。将指定季度、指定“发货-收货”站点城市对的固定需求常数,以及当季度所有“发货-收货”城市对的固定需求常数总和,填入表5。
(2) 给出非固定需求概率分布估计方法,并将指定季度、指定“发货-收货”站点城市对的非固定需求均值、标准差,以及当季度所有“发货-收货”城市对的非固定需求均值总和、非固定需求标准差总和,填入表5。
对于问题五,目前我还没有找到合适的模型归类,只能认为是一个常规的数据计算类题目。稍后有更深的理解,会及时给大家更新。
最后,预祝大家比赛顺利,假期愉快。!!!!11