模运算

分数求模

# 一个例子
1/2 mod 23
n ≡ 1/2 mod 23
2n ≡ 1 mod 23
# 也就是求2的逆元了
n = 12

负数求模

# 一个例子	x mod y ≡ x-y* |⎣x/y⎦|
# 后面的是 x/y并且向下取整
-73 mod 23 ≡ -73 - 23 * ⎣-73/23⎦
					 = -73 - 23 * ⎣-3.17⎦
					 = -73 - 23 * -4
					 = -73 + 92
					 = 19

gcd最大公约数

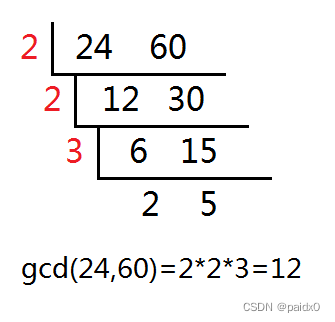
逆元

# 辗转相除
除数作为被除数、余数作为除数
一直循环除，直到除数为 0
逆元 = 余数不为0的商相乘 + 除数为0的被除数(也就是gcd)

分组密码

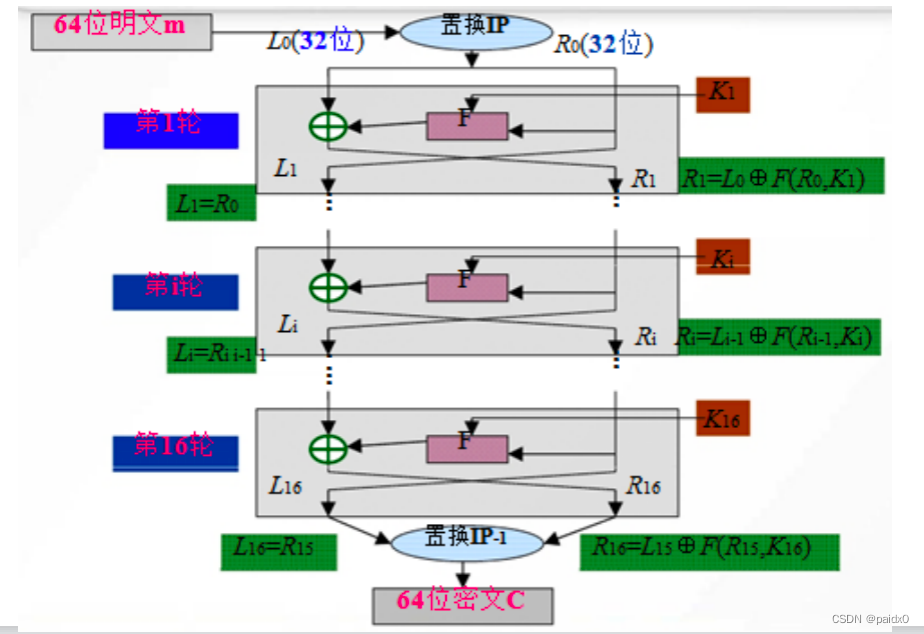
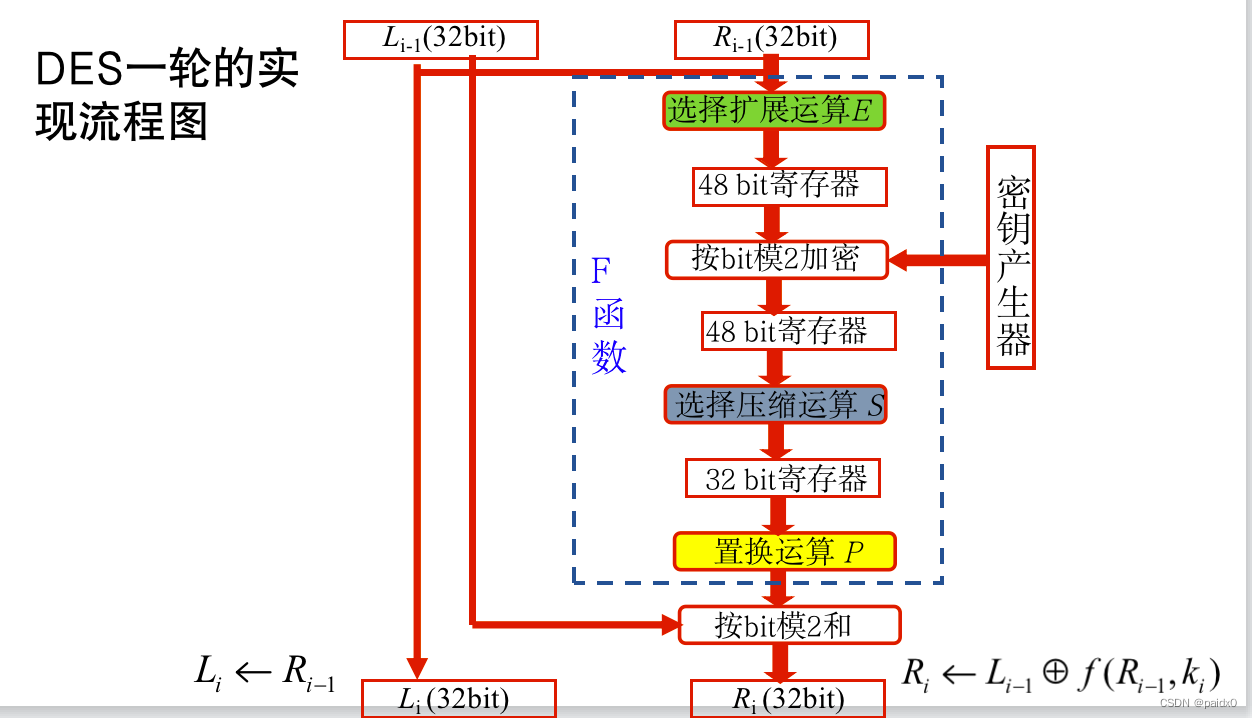
DES加密

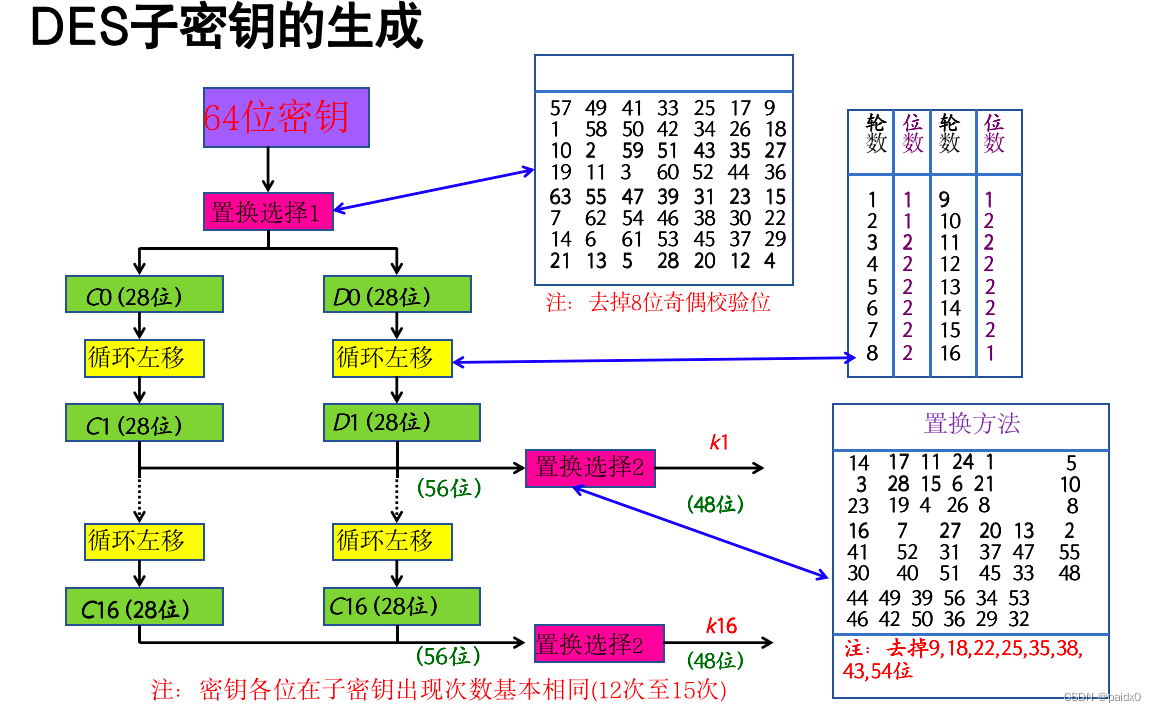
# 分组长度64位，64位秘钥（8位校验位）,16轮迭代，每轮子密钥48位
# Feistel网络

# 加密
Li = Ri-1
Ri = Li-1⨁F(ki,Ri-1)
# 解密
Ri-1 = Li
Li-1 = Ri⨁F(ki,Li)

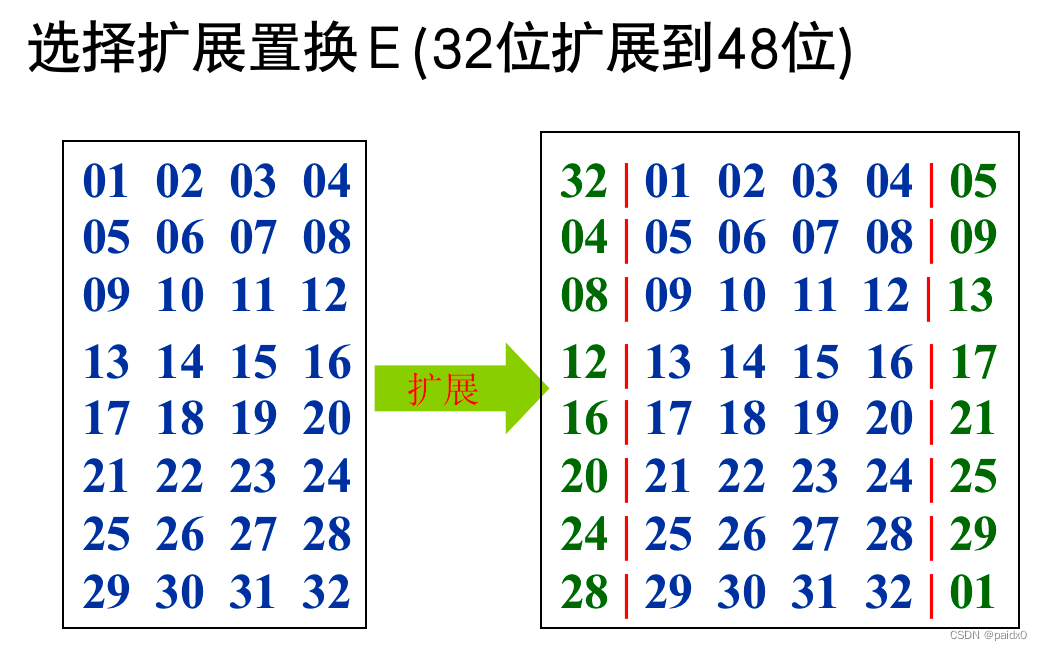
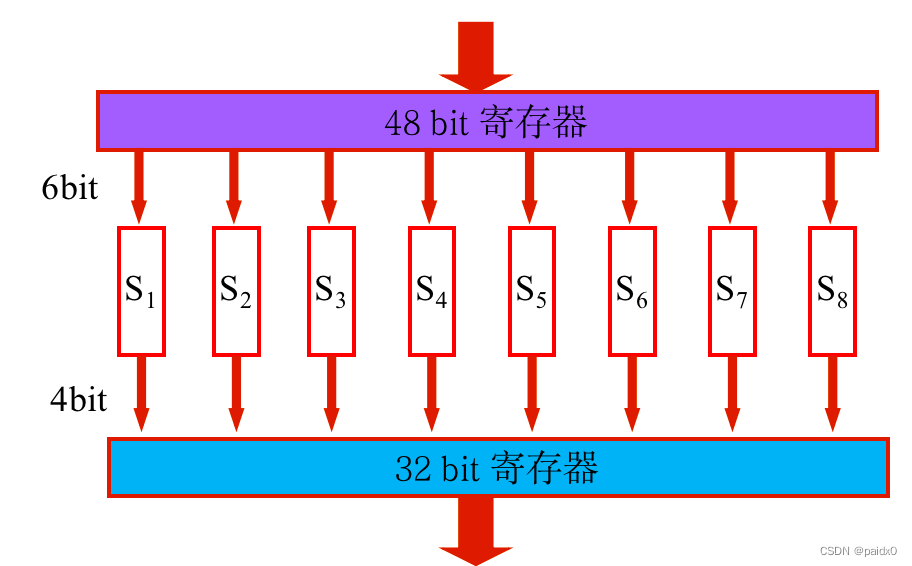
# S盒 4行16列，每行都是打乱顺序的0~15，48位8组，每组6位
# 100011，首尾代表行11(3)，中间代表列0001(1)，所以置换成第3行1列的数字，也就是6位压缩成4位

AES加密

........

操作模式

• ECB最快最简单，安全性最弱，通常加密随机数据

• CBC适合文件、软件加密，少量错误不会造成同步失败

• CFB加密字符序列，具有同步恢复

• OFB极易出错的环境使用，需要严格高速的同步机制

ECB电子密码本

简单，主要内容较短且随机的报文传递
加密独立分组，可以并行
单个分组的比特错误不会传播其他分组
# 相同明文或秘钥得到相同的密文，明文中重复的内容在密文体现出来，容易被统计

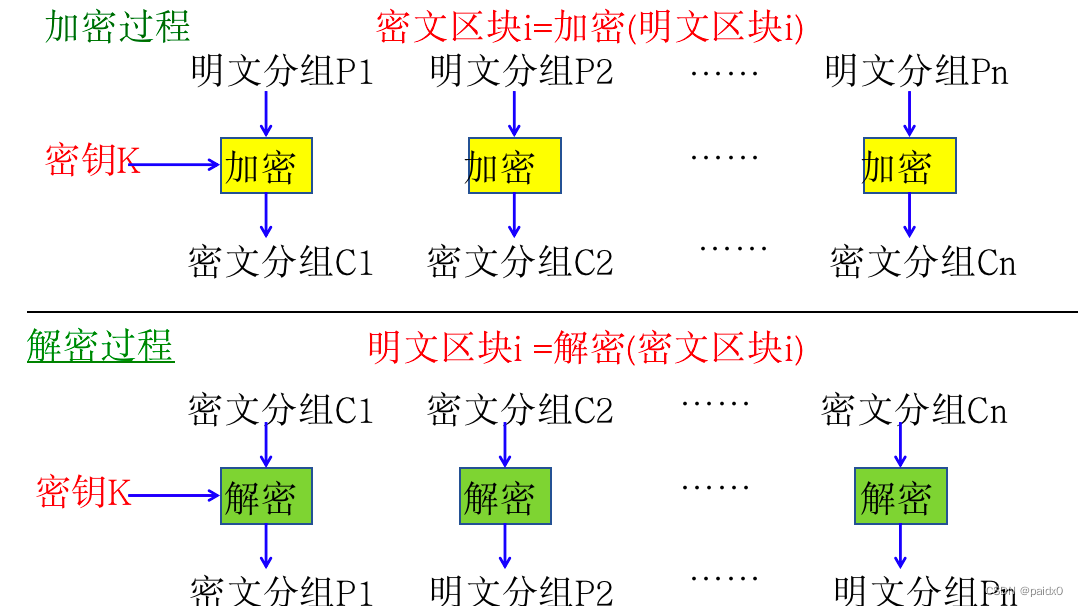
CBC分组链接

反馈机制，密文不仅依赖明文，还依赖前面的密文分组
正确解密需要确保前面的每个密文分组都是正确的
密文分组中的比特错误传播影响到本组和下一组的解密

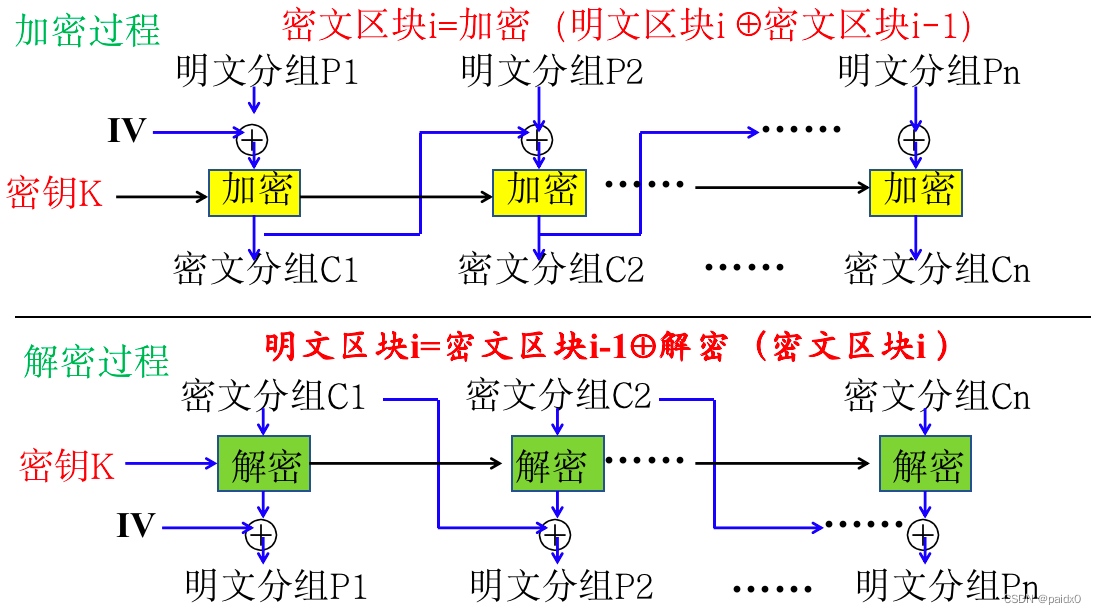
CFB密码反馈

对信道错误较敏感且造成错误传播
数据加解密的速率降低，其数据率不会太高
主要适用数据库加密、无线电通信或密文信号容易丢失出错的环境

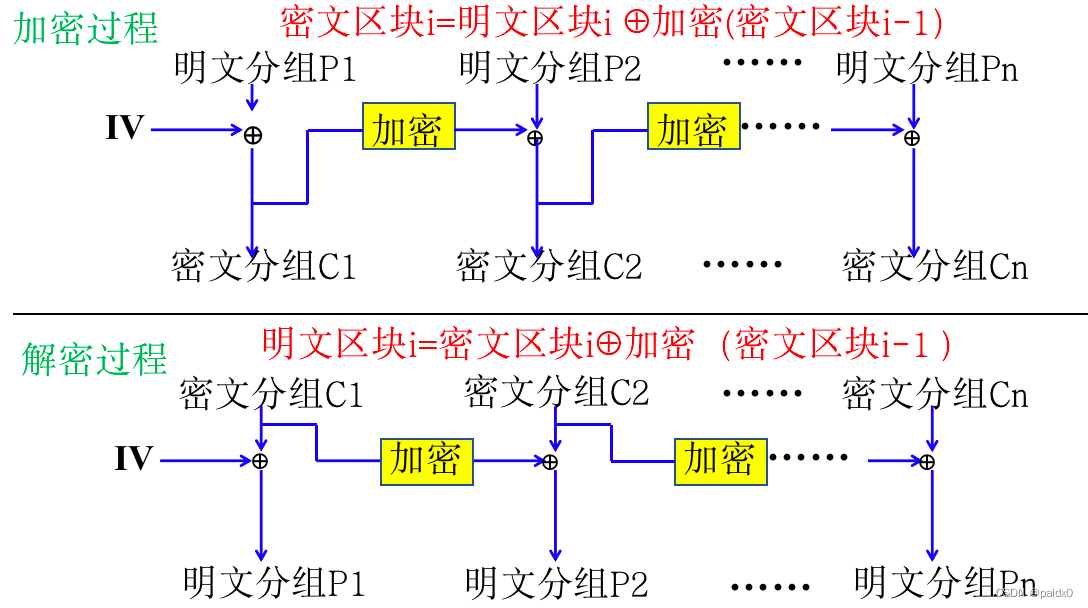
OFB输出反馈

克服错误传播带来的问题，但对密文被篡改难于检测
不具有自同步，需要保持严格的同步

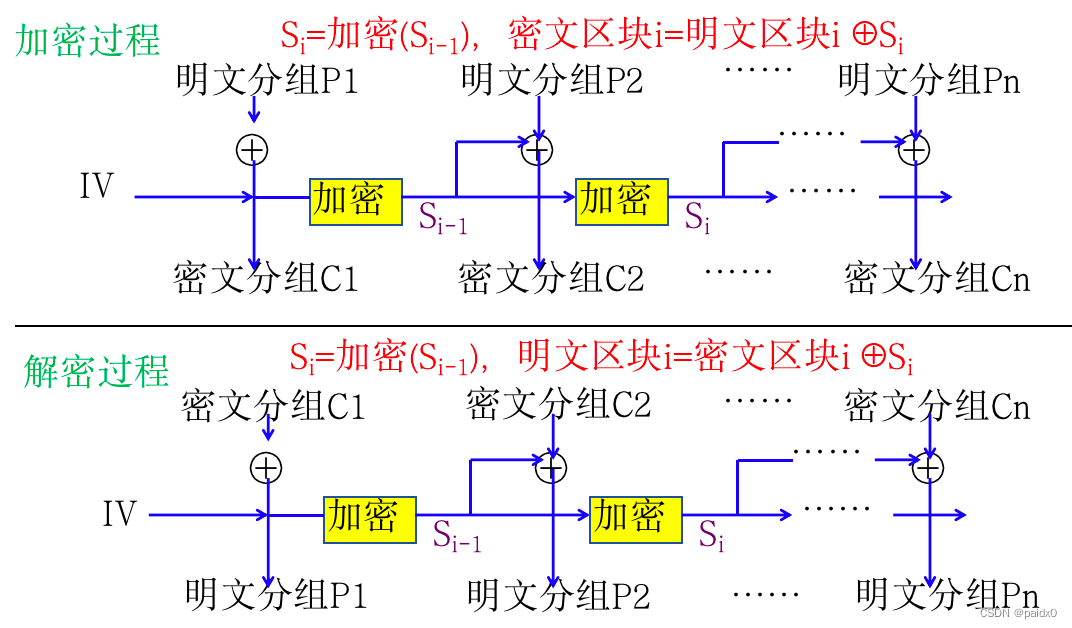
序列密码

A5-1算法

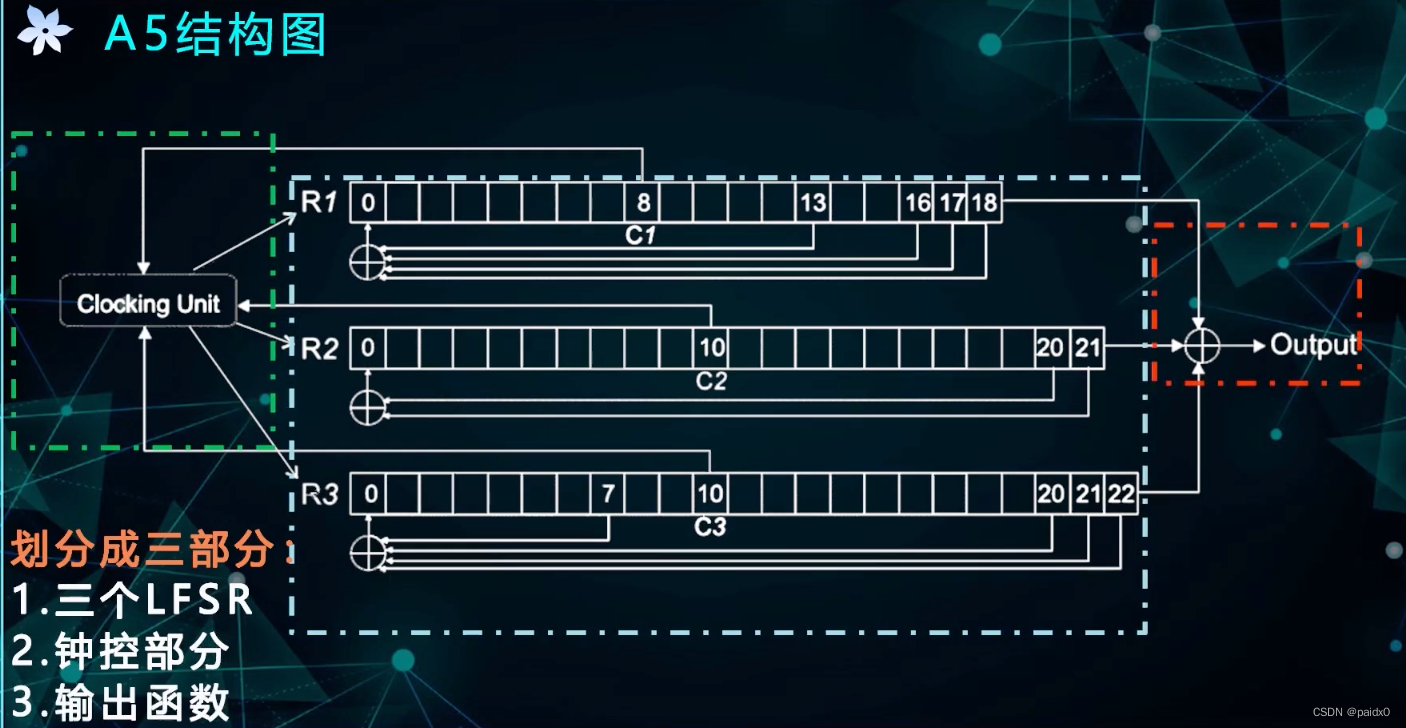
# 三个反馈序列LFSR，长度19、22、23

a1= [18]⨁[17]⨁[16]⨁[13]
a2= [21]⨁[20]
a3= [22]⨁[21]⨁[20]⨁[7]

x,y,z = LFSR1[8],LFSR2[10],LFSR3[10]
# (x,y,z)作为忠控函数的输入
# 钟控方式：择多原则，占比多的被驱动，保证至少两个LFSR是被驱动的
010，0更多，所以LFSR1和LFSR3被驱动
101，1更多，所以LFSR1和LFSR3被驱动

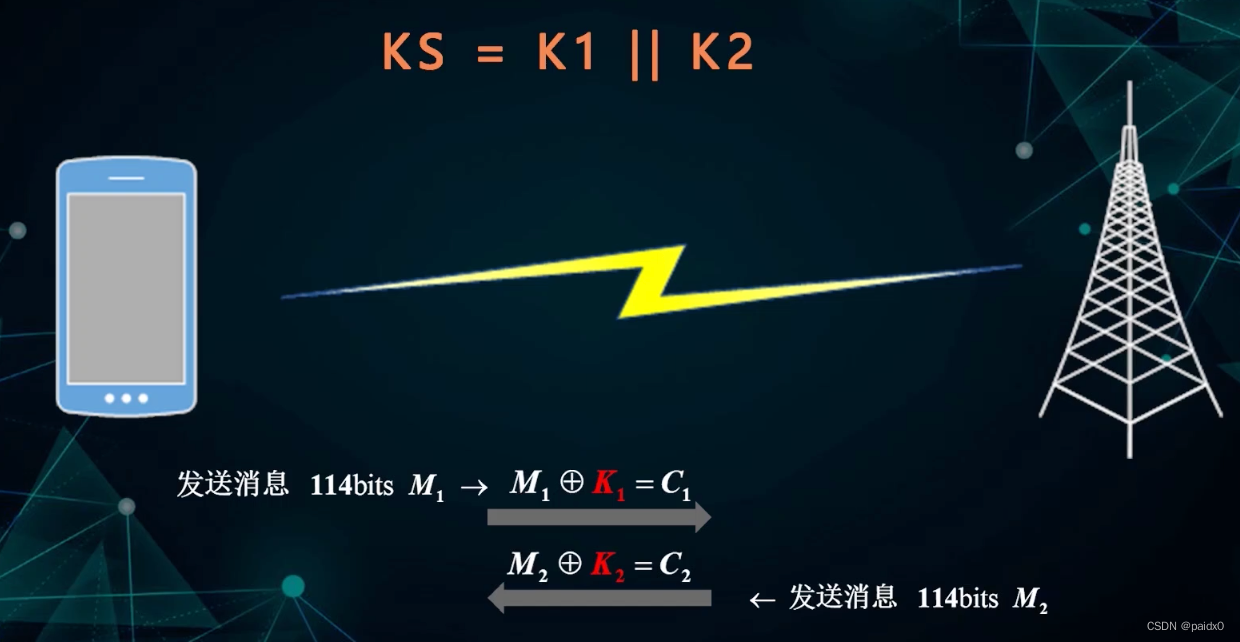
将得到的 228 bit的密钥流ks分组 k1和k2
手机用 k1对要发送的信息 M加密，基站用 K1解密
基站用 k2对要发送的信息 M加密，手机用 k2解密

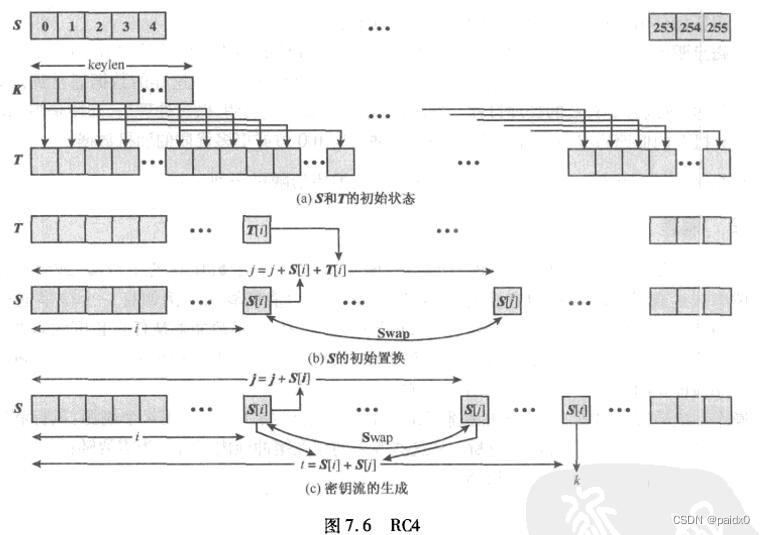
RC4算法

# 初始状态向量S，256字节，0~255
# 初始秘钥T，不足256字节长度，轮转补充
# T表对S表初始置换
j = 0;
for (i = 0 ; i < 256 ; i++){
　 j = (j + S[i] + T[i]) mod 256;
　 swap(S[i] , S[j]);
}
# 密钥流生成
i=0;
j=0;
while(datalength--){
　　i = (i + 1) mod 256;
   j = (j + S[i]) mod 256;
 　swap(S[i] , S[j]);
 　t = (S[i] + S[j]) mod 256;
 　k = S[t];
   # 加密方法
   c[] = data[] ⨁ k
}

Hash函数

Md5算法

迭代模型
输入任意长度数据块，每一次迭代处理512bit的消息分组，最终输出散列值128bit
# 所以必须是512bit的整数倍
消息 + 填充(100...00，一个1， 若干个0，必须被 填充1~512bit) + 消息长度预留空间(64bit)
# 4个初始化缓冲区，用于计算消息摘要的128位缓冲区
A: 01 23 45 67
B: 89 ab cd ef
C: fe dc ba 98
D: 76 54 32 10
。。。

SHA-1算法

# 填充方法和MD5相同
# 5个初始缓冲区
A: 67 45 23 01
B: ef cd ab 89
C: 98 ba dc fe
D: 10 32 54 76
E: c3 d2 e1 f0 
。。。

消息认证

只对消息完整性认证，但没有对消息来源认证，可以被替换

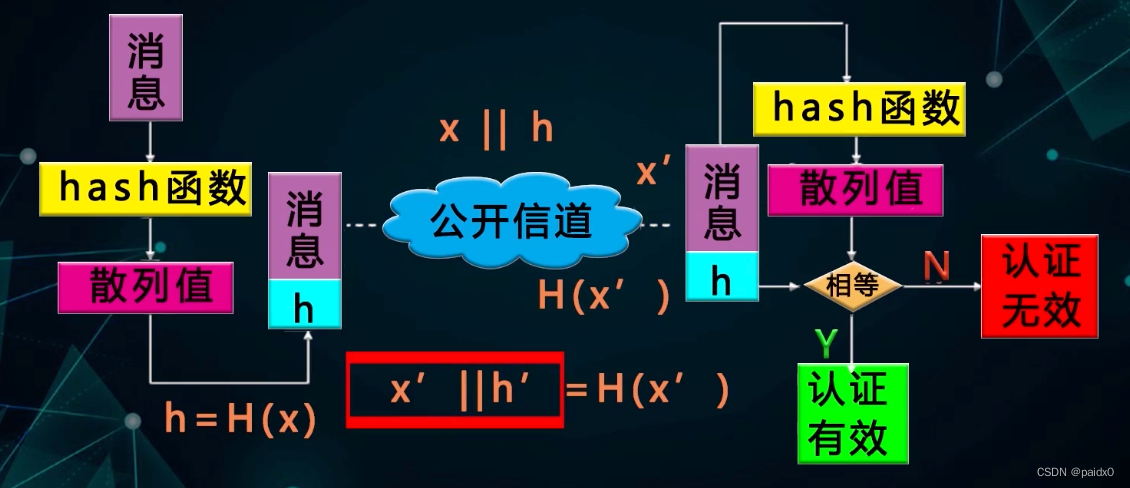
消息认证码：共享秘钥 k

秘钥参与，要篡改必须知道秘钥k

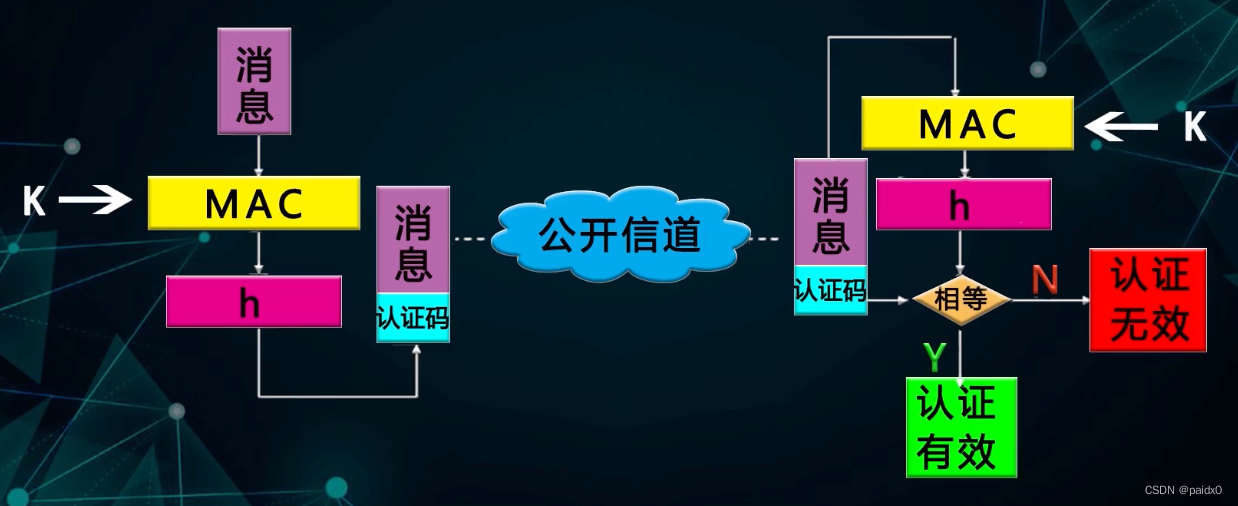
CBC-MAC
HMAC-MD5
HMAC-SHA1

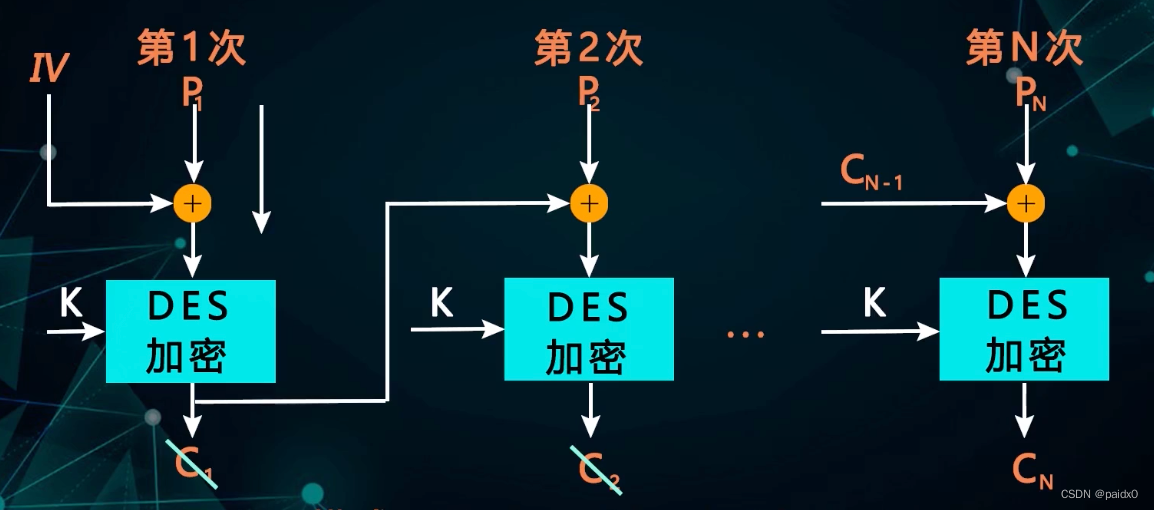
CBC-MAC：用相同的Pi、相同的方法、相同的秘钥计算Cn，然后与接收到的Cn比较实现消息认证

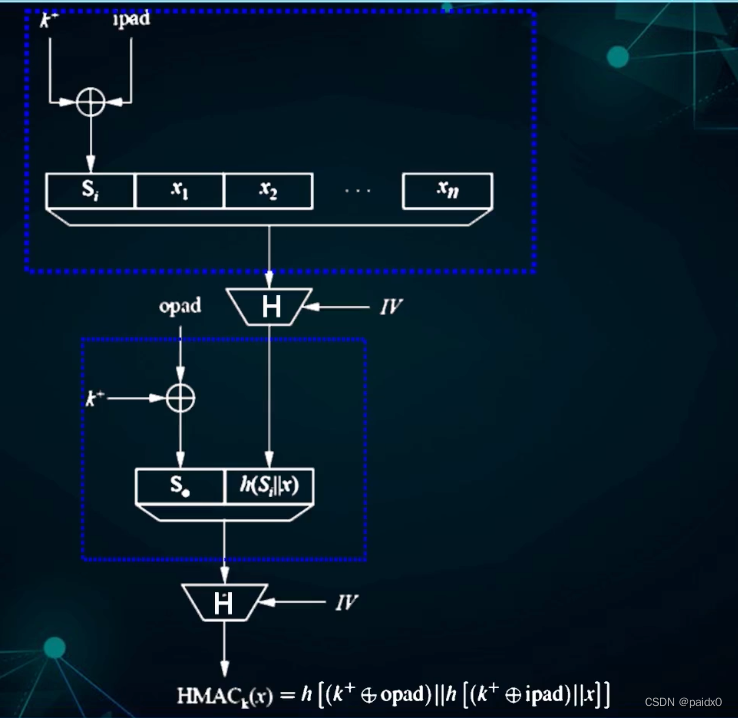
HMAC：秘钥 K长度填充0，使长度为b比特
Si = k ⨁ ipad ，ipad是一个长度b比特的固定比特串，将 00110110重复b/8次后得到的比特串
作为Hash函数H的输入，得到 t 比特的输出 h
So = k ⨁ opad , opad是一个长度b比特的固定比特串，将 01011010重复b/8次后得到的比特串
和h连接作为第二个 H的输入，得到 t比特的输出，即消息的认证码

数字信封

# A 产生一个128bit会话秘钥k
Ek(M,sigA(H(M)))，PEB(k) 发送给B，称为数字信封

B 用私钥解密 PEB(k)得到会话秘钥 k，利用 k对Ek(M,sigA(H(M)))解密，得到 M和 sigA(H(M))，用A的公钥解密 sigA得到H(M)，计算M的hash,对比 H(M)是否相等

公钥密码

背包公钥算法

b1v1 + b2v2 + b3v3 + ... = c
# b = 1或0，1代表存在这个物品，0代表不存在这个物品
# c 指背包容量
# 总能找到一个子集合作为背包向量的解

**超值增背包问题 **

V = (v1,v2,v3,v4...vn)，是一个背包向量
# 满足下一个Vi > 前面i-1个向量之和，这样的序列称为超递增序列
# 比如 1、2、4...2^n

可以发现，超递增序列要找出一个子集合的解还是很容易的。

只需要从后往前找，如果小于 c，那么 bi就置为1，更新 c的值，继续向前找直到 c更新到0，否则就不是存在这样的子集合解。

超值增背包问题找到一个子集合的解很容易，但是求解一般的背包问题是困难的。
加密采用一般背包加密是难以求解的，求解的过程如果可以把一般背包问题转变成超递增背包问题，那就很容易求解。

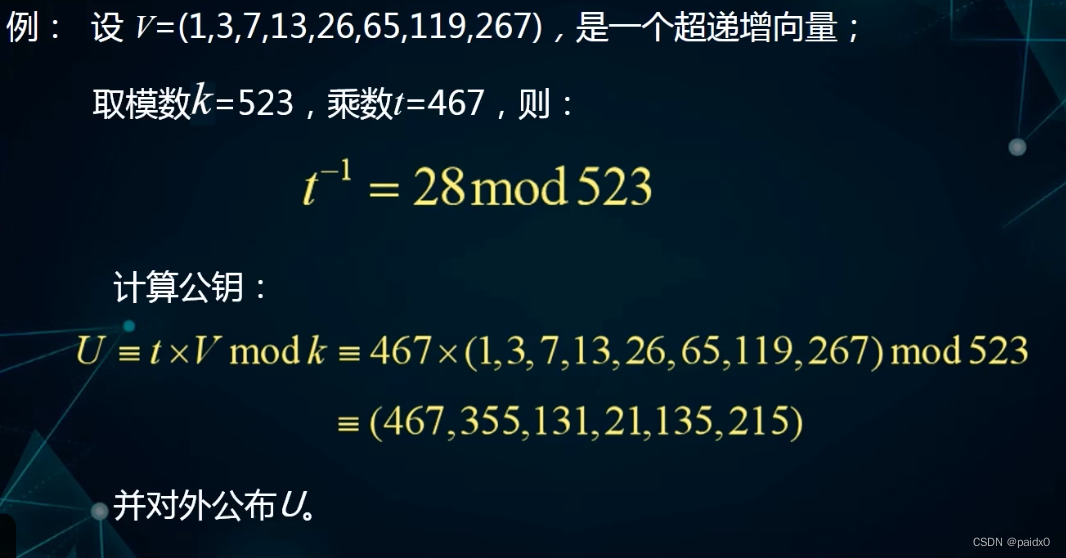
1、产生一个超递增向量 V
2、超递增向量 V转化成非超递增向量 U
3、公钥就是 U
4、私钥就是转化因子 t 和 k

# gcd(t,k)=1  互素，保证t在模k下的乘法逆元t^-1存在
# U = tV mod k = t(v1,v2,v3,v4...vn) mod k

# 加密过程前需要先将明文长度按照 U 的长度划分，(b1,b2,b3...bn)
# 计算分组向量内积，BU = b1u1 + b2u2 +b3u3 +...+ bnun
得到密文c

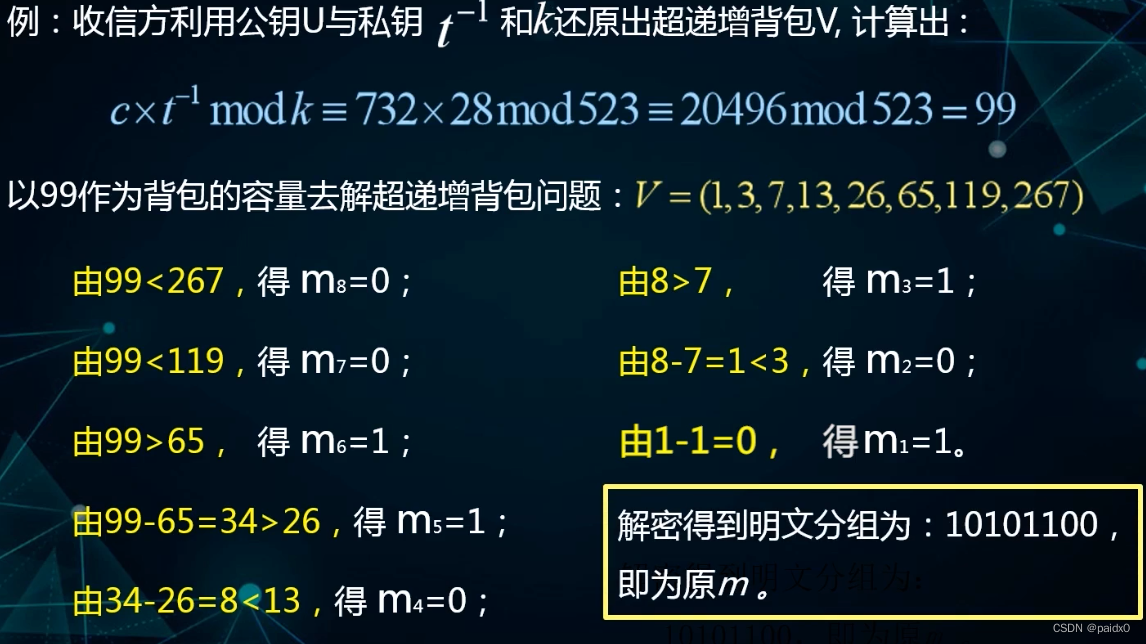
# 利用 k 和 t^-1 还原出超递增背包向量 V
c = BU
V = t^-1U mod k 
# 得到背包容量
ct^-1 mod k = BUt^-1 mod k = BtVt^-1 mod k

RSA公钥算法

# 独立选取两个大素数 p 和 q
# n = p * q
# 欧拉函数 𝜑(n) = (p-1)(q-1)
# 随机选取一个e，满足gcd(𝜑(n),e) = 1，1 <e< 𝜑(n)
那么e就存在逆元d
ed = 1 mod 𝜑(n)
# (n,e)作为公钥，d作为私钥

# 加密前先将明文分组长度小于 n的长度
c = m^e mod n

# 解密
m = c^d mod n

# 一个例子
p= 5,q= 11,n= 55,𝜑(n)= 40
取 e= 7，满足 1<e<𝜑(n),且与𝜑(n)互素
得 d= 23
明文m= 531953,分组得m1= 53,m2= 19,m3= 53
# 加密
c1= m^e mod n = 53^7 mod 55 = 37
c2= 19^7 mod 55 = 24
c3= 53^7 mod 55 = 37
# 解密
m1= 37^23 mod 55 = 53
m2= 24^23 mod 55 = 19

Rabin公钥算法

# p=3 mod 4 ,q=3 mod 4, p≠q
# n= p*q
n作为公钥，(p,q)作为私钥

# 加密
c = m^2 mod n

# 解密
m^2 = c mod n
# 等价于
m^2 = c mod p
m^2 = c mod q
# 得到四个方程
m1 = c^[(p+1)/4] mod p
m2 = -c^[(p+1)/4] mod p
m3 = c^[(q+1)/4] mod q
m4 = -c^[(q+1)/4] mod q
# 两两组合根据中国剩余定理求解(m1,m3)、(m1,m4)、(m2,m3)、(m2,m4)
# 得到四个解，是c mod n的平方根，明文就是其中之一  

ElGamal公钥算法

# 已知素数p ，有限域Zp上的一个本原根g ，Zp*上的整数y
y = g^x mod p
x = logg(y) mod p
# 已知 g、x、p 求y 容易
# 已知 g、y、p 求x 困难

(g、y、p)作为公钥，(x)作为私钥

# 加密
# Zp*上随机取一整数k
c1 = g^k mod p
c2 = my^k mod p
# 密文c = (c1,c2)，密文长度扩展为明文长度两倍

# 解密
m = c2(c1^x)^-1 mod p
# c2(c1^x)^-1 = my^k *(g^xk)^-1 = mg^xk * g^-xk = m

# 根据加密算法会发现，每次加密的密文不只是和公钥y有关，还与随机数k有关
# 当k泄露时，可以根据 c2 = my^k mod p 得到明文m
# 当k被重复使用时，可以通过 c2/c2' = m/m'，假如知道m，那么m'就也是已知的了

ECC公钥算法

y² + axy +by = x³ + cx² + dx +e (关于x轴对称)

Abel群，无穷远点作为单位元O

曲线上任意一点P，P⨁O=P

曲线上PQR三点共线，P⨁Q⨁R=O

p(x,y) 的⨁逆元为 -p(x,-y)

P⨁Q⨁R=O，P⨁Q=-R，R(x,y)时，⨁逆元-R(x,-y)

当PQ在一点时，也就是重合时，上面连线交点就不适用了，而是用P点的切线与曲线的交点，R(x,y)时，P⨁Q=-R=(x,-y)

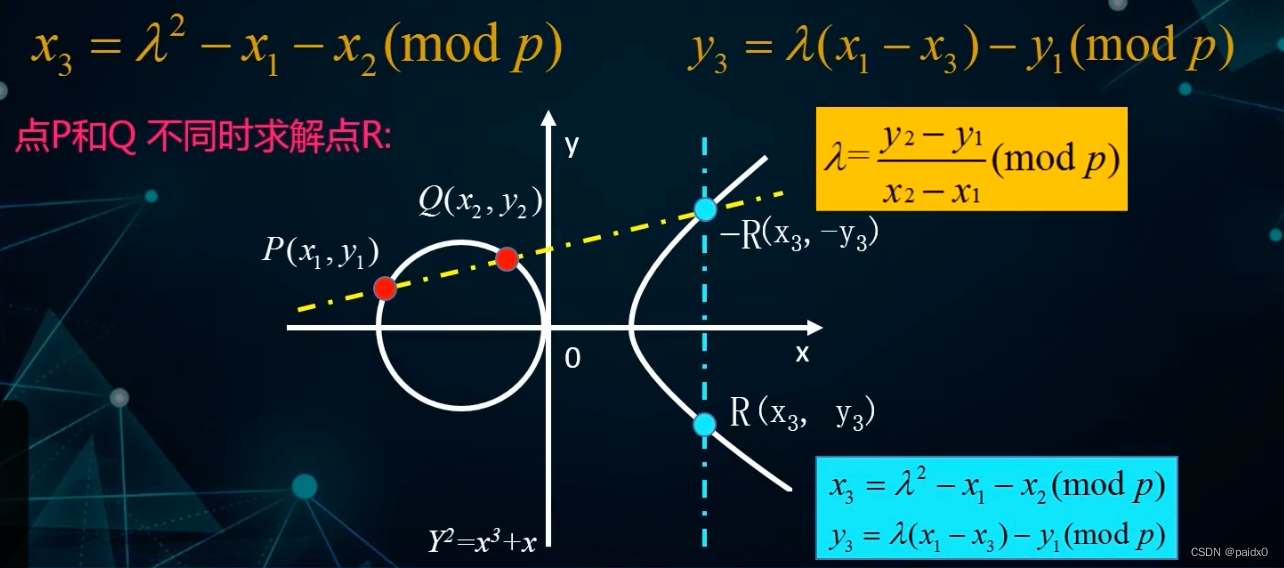
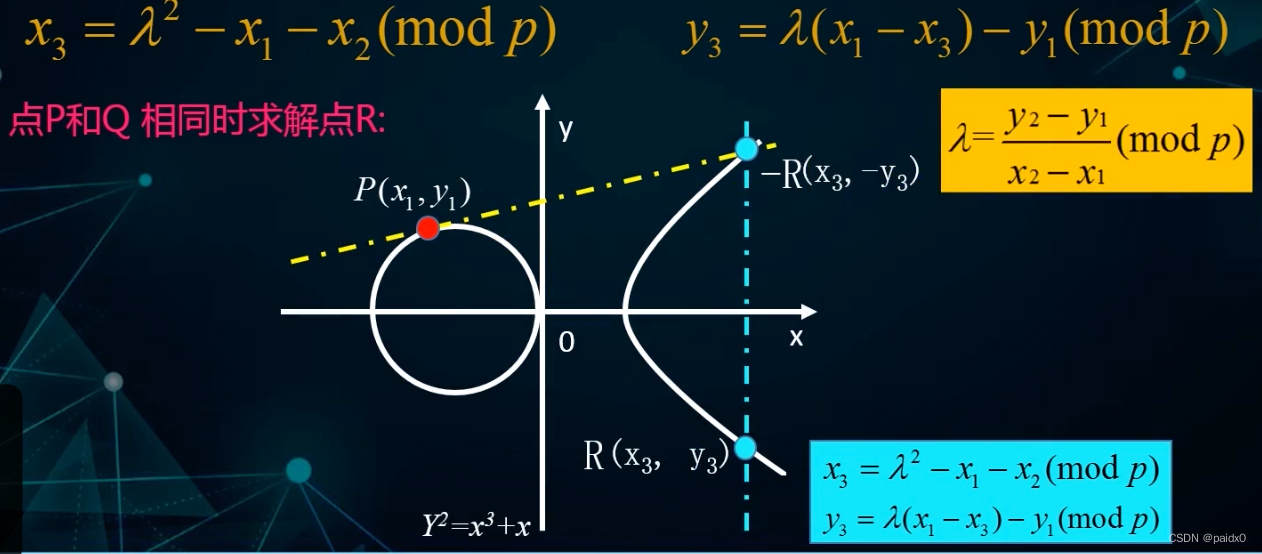
x3 = k^2-x1-x2 mod p，y3 = k(x1-x3)-y1 mod p
# PQ 不同时：k = (y2-y1)/(x2-x1) mod p
# PQ 相同时(切线需要求导)：k = (3x^2 + a)/2y mod p	 

# 椭圆曲线连续的，必须变成离散的点，定义在有限域上，最常见GF(p)
# 不是所有的曲线都适合加密
y^2 = x^3 + ax + b 是最简单的一种加密曲线

Ep(a,b)：y^2 = x^3 + ax + b mod p
0 ≤x、y≤ p，p为质数

Ep(a,b)，基点g属于Ep的Abel群，取x<p，y=xg
(g、y、p)作为公钥，(x)作为私钥
# 加密
# 取随机整数k
c1 = kg，c2 = m⨁ky
c = (c1,c2)
# 解密
m = c2⨁(-xc1)

数字签名

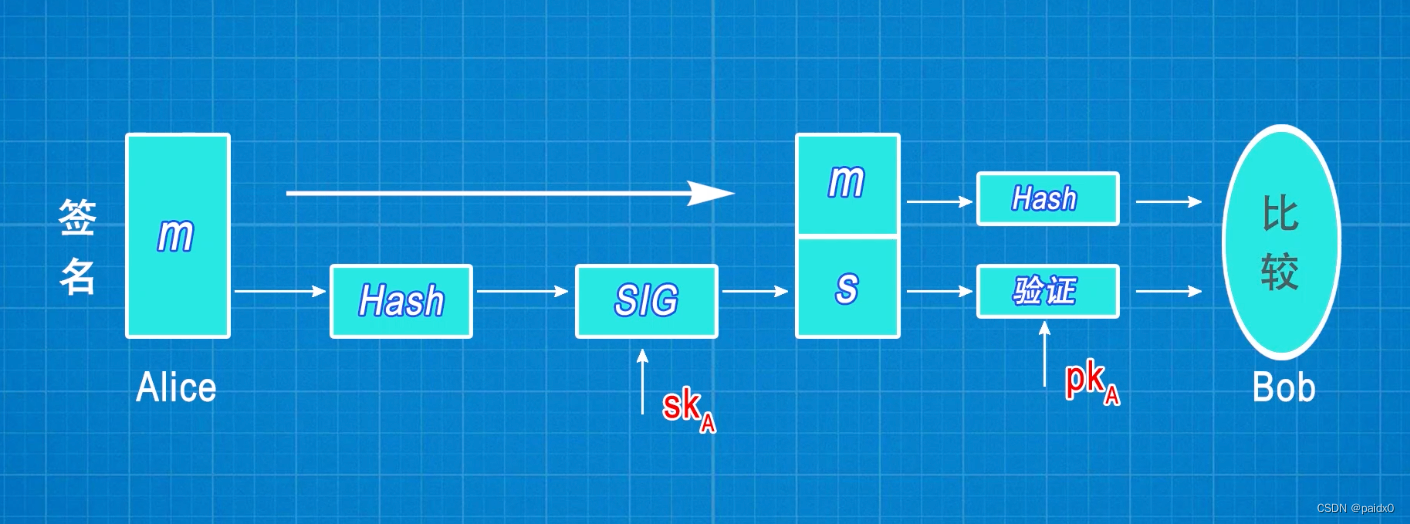
Rsa数字签名

(n,e)作为公钥，(p,q,d)作为私钥
# 私钥加密签名，公钥验证

ElGamal数字签名

(g,y,p)作为公钥，(x)作为私钥
# 随机数k，gcd(k,𝜑(p))=1

# 签名 s = SIG(m,k)=(y,𝒮)
y = g^k mod p
𝒮 = (m - xy)k^-1 mod 𝜑(p)
# 验证 VER(m,y,s)=true <=> 

Schnorr数字签名

p 大素数，q= p-1
g^q = 1 mod p
私钥 x , 1<x<q
公钥 y , y = g^x mod p

# hash函数 H

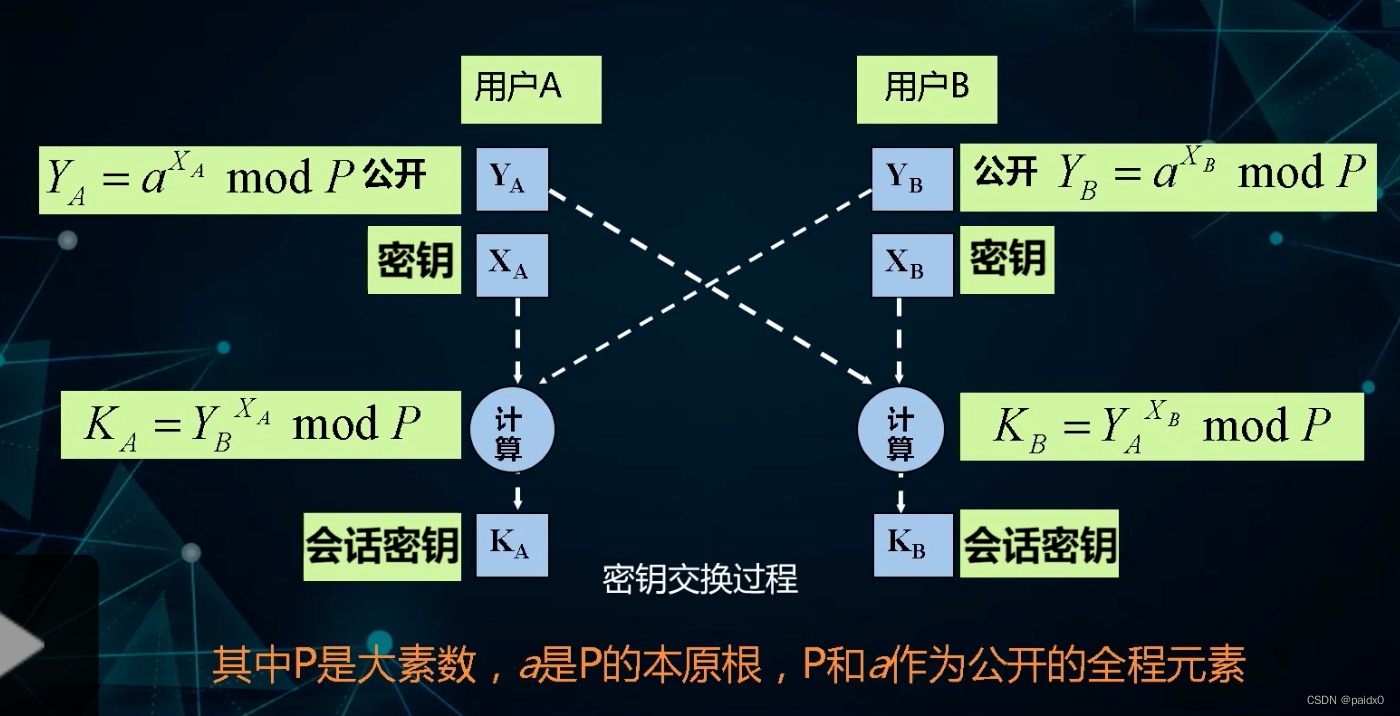
秘钥协商DH算法

# 大素数 p,本原元 a
# 1~ p-1 这些数恰好可以通过a的不同幂次 mod p得到 

Ka = Kb

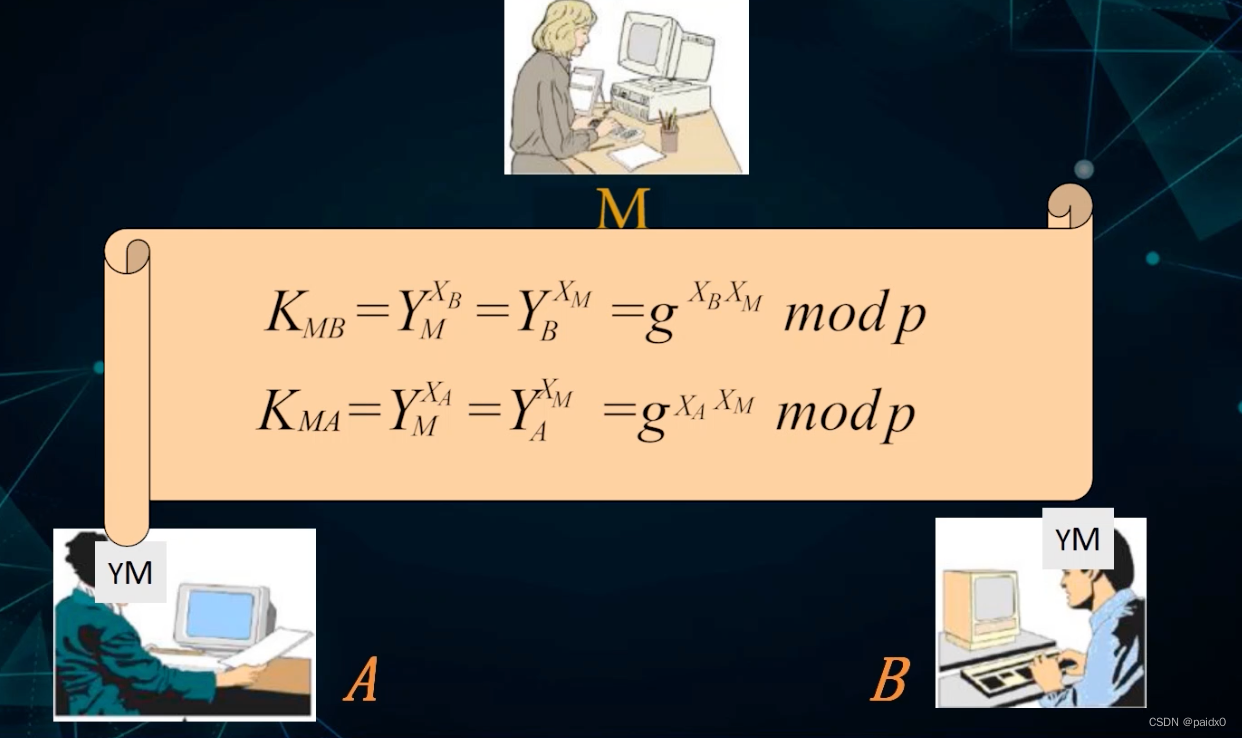
中间人

秘钥共享门限方案

# 秘钥分成 n个人保管，但是恢复秘钥至少需要 t个人数

# 计算拉格朗日差值公式得到 q(0),也就是D

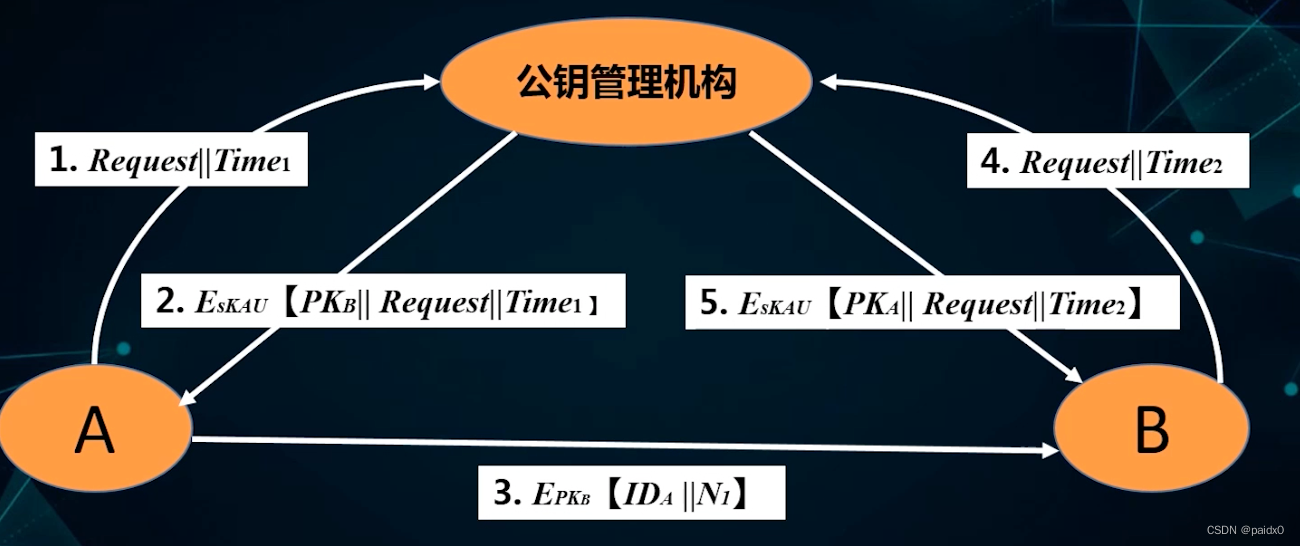
公钥管理

1、A的请求+时间戳
2、CA私钥加密(B的公钥+A的请求+时间戳)
3、A用CA的公钥解密拿到B的公钥加密(A的ID和随机数N)
4、B解密拿到A的ID，向CA请求A的公钥
5、CA返回A的公钥