数学建模--优化类模型

news2024/11/25 1:06:07

目录

一、根据目标函数约束条件类型分类

1、线性规划

①线性规划模型的一般形式

​②用MATLAB优化工具箱解线性规划

 ③模型分析    

 2、非线性规划

①非线性规划的基本概念

②非线性规划的基本解法

③二次规划

④一般非线性规划 

二、控制变量类型分类

1、整数规划

①matlab编程

②模型求解

2、混合整数规划（MIP）

①matlab语法

②模型案例

3、0-1规划

①应用范围

②案例分析

③matlab代码如下：

三、其他分类方法

1、单目标规划与多目标规划

①理想点法

 ②线性加权和法

 ③最大最小值法

 ④目标规划法

 ⑤模糊数学求解方法

2、动态规划与静态规划

①动态规划思路

②最短路径规划

3、随机规划与确定规划

①随即规划

②案例分析

一、根据目标函数约束条件类型分类

1、线性规划

①线性规划模型的一般形式

目标函数和所有的约束条件都是设计变量的线性函数。

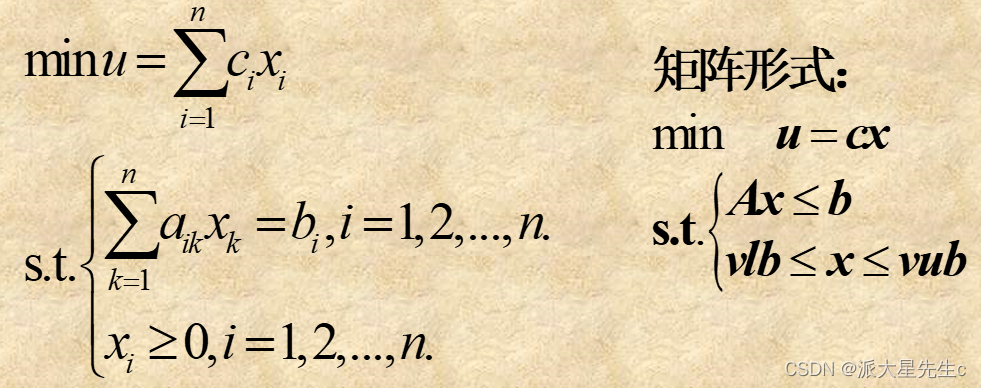
4f598fa74f7f4464892f77e4cf08e3b0.png

0f5b5ff45ae7406386969dc308201dc3.png ②用MATLAB优化工具箱解线性规划

45f709f454f64d228880b96843309d51.png

966625e195c544fdb14fc2d54f1e9fe3.png

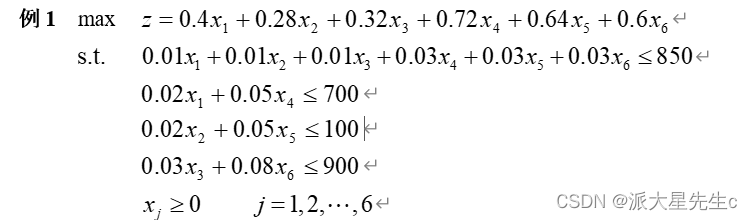
 ③模型分析    1e766a64c896487dabc303113009b7f8.png

    c=[-0.4 -0.28 -0.32 -0.72 -0.64 -0.6];
    A=[0.01 0.01 0.01 0.03 0.03 0.03;0.02 0 0 0.05 0 0;0 0.02 0 0 0.05 0;0 0 0.03 0 0 0.08];
    b=[850;700;100;900];
    Aeq=[];
    beq=[];
    vlb=[0;0;0;0;0;0];
    vub=[];
    [x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)

   55923392e80143ffa5c30e0755c334e8.png

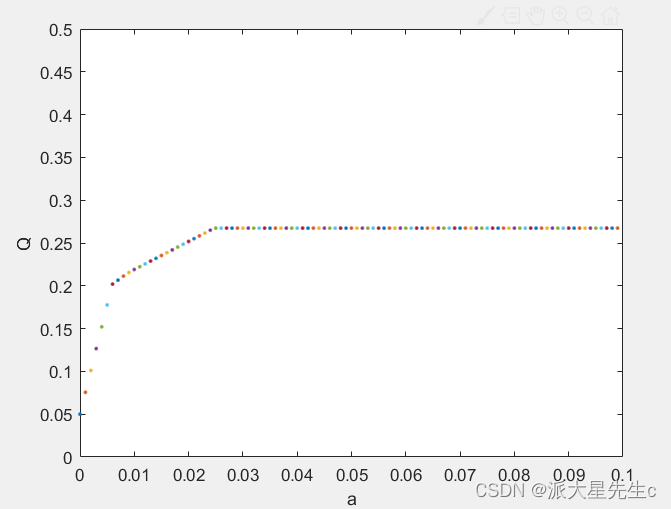
0d630580bd834b77abff913707dbd564.png 由于a是任意给定的风险度，到底怎样给定没有一个准则，不同的投资者有不同的风险度.我们从a=0开始，以步长△a=0.001进行循环搜索，编制程序如下：

a=0;
while(1.1-a)>1
c=[-0.05 -0.27 -0.19 -0.185 -0.185];
Aeq=[1 1.01 1.02 1.045 1.065];
beq=[1];
A=[0 0.025 0 0 0;0 0 0.015 0 0;0 0 0 0.055 0;0 0 0 0 0.026];
b=[a;a;a;a];
vlb=[0,0,0,0,0];
vub=[];
[x,val]=linprog(c,A,b,Aeq,beq,vlb,vub);
a
x=x'
Q=-val
plot(a,Q,'.')
axis([0 0.1 0 0.5])
hold on
a=a+0.001;
end 
xlabel('a'),ylabel('Q')

a = 0.0030  x = 0.4949      0.1200      0.2000       0.0545      0.1154      Q = 0.1266

a = 0.0060  x = 0               0.2400      0.4000       0.1091      0.2212      Q = 0.2019

a = 0.0080  x = 0.0000      0.3200      0.5333       0.1271      0.0000      Q = 0.2112

a = 0.0100  x = 0               0.4000      0.5843       0               0               Q =0.2190

a = 0.0200  x = 0               0.8000      0.1882       0               0               Q =0.2518

a = 0.0400  x = 0.0000      0.9901      0.0000       0               0               Q =0.2673

fd634e01812a49f1a603c4d5964751ef.png                 

 2、非线性规划

①非线性规划的基本概念

 定义   如果目标函数或约束条件中至少有一个是非线性函数,则最优化问题就叫做非线性规划问题

a4eb607d40ca415cb69a67a66e0ce53f.png

②非线性规划的基本解法

 罚函数法：SUTM外点法、SUTM内点法（障碍罚函数法）

近似规划法

③二次规划

a016eb1a023d49d7a036bafea3aced78.png

   用MATLAB软件求解,其输入格式如下:

   1．x=quadprog(H,C,A,b);

   2．x=quadprog(H,C,A,b,Aeq,beq);

   3．x=quadprog(H,C,A,b,Aeq,beq,VLB,VUB);

   4．x=quadprog(H,C,A,b, Aeq,beq ,VLB,VUB,X0);

   5．x=quadprog(H,C,A,b,Aeq,beq,VLB,VUB,X0,options);

   6．[x,fval]=quaprog(…);

   7．[x,fval,exitflag]=quaprog(…);

   8．[x,fval,exitflag,output]=quaprog(…);

b04526b7122942c19a54f5e944e79922.png

 写成标准式：

c598387021f246d0b2b5471030578c19.png

H=[1 -1; -1 2]; 
c=[-2 ;-6];
A=[1 1; -1 2];  
b=[2;2];
Aeq=[];
beq=[];    
VLB=[0;0];VUB=[];
[x,z]=quadprog(H,c,A,b,Aeq,beq,VLB,VUB)

 运算结果为：

x = 0.6667        1.3333
z = -8.2222

④一般非线性规划 

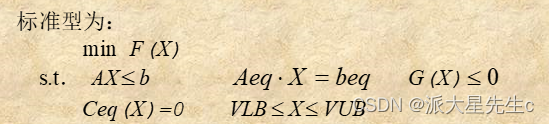
b6ab6ef253b940149436d8ac86a47993.png

1、首先建立M文件fun.m，用来定义目标函数F（X）:

2、若约束条件中有非线性约束：

G(X)或Ceq(X)=0，则建立M文件nonlcon.m定义函数G(X)与Ceq(X):

function [G,Ceq]=nonlcon(X)

G=…

Ceq=…

3、 建立主程序.求解非线性规划的函数是fmincon,命令的基本格式如下：

(1)  x=fmincon(‘fun’,X0,A,b)

(2)  x=fmincon(‘fun’,X0,A,b,Aeq,beq)

(3)  x=fmincon(‘fun’,X0,A,b, Aeq,beq,VLB,VUB)

(4) x=fmincon(‘fun’,X0,A,b,Aeq,beq,VLB,VUB,’nonlcon’)

(5)x=fmincon(‘fun’,X0,A,b,Aeq,beq,VLB,VUB,’nonlcon’,options)  

11bdcaedce864f18999518712179b360.png

(6) [x,fval]= fmincon(…)

(7) [x,fval,exitflag]= fmincon(…)

(8)[x,fval,exitflag,output]= fmincon(…)

4、例题解释

f2418c9e9c9344ea869219f9194cb500.png

 写成标准式：

96a134ac97334e168e365ff2e1b86b58.png

 先建立M-文件 fun3．m:

    function f=fun3(x);

    f=-x(1)-2*x(2)+(1/2)*x(1)^2+(1/2)*x(2)^2

再建立主程序youh2．m：

 x0=[1;1];
 A=[2 3 ;1 4]; b=[6;5];
 Aeq=[];beq=[];
 VLB=[0;0]; VUB=[];
 [x,fval]=fmincon('fun3',x0,A,b,Aeq,beq,VLB,VUB)

运行结果为：

   x = 0．7647       1．0588
   fval =   -2．0294

二、控制变量类型分类

1、整数规划

①matlab编程

利用Matlab的线性规划指令：

[x,fval]=linprog(f,A,b,Aeq,beq,lb,ub)

编写计算整数规划函数，输入与输出与上述指令相同

分枝定界法（递归实现）

function [x,fval,status] = intprog(f,A,B,I,Aeq,Beq,lb,ub,e)

%整数规划求解函数 intprog()

%     其中 f为目标函数向量

%     A和B为不等式约束 Aeq与Beq为等式约束

%     I为整数约束

%     lb与ub分别为变量下界与上界

%     x为最优解，fval为最优值

%例子:

%        maximize 20 x1 + 10 x2

%        S.T.

%                5 x1 + 4 x2 <=24

%                2 x1 + 5 x2 <=13

%                   x1, x2 >=0

%                   x1, x2是整数

% f=[-20, -10];

% A=[ 5  4; 2 5];

% B=[24; 13];

% lb=[0 0];

% ub=[inf inf];

% I=[1,2];

% e=0.000001;

% [x v s]= IP(f,A,B,I,[],[],lb,ub,,e)

% x = 4     1  v = -90.0000   s = 1



% 控制输入参数

if nargin < 9, e = 0.00001;

   if nargin < 8, ub = [];

      if nargin < 7, lb = [];

         if nargin < 6, Beq = [];

            if nargin < 5, Aeq = [];

               if nargin < 4, I = [1:length(f)];

               end, end, end, end, end, end

 

%求解整数规划对应的线性规划,判断是否有解

options = optimset('display','off');

[x0,fval0,exitflag] = linprog(f,A,B,Aeq,Beq,lb,ub,[],options);

if exitflag < 0

    disp('没有合适整数解');

    x = x0;

    fval = fval0;

    status = exitflag;

    return;

else

    %采用分支定界法求解

    bound = inf;

    [x,fval,status] = branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);

end



子函数

function [newx,newfval,status,newbound] = branchbound(f,A,B,I,x,fval,bound,Aeq,Beq,lb,ub,e)



% 分支定界法求解整数规划

% f,A,B,Aeq,Beq,lb,ub与线性规划相同

% I为整数限制变量的向量

% x为初始解，fval为初始值

options = optimset('display','off');

[x0,fval0,status0]=linprog(f,A,B,Aeq,Beq,lb,ub,[],options);



%递归中的最终退出条件

%无解或者解比现有上界大则返回原解

if status0 <= 0 || fval0 >= bound

    newx = x;

    newfval = fval;

    newbound = bound;

    status = status0;

    return;

end



%是否为整数解,如果是整数解则返回

intindex = find(abs(x0(I) - round(x0(I))) > e);

if isempty(intindex)

    newx(I) = round(x0(I));

    newfval = fval0;

    newbound = fval0;

    status = 1;

    return;

end



%当有非整可行解时，则进行分支求解

%此时必定会有整数解或空解

%找到第一个不满足整数要求的变量

n = I(intindex(1));

addA = zeros(1,length(f));

addA(n) = 1;

%构造第一个分支 x<=floor(x(n))

A = [A;addA];

B = [B,floor(x(n))];

[x1,fval1,status1,bound1] = branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);

A(end,:) = [];

B(:,end) = [];

%解得第一个分支，若为更优解则替换，若不是则保持原状



status = status1;

if status1 > 0 && bound1 < bound

    newx = x1;

    newfval = fval1;

    bound = fval1;

    newbound = bound1;

else

    newx = x0;

    newfval = fval0;

    newbound = bound;

end



%构造第二分支

A = [A;-addA];

B = [B,-ceil(x(n))];

[x2,fval2,status2,bound2] = branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);   

A(end,:) = [];

B(:,end) = [];



%解得第二分支，并与第一分支做比较，如果更优则替换

if status2 > 0 && bound2 < bound

    status = status2;

    newx = x2;

    newfval = fval2;

    newbound = bound2;

end

②模型求解

利用上述指令求解下列问题：

汽车厂生产三种类型的汽车，已知各类型每辆车对钢材、劳动时间的需求，利润及工厂每月的现有量

 

小型

中型

大型

现有量

钢材（吨）

1

2

5

1000

劳动时间（小时）

250

125

150

120000

利润（万元）

3

5

12

 

1、若每月生产的汽车必须为整车，试制订月生产计划，使工厂的利润最大？

f = [-3 -5 -12];
A = [1 2 5;250 125 150];
B = [1000 120000];
I = [1:length(f)];
lb = [0 0 0];
[x,fval,status] = intprog(f,A,B,I,[],[],lb)

答案为 x =307   344     1     fval = -2653      status =1

2、如果生产某一类型汽车，则至少要生产50辆，那么最优的生产计划应作何改变？

lb = [50 50 50]

答案为  x =350   200    50     fval =-2.6500e+003     status =1

2、混合整数规划（MIP）

①matlab语法

x = intlinprog(f, intcon,A,b)
x = intlinprog(f , intcon,A,b,Aeq, beq)
X=intlinprog(f , intcon, A, b, Aeq, beq,1b,ub)
x = intlinprog(f, intcon,A, b,Aeq, beq, lb, ub,x0)
x = intlinprog(f, intcon, A, b,Aeq, beq,lb, ub, x0, options)
x = intlinprog(problem)
[x, fval, exitflag,output] = intlinprog(__)

f、x、intcon、lb、beq、Ib和ub是向量，A和Aeq是矩阵

②模型案例

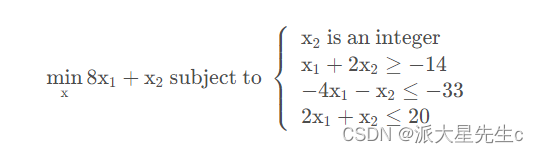
9d2bde138d984c5baf9bab6ac7fc00cf.png

f = [8;1];%确定目标函数系数
intcon = 2;%理解为两个受x受到整数限制
A = [-1,-2;
    -4,-1;
    2,1];%构造不不等式左边系数矩阵
b = [14;-33;20];%构造不等式右边矩阵
x = intlinprog(f,intcon,A,b)

 1540ec512b1041ef9a1930da6c9fc2f9.png

%案例二
clear all
clc
% 编写目标函数向量和由整数变量组成的向量。
f = [-3;-2;-1];
intcon = 3;
% 编写线性不等式约束。
A = [1,1,1];
b = 7;
% 编写线性等式约束。
Aeq = [4,2,1];
beq = 12;
% 编写边界约束。
lb = zeros(3,1);%等效于lb=[0;0;0]
ub = [Inf;Inf;1]; %强制x(3)为一个固定1
%调用intlinprog
x = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub)

当x2 = 5 , x3 = 1 , x1 = 0 最值为−12 

3、0-1规划

①应用范围

0-1线性规划模型一般被用于指派问题上面

②案例分析

 [x,f]= L01p_e(c,A,b,N)用枚举法求解下列
  0-1线性规划问题
 min f=c'*x, s.t. A*x<=b,x的分量全为整数0或1,
 其中N表示约束条件 Ax ≤ b中的前N个是等式，N= 0时可以省略。
 返回结果x是最优解，f是最优解处的函数值。
  
例 max f=3x1+5x2+2x3+4x4+2x5+3x6
 s.t. 8x1+13x2+6x3+9x4+5x5+7x6<=24, x1,…,x6均为0或1
求解
c=-[3,5,2,4,2,3];a=[8,13,6,9,5,7];b=24;
x=L01p_e(c,a,b)

L01p_e(c,a,b)

③matlab代码如下：

function [x,f]=L01p_e(c,A,b,N)
if nargin<4,N=0;end
c=c(:);b=b(:);
[m,n]=size(A);x=[];f=abs(c')*ones(n,1);i=1;
while i<=2^n
   B=de2bi(i-1,n)';
   t=A*B-b;t11=find(t(1:N,:)~=0);
   t12=find(t(N+1:m,:)>0);t1=[t11;t12];
   if isempty(t1)
      f=min([f,c'*B]);
      if c'*B==f,x=B;end
   end
   i=i+1;
end

96d6feb3a12244e4945d08d5e9d82825.png

0-1线性规划和整数规划的示例

 d8cc87ee287d460587bd1b98e09a79a1.png

 f=[-6,-2,-3,-5];
A=[-3,5,-1,-6;1,1,1,-1;1,2,4,5;];
b=[-4,3,10];
intcon=[1,2,3,4];
lb=zeros(4,1);
ub=ones(4,1);
[x,y]=intlinprog(f,intcon,A,b,[],[],lb,ub);
x,y=-y
plot(x,'--ok');

结果为：

558faf20671d4de7ba65dd0cf66fa052.png

三、其他分类方法

27720b165e6d4490942185b3768b3a54.png

1、单目标规划与多目标规划

①理想点法

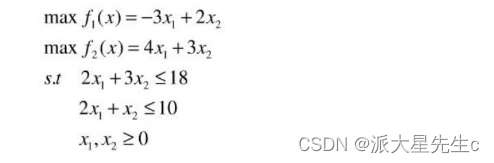
 3a362d609a0e4831bfc2eecaa7e9ea73.png

 7211d6190b9d412e953371e5af082ce3.png

d1f3f4d86c474f45a910ae4a72d5d2d1.png

 ②线性加权和法

8263e5b4cc634d03830462725d8f1889.png

 ③最大最小值法

d60b8bbae19140aea165c2a1c8cb3e88.png

 ④目标规划法

7df065a079b1493298f6f0702c5c81ec.png

 ⑤模糊数学求解方法

d7b7be04d0c140488c68e65a681c60f7.png

e1fba331a1a04a368b2db62966258edb.png

 

2、动态规划与静态规划

①动态规划思路

1、找到状态和选择，确定当前状态和转换

2、明确dp数组/或函数的定义，即dp数组保存了啥信息（dp数组一般是一维或二维）

3、寻找状态之间的关系，当前状态如何根据上一状态和一些已知信息得到（状态转换方程）

②最短路径规划

import matplotlib.pyplot as plt
import pylab as pl
import connmysql
import pandas as pd

sql2 = "SELECT id, distance,duration FROM  trafic"
checklist = connmysql.getdata(sql2)
ids=[]
for i in range(0,len(checklist)):
    ids.append(checklist[i][0])
time_dataframe = pd.DataFrame(columns=['distance','duration'], index=ids)
# print(time_dataframe)
for i in range(0,len(checklist)):
    id=checklist[i][0]
    time_dataframe.at[ids[i],'distance'] = float(checklist[i][1])#distance
    time_dataframe.at[ids[i], 'duration'] = float(checklist[i][2] ) # distance
# id='100001-100002'
# print(time_dataframe.at[id,'distance'])
# print(time_dataframe.at['100001-100002','duration'])
# list=['100002','100003','100004','100005','100006']
        #基于动态规划求得最短路径，计算量会比较小，速度较快
list = ['100002', '100003', '100004', '100005', '100006']
# 基于动态规划求得最短路径，计算量会比较小，速度较快
routelist=[]
route_distance=[]
for j in range(0,len(list)-1):
    print('mm',j)
    print('he1', routelist)
    print('he2', route_distance)
    ids = []
    distances, routes = {}, {}
    for i in range(0, len(list)):
        if len(routelist)==0:#当里面还没有目标在时
            id = list[0] + '-'+list[i]
            if list[i]!=list[0]:
                ids.append(id)
        else:
            if list[i] not in routelist :#计算过的点不再重复计算
                id =  routelist[j]+ '-'+list[i]
                ids.append(id)
    print('he3',ids)
    for k in range(0, len(ids)):
        distances[ids[k]] = time_dataframe.at[ids[k], 'distance']
    print('he4',distances)
    route1 = sorted(distances.items(), key=lambda item: item[1])  # 将最小距离取出来
    route_distance.append(route1[0])
    # routes[route1[0][0]] = route1[0][1]  # key:100002-100006,values: 3929.0,,保存离最后一个点的最优路线
    print('he5',route1)
    a=route1[0][0].split('-')
    if a[0] not in routelist:
        routelist.append(a[0])
    if a[1] not in routelist:
        routelist.append(a[1])
    print('he6', routelist)
print('he',routelist)

3、随机规划与确定规划

①随即规划

运用随机动态规划的分析方法，求解随机动态规划模型的最优解是一种比较常见的数学建模问题。例如，在实际应用中，经常会遇到某些多阶段决策过程中出现随机因素的情况，而动态规划的方法也可以处理这种随机性问题。

②案例分析

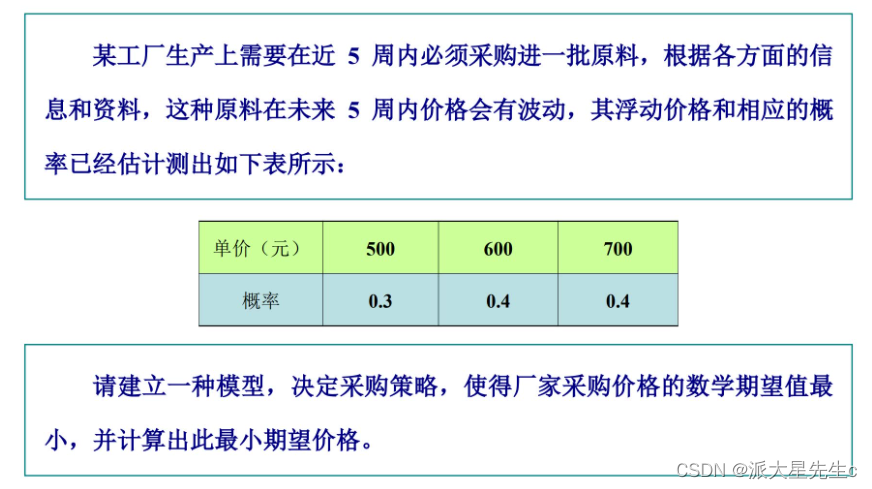
b9f8e8146f0441029b7f8de66c11a567.png

 分析并假设

此问题中价格是一个随机变量，是按照某种已知的概率分布规律取值的。可以将采购期限内的5周看做5个阶段（即需要每周做一次决策，自然也可以每天做一次决策而将之更加细致地分为35个阶段，则问题便成了在每个阶段进行决策是否购进原料，以期使原料的采购价格的期望值达到最小。

在实际应用中，经常会遇到某些多阶段决策过程中出现随机因素的情况。用动态规划的方法也可以处理这种随机性问题。不过此时状态转移不能完全确定，而是按照某种已知的概率分布取值，具有这种性质的多阶段决策过程就称之为随机性的决策过程，此时运用的动态规划也就相应的被称为随机动态规划。

dc203953d6294220927ab2a58a94d8a4.png a153249b0848486c869ae00d34e1f8c6.png

 模型的建立和求解e9f9045464ba4ce580de09f28add3b45.png

 e093c3869c384ae28cd21259cfa73a4d.png

 ebba08705e394a52b590de1891108b3c.png

 cd72fd1e8c8c484390b9449bd15a6971.png

fca5508b9c40418aa81fb5a386e37094.png 8a6616650dfc4503846663508036b5b5.png

 69762878623546f3a866b304f98701a3.png

 结论与分析

 由以上逆推计算得结果可知，最优的采购策略序列为{,,,,}u1u2u3u4u5。根据u1，u2，3u的表达式可知，在第1、2、3周时，若价格为500时，就应采购；而在价格为600或者700时则应采取等待观望的态度。

由u4的表达式得，在第4周，若价格为500或者600时就应该采购，而在价格为700时则等待观望。

若在前4周都采取了等待观望策略，则在第5周，无论什么价格都必须采购（u5=1）。

 

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/4698.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

总结线程安全问题的原因和解决方案

总结线程安全问题的原因和解决方案

一. 线程安全问题 概念 首先, 线程安全的意思就是在多线程各种随机调度的情况下, 代码不出现 bug 的情况. 如果在多线程调度的情况下, 出现 bug, 那么就是线程不安全. 二. 观察线程不安全的情况 下面我们用多线程来累加一个数, 观察线程不安全的情况: 用两个线程, 每个线程…
阅读更多...
树--堆和优先权队列

树--堆和优先权队列

数据结构中的堆和栈与操作系统内存划分中的堆和栈没有关系 一、堆的定义 一个大小为n的堆是一棵包含n个结点的完全二叉树&#xff0c;其根节点称为堆顶。 根据堆中亲子结点的大小关系&#xff0c;分为大堆和小堆&#xff1a; &#xff08;1&#xff09;最小堆&#xff1a;树中…
阅读更多...
高斯原型网络原论文高质量翻译

高斯原型网络原论文高质量翻译

论文地址&#xff1a;Gaussian Prototypical Networks for Few-Shot Learning on Omniglot 文章目录摘要1 引言1.1 Few-shot learning1.2 高斯原型网络2 相关工作3 方法3.1 编码器3.2 偶发性训练3.3 定义一个类3.4 评估模型4 数据集5 实验5.1 协方差估计的用法6 结论摘要 我们…
阅读更多...
万字长文解读计算机视觉中的注意力机制（附论文和代码链接）

万字长文解读计算机视觉中的注意力机制（附论文和代码链接）

文中论文和代码已经整理&#xff0c;如果需要&#xff0c;点击下方公众号关注&#xff0c;领取&#xff0c;持续传达瓜货 所向披靡的张大刀 注意力机制是机器学习中嵌入的一个网络结构&#xff0c;主要用来学习输入数据对输出数据贡献&#xff1b;注意力机制在NLP和CV中均有使…
阅读更多...
目标检测算法——YOLOv5/YOLOv7改进之结合无参注意力SimAM

目标检测算法——YOLOv5/YOLOv7改进之结合无参注意力SimAM

目录 &#xff08;一&#xff09;前言介绍 1.摘要 2.不同注意力步骤比较 &#xff08;二&#xff09;相关实验 &#xff08;三&#xff09;YOLOv5结合无参注意力SimAM 1.配置.yaml文件 2.配置common.py 3.修改yolo.py SimAM&#xff1a;无参数Attention助力分类/检测/分…
阅读更多...
点云应用——三维空间边界点排序+机器人轨迹引导（1）

点云应用——三维空间边界点排序+机器人轨迹引导（1）

三维空间边界点排序机器人轨迹引导一、前言二、思路一&#xff1a;利用重建思路三、思路二&#xff1a;利用PCL边界提取方法三维空间点排序四、后续一、前言 最近做了点云边界提取、并实时发送至机器人进行引导的研究&#xff0c;主要遇到了两个问题&#xff1a; 1&#xff09;…
阅读更多...
Python画爱心——一颗会跳动的爱心~

Python画爱心——一颗会跳动的爱心~

节日就快到来了&#xff0c;给你的Ta一个惊喜吧~ 今天给大家分享一个浪漫小技巧&#xff0c;利用Python制作一个立体会动的心动小爱心 成千上百个爱心汇成一个大爱心&#xff0c;从里到外形成一个立体状&#xff0c;给人视觉上的冲击感&#xff01;浪漫极了↓ 微信扫码添加&a…
阅读更多...
CUDA 从入门到放弃(一)

CUDA 从入门到放弃(一)

CUDA从入门到放弃系列包含内容 异构并行计算CUDA编程模型CUDA执行模型CUDA内存CUDA流和并发CUDA指令级原语GPU加速库多GPU编程 本文你将了解到 异构并行计算CUDA编程模型 温馨提示: 本文可能引发C/C零基础的读者不适,请谨慎观看. 一、聊聊异构并行计算 异构并行计算的本质是…
阅读更多...
MQTT Broker mosquito配置以及使用tls证书登录附上Python调用代码

MQTT Broker mosquito配置以及使用tls证书登录附上Python调用代码

MQTT Broker mosquito配置以及使用tls证书登录 文章目录MQTT Broker mosquito配置以及使用tls证书登录1. 前言2. 安装3. mosquito相关命令3.1 运行停止查看状态3.2 创建可以登录mosquito的用户3.3 配置权限规则文件3.4 配置mosquito3.5 使用mosquito_pub和mosquito_sub测试3.5.…
阅读更多...
web手势库Alloyfinger

web手势库Alloyfinger

前言 在上一篇文章 前端pdf预览、pdfjs的使用&#xff0c;我们使用pdf.js 来实现了pdf的预览。但是客户车间里的电脑是触摸屏&#xff0c;要求能够手势放大图纸&#xff0c;能够拖动图纸。最终决定使用 Alloyfinger 来解决手势的问题。 官方github https://github.com/Alloy…
阅读更多...
计算机网络(一)：计算机网络概念、功能、组成

计算机网络(一)：计算机网络概念、功能、组成

计算机网络的概念 计算机网络&#xff1a;是一个将分散的、具有独立功能的计算机系统&#xff0c;通过通信设备与线路连接起来&#xff0c;由功能完善的软件实现资源共享和信息传递的系统 计算机网络是互连的、自治的计算机集合。 互连&#xff1a;互联互通 自治&#xff1a;无…
阅读更多...
前端面经 前端优化

前端面经 前端优化

前端面经 前端优化 文章目录前端面经 前端优化HTTP/2 Web优化最佳实践DNS与解析如何使用CDN分发缓存策略页面渲染优化避免CSS、JS阻塞CSS阻塞JS的阻塞改变JS阻塞的方式使用字体图标iconfont代替图片图标降低CSS选择器的复杂性减少重绘和回流如何避免图片资源优化Webpack优化降低…
阅读更多...
【Vue】VueCLI 的使用和单文件组件（1）

【Vue】VueCLI 的使用和单文件组件（1）

学习内容&#xff1a; 1&#xff09;了解一下 Vue 的脚手架工具&#xff1b; 2) 认识一下 Vue 里面的单文件组件。‍‍ 在真正开发大型项目的时候&#xff0c;实际上我们并不能通过一个这样的index点html的方式去编写一个比较大型的项目&#xff0c;‍‍ 所以我们要学习使用 V…
阅读更多...
JavaScript 69 JavaScript Web API 69.3 Web History API

JavaScript 69 JavaScript Web API 69.3 Web History API

JavaScript 文章目录JavaScript69 JavaScript Web API69.3 Web History API69.3.1 History back() 方法69.3.2 History go() 方法69.3.3 History 对象属性69.3.4 History 对象方法69 JavaScript Web API 69.3 Web History API Web History API 提供了访问 windows.history 对…
阅读更多...
Linux进程与操作系统详解

Linux进程与操作系统详解

文章目录一&#xff1a;冯诺依曼体系二&#xff1a;操作系统三&#xff1a;进程和PCB四&#xff1a;进程相关的指令五&#xff1a;getpid和getppid系统调用六&#xff1a;fork系统调用七&#xff1a;进程状态八&#xff1a;Linux下进程状态大全8.1&#xff1a;R(running)8.2&am…
阅读更多...
Hive3 - HiveSQL 特征及操作

Hive3 - HiveSQL 特征及操作

一、HiveSQL特征 Hive SQL&#xff08;HQL&#xff09;与SQL的语法大同小异&#xff0c;基本上是相通的&#xff0c;对SQL掌握的可以非常快的上手使用Hive SQL。不过在一些细节上需要特别注意Hive自己特有的语法知识点&#xff0c;下面分别进行介绍。 1. 字段数据类型 Hive数…
阅读更多...
【附源码】Python计算机毕业设计烹饪课程预约系统

【附源码】Python计算机毕业设计烹饪课程预约系统

项目运行 环境配置&#xff1a; Pychram社区版 python3.7.7 Mysql5.7 HBuilderXlist pipNavicat11Djangonodejs。 项目技术&#xff1a; django python Vue 等等组成&#xff0c;B/S模式 pychram管理等等。 环境需要 1.运行环境&#xff1a;最好是python3.7.7&#xff0c;…
阅读更多...
电脑重装系统c盘如何备份资料

电脑重装系统c盘如何备份资料

现在越来越多的用户都喜欢重装自己所喜欢的电脑系统&#xff0c;但需要在重新安装系统之前备份自己的电脑。因此有很多用户问重装系统c盘如何备份的文件。今天小编就教下大家重装系统c盘如何备份的教程。 工具/原料&#xff1a; 系统版本&#xff1a;windows7系统 品牌型号&…
阅读更多...
多目标应用：非支配排序的鲸鱼优化算法NSWOA优化RBF神经网络实现数据预测（RBF隐藏层神经元个数可以自行设定）

多目标应用：非支配排序的鲸鱼优化算法NSWOA优化RBF神经网络实现数据预测（RBF隐藏层神经元个数可以自行设定）

一、非支配排序的鲸鱼优化算法 非支配排序的鲸鱼优化算法&#xff08;Non-Dominated Sorting Whale Optimization Algorithm&#xff0c;NSWOA&#xff09;由Pradeep Jangir和 Narottam Jangir于2017年提出。 NSWOA算法流程如下&#xff1a; 二、RBF神经网络 1988年&#xf…
阅读更多...
Spring-Aop面向切面编程

Spring-Aop面向切面编程

文章目录一、简介1、作用2、AOP核心概念3、五种&#xff08;增强&#xff09;通知类型二、AOP入门小案例&#xff08;注解版&#xff09;1.导入坐标(pom.xml)2.制作连接点(原始操作&#xff0c;Dao接口与实现类)3:定义通知类和通知4:定义切入点5:制作切面6:将通知类配给容器并标…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023