题目描述

设计一个算法，算出 n 阶乘有多少个尾随零。

示例 1:

• 输入: 3
• 输出: 0
• 解释: 3! = 6, 尾数中没有零。

示例 2:

• 输入: 5
• 输出: 1
• 解释: 5! = 120, 尾数中有 1 个零

说明: 你算法的时间复杂度应为 O(log n) 。

解题思路与代码

这道题，乍一看很简单，实则还是考到了点其他的数学知识的。

比如：

• 阶乘的计算：题目要求计算 n!，也就是 n 阶乘。n 阶乘表示从 1 到 n 的所有整数的乘积，即 n! = 1 × 2 × 3 × … × n。

• 数学知识 - 因子：这道题的关键是理解尾随零是由因子 2 和 5 相乘得到的。在 n! 的因式分解中，我们需要找到因子 2 和 5 的数量。

• 优化算法：题目要求算法的时间复杂度为 O(log n)，这意味着我们需要找到一种有效的方法来计算 n! 中因子 5 的个数。在这个过程中，我们发现因子 2 的个数总是多于因子 5 的个数，因此我们只需计算 n! 中有多少个因子 5。通过不断地将 n 除以 5，我们可以找到所有的因子 5，从而有效地降低时间复杂度。

• 避免整数溢出：原始代码试图计算 n! 的值，但这在 n 较大时可能导致整数溢出。优化后的代码通过计算因子 5 的个数来避免了这个问题，因为我们不需要实际计算 n! 的值。

具体代码如下：

class Solution {
public:
    int trailingZeroes(int n) {
        int count = 0;
        while (n >= 5) {
            n /= 5;
            count += n;
        }
        return count;
    }
};

复杂度分析

时间复杂度：O(logn)
空间复杂度：O(1)

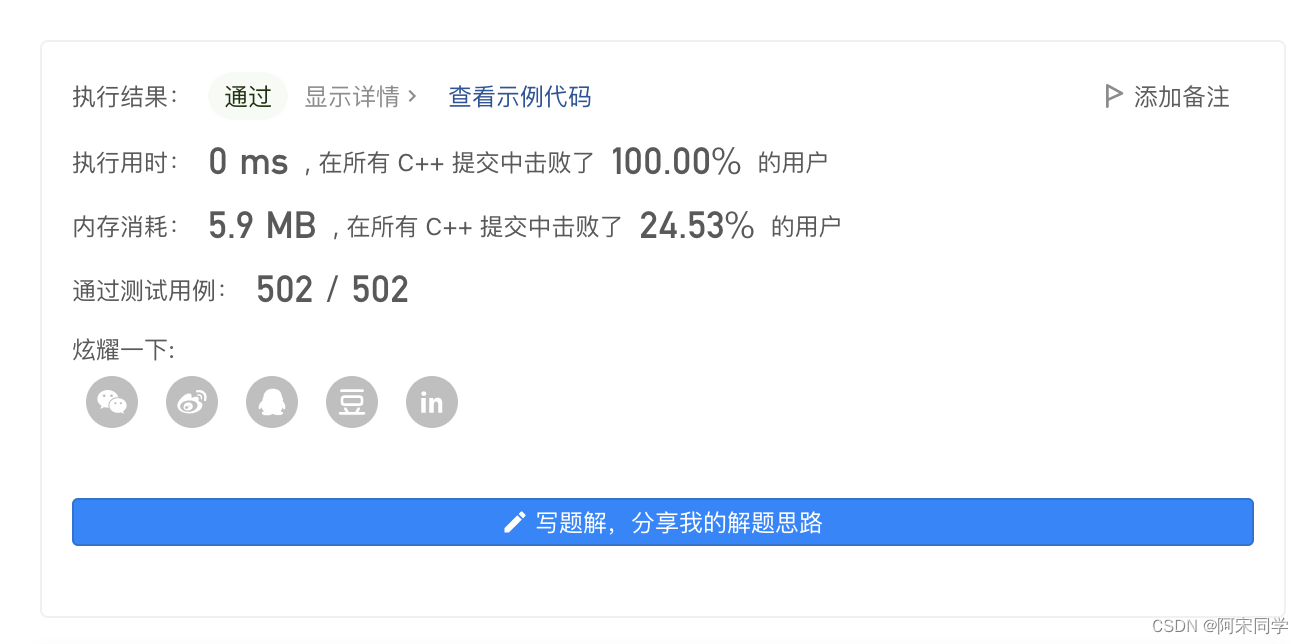
总结

这道题考到了数论，因子计数的数学概念，如果你不了解这些数学概念，这道题还真不是一道简单的题。