美联储加息已狂飙一年,很多相关预测美联储加息降息的文章都会提到“一年内加息多少次的概率是多少多少”这种表述,那么这个数据是怎样计算的?本期笔者将简单讨论美国联邦利率的运作机制,介绍用于预测联储加/降息概率的方式,并主要从定量的角度分析其有效性。本文发现利用期货合约预测目标利率有效性欠佳,但期货合约对联邦基金利率预测有效性较好。本文属于一期杂谈,主要内容如下:
目录
1. 美国联邦基金利率的运作机制
2. 如何预测联邦基金目标利率
3. 实证检验
3.1 数据准备
3.2 目标利率与期货合约数据分析
3.2.1 数据平稳性检验
3.2.2 格兰杰因果关系检验
3.2.3 方差分解与脉冲响应分析
3.2.4 回归分析
3.3 联邦基金利率与期货合约数据分析
3.3.1 因果检验
3.3.2 回归分析
4. 实证检验结果
5. 总结
6. 参考文献
7. 附录
8. 系列精选
1. 美国联邦基金利率的运作机制
美联储作为美国中央银行,公开市场操作是做为一个央行最基本的经济调控手段。美联储的公开市场操作就是美联储通过买卖美国国债来影响联邦基金利息率(Federal fund rate,FFR)。
美国联邦基金利率其实就是存款类金融机构(可以简单理解成银行)间市场的无抵押隔夜拆借利率,可以直接对标我国的SHIBOR,英国的LIBOR。联邦基金利率虽然是银行间的拆借行为,但美联储毕竟是带头大哥,小弟怎么办事始终是要看大哥的脸色。于是,美联储的公开市场操作就可以对联邦基金利率间接造成影响。举个例子:美联储放水,那么公开市场操作便可以通过国债逆回购的方式,将商业银行手里的国债买过去(向银行市场上撒币)。市场上有更多钱了,银行想借/贷给别的银行都更容易,风险也较低,于是进行同业拆借时的利率自然也就低了。
因为市场上有很多家银行,每家拆借的利率都是不同的,因此每个交易日早上9点,美联储会公布前一个工作日拆借利率的中间值作为有效联邦基金利率(Effective federal fund rate,EFFR没有期限结构,均为隔夜利率)。
作为制定货币政策的带头大哥,央行当然要保持货币政策的稳定性,总不能今天突然想放水,明天又收回去。因此美联储又成立了个公开市场操作委员会(Federal open market committee, FOMC),每年开八次会议,一帮老头子开会定出一个联邦基金利率的目标区间作为指导,又称为目标利率(Federal fund target rate,糟老头们每年开八次会议,这个目标利率会被写在会议纪要里)。目标利率一般是以25个基点为区间,每次目标利率的升降也是以25个基点为单位进行,未来的公开市场操作目的就是让联邦基金利率往这个目标区间里靠拢。
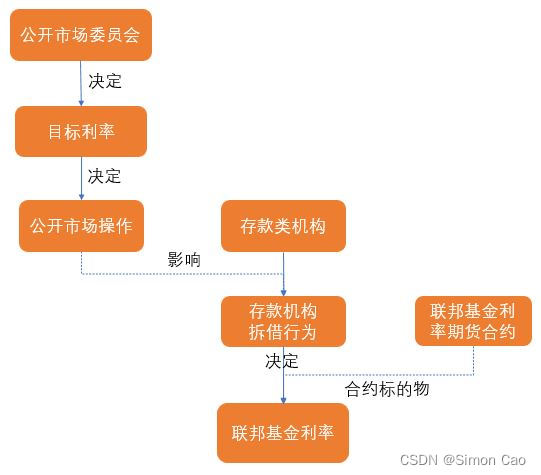
图一:联邦基金利率的传导机制
理解笔者上面所谈的这几个概念和运作逻辑相当重要,后面这几个粗体名词会频繁出现,并且这个传导机制有利于理解数据分析的结论。至于其它关于美联储利率对资产定价的重要性,还有其它一些货币政策操作,网上文章铺天盖地就不做多谈了。笔者筛选了一篇写得还挺全的文章以供参考(余永定, 2022)【1】。
2. 如何预测联邦基金目标利率
联邦基金利率是有期货市场的,合约详细信息可以访问芝加哥商品期货交易所(CME)【2】。目前市场上最主流的预测方案是通过联邦基金利率期货合约推测未来目标利率区间上涨/下跌的可能性(Keasler & Goff,2007)【3】。公式如下:
这个公式看上去很长,但其实是个经验公式,没有任何推导。分子是市场期货合约的利率水平-当期目标利率区间均值,分母是预测区间均值-当期目标利率区间均值。【3】这篇论文里没有提到笔者所写的目标区间的均值,而是表述为“The current fed funds rate”,那是因为这篇论文是07年写的,08年以前目标利率是一个确定的值,压根还不是一个区间。
结合图二举个例子说明:假设当前目标区间是[0,25]基点,当前市场上期货合约隐含的利率为30个基点。那么,未来市场目标区间上升到[25,50]基点这个区间的概率是,即
。
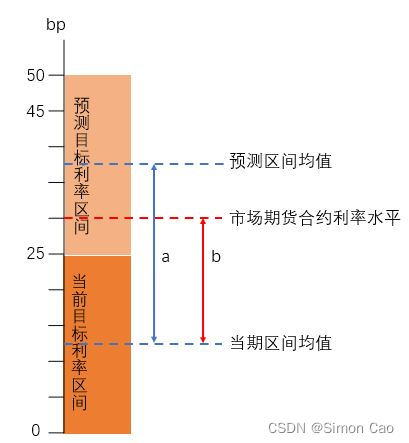
图二:预测原理
因为一次加息都是标准的25个基点,如果预测一年内加息两次即是a=50个基点,在此基础上利用公式计算概率。如果设置不同的加息阈值计算概率,就可以得到一个加息次数的概率分布。如果基于不同到期日的合约计算加息一次的概率,那么就可以得到在时间维度上加息一次的概率分布。
这个式子其实也是有问题的,如果b如果大于a,那么算出来的概率是大于100%的;b如果是负数,算出来的概率是小于0的。因此实务中这个式子往往会被魔改,加上全概率进行计算或者加上概率的限制条件。像彭博,芝加哥商品交易所都有自己的预测方法,但核心基本都需要用到期货数据进行预测。关于预测方案也不是本期的主要内容,笔者筛选了鹏扬基金施红俊(2023)【4】所写的文章以供参考。
3. 实证检验
这一预测模型的基础是建立在期货市场可以预测现目标利率的前提下。为了检验其有效性,笔者利用数据进行验证。因为这次需要检验两个变量的因果关系,不能一上来就直接搞回归那一套,因此笔者设计了检验框架如下:
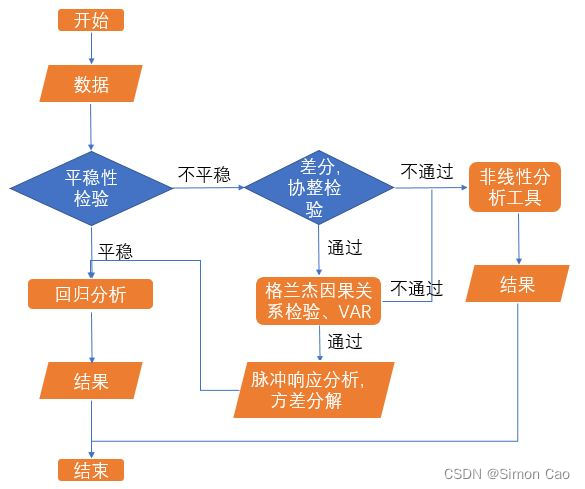
图三:检验框架
3.1 数据准备
数据获取不是本期重点,因此相关的数据和程序代码笔者都上传到资源里了,通过下面这个链接可以下载,需要5积分:美国联邦基金利率数据,目标利率数据,及利率期货数据资源。
首先是爬取联邦基金利率及目标利率数据,由于笔者的数据库没有联邦基金利率的高频数据,因此通过爬虫获取。运行爬虫程序后输出数据表如下,2000年七月至今共5千行数据。数据内容包含联邦有效基金利率及公开市场委员会目标利率的上下区间,需要注意的是2008年之前公开市场委员会目标利率是一个确定的值,还不是一个区间,因此只有一个数据:
print(data_set)
date FFR target_low target_up
2000-07-03 7.03 6.50
2000-07-05 6.52 6.50
2000-07-06 6.51 6.50
2000-07-07 6.42 6.50
2000-07-10 6.51 6.50
... ... ... ...
2023-04-17 4.83 4.75 5.00
2023-04-18 4.83 4.75 5.00
2023-04-19 4.83 4.75 5.00
2023-04-20 4.83 4.75 5.00
2023-04-21 4.83 4.75 5.00
5733 rows × 3 columns下面获取联邦基金利率期货合约的市场数据,笔者发现芝加哥商品交易爬取的难度非常大,通过交易所的API要获取这样的高频数据接口也是要钱的,因此这部分数据通过不要钱的investing.com下载获取(需要魔法才能访问,感谢提供笔者魔法的Liya)。笔者一样准备了下载好的数据表,直接读取资源中的excel表格如下:
futures = pd.read_excel("美国联邦基金利率期货数据.csv")[::-1]
print(futures)
Date Price Open High Low Change %
4621 01/03/2005 97.75 97.750 97.760 97.75 0.00%
4620 01/04/2005 97.75 97.750 97.760 97.75 0.00%
4619 01/05/2005 97.75 97.750 97.750 97.75 0.00%
4618 01/06/2005 97.75 97.750 97.750 97.75 0.00%
4617 01/07/2005 97.75 97.750 97.760 97.75 0.00%
... ... ... ... ... ... ...
4 04/20/2023 95.17 95.170 95.173 95.17 0.00%
3 04/21/2023 95.17 95.170 95.173 95.17 0.00%
2 04/23/2023 95.17 95.170 95.170 95.17 0.00%
1 04/24/2023 95.17 95.170 95.173 95.17 0.00%
0 04/25/2023 95.17 95.173 95.173 95.17 0.00%3.2 目标利率与期货合约数据分析
既然是预测公开市场委员会的目标利率,主要研究的变量就是目标利率与期货合约数据。上面这两个数据表的数据是需要处理一下的, 笔者就直接将目标利率数据合并进futures表格里了。稍微再拓展个联邦基金利率期货合约报价的知识点:合约的报价=100-EFFR,也就是说其隐含的EFFR=100-期货合约价格:
data_set.index = pd.to_datetime(data_set.index, format="%Y/%m/%d").strftime("%Y%m%d")
futures["Date"] = pd.to_datetime(futures["Date"], format='%m/%d/%Y').dt.strftime("%Y%m%d")
futures.set_index("Date", inplace=True)
futures["futures_rate"] = 100 -futures["Price"] # 期货合约价格转换为利率公式
futures["target_rate"] = data_set["target_mean"] # 取目标区间的中间值作为目标利率
futures = futures.fillna(method="ffill") # 向下填充空值可视化一下历史数据,图中蓝线为目标利率,橙线为期货合约利率:

图四:目标利率,期货合约利率历史走势
3.2.1 数据平稳性检验
设显著度水平5%,利用DF检验后两次P值分别为0.86和0.65,说明是不平稳的。
# DF平稳性检验
import statsmodels.api as sm
result = sm.tsa.stattools.adfuller(data['target_rate'])
print('target_rate p-value:', result[1])
# target_rate p-value: 0.8648820544762602
result = sm.tsa.stattools.adfuller(data['futures_rate'])
print('futures_rate p-value:', result[1])
# futures_rate p-value: 0.6557108233835188按照流程,不满足平稳性时进行差分后再次检验平稳性。不过笔者这里将数据进行二十一阶差分后除以期初数,计算成一个21天增长率的概念。为什么需要二十一阶差分呢,因为目标利率公布后会持续很长时间保持在同一个数字。只进行一阶差分只能在公布目标利率的那天产生一个增长,其余时间均是0,这样不利于后续的模型识别。至少需要21天(一个月的交易日,对应期货的月度合约)才能将加息的效果体现出来。下面生成两个新的增长率变量,看21天的时间范围内是否有加息动作,最后生成可视化走势图:
futures["futures_rate_pct"] = (futures["futures_rate"] - futures["futures_rate"].shift(21))/ futures["futures_rate"].shift(21)
futures["target_rate_pct"] = (futures["target_rate"] - futures["target_rate"].shift(21))/ futures["target_rate"].shift(21)
futures.dropna(inplace=True)
plt.figure(figsize=(12,5))
plt.plot(futures.index, futures["futures_rate_pct"], label="futures_pct")
plt.plot(futures.index, futures["target_rate_pct"], label="target_pct")
plt.xticks(futures.index[::250], rotation=90)
plt.legend()
plt.show()
图五:目标利率及期货合约变化率历史走势
转化完成后继续DF测试,这次P值均几乎为0,说明数据已平稳:
# 平稳性检验
result = sm.tsa.stattools.adfuller(futures['target_rate_pct'])
print('target_rate_pct p-value:', result[1])
# target_rate_pct p-value: 1.0145335266094929e-08
result = sm.tsa.stattools.adfuller(futures['futures_rate_pct'])
print('futures_rate_pct p-value:', result[1])
# futures_rate_pct p-value: 2.88087061001318e-08既然数据是平稳的,协整检验就不做了。
3.2.2 格兰杰因果关系检验
进行格兰杰因果关系检验,看目标利率数据与期货合约数据因果关系。先拟合一个向量自回归模型,利用AIC确定最佳拟合优度的滞后项为31,最后利用这个滞后阶数进行格兰杰因果关系检验:
model = VAR(futures[['target_rate_pct','futures_rate_pct']]) # 拟合 VAR 模型
lag_order = model.select_order() # 确定最佳的滞后阶数
# print(lag_order.summary())
model_fitted = model.fit(maxlags=lag_order.aic, ic='aic') # 拟合最佳滞后阶数的 VAR 模型
# 进行 Granger 因果关系检验
granger_test = model_fitted.test_causality('futures_rate_pct','target_rate_pct', kind='f')
print(granger_test.summary())运行后检验结果如下,格兰杰因果关系证明目标利率数据与期货合约数据存在因果关系。如果按常理来推断未来目标利率其实是造成期货合约数据变化的原因(只是从统计上看,实际上原因的时间点不应该出现在结果之前),但这个关系的大小和方向性还需进一步验证:
Granger causality F-test.
H_0: target_rate_pct does not Granger-cause futures_rate_pct.
Conclusion: reject H_0 at 5% significance level.
================================================
Test statistic Critical value p-value df
------------------------------------------------
7.252 1.452 0.000 (31, 9014)
------------------------------------------------3.2.3 方差分解与脉冲响应分析
1):下面进行方差分解,分解协方差矩阵来确定各个变量对总方差的贡献度:
fevd = model_fitted.fevd(31) # 前31期的方差分解
print(fevd.summary())结果比较长,笔者放在文末附录了(FEVD for target_rate表)。从方差分解结果来看,滞后31期的期货数据可以解释60%的目标利率方差变化,剩余40%被目标利率自己解释掉了。说明期货数据对未来目标利率的波动具有较强的解释力度。
2):下面进行脉冲响应分析,看期货数据的一个单位脉冲对目标利率造成的影响:
irf = model_fitted.irf(31) # 31期的脉冲响应分析
irf.plot(orth=False, plot_stderr=True)
plt.xticks(np.arange(0, 31, 5))主要需要关注的是图六右上角子图,即期货对目标利率的影响(现实情况是目标利率数据并非是公开市场委员会看市场期货决定的,但这里的逻辑是期货利率对未来会不会加息有没有解释力,因此从统计上需要看期货数据对未来目标利率的影响,有点绕)。
从方向上看,期货数据产生的脉冲响应(正交)均位于0轴上方(右上角子图),说明造成了同向影响,即今天如果观察到期货数据上升未来大概率会看到议息会议加息。从力度上看,y轴最大值0.04,说明在改时间点的一个单位的脉冲变化会导致目标利率产生0.04个单位的同向改变。并且,大于15个滞后期之后冲击的影响会逐渐减弱。
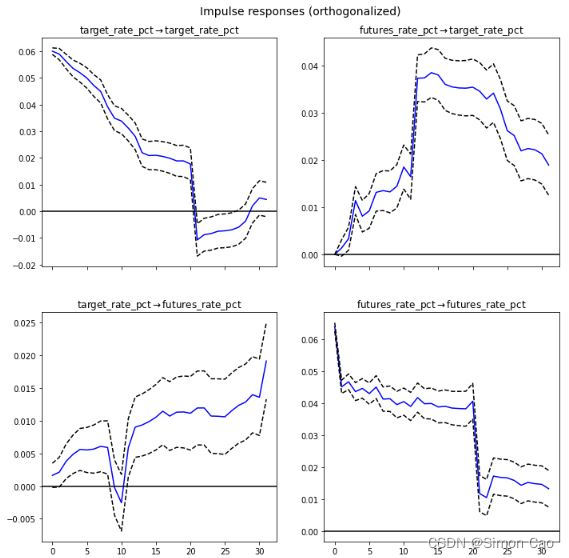
图六:脉冲响应分析图(期货合约与目标利率)
因果关系小结:1)格兰杰因果关系证明期货数据与目标利率间存在因果关系;2)期货数据对未来目标利率的波动具有较强的解释力度;3)期货数据产生的脉冲响应分析说明该关系是同向影响。
3.2.4 回归分析
上面进行了较为严谨的因果分析验证,不过仅仅确认了数据的稳定性和因果关系,接下来进行回归分析看解释力度究竟几何。虽然上面因果分析输出的最佳滞后项为31天,但笔者考虑到合约毕竟是月度的,就按21个交易日创建滞后变量。使用期货滞后项对目标利率进行回归,模型解释力为0.199,笔者对这个结果不是特别满意。
futures["futures_rate_leg"] = futures["futures_rate"].shift(21) # 创建滞后变量,用过去期货数据解释未来目标利率
model = smf.gls(data=futures, formula="target_rate_pct~futures_rate_pct_leg")
result = model.fit()
print(result.summary())
GLS Regression Results
==============================================================================
Dep. Variable: target_rate_pct R-squared: 0.199
Model: GLS Adj. R-squared: 0.199
Method: Least Squares F-statistic: 1137.
========================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------------
Intercept 0.0157 0.003 4.715 0.000 0.009 0.022
futures_rate_pct_leg 0.4908 0.015 33.722 0.000 0.462 0.519
==============================================================================笔者又计算了条件熵的信息增益,得到的结果依然是20%左右。笔者认为期货作为重要的媒介,如果需要预测公开市场委员会未来加息的概率就需要保证期货数据对未来目标利率有较强的解释力度。20%对于很多飘忽不定的现实数据来说已经不算低了,但如果仅仅只有20%左右是不够的,就好比在问一个醉汉他下一步要前后左右哪个方向走,四个方向即便是瞎猜也有25%的准确率,何况是目标利率只有加息降息不变这三种情况。
3.3 联邦基金利率与期货合约数据分析
一个事实其实一直被忽略了:期货合约的标的物为联邦基金利率,并非目标利率,因此笔者重新对期货合约及联邦基金利率进行分析。之前futures数据表已经被笔者玩得面目全非了,下面重新读取并创建数据表,合并联邦基金利率进futures表:
futures = pd.read_csv("美国联邦基金利率期货数据.csv")[::-1]
# 改为统一的日期格式
futures["Date"] = pd.to_datetime(futures["Date"], format='%m/%d/%Y').dt.strftime("%Y%m%d")
data_set.index = pd.to_datetime(data_set.index, format="%Y/%m/%d").strftime("%Y%m%d")
futures.set_index("Date", inplace=True)
futures["futures_rate"] = 100 -futures["Price"] # 计算合约利率
futures["FFR"] = data_set["FFR"] # ,按日期索引合并
futures = futures.fillna(method="ffill")
# 根据之前的数据平稳化经验,生成变化率数据
futures["futures_rate_pct"] = (futures["futures_rate"] - futures["futures_rate"].shift(21))/ futures["futures_rate"].shift(21)
futures["FFR_pct"] = (futures["FFR"] - futures["FFR"].shift(21))/ futures["FFR"].shift(21)
futures["futures_rate_pct_leg"] = futures["futures_rate_pct"].shift(21) # 生成滞后项
futures.dropna(inplace=True)可视化:
plt.figure(figsize=(8,4))
futures["futures_rate_pct"].plot(label="Futures")
futures["FFR_pct"].plot(label="FFR")
plt.legend()
plt.show()
图七:期货合约及联邦基金利率时间序列数据
3.3.1 因果检验
该走的流程还是要做的,稳定性分析,因果检验。代码结构和之前一样,笔者就只放结果了。
1):稳定性检验:通过
futures_rate_pct p-value: 3.087207035824368e-08
FFR_pct p-value: 2.073802964772698e-112):格兰杰因果检验:期货合约数据与联邦基金利率存在因果关系
Granger causality F-test.
H_0: futures_rate_pct does not Granger-cause FFR_pct.
Conclusion: reject H_0 at 5% significance level.
================================================
Test statistic Critical value p-value df
------------------------------------------------
41.03 1.460 0.000 (30, 8978)
------------------------------------------------3):方差分解:展示部分分解结果,滞后30期的期货合约数据对联邦基金利率波动率依旧解释了75.12%,很高。
FEVD for FFR_pct
FFR_pct futures_rate_pct
0 1.000000 0.000000
1 0.999509 0.000491
2 0.997702 0.002298
... ... ...
28 0.267247 0.732753
29 0.257543 0.742457
30 0.248806 0.7511944):脉冲响应分析:观察图七右上角子图,从方向上看,期货合约数据对联邦基金利率存在很强的同向关系;对比图六从力度上看,滞后期的期货合约数据对联邦基金利率有更强影响,且在25个滞后期内,冲击影响未见显著衰减。

图七:期货合约及联邦基金利率脉冲响应分析
小结:对比之前目标利率分析,从联邦基金利率数据因果分析结果看,期货合约对联邦基金利率有更强的因果关系,更高的波动率解释力度和更强的脉冲响应。
3.3.2 回归分析
使用期货滞后项对联邦基金利率进行回归,模型解释力度为0.481,对比之前的目标利率回归模型高了一倍多,解释力较强。回归系数约为0.76,也就是说今天如果观察到期货合约上升1个基点,未来联邦基金利率将上升0.76个基点。
futures["futures_rate_pct_leg"] = futures["futures_rate_pct"].shift(21)
futures.dropna(inplace=True)
model = smf.gls(data=futures, formula="FFR_pct~futures_rate_pct_leg")
result = model.fit()
print(result.summary())
GLS Regression Results
==============================================================================
Dep. Variable: FFR_pct R-squared: 0.481
Model: GLS Adj. R-squared: 0.480
Method: Least Squares F-statistic: 4196.
========================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------------
Intercept 0.0090 0.003 3.351 0.001 0.004 0.014
futures_rate_pct_leg 0.7604 0.012 64.779 0.000 0.737 0.783
========================================================================================
4. 实证检验结果
结合上面3.1及3.2的分析,笔者认为用期货合约数据来预测未来联邦基金利率是涨是跌有一定的参考意义的,而预测目标利率的效果差强人意。究其根本原因还是联邦基金目标利率是(糟)老头们定出来的。并且在前面笔者谈传导机制也介绍过了,这个目标利率是对联邦基金利率产生的间接影响,而期货合约的标的物为联邦基金利率。
用一句诗来做个不恰当的比喻:“此爱翻山海,山海亦可平;易平是山海,难平是人心”。用期货合约预测目标利率变就好比是“此爱翻山海”,各种数学工具各种上,总能算出点道道。但山海可平,真正难以预测的却是人心尔。
笔者也留意到一个很有意思的现象:公开市场操作委员会一年开八次会议,上面拟合出的最佳滞后项都为31,而笔者选取的期货数据是近月合约的滚动数据。也就是说318=248,将近就是一年的交易日数量,或许这不是巧合。
5. 总结
本文通过实证检验发现期货合约数据对联邦基金利率的解释力度,强于对公开市场委员会未来制定的目标利率的解释力度,这一现象极大削弱了基于期货合约预测未来加息/降息概率的准确度。笔者认为背后的根本原因是期货合约标的物差异导致的,因此不能单纯依靠期货合约预测未来加息/降息概率。此外,依靠期货合约进行预测另一个重要假设是市场有效性。而事实情况是期货市场往往呈现更大的波动和不确定性,这进一步使得预测的准确度大打折扣。
其实除了文章介绍的期货合约,还可以通过调查问卷或者其它多因子模型预测未来目标利率。笔者认为利用宏观数据解释目标利率将会比期货合约更有效,毕竟公开市场操作委员会的(糟)老头们是根据经济状况确定进行加/降息,而不是看期货数据。
本文研究有一定的局限性,受到数据制约,笔者没有研究远月合约的表现。其次,文中所使用的期货合约数据是连续滚动数据,与真实合约是存在微小差异的。本文主要目的是验证预测的可行性,笔者并没有对文章的回归模型进行验证测试。最后,笔者只是研究了现象及原理,并没有针对这种预测偏差验证其它改进的方案。
6. 参考文献
【1】美国联邦基金利息率的决定、传递机制和美联储升息的影响(来源:中国宏观经济论坛)
【2】CME group. (2023). 30 day federal fund futures overview. Chicago Mercantile Exchange. https://www.cmegroup.com/markets/interest-rates/stirs/30-day-federal-fund.html
【3】Keasler, TR. & Goff, DC. (2007). Using fed funds futures to predict a federal reserve Rate hike. Journal of Economics and Finance Education. 6(2). 9-14. Microsoft Word - KeaslerGoffpaper.doc (economics-finance.org)
【4】2023加息or降息,市场怎么看?(来源:东方财富网 )
7. 附录
1):期货数据及目标利率数据的VAR模型输出
Summary of Regression Results
==================================
Model: VAR
Method: OLS
Date: Wed, 26, Apr, 2023
Time: 23:06:07
--------------------------------------------------------------------
No. of Equations: 2.00000 BIC: -10.9263
Nobs: 4570.00 HQIC: -11.0411
Log likelihood: 12528.3 FPE: 1.50600e-05
AIC: -11.1035 Det(Omega_mle): 1.46532e-05
--------------------------------------------------------------------
Results for equation target_rate_pct
=======================================================================================
coefficient std. error t-stat prob
---------------------------------------------------------------------------------------
const 0.000578 0.000902 0.642 0.521
L1.target_rate_pct 0.980909 0.014894 65.857 0.000
L1.futures_rate_pct 0.021595 0.013943 1.549 0.121
L2.target_rate_pct -0.028824 0.020860 -1.382 0.167
L2.futures_rate_pct 0.015776 0.017053 0.925 0.355
L3.target_rate_pct -0.001561 0.020863 -0.075 0.940
L3.futures_rate_pct 0.101358 0.017358 5.839 0.000
L4.target_rate_pct 0.016094 0.020855 0.772 0.440
L4.futures_rate_pct -0.144865 0.017422 -8.315 0.000
L5.target_rate_pct -0.010413 0.020852 -0.499 0.618
L5.futures_rate_pct 0.027393 0.017565 1.559 0.119
L6.target_rate_pct -0.014229 0.020845 -0.683 0.495
L6.futures_rate_pct 0.059297 0.017571 3.375 0.001
L7.target_rate_pct 0.008696 0.020738 0.419 0.675
L7.futures_rate_pct -0.047612 0.017601 -2.705 0.007
L8.target_rate_pct -0.060947 0.020724 -2.941 0.003
L8.futures_rate_pct -0.014246 0.017621 -0.808 0.419
L9.target_rate_pct 0.019543 0.020680 0.945 0.345
L9.futures_rate_pct 0.018569 0.017362 1.070 0.285
L10.target_rate_pct 0.048286 0.019306 2.501 0.012
L10.futures_rate_pct 0.058742 0.017213 3.413 0.001
L11.target_rate_pct -0.024267 0.017991 -1.349 0.177
L11.futures_rate_pct -0.077882 0.016058 -4.850 0.000
L12.target_rate_pct -0.010395 0.018186 -0.572 0.568
L12.futures_rate_pct 0.333106 0.016078 20.718 0.000
L13.target_rate_pct -0.063640 0.018193 -3.498 0.000
L13.futures_rate_pct -0.223642 0.016832 -13.287 0.000
L14.target_rate_pct 0.052564 0.018231 2.883 0.004
L14.futures_rate_pct -0.039701 0.017166 -2.313 0.021
L15.target_rate_pct 0.037529 0.018246 2.057 0.040
L15.futures_rate_pct -0.018659 0.017179 -1.086 0.277
L16.target_rate_pct -0.010196 0.018242 -0.559 0.576
L16.futures_rate_pct -0.040523 0.017177 -2.359 0.018
L17.target_rate_pct -0.012852 0.018238 -0.705 0.481
L17.futures_rate_pct 0.016619 0.017187 0.967 0.334
L18.target_rate_pct 0.002770 0.018209 0.152 0.879
L18.futures_rate_pct -0.002759 0.017165 -0.161 0.872
L19.target_rate_pct 0.020638 0.017912 1.152 0.249
L19.futures_rate_pct 0.027595 0.017152 1.609 0.108
L20.target_rate_pct -0.024657 0.017353 -1.421 0.155
L20.futures_rate_pct 0.014537 0.017093 0.851 0.395
L21.target_rate_pct -0.444764 0.017306 -25.700 0.000
L21.futures_rate_pct -0.013237 0.016721 -0.792 0.429
L22.target_rate_pct 0.491549 0.018502 26.567 0.000
L22.futures_rate_pct -0.027155 0.017833 -1.523 0.128
L23.target_rate_pct -0.097967 0.019883 -4.927 0.000
L23.futures_rate_pct 0.071875 0.017950 4.004 0.000
L24.target_rate_pct 0.013898 0.019917 0.698 0.485
L24.futures_rate_pct 0.013989 0.018258 0.766 0.444
L25.target_rate_pct 0.012003 0.019911 0.603 0.547
L25.futures_rate_pct -0.129496 0.018249 -7.096 0.000
L26.target_rate_pct -0.006308 0.019878 -0.317 0.751
L26.futures_rate_pct 0.043441 0.018350 2.367 0.018
L27.target_rate_pct 0.009623 0.019874 0.484 0.628
L27.futures_rate_pct 0.029396 0.018360 1.601 0.109
L28.target_rate_pct 0.032615 0.019781 1.649 0.099
L28.futures_rate_pct 0.009009 0.018344 0.491 0.623
L29.target_rate_pct 0.010450 0.019634 0.532 0.595
L29.futures_rate_pct -0.020379 0.018344 -1.111 0.267
L30.target_rate_pct -0.029808 0.019632 -1.518 0.129
L30.futures_rate_pct 0.004578 0.018126 0.253 0.801
L31.target_rate_pct -0.018561 0.014079 -1.318 0.187
L31.futures_rate_pct 0.018382 0.014771 1.244 0.213
=======================================================================================
Results for equation futures_rate_pct
=======================================================================================
coefficient std. error t-stat prob
---------------------------------------------------------------------------------------
const 0.000748 0.000958 0.780 0.435
L1.target_rate_pct 0.016191 0.015832 1.023 0.306
L1.futures_rate_pct 0.706786 0.014820 47.690 0.000
L2.target_rate_pct 0.015992 0.022174 0.721 0.471
L2.futures_rate_pct 0.231550 0.018127 12.774 0.000
L3.target_rate_pct -0.002716 0.022177 -0.122 0.903
L3.futures_rate_pct 0.001536 0.018451 0.083 0.934
L4.target_rate_pct -0.006593 0.022168 -0.297 0.766
L4.futures_rate_pct 0.041821 0.018519 2.258 0.024
L5.target_rate_pct -0.013213 0.022164 -0.596 0.551
L5.futures_rate_pct -0.013993 0.018671 -0.749 0.454
L6.target_rate_pct -0.001508 0.022157 -0.068 0.946
L6.futures_rate_pct 0.042775 0.018677 2.290 0.022
L7.target_rate_pct 0.006720 0.022044 0.305 0.760
L7.futures_rate_pct -0.061141 0.018709 -3.268 0.001
L8.target_rate_pct -0.008928 0.022028 -0.405 0.685
L8.futures_rate_pct 0.015939 0.018730 0.851 0.395
L9.target_rate_pct -0.099098 0.021982 -4.508 0.000
L9.futures_rate_pct -0.007098 0.018455 -0.385 0.701
L10.target_rate_pct 0.033348 0.020521 1.625 0.104
L10.futures_rate_pct 0.028737 0.018297 1.571 0.116
L11.target_rate_pct 0.187480 0.019124 9.803 0.000
L11.futures_rate_pct -0.009582 0.017069 -0.561 0.575
L12.target_rate_pct -0.039108 0.019331 -2.023 0.043
L12.futures_rate_pct 0.055385 0.017091 3.241 0.001
L13.target_rate_pct -0.052684 0.019338 -2.724 0.006
L13.futures_rate_pct -0.050272 0.017892 -2.810 0.005
L14.target_rate_pct -0.003565 0.019379 -0.184 0.854
L14.futures_rate_pct -0.032002 0.018246 -1.754 0.079
L15.target_rate_pct 0.000844 0.019395 0.044 0.965
L15.futures_rate_pct 0.011163 0.018261 0.611 0.541
L16.target_rate_pct 0.000610 0.019391 0.031 0.975
L16.futures_rate_pct 0.011333 0.018259 0.621 0.535
L17.target_rate_pct -0.035641 0.019386 -1.839 0.066
L17.futures_rate_pct -0.006246 0.018269 -0.342 0.732
L18.target_rate_pct 0.018654 0.019355 0.964 0.335
L18.futures_rate_pct 0.000961 0.018245 0.053 0.958
L19.target_rate_pct 0.011758 0.019040 0.618 0.537
L19.futures_rate_pct 0.021875 0.018232 1.200 0.230
L20.target_rate_pct -0.003115 0.018445 -0.169 0.866
L20.futures_rate_pct 0.036489 0.018169 2.008 0.045
L21.target_rate_pct 0.020767 0.018396 1.129 0.259
L21.futures_rate_pct -0.448719 0.017774 -25.246 0.000
L22.target_rate_pct -0.011889 0.019667 -0.605 0.545
L22.futures_rate_pct 0.153675 0.018956 8.107 0.000
L23.target_rate_pct -0.015666 0.021135 -0.741 0.459
L23.futures_rate_pct 0.231594 0.019080 12.138 0.000
L24.target_rate_pct 0.032305 0.021171 1.526 0.127
L24.futures_rate_pct -0.032298 0.019408 -1.664 0.096
L25.target_rate_pct -0.001739 0.021165 -0.082 0.935
L25.futures_rate_pct 0.012924 0.019398 0.666 0.505
L26.target_rate_pct -0.002617 0.021130 -0.124 0.901
L26.futures_rate_pct -0.008542 0.019505 -0.438 0.661
L27.target_rate_pct 0.000862 0.021125 0.041 0.967
L27.futures_rate_pct 0.018338 0.019516 0.940 0.347
L28.target_rate_pct 0.006693 0.021026 0.318 0.750
L28.futures_rate_pct -0.010886 0.019498 -0.558 0.577
L29.target_rate_pct 0.009597 0.020870 0.460 0.646
L29.futures_rate_pct 0.001172 0.019499 0.060 0.952
L30.target_rate_pct -0.122479 0.020868 -5.869 0.000
L30.futures_rate_pct -0.008034 0.019267 -0.417 0.677
L31.target_rate_pct 0.104183 0.014966 6.961 0.000
L31.futures_rate_pct -0.006720 0.015701 -0.428 0.669
=======================================================================================2):期货数据及目标利率数据的方差分解
FEVD for target_rate_pct
target_rate_pct futures_rate_pct
0 1.000000 0.000000
1 0.999732 0.000268
2 0.998731 0.001269
3 0.989180 0.010820
4 0.986945 0.013055
5 0.984171 0.015829
6 0.977735 0.022265
7 0.971963 0.028037
8 0.966838 0.033162
9 0.960710 0.039290
10 0.950480 0.049520
11 0.943252 0.056748
12 0.902592 0.097408
13 0.865871 0.134129
14 0.830866 0.169134
15 0.800353 0.199647
16 0.775632 0.224368
17 0.753577 0.246423
18 0.733287 0.266713
19 0.714546 0.285454
20 0.696616 0.303384
21 0.679408 0.320592
22 0.664439 0.335561
23 0.649009 0.350991
24 0.637003 0.362997
25 0.628720 0.371280
26 0.621284 0.378716
27 0.615759 0.384241
28 0.609921 0.390079
29 0.604263 0.395737
30 0.599277 0.400723
FEVD for futures_rate_pct
target_rate_pct futures_rate_pct
0 0.000657 0.999343
1 0.001179 0.998821
2 0.002604 0.997396
3 0.004430 0.995570
4 0.006260 0.993740
5 0.007586 0.992414
6 0.008600 0.991400
7 0.009821 0.990179
8 0.010722 0.989278
9 0.009935 0.990065
10 0.009506 0.990494
11 0.010302 0.989698
12 0.012678 0.987322
13 0.015043 0.984957
14 0.017467 0.982533
15 0.020114 0.979886
16 0.023095 0.976905
17 0.025354 0.974646
18 0.027774 0.972226
19 0.030014 0.969986
20 0.031812 0.968188
21 0.035182 0.964818
22 0.038533 0.961467
23 0.040985 0.959015
24 0.043384 0.956616
25 0.045702 0.954298
26 0.048485 0.951515
27 0.051713 0.948287
28 0.055139 0.944861
29 0.059175 0.940825
30 0.062910 0.937090
8. 系列精选
| 往期精选 | ||
| 系列 | 文章传送门 | 实现方式 |
| 基本面分析 | 实现GGM的理想国 | Python |
| PB指标与剩余收益估值 | Python | |
| Fama-French及PSM | Python | |
| GK模型看投资的本质 | Python | |
| 增速g的测算 | Python | |
| PE指标平滑 | Python | |
| PE Band | Python | |
| 技术分析 | 分类树算法 | R |
| 蒙特卡洛模拟 | Python | |
| 全连接神经网络模型 | Python | |
| 组合管理 | 券商金股哪家强——信息比率 | Python |
| 从指数构建原理看待A股的三千点魔咒 | Python | |
| 决策树学习基金持仓并识别公司风格类型 | R | |
| 杂谈类 | 垃圾公司对回报率计算的影响几何 | Python |
| 市场风险分析 | Python | |
| 金融危机模拟 | Python | |
您若不弃,我们风雨共济:)








![[架构之路-176]-《软考-系统分析师》-1-嵌入式系统分析与设计 - 实时性(任务切换时间、中断延迟时间、中断响应时间)、可靠性、功耗、体积、成本](https://img-blog.csdnimg.cn/4273303146bb413ea9ef10879cd6ede1.png)