这一章是数字图像处理基础的最后一章。系统的介绍傅里叶级数、傅里叶变换、离散傅里叶变换,快速傅里叶变换,以及二维傅里叶变换在图像上的应用。
变换的作用

首先我们先来聊聊什么是“变换”?其实在第一章介绍 HSI 颜色模型的时候,我们就用到了变换这一概念。所谓的变换其实就是把同一个物体事件,转换成另外一种形式表达,其过程相互可逆。傅里叶变换也是一样的,为了有效快速对信号中包含的高频/低频分量进行区分的处理,常常需要将原来定义在时域空间的信号,转换成频率域进行加工处理,然后再转换回时域呈现结果。
傅里叶级数
了解变换的作用之后,我们正式介绍第一个概念——傅里叶级数:任何 周期函数 都可以表示为 不同频率 的正弦波sin或者余弦波cos之和的形式,每个正弦项和余弦项都乘以不用的系数。关键在于如何找到sin和cos对应的系数。
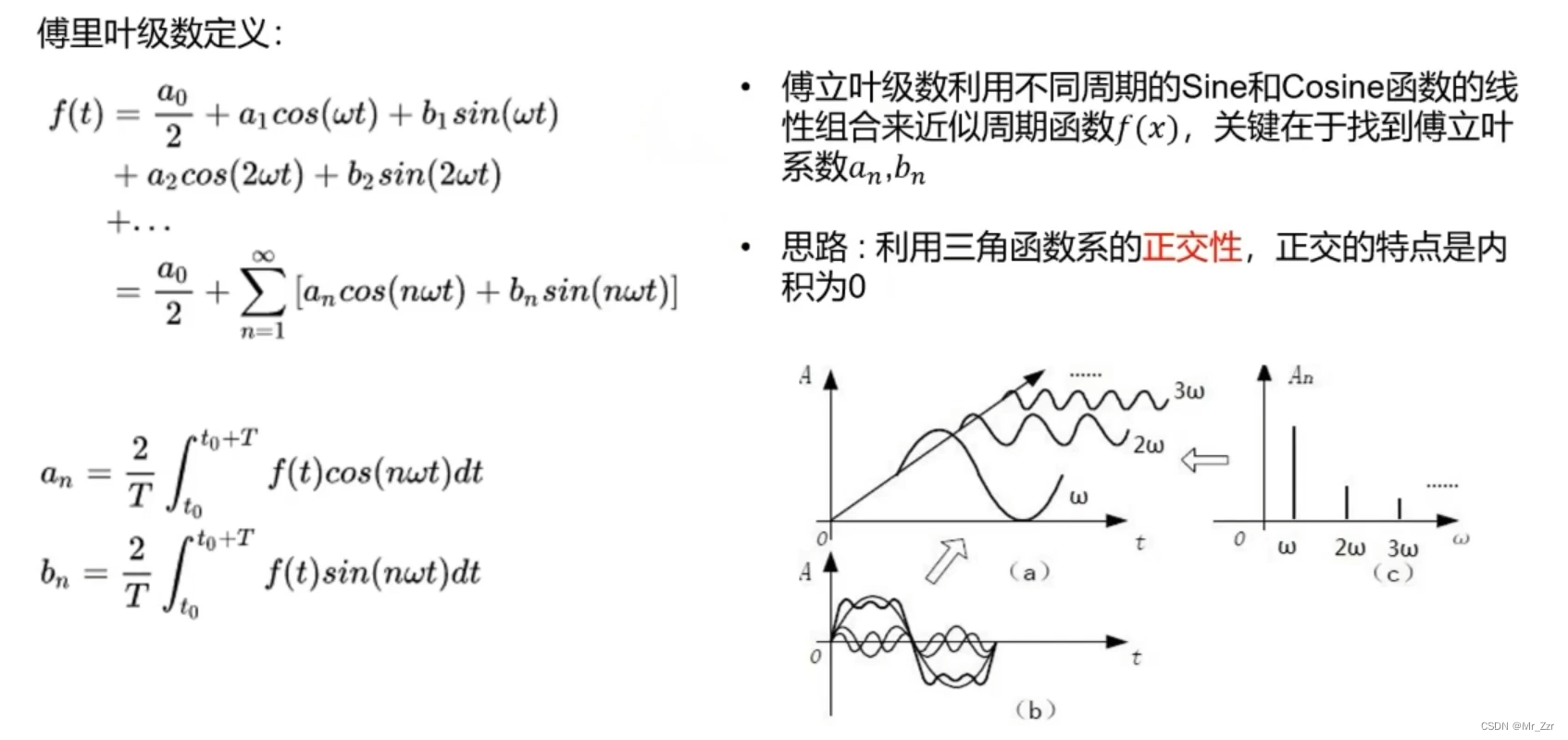
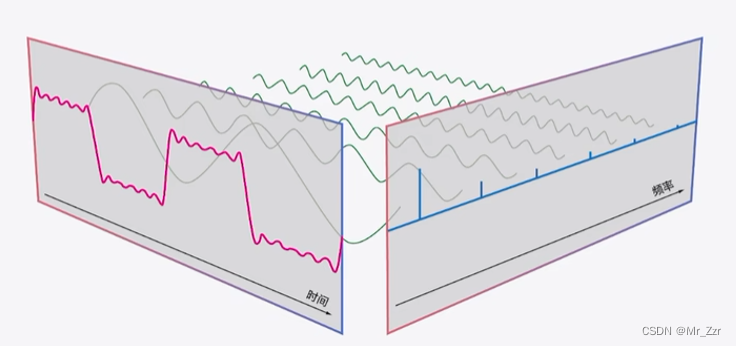
以上图示为傅里叶级数的数学定义。其实就是用数学的公式表示其定义,从右边的三个小图abc,图b是一个时域图(横坐标是t)它可以看成是由图a里面三个不同频率的信号叠加而成,而图c就是图a的频谱变换图,以频率为横坐标,振幅为纵坐标。由此可以总结,傅里叶级数由两个关键内容组成:
- 我们可以知道原始输入信号里包含了多少种不同频率ω的分信号。
- 还可以知道每一个频率下的对应的振幅A有多大。
那么为什么傅里叶级数是成立的呢?或者是说,为什么 周期函数 都可以表示为 不同频率 的正弦波sin或者余弦波cos之和的形式?其实这里是利用了三角函数函数的正交性特性。什么是正交性,举例子说:单位向量A1自己乘以自己的时候结果是1(内积 A1·A1=1),两个互相垂直的单位向量A1·A2 = 0,那么A1和A2相互正交,A1和A2称为标准正交基。利用这一特性,如果原始输入的周期函数具有频率ω成分,那么单独使用频率ω的正余弦波相乘,就会剩余频率ω分量的波形(A1·A1=1),滤去其他波形(A1·A2= 0)。
傅里叶变换
那么傅里叶级数好似只能处理 周期性函数,现实上大部分的信号都应该是属于非周期的,那么非周期函数它就没折了是不?由此我们正式介绍傅里叶变换,或者严谨点的说法叫 连续傅里叶变换。为了说明傅里叶变换,我们需要从另外一个公式说起,欧拉公式。

在复变函数中,e^(iθ)=(cosθ + i·sinθ) 称为欧拉公式,e是自然对数,i 是虚数的单位。也可以参考上图,横坐标为自然数的单位1,纵坐标为虚数的单位 i,那么任意圆上点A,它的横坐标就是cosθ乘以单位1,纵坐标就是sinθ乘以单位i,所以A可以写作(1·cosθ,i·sinθ)也可以写成A = cosθ + i·sinθ。如果我们把θ写成 θ = ω · t,ω为频率t为时间,那么顺着时间t的变大,A点绕着这个圆圈在逆时针的转动,那么欧拉公式与时间t三维展开就会呈现一种类似弹簧被拉长的画面,如下图所示。

那么欧拉公式
e^(iθ) = e^(i·ω·t) = (cos ω·t + i·sin ω·t)
代表随着时间 t 变化,e^(i·ω·t) 每时每刻都可以由一组正交基组合来表达。有了这个公式成立之后,我们就可以对一个非周期函数进行傅里叶变换了。对于一个非周期函数,可以看作成是一个周期无穷大的周期函数,按照傅里叶级数展开,也是可以分成很多个不同频率的信号,那么我们如何去分别开呢。
根据三角函数标注正交基的含义,频率ω的正弦信号,用sin(ω·t)去相乘就可以提取出来,而其他非ω信号就会全变成0。所以我们就可以在时间 t 的 [-∞, +∞]范围内,对信号乘以 e^(i·ω·t),写成积分的形式就是以下公式:
F(t) = ∫ [-∞, +∞] f(t) · e^(i·ω·t) dt(ω≠0)
利用欧拉公式可以转变成
F(t) = ∫ [-∞, +∞] f(t) · (cos ωt+i·sin ωt) dt
对应的复数形式就是
Fourier·Transform = ∫ [-∞, +∞] f(t)·(cos ωt) dt - i·∫ [-∞, +∞] f(t)·(sin ωt) dt
(注意后边的复数 i 部分从时间t积分中提取,复数内积后取负号)
根据三角函数标注正交基的含义,以上公式求解释式就分成两个:当含有频率为ω的信号时候,结果不为0,当不含有频率为ω的信号时候,结果为0。以上公式就可以称为 信号 f(t) 的傅里叶变换F(ω),这和傅里叶级数又有什么关系了?显然傅里叶级数可以利用欧拉公式变换成只有一个级数Cn和自然对数e的i·ω·t次幂的写法,即f(x) = ∫ [-∞, +∞] Cn·e^(i·ω·t) dt
从公式上可以了解到,傅里叶级数的频谱是不连续的数学代数表示,而傅里叶变换的是随时间而连续的函数表示。
离散傅里叶变换
上面介绍的连续傅里叶变换从理论上处理了自然界中的信号波,但是在计算机中只能处理离散的数字信号。所以说我们需要对模拟信号进行数字化采样,这就离不开奈奎斯特采样定理。简单来说就是用模拟信号中最长周期的2倍的采样率进行采样,才能准确把模拟信号数字化。
而且在傅里叶变换当中,时域和频域都是被看作周期无限长的序列。无限长序列在计算机运算仍然是无法实现。为此必须取有限长序列来建立其时域离散和频域离散的对应关系。基于以上这两点,离散傅里叶变换正式登场。
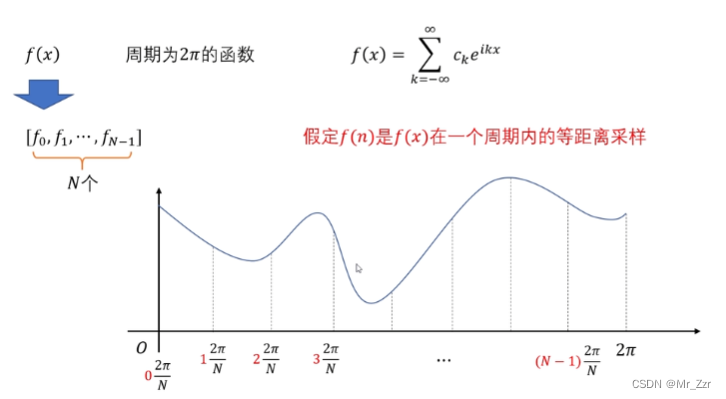
现实普遍的情况是,一个连续的周期函数f(x),用傅里叶级数表示法就是
f(x) = ∑(-∞,+∞) Ck·e^(i·k·x)
现将其进行数字化进行等距离采样,得出N个采样点f(0 ~ N-1)通过这N个采样点,如何确定傅里叶级数Ck?显然如果只提供N个采样点,那是没有办法找出所有的Ck,需要提供满足奈奎斯特采样定理的一个完整周期的采样点,才能找出所有的Ck,但是傅里叶是一个无限长周期函数,更不可能提供无限多个采样点,那怎么办?这个就是离散傅里叶变换面对的一个问题。
我们可以假设(N为采样点个数,n为具体采样序号,T为周期)已提供可知的这N个f(n)采样点,看作是一个周期内T=2Pi的 f(x) 的所有函数值,在这一个周期内的这N个点的坐标就已知,可以写成 n·2Pi / N(如上图示)需要注意的是,按照假设这N个点(n∈0 ~ N-1)是不包含 t 取 2Pi 的f(x)值,它是下一个周期的开始点,也就是说 t 取0*T的f(x)值应该等于 t 取1*T的f(x)值(周期函数收敛)
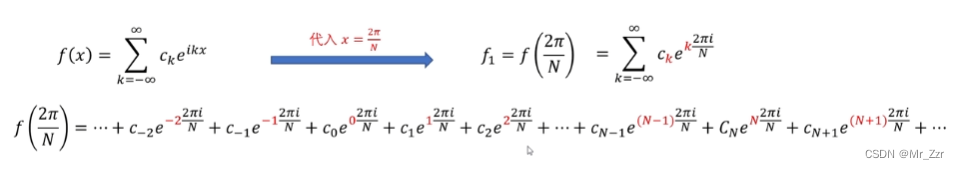
那么时域取 n = 1 的 x 值 1*2Pi / N,代入 f(x) 其傅里叶级数展开的如上图所示,红色的取值,就是傅里叶级数下标k从(-∞,+∞) 的取值(注意区分时域的采样点n∈[0 ~ N-1])。为了描述方便,我们设定 w = e^(i·2Π / N)
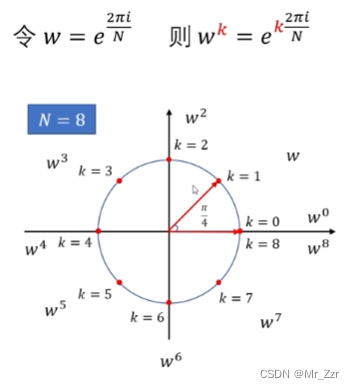
那么还记得傅里叶变换当中的欧拉圆?原来假设的在一个周期范围内的采样个数N=8,在(-∞,+∞) 范围内的傅里叶变换中的频域,傅里叶级数 k 也符合其周期性的特性!有了这个特性我们其实可以把无限个傅里叶级数进行简单的合并同类项,最后合并成k=8项的傅里叶级数和。那么离散傅里叶变换的问就变成了求解这N个基的加权系数,不再需要针对无限个傅里叶级数了。

我们再继续研究离散傅里叶级数的权重系数还有什么特性。取 n = 2 的 x 值 2*2Pi / N。我们利用上方给定的 w = e^(i·2Π / N) 进行简写。
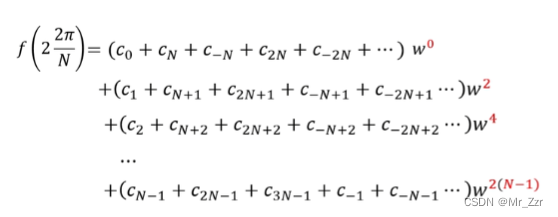
对比取 n = 1 的 x 值 1*2Pi / N。其傅里叶级数的权重系数是一致的,但是 w 变为原来的n次方,而且超出范围的 w^2(N-1)次幂也不用害怕,从上面分析得出的结论“傅里叶级数 k 也符合其周期性的特性”也是可以求出 w^2(N-1)次幂也就等于w^(N-1)。 也就是说,这N个f(n)采样值都可以用 w^1,w^2,w^3,……w^(N-1)这N个傅里叶级数和来表示。
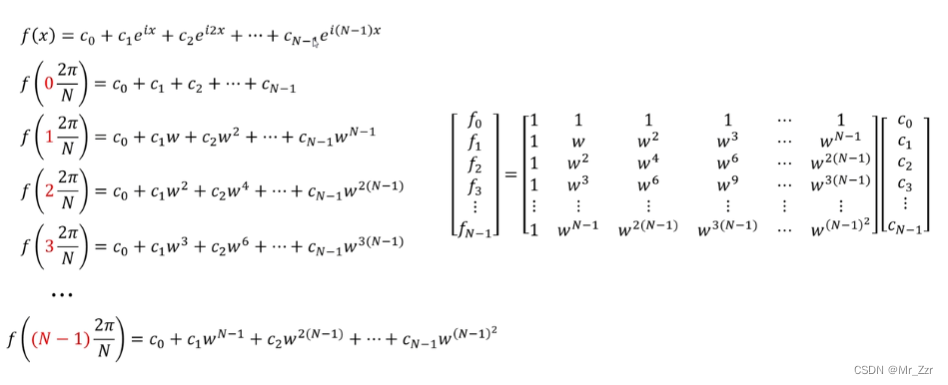
接下来就很关键了,N是采集个数,f(n)是采样值(n∈[0 ~ N-1]),都是可知的,那么w^1,w^2,w^3,……w^(N-1)也是可求的。那么f(n)和w^1,w^2,w^3,……w^(N-1)就可以写出N个N元一次方程。那是不是就可以矩阵求解?上一章才聊完的最小二乘法矩阵求解,这个比最小二乘还简单,只需要一个求逆就可以算出Ck的矩阵了。
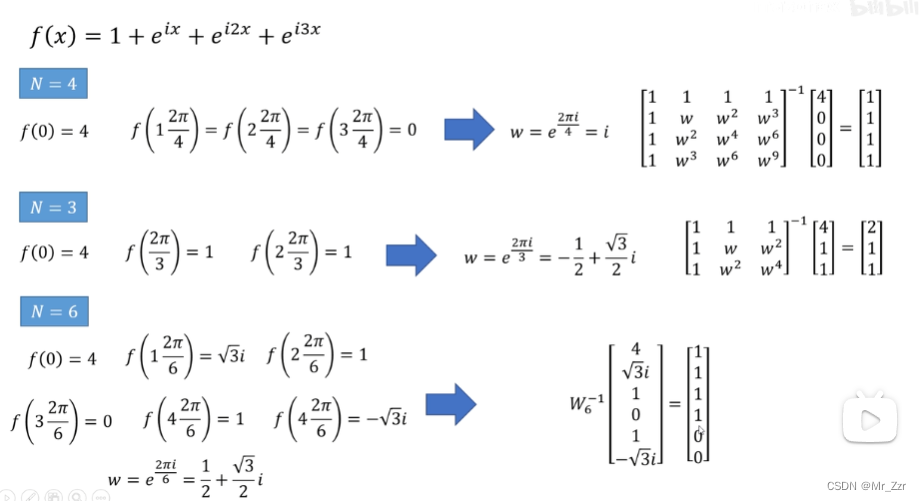
还需要注意的是,如果采样点大于或小于原函数的真正周期,傅里叶级数矩阵会有什么表现呢?其实从上面分析的,组成 w 基权重的傅里叶级数和,我们可以稍微的知道,以w⁰为例,他的权重是(C0+CN +C-N +C2N +C-2N +···)谈若采样个数小于真实周期,那么我们就会误把下个周期的傅里叶级数增加进来。
上面是一个具体的例子,f(x) = 1 + e^ix + e^i2x + e^i3x,级数有4个分别都是1,如果采样个数N=3,那离散傅里叶就会把周期当成3,把C(0+T)当成CN,进而导致傅里叶矩阵的第一个解析解为2,但随着采样个数的增大,这个错误解会得到及时的纠正。
下一章我们探讨快速傅里叶变换 和 傅里叶变换在二维图像上的应用。