【单目标优化算法】杂草优化算法（Matlab代码实现）

news2024/9/21 2:33:31

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

杂草算法代码简单，易于实现，具有较强的自适应性和鲁棒性。

算法步骤：(以搜索最小值为例)

1、初始化种群

随机生成一定数量的初始解(杂草)，这些初始解(杂草)随机地均匀地分布在搜索空间(草原)内。

2、种群繁殖

现实世界中，不同杂草在草原上的适应度不同，适应度高的个体生长旺盛，将会产生更多的子代种子。

对应到最优解搜索问题中，接近最优解的解具有更强的适应度，会产生更多的子代个体(下一代的解)。远离最优解的解具有较低适应度，会产生较少的下一代个体。

基于上述分析，当前解产生子代种子个数公式如下：

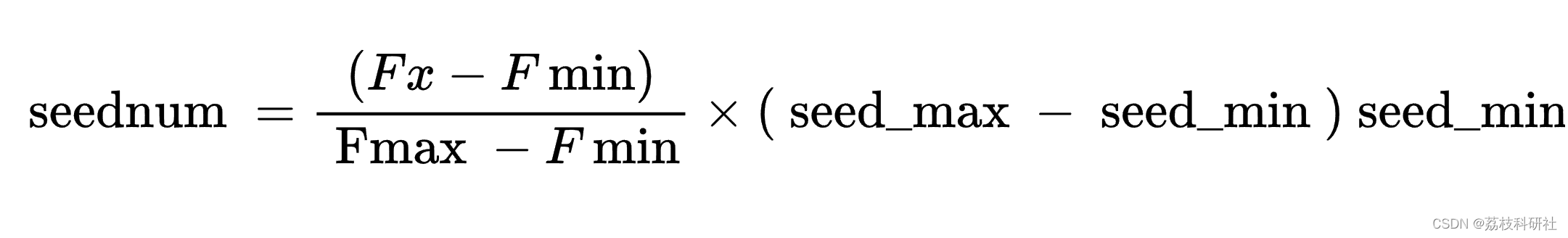
其中，Fx代表当前解的适应度，Fmin代表当前种群中所有解的最小适应度，Fmax代表代表当前种群中所有解的最大适应度。seed_max和seed_min分别代表每次迭代过程中单个解能够随机生成的最大/最小种子个数。

注意，当搜索目标函数最大解时，

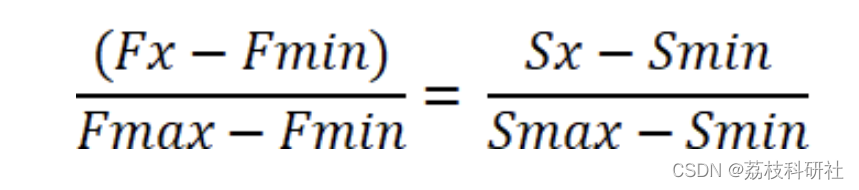
当搜索目标函数最小解时，

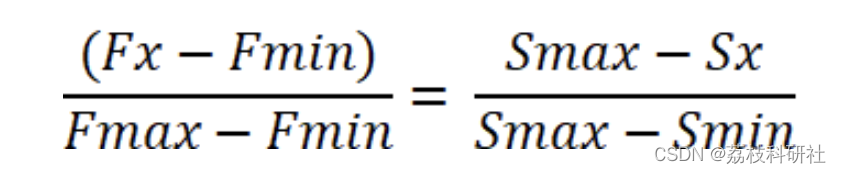
其中Smax代表当前种群目标函数最大值，Smin代表当前种群目标函数最小值。(当搜索最小值的时候，函数值最小的解适应度最大)

3、空间搜索

现实世界中，杂草的种子随着动物的运动、风能等传播到父代个体周围。种子传播的距离服从正态分布。

对应到最优解搜索过程中，当前解的子代服从正态分布，该正态分布的均值为当前解的位置，标准差定义为sigma，sigma随着时间的推移与当前迭代次数g成负相关，在sigma最大值sigma_max、sigma最小值sigma_min、最大迭代次数g_max以及非线性调节因子w给定的情况下：

$\text { sigma }=\operatorname{sigma}_{\min }+\left(\frac{g_{\max }-g}{g_{\max }}\right)^{w} \times\left(\operatorname{sigma}_{\max }-\operatorname{sigma}_{\min }\right)$

📚2 运行结果

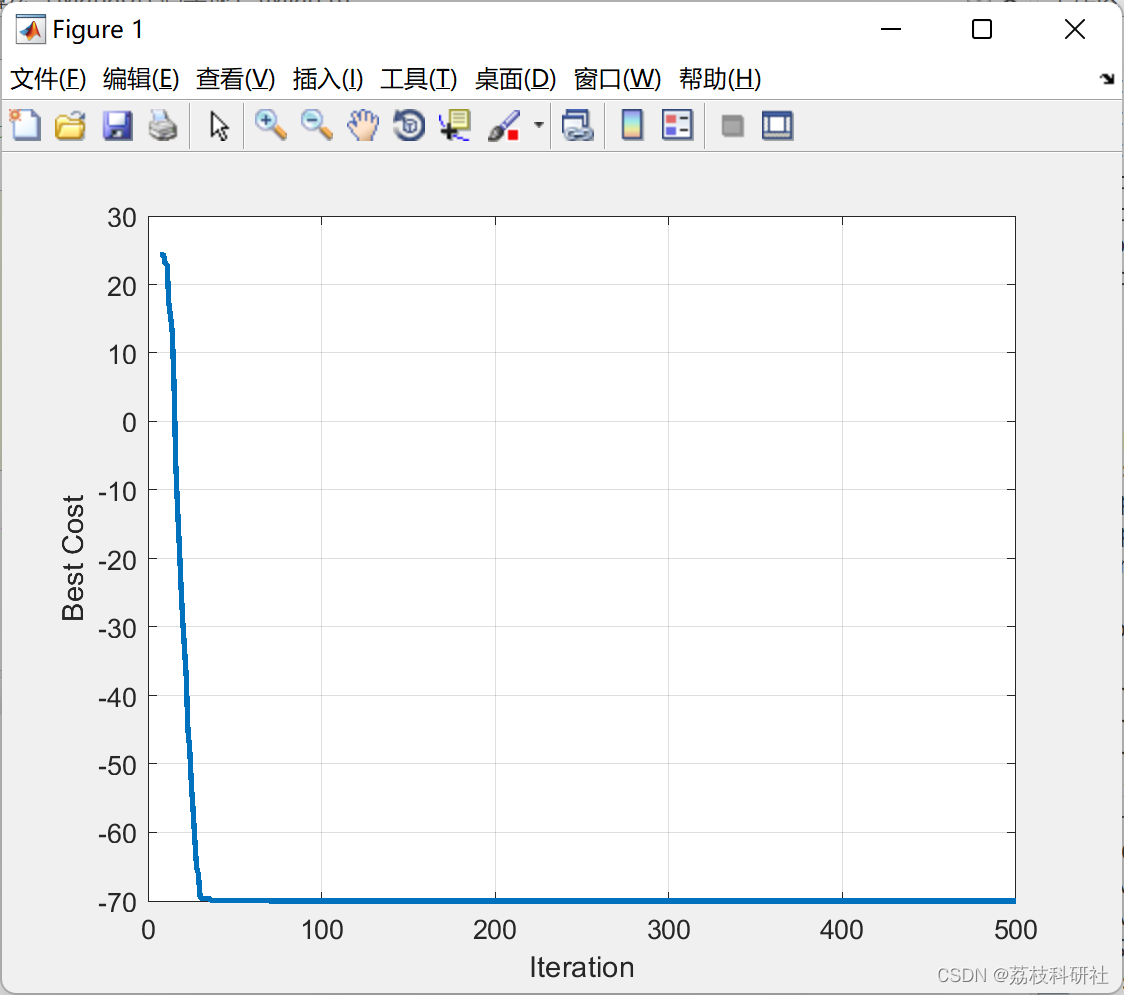
部分代码：

%% IWO Main Loop
for it = 1:MaxIt
% 更新标准偏差
sigma = ((MaxIt - it)/(MaxIt - 1))^Exponent * (sigma_initial - sigma_final) + sigma_final;
% 获得最佳和最差的目标值
Costs = [pop.Cost];
BestCost = min(Costs);
WorstCost = max(Costs);
% 初始化子代种群
newpop = [];
% 繁殖
for i = 1:numel(pop)
% 比例系数
ratio = (pop(i).Cost - WorstCost)/(BestCost - WorstCost);
% 每个杂草产生的种子数
S = floor(Smin + (Smax - Smin)*ratio);
for j = 1:S
% 初始化子代
newsol = empty_plant;
% 生成随机位置
% randn是一种产生标准正态分布的随机数或矩阵的函数
newsol.Position = pop(i).Position + sigma * randn(VarSize);
% 边界(下限/上限)处理
newsol.Position = max(newsol.Position, VarMin);
newsol.Position = min(newsol.Position, VarMax);
% 子代的目标函数值
newsol.Cost = CostFunction(newsol.Position);
% 添加子代
newpop = [newpop;
newsol]; % #ok
end
end
% 合并种群
pop = [pop;
newpop];
% 种群排序
[~, SortOrder] = sort([pop.Cost]);
pop = pop(SortOrder);
% 竞争排除（删除额外成员）
if numel(pop)>nPop
pop = pop(1:nPop);
end
% 保存最佳种群
BestSol = pop(1);
% 保存最优函数值历史记录
BestCosts(it) = BestSol.Cost;
% 显示迭代信息
% disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCosts(it))]);
end