背包问题
01背包问题
有N个·物品和容量是V的背包,每个物品有价值vi和权重(价值)wi属性,每件物品只能用一次(要么用0次,要么用1次),在背包能装得下的情况下,挑一部分物品装入背包,怎样挑才能保证这些物品的价值最大。
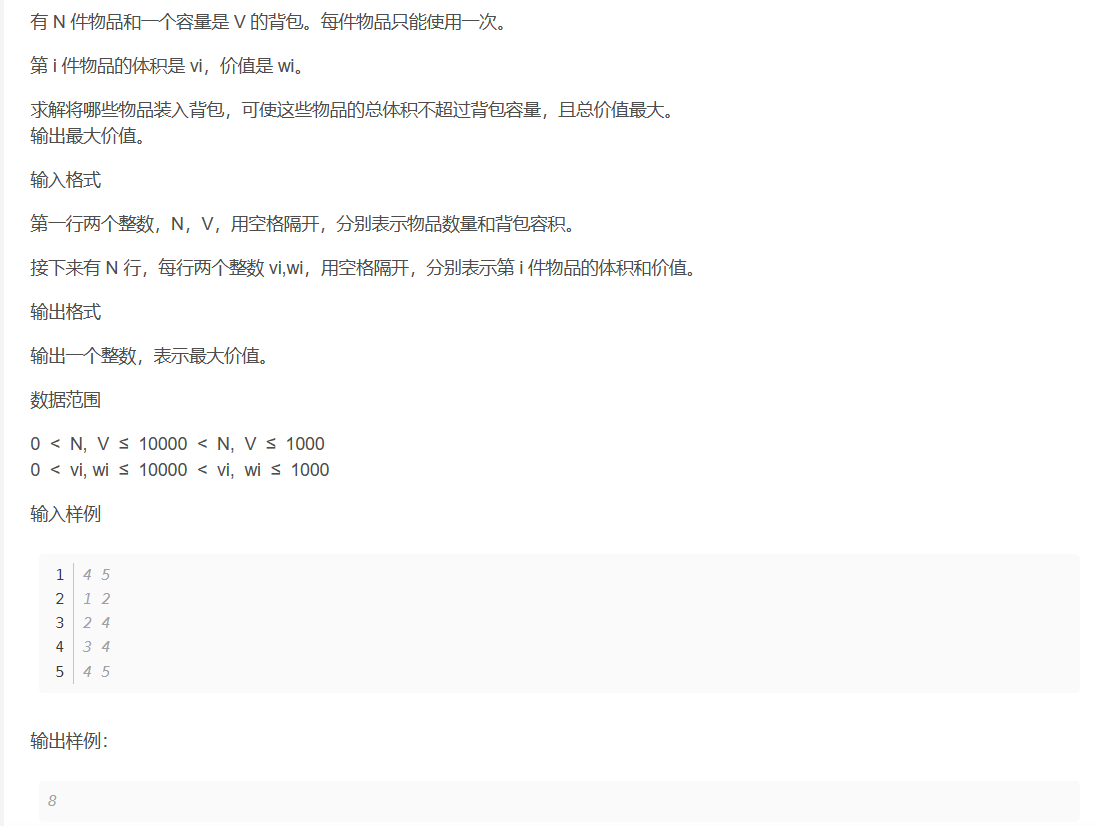
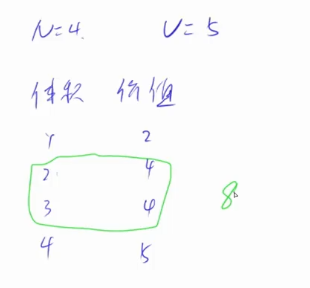
f(i,j)集合表示所有选法里面的最大值

f(N,V)表示从前N个物品选,总体积不超过V的集合,状态计算表示的是集合的划分,状态计算是把当前的集合表示成更小的子集,即把当前状态用前面更小的状态表示出来,我们这里采用把f(i,j)所有的选法表示成俩大类,以含i和不含i为划分标准。
划分原则:
这里划分的时候要做到不重复,即某一个元素不能属于俩个集合,只能属于其中一个。
不漏,不能漏掉任何一个小的元素(不能让某个元素不属于任何一个集合)
不漏一定要满足,但是不重有时候可以不用满足。
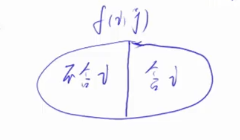
左边的集合的特点是从1到i-1中选,并且总体积不超过j。用f(i-1.j)表示.
右边集合的特点是所有从1到i中选,总体积不超过j,可以包含i。
步骤:
右边的选法里面都包含第i个物品,我们在选择的时候先把每种选法里面的第i个物品都去掉,这个不会影响最大值。
右边也变成了从i到i-1中选,由于没去掉第i个物品时,总体积不超过j,去掉了第i个物品后,总体积不超过j-vi。右边变成f(i-1,j-vi)
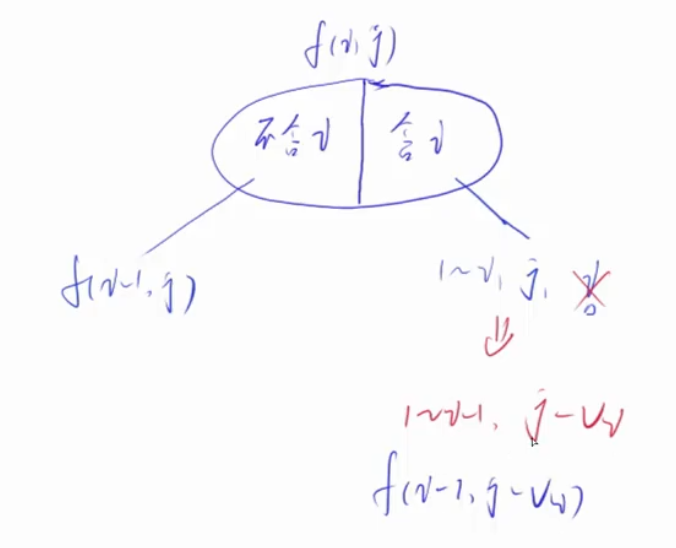
选完之后,我们把第i个物品再加回来,右边这种情况的最大价值是f(i-1,j-vi)+wi
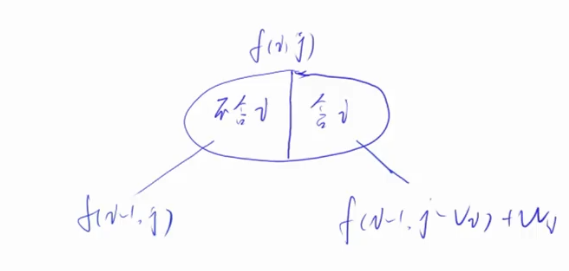
我们最后将左边和右边价值相比较,取最大值即可
注意左边集合的这种情况是一定存在的,右边这种情况不一定存在,可能会是空集,当背包体积小于右边vi的时候就是空集。
二维表示
#include<iostream>
#include<algorithm>
using namespace std;
// 01背包问题
const int N = 1010;
int n, m;//n表示物品个数,m表示背包容量
int v[N], w[N];//V表示体积,w表示价值
int f[N][N]; //表示状态
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
//初始化的时候 要计算所有的状态,f[0~n][0~m]是所有的状态
//f[0][0~m]表示0件物品,总体积不超过0,价值0~m,这样的情况下最大价值是多少,由于一件物品都没选,所以它是0,由于数组会默认是0,我们就不需要初始化
//因此我们从1开始枚举
for (int i = 1; i <= n; ++i)
{
for (int j = 0; j <= m; j++)
{
f[i][j] = f[i - 1][j];//左边这种情况是存在的
if (j >= v[i])//右边这种情况不一定存在
f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
}
cout << f[n][m] << endl;
return 0;
}一维表示
int f[N];
const int N = 1010;
int n, m;//n表示物品个数,m表示背包容量
int v[N], w[N];//V表示体积,w表示价值
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
//初始化的时候 要计算所有的状态,f[0~n][0~m]是所有的状态
//f[0][0~m]表示0件物品,总体积不超过0,价值0~m,这样的情况下最大价值是多少,由于一件物品都没选,所以它是0,由于数组会默认是0,我们就不需要初始化
//因此我们从1开始枚举
for (int i = 1; i <= n; ++i)
{
for (int j = m; j >= v[i]; j--)//一维数组表示的时候,j从0到vi-1的时候是没有意义的,因为下面有这个判断,
//所以我们直接从m开始,然后这个判断也可以不要
//从m开始的另一个原因,要保证出现跟f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);一样的效果
{
//if (j >= v[i])//右边这种情况不一定存在
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
cout << f[m] << endl;
return 0;
}完全背包问题
每件物品有无限个。
状态计算和01背包问题有所不同,完全背包问题,状态计算表示的是集合的划分。
该集合表示的是第i个物品选0个,第i个物品选1个,第i个物品选2个,第i个物品选3个,第i个物品选4个……一直到k个,要注意背包的容量,这里最多选K个。
f[i,j]表示前i个物品,总体积不超过j。
0这个子集表示第i个物品不选。等价于只考虑选前i-1个物品,并且总体积不超过j。
用f[i-1,j]来表示。
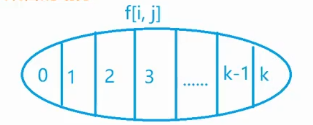
我们现在考虑选前i个物品,并且第i个物品选了K个这样选法的集合。
步骤:
去掉k个物品i,即去掉k个第i个物品
求max,由于去掉了k个第i个物品,现在变成了max=f[i-1,j-k*v[i]]
再把去掉的加回来,即+k个物品i
f[i-1,j-k*v[i]]+k*w[i]
f[i,j]=f[i-1,j-v[i]*k]+w[i]*k。
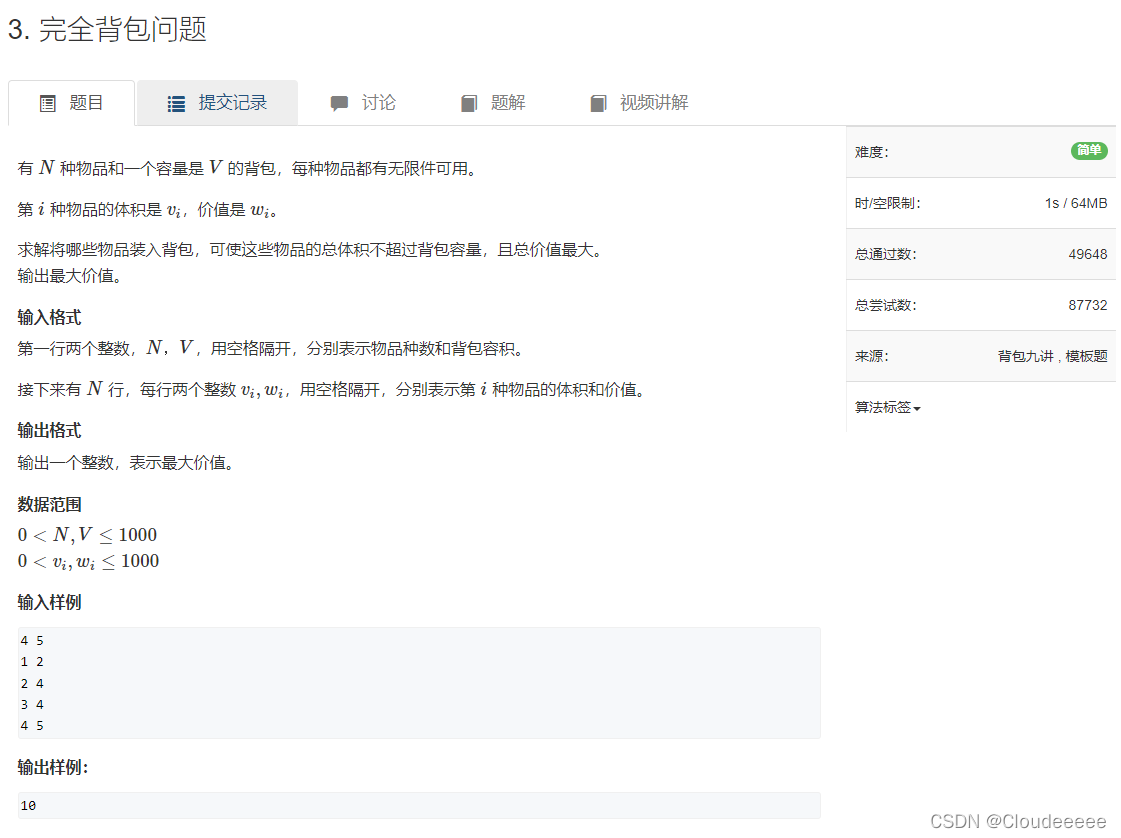
朴素算法
const int N = 1010;
int n, m;
int v[N],w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i++)//枚举所有状态
for (int j = 0; j <= m; ++j)
for (int k = 0; k * v[i] <= j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - v[i]*k] + k * w[i]);
cout << f[n][m] << endl;
return 0;
}优化二维算法
把下列式子展开
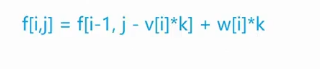
橙色部分比红色部分的每一项都多了W

我们再枚举的时候,枚举俩个状态就可以了,第二个状态在体积满足条件的情况下才可以使用
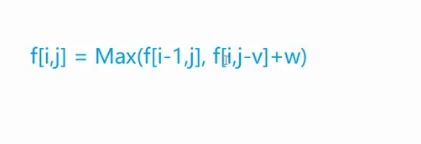
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i++)//枚举所有状态
for(int j=0;j<=m;j++)
{
f[i][j] = f[i - 1][j];
if (j >= v[i])
f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}优化一维算法
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; ++i) cin >> v[i] >> w[i];
for (int i = 1; i <= n; i++)//枚举所有状态
for(int j=v[i];j<=m;j++)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] << endl;
return 0;
}多重背包问题1
多重背包问题,每件物品的个数是有限制的。
跟完全背包相似,根据第i个物品选多少个,把第i个物品分成若干种类
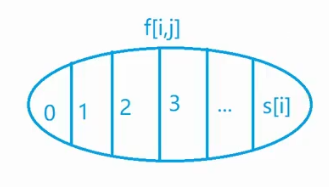
状态转移方程跟完全背包的朴素算法一样
k从0,1,2一直到s[i]

const int N = 110;
int n, m;
int v[N], w[N], s[N];
int f[N][N];
int main()
{
cin >> n >>m;
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++)
for (int k = 0; k <= s[i] && k * v[i] <= j; k++)//注意这里的体积范围,总共需要的体积小于等于给定的体积
f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);
cout << f[n][m] << endl;
return 0;
}多重背包问题2
跟多重背包问题1相比,数据范围变大了,如果直接按多重背包问题1去做,会超时。
我们发现f[i,j-v]后面多了一项。因此,我们不能直接用完全背包的优化方式,来优化这道题

这里采用二进制的优化方式。
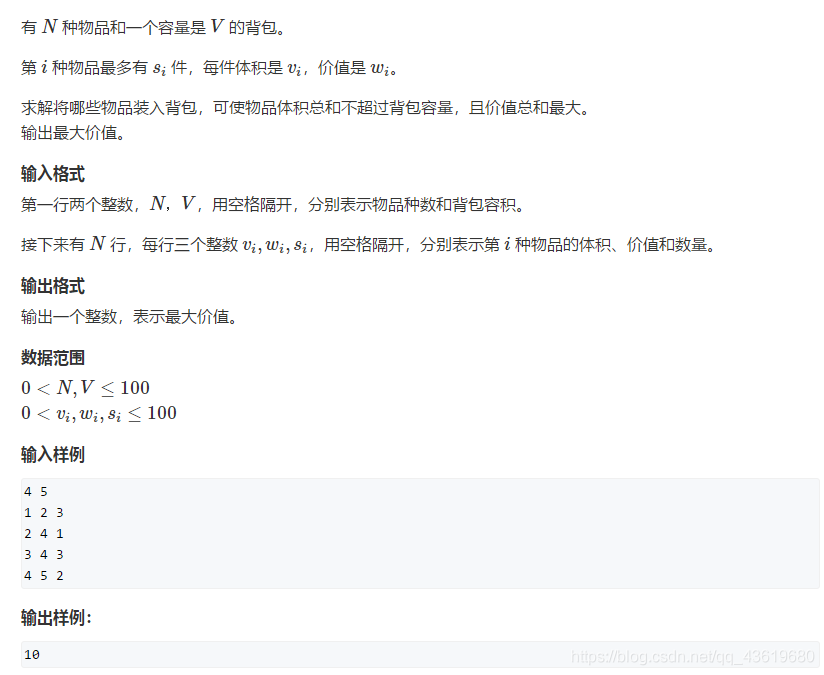
假设某个物品有1023个,s=1023,我们不需要从0枚举到1023,我们可以先把若干个第i个物品打包在一块来考虑,1,2,4,8……512分别代表第一组,第二组,第三组有1,2,4个i物品,即把i物品打包成10组,最多从每组中选1个,然后从选出来的这10个中平凑出0-1023中的任何一个数。
当s=200,我们可以这样打包,最后一组是73,分组规则按照以2为底的质数进行增长,但所有组数加一起的和不能超过某个数的总个数。
第i个物品有s个,我们可以拆分成新的logs组新的物品,新的物品只能用一次。

步骤:
先把第i个物品拆分
对拆分出来的新的物品,做一遍01背包即可
时间复杂度为


const int N = 25000, M = 2010;
int n,m;
int v[N], w[N];
int f[N];
int main()
{
cin >>n >>m;
int cnt = 0;//表示所有新的物品
for (int i = 1; i <= n; i++)
{
int a, b, s;//当前物品的体积,价值,个数
cin >> a >> b >> s;
int k = 1;//从1开始分
while (k<=s)
{
cnt++;//新物品的编号++
v[cnt] = a * k;//体积
w[cnt] = b * k;//价值
s -= k;
k *= 2;
}
if (s > 0)//此时剩下一些需要补上
{
cnt++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt;//分组完成
//做01背包问题即可
for (int i = 1; i <= n; ++i)
for (int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
cout << f[m] <<endl;
return 0;
}
分组背包问题
枚举第i组物品,选哪个。
从左到右分别是第i组物品选第0个,第i组物品选第1个……第i组物品选第n个。
从第i组物品选第k个
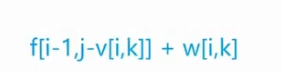

const int N =110 ;
int n, m;
int v[N][N], w[N][N],s[N];//s存每一组的个数
int f[N];
int main()
{
cin >> n >>m;
for (int i = 1; i <= n; i++)
{
cin >> s[i];
for (int j = 0; j < s[i]; j++)
cin >> v[i][j] >> w[i][j];
}
for (int i = 1; i <= n; i++)
for (int j = m; j >= 0; j--)//从前往后枚举每一组物品,从大到小枚举所有体积
for (int k = 0; k < s[i]; k++)//枚举所有选择
if (v[i][k] <= j)//如果第i组,第k件物品<=j的话,我们才能往下进行,即要注意体积大小
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
cout << f[m] << endl;
return 0;
}