目录
一:思路简介
二:0-1 背包
三:完全背包
四:多重背包
五:分组背包
一:思路简介

n 个物品,容量为V的背包
Vi 体积 Wi 价值(权重)
二:0-1 背包
每件物品最多只能用1次(要么0次,要么1次)
集合划分:f(i,j)=Max(f(i-1,j),f(i-1,j-Vi)+Wi)


0次(不含i):一定存在
1次(含i):仅当v<=j才可以
暴力
#include <iostream>
using namespace std;
const int N = 1010;
int n, v;
int v[N], w[N];
int f[N][N];
int main() {
scanf("%d%d", &n, &v);
for(int i = 1; i <= n; i++) scanf("%d%d", &v[i], &w[i]);
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= v; j++) {
f[i][j] = f[i - 1][j];//默认不含i:0次
if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);//当vi<=j,选最大的
}
}
printf("%d", f[n][v]);
}
降维优化
(原先用二维数组表示状态,可以换成一维数组,用滚动数组(下一层只用到上一层来算,滚动交替计算)的方式。注:动态规划的优化,通常都是对代码或者状态转移方程,做等价变型)
- f(i,) 只用到了f(i-1,)所以提示可以用滚动数组;
- 两个函数第二个元素都<=j,所以可以改成一维数组;
- 把i直接删掉;
- j=0--vi无意义,所以删掉判断条件,j从vi开始;
- 内循环从小到大计算的将是max(f[i,j],f[i,j-v[i]]+w[i]),所以改成从大到小循环时f( ,j-v[i])还没有被更新,就会是f( i-1,j-v[i]+w[i]);
for(int i = 1; i <= n; i++) {
for(int j =m; j >= v[i]; j--) {
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
三:完全背包
每件物品都有无限次


暴力
#include <iostream>
using namespace std;
const int MAX = 1010;
int N, V;
int f[MAX][MAX];
int v[MAX], w[MAX];
int main() {
scanf("%d%d", &N, &V);
for(int i = 1; i <= N; i++) scanf("%d%d", &v[i], &w[i]);
for(int i = 1; i <= N; i++) {
for(int j = 0; j <= V; j++) {
for(int k = 0; k * v[i]<=j; k++)
f[i][j] =max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
}
}
printf("%d", f[N][V]);
}
优化类似01

根据上图的推导过程,我们实际上可以用2个状态来推导出 f ( i , j ) ,即 f ( i , j ) = m a x { f ( i − 1 , j ) , f ( i , j − v ) + w },此时f ( i , j )的推导就和 k 无关了。于是根据这个状态转移方程,我们写成代码如下
for(int i = 1; i <= N; i++) {
for(int j = 0; j <= V; j++) {
f[i][j] = f[i - 1][j];
if(j >= v[i]) f[i][j] =max(f[i][j], f[i][j - v[i]] + w[i]);
}
}
降维优化
注意:此处降维优化与01背包的区别是内循环不用从大到小,因为上述第一次优化后f[i][j] =max(f[i][j], f[i][j - v[i]] + w[i]) 不是f(i-1, ),所以不用改循环。
for(int i = 1; i <= N; i++) {
for(int j =v[i]; j <= V; j++) {
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
}
四:多重背包
每个物品最多有Si个
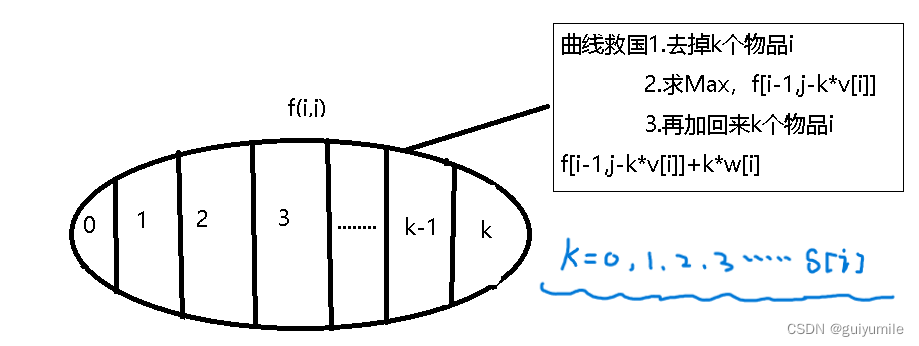
多重背包的状态转移方程,和完全背包一致,如下
f ( i , j ) = m a x { f ( i − 1 , j − v [ i ] × k ) + k × v [ i ] } ,k ∈ [ 0 , s [ i ] ]
多重背包只是对每个物品,多了数量限制,而完全背包没有数量限制。

暴力
#include <iostream>
using namespace std;
const int MAX = 1010;
int N, V;
int f[MAX][MAX];
int v[MAX], w[MAX], s[MAX];
int main() {
scanf("%d%d", &N, &V);
for(int i = 1; i <= N; i++) scanf("%d%d%d", &v[i], &w[i], &s[i]);
for(int i = 1; i <= N; i++) {
for(int j = 0; j <= V; j++) {
for(int k = 0;k <= s[i] && k*v[i]<=j; k++)
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
}
}
printf("%d", f[N][V]);
}
优化方法一:采用完全背包的优化方法时:只有中间一部分是相同的,无法进行替换(X)
优化方法二:二进制,以s[i]=200为例:
首先1,2,4,8,16,32,64能够凑出到(64*2)-1=127,这是毋庸置疑的。而0到127种的任意一种组合,再额外加一个73,就能凑出73到200,所以上面的8个数就能凑出0到200中的任意一个数。
所以,对于物品i,共有s[i]个,其实我们可以把s[i]个物品,拆分成 log s[i],然后对这些新的物品,做一次01背包问题即可。
#include <iostream>
// 因为物品共有N=1000个,而每个物品的s[i]最大到2000,所以每个物品能拆成log(2000)≈11, 实际计算出来是小于11的,
// 所以拆分后的物品总数不超过 1000 * 11 = 11000, 所以我们的N开到11000即可
// 由于数组下标从1开始, 所以我们至少要开到11001
const int N = 11001;
int n, m;
int v[N], w[N], f[N];
int main() {
scanf("%d%d", &n, &m);
int cnt = 0;
for(int i = 1; i <= n; i++) {
// 处理输入, 将 s[i] 个物品拆分成 log(s[i]) 个
int a, b, s;
scanf("%d%d%d", &a, &b, &s);
int k = 1;
while(k <= s) {
cnt++;
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k *= 2;
}
if(s > 0) {
cnt++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
n = cnt; // 总共拆分成了多少个新的物品
// 对新的物品, 做一次01背包问题, 这里直接写了一维数组优化后的01背包
for(int i = 1; i <= n; i++) {
for(int j = m; j >= v[i]; j--) {
f[j] = std::max(f[j], f[j - v[i]] + w[i]);
}
}
printf("%d", f[m]);
}
五:分组背包
n组,每组只能选1个
01背包的状态转移,是枚举第i个物品选或者不选;
完全背包和多重背包,是枚举第i个物品,选0,1,2,3,4,.... 个
而分组背包,枚举的是第i个分组,选哪一个,或者不选
分组背包的状态转移方程为:
f ( i , j ) = m a x { f ( i − 1 , j ) , f ( i − 1 , j − v [ i , k ] ) + w [ i , k ]},k ∈ [ 1 , s [ i ] ]
其中 v [ i , k ]表示第 i 组中的第 k个物品的体积,w [ i , k ]同理
#include <iostream>
using namespace std;
const int N = 110;
int n, m;
int v[N][N], w[N][N], s[N];
int f[N];
int main() {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) {
scanf("%d", &s[i]);
for(int j = 0; j < s[i]; j++) {
scanf("%d%d", &v[i][j], &w[i][j]);
}
}
for(int i = 1; i <= n; i++) {
for(int j = m; j >= 0; j--) {
for(int k = 0; k < s[i]; k++) {
if(v[i][k] <= j) {
f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
}
}
}
}
printf("%d", f[m]);
}