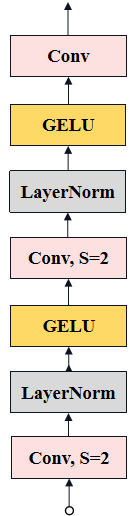
来自0x3f
【从周赛中学算法 - 2022 年周赛题目总结(下篇)】:https://leetcode.cn/circle/discuss/WR1MJP/
【【灵茶山艾府】2022 年周赛题目总结(上篇)】https://leetcode.cn/circle/discuss/G0n5iY/
学习动态规划是否有捷径?我的看法是没有捷径,多做题就是最好的训练方法。对于不会做的题目,要反复训练到一分钟内能想出状态转移方程为止。
如果你很难想出状态转移方程,以及递推的顺序,可以先从记忆化搜索开始思考,然后转换到递推上。
记忆化搜索像是自动挡,无需思考递推顺序,边界条件也容易确认;而递推像是手动挡,需要仔细确认递推的顺序以及初始值。但记忆化搜索并不是万能的,某些题目递推的写法可以结合数据结构等来优化时间复杂度。
注:常见于周赛第四题(约占 28%),偶见于第三题(约占 9%)
灵神 - 2022下半年周赛题目总结(动态规划)
| 题目 | 难度 | 备注 |
|---|---|---|
| 2466. 统计构造好字符串的方案数 | 1694 | 本质上是 70. 爬楼梯 |
| 2400. 恰好移动 k 步到达某一位置的方法数目 | 1751 | 也有数学解 |
| 2369. 检查数组是否存在有效划分 | 1780 | |
| 2370. 最长理想子序列 | 1835 | |
| 2327. 知道秘密的人数 | 1894 | |
| 2435. 矩阵中和能被 K 整除的路径 | 1952 | |
| 2328. 网格图中递增路径的数目 | 2001 | |
| 2472. 不重叠回文子字符串的最大数目 | 2013 | 中心扩展法 |
| 2430. 对字母串可执行的最大删除数 | 2102 | |
| 2376. 统计特殊整数 | 2120 | 数位 DP,这类题目非常套路,掌握模板后就可以随便秒了 |
| 2407. 最长递增子序列 II | 2280 | 线段树优化 DP |
| 2458. 移除子树后的二叉树高度 | 2299 | 树形 DP |
| 2478. 完美分割的方案数 | 2344 | |
| 2518. 好分区的数目 | 2414 | 01 背包,需要一些思维转换 |
| 2463. 最小移动总距离 | 2454 |
灵神 - 2022上半年周赛题目总结(动态规划)
| 题目 | 难度 | 备注 |
|---|---|---|
| 2140. 解决智力问题 | 1709 | 线性 DP |
| 2167. 移除所有载有违禁货物车厢所需的最少时间 | 2219 | 线性 DP |
| 2172. 数组的最大与和 | 2392 | 状压 DP |
| 2188. 完成比赛的最少时间 | 2315 | 线性 DP |
| 2209. 用地毯覆盖后的最少白色砖块 | 2105 | 线性 DP |
| 2218. 从栈中取出 K 个硬币的最大面值和 | 2157 | 分组背包 |
| 2246. 相邻字符不同的最长路径 | 2126 | 树形 DP |
| 2262. 字符串的总引力 | 2033 | 线性 DP |
| 2266. 统计打字方案数 | 1856 | 线性 DP |
| 2272. 最大波动的子字符串 | 2515 | 线性 DP |
| 2305. 公平分发饼干 | 1886 | 子集状压 DP |
| 2312. 卖木头块 | 2363 | 线性 DP |
| 2318. 不同骰子序列的数目 | 2090 | 线性 DP |
| 2320. 统计放置房子的方式数 | 1607 | 线性 DP |
| 2321. 拼接数组的最大分数 | 1790 | 线性 DP |
| LCP 53. 守护太空城 | - | 子集状压 DP |
灵神-从周赛中学算法(动态规划😰)
2466. 统计构造好字符串的方案数
难度中等15
给你整数 zero ,one ,low 和 high ,我们从空字符串开始构造一个字符串,每一步执行下面操作中的一种:
- 将
'0'在字符串末尾添加zero次。 - 将
'1'在字符串末尾添加one次。
以上操作可以执行任意次。
如果通过以上过程得到一个 长度 在 low 和 high 之间(包含上下边界)的字符串,那么这个字符串我们称为 好 字符串。
请你返回满足以上要求的 不同 好字符串数目。由于答案可能很大,请将结果对 109 + 7 取余 后返回。
示例 1:
输入:low = 3, high = 3, zero = 1, one = 1
输出:8
解释:
一个可能的好字符串是 "011" 。
可以这样构造得到:"" -> "0" -> "01" -> "011" 。
从 "000" 到 "111" 之间所有的二进制字符串都是好字符串。
示例 2:
输入:low = 2, high = 3, zero = 1, one = 2
输出:5
解释:好字符串为 "00" ,"11" ,"000" ,"110" 和 "011" 。
提示:
1 <= low <= high <= 1051 <= zero, one <= low
记忆化搜索:
class Solution {
private static final int MOD = (int)1e9 + 7;
int zero, one, low, high;
int len = 0;
int[] cache;
public int countGoodStrings(int low, int high, int zero, int one) {
this.low = low;
this.high = high;
this.zero = zero;
this.one = one;
cache = new int[high + 1];
Arrays.fill(cache, -1);
return dfs(0);
}
// 定义dfs(i) 为长度为 high - i 时的好字符串数目
public int dfs(int len){
if(len > high) return 0;
if(cache[len] >= 0) return cache[len];
int res = 0;
if(len >= low && len <= high) res++;
res += dfs(len + zero) % MOD;
res += dfs(len + one) % MOD;
return cache[len] = res % MOD;
}
}
转成递推:(转不来😭,而且不会将dfs(0)的调用过程变为dfs(high))
定义 f[i] 表示构造长为 i 的字符串的方案数
初始值:f[0] = 1:构造空串的方案数为 1
状态转移方程:f[i] = (f[i] + f[i-one] + f[i-zero])
class Solution {
private static final int MOD = (int)1e9 + 7;
public int countGoodStrings(int low, int high, int zero, int one) {
// f[i] 长度为i的字符串有几种组合 可以从zero来 也可以one来
int[] f = new int[high+1]; //状态定义:f[i] 表示构造长为 i 的字符串的方案数
f[0] = 1; // 初始值:构造空串的方案数为 1
int ans = 0;
for(int i = 1; i <= high; i++){
if(i >= one) f[i] = (f[i] + f[i-one]) % MOD;
if(i >= zero) f[i] = (f[i] + f[i-zero]) % MOD;
if(i >= low) ans = (ans + f[i]) % MOD;
}
return ans % MOD;
}
}
2400. 恰好移动 k 步到达某一位置的方法数目
难度中等41
给你两个 正 整数 startPos 和 endPos 。最初,你站在 无限 数轴上位置 startPos 处。在一步移动中,你可以向左或者向右移动一个位置。
给你一个正整数 k ,返回从 startPos 出发、恰好 移动 k 步并到达 endPos 的 不同 方法数目。由于答案可能会很大,返回对 109 + 7 取余 的结果。
如果所执行移动的顺序不完全相同,则认为两种方法不同。
注意:数轴包含负整数。
示例 1:
输入:startPos = 1, endPos = 2, k = 3
输出:3
解释:存在 3 种从 1 到 2 且恰好移动 3 步的方法:
- 1 -> 2 -> 3 -> 2.
- 1 -> 2 -> 1 -> 2.
- 1 -> 0 -> 1 -> 2.
可以证明不存在其他方法,所以返回 3 。
示例 2:
输入:startPos = 2, endPos = 5, k = 10
输出:0
解释:不存在从 2 到 5 且恰好移动 10 步的方法。
提示:
1 <= startPos, endPos, k <= 1000
记忆化搜索
class Solution {
private static final int MOD = (int)1e9+7;
int k, endPos;
Map<String, Integer> map;
public int numberOfWays(int startPos, int endPos, int k) {
this.k = k;
this.endPos = endPos;
map = new HashMap<>();
return dfs(startPos, 0);
}
// 定义dfs(pos, idx) 为当前在pos位置,已经走了idx步,还剩endPos-idx走到终点的方法数
public int dfs(int pos, int idx){
if(idx == k){
if(pos == endPos) return 1;
else return 0;
}
// 优化:如果在递归过程中剩余步数走不到终点endPos位置,则直接返回0
if(Math.abs(pos - endPos) > (k - idx)) return 0;
String key = pos + "_" + idx;
if(map.containsKey(key)) return map.get(key);
int res = 0;
res += dfs(pos + 1, idx+1) % MOD;
res += dfs(pos - 1, idx+1) % MOD;
map.put(key, res % MOD);
return res % MOD;
}
}
背包问题的解法:
// https://leetcode.cn/problems/number-of-ways-to-reach-a-position-after-exactly-k-steps/solution/by-endlesscheng-6yvy/
/**
假定 end 在 start 的右边,那么一定有 | end - start | 步是朝右边移动的
如果要满足要求,剩下的(k - | end - start | ) 步,肯定一半是朝左、一半是朝右。
即在 [ 1 .. k ] 步中,有(k - | end - start | ) / 2 步是朝左的,
当我们确定这 (k - | end - start | ) / 2 步是哪几步时,整个移动路径是可以确定的,
所以原问题就等价于:在 k 件物品中,挑选物品,每件物品占用容量为1,
求恰好放进容量为 (k - | end - start | ) / 2 的背包里的方案数。
*/
class Solution {
private static final int MOD = (int)1e9+7;
public int numberOfWays(int startPos, int endPos, int k) {
int dist = endPos - startPos;
if(k < Math.abs(dist) || ((k - dist) & 1) == 1)
return 0;
int cap = (k - Math.abs(dist)) / 2;
long[] dp = new long[cap + 1];
dp[0] = 1;
for(int i = 1; i <= k; i++){
for(int j = cap; j >= 0; j--){
if(j >= 1){
dp[j] = (dp[j] + dp[j-1]) % MOD;
}
}
}
return (int)dp[cap];
}
}
2369. 检查数组是否存在有效划分
难度中等33
给你一个下标从 0 开始的整数数组 nums ,你必须将数组划分为一个或多个 连续 子数组。
如果获得的这些子数组中每个都能满足下述条件 之一 ,则可以称其为数组的一种 有效 划分:
- 子数组 恰 由
2个相等元素组成,例如,子数组[2,2]。 - 子数组 恰 由
3个相等元素组成,例如,子数组[4,4,4]。 - 子数组 恰 由
3个连续递增元素组成,并且相邻元素之间的差值为1。例如,子数组[3,4,5],但是子数组[1,3,5]不符合要求。
如果数组 至少 存在一种有效划分,返回 true ,否则,返回 false 。
示例 1:
输入:nums = [4,4,4,5,6]
输出:true
解释:数组可以划分成子数组 [4,4] 和 [4,5,6] 。
这是一种有效划分,所以返回 true 。
示例 2:
输入:nums = [1,1,1,2]
输出:false
解释:该数组不存在有效划分。
提示:
2 <= nums.length <= 1051 <= nums[i] <= 106
题解:划分型DP( 划分 -> 子问题 -> DP,拿两个数出来划分,剩下部分即变成了更小的子问题)
class Solution {
/**
DP五部曲:
1.状态定义:f[i+1]代表考虑将[0,i]是否能被有效划分,有则为true,没有则为false
2.状态转移:f[i+1]的转移有3种可能:
2.1 由f[i-1]转移过来,且nums[i-1]==nums[i]
2.2 由f[i-2]转移过来,且nums[i-2]==nums[i-1]==nums[i]
2.3 由f[i-2]转移过来,且nums[i-1]==nums[i-2]+1;nums[i]==nums[i-1]+1
其中一种能转移过来即可
3.初始化:f[0]=true
4.遍历顺序:正序遍历
5.返回形式:返回f[n]
*/
public boolean validPartition(int[] nums) {
int n = nums.length;
// 状态定义:f[i+1] 表示从 nums[0] 到 nums[i] 的这些元素能否有效划分
boolean[] f = new boolean[n+1];
f[0] = true; // 初始值, 答案 f[n]
for(int i = 1; i < n; i++){
if(f[i-1] && nums[i] == nums[i-1])
f[i+1] = true;
if(i > 1 && f[i-2] && (nums[i] == nums[i-1] && nums[i-1] == nums[i-2]))
f[i+1] = true;
if(i > 1 && f[i-2] && (nums[i] == nums[i-1]+1 && nums[i-1] == nums[i-2]+1))
f[i+1] = true;
}
return f[n];
}
}
2370. 最长理想子序列
难度中等35
给你一个由小写字母组成的字符串 s ,和一个整数 k 。如果满足下述条件,则可以将字符串 t 视作是 理想字符串 :
t是字符串s的一个子序列。t中每两个 相邻 字母在字母表中位次的绝对差值小于或等于k。
返回 最长 理想字符串的长度。
字符串的子序列同样是一个字符串,并且子序列还满足:可以经由其他字符串删除某些字符(也可以不删除)但不改变剩余字符的顺序得到。
**注意:**字母表顺序不会循环。例如,'a' 和 'z' 在字母表中位次的绝对差值是 25 ,而不是 1 。
示例 1:
输入:s = "acfgbd", k = 2
输出:4
解释:最长理想字符串是 "acbd" 。该字符串长度为 4 ,所以返回 4 。
注意 "acfgbd" 不是理想字符串,因为 'c' 和 'f' 的字母表位次差值为 3 。
示例 2:
输入:s = "abcd", k = 3
输出:4
解释:最长理想字符串是 "abcd" ,该字符串长度为 4 ,所以返回 4 。
提示:
1 <= s.length <= 1050 <= k <= 25s由小写英文字母组成
(超时)方法一:转化为经典问题:LIS最长递增子序列问题
- 看到数据范围
10^5就应该想到这个办法行不通
class Solution {
public int longestIdealString(String s, int k) {
int n = s.length();
int[] f = new int[n+1]; // 定义f[i]表示以i结尾的字符串 最长理想子序列的长度
int res = 0;
Arrays.fill(f, 1);
for(int i = 1; i < n; i++){
for(int j = i-1; j >= 0; j--){
if(Math.abs((s.charAt(i) - 'a') - (s.charAt(j) - 'a')) <= k){
f[i] = Math.max(f[i], f[j]+1);
}
}
res = Math.max(res, f[i]);
}
return res;
}
}
在LIS问题上进一步进行考虑: 存上一个字母出现的位置
题解:https://leetcode.cn/problems/longest-ideal-subsequence/solution/by-endlesscheng-t7zf/
字符串题目套路: 枚举字符。
定义 f[i][c] 表示 s 的前i个字母中的以 c 结尾的理想字符串的最长长度
选s[i]作为理想字符串中的字符,需要从f[i-1]中的[s[i]-k, s[i]+k]范围内的字符转移过来
不选s[i],则f[i][c] = f[i-1][c]
class Solution {
public int longestIdealString(String s, int k) {
int n = s.length();
// f[i][j] 表示从 s 的前 i 个字符中选一个末尾字符为 c 的理想字符串的最长长度
int[][] f = new int[n+1][26];
for(int i = 1; i <= n; i++){
int c = s.charAt(i-1) - 'a';
// 不选c:f[i]直接从状态f[i-1]转移得到
for(int j = 0; j < 26; j++){
f[i][j] = f[i-1][j];
}
//选s[i]作为理想字符串中的字符,需要从f[i-1]中的[s[i]-k, s[i]+k]范围内的字符转移过来
for(int j = Math.max(c-k, 0); j <= Math.min(c+k, 25); j++){
f[i][c] = Math.max(f[i][c], f[i-1][j]+1);
}
}
// 最终答案为max(f[n][0~25])
int res = 0;
for(int i = 0; i < 26; i++) res = Math.max(res, f[n][i]);
return res;
}
}
空间优化
class Solution {
// 空间优化:将第一维度优化掉,因为只从上一个状态f[i-1]进行转移,因此可以优化掉
public int longestIdealString(String s, int k) {
int n = s.length();
int[] f = new int[26];
for(int i = 0; i < n; i++){
int c = s.charAt(i) - 'a';
// 不选c,直接继承上一层的状态f[i-1],优化掉第一维度后,就直接继承了,不用代码实现
// 选c,f[i][c]=max(f[i-1][c-k~c+k])+1
for(int j = Math.max(c-k, 0); j <= Math.min(c+k, 25); j++){
f[c] = Math.max(f[c], f[j]);
}
f[c]++;
}
// 最终答案为max(f[0~25])
int res = 0;
for(int i = 0; i < 26; i++) res = Math.max(res, f[i]);
return res;
}
}
🎉2327. 知道秘密的人数(斐波那契兔子问题变形)
难度中等68
在第 1 天,有一个人发现了一个秘密。
给你一个整数 delay ,表示每个人会在发现秘密后的 delay 天之后,每天 给一个新的人 分享 秘密。同时给你一个整数 forget ,表示每个人在发现秘密 forget 天之后会 忘记 这个秘密。一个人 不能 在忘记秘密那一天及之后的日子里分享秘密。
给你一个整数 n ,请你返回在第 n 天结束时,知道秘密的人数。由于答案可能会很大,请你将结果对 109 + 7 取余 后返回。
示例 1:
输入:n = 6, delay = 2, forget = 4
输出:5
解释:
第 1 天:假设第一个人叫 A 。(一个人知道秘密)
第 2 天:A 是唯一一个知道秘密的人。(一个人知道秘密)
第 3 天:A 把秘密分享给 B 。(两个人知道秘密)
第 4 天:A 把秘密分享给一个新的人 C 。(三个人知道秘密)
第 5 天:A 忘记了秘密,B 把秘密分享给一个新的人 D 。(三个人知道秘密)
第 6 天:B 把秘密分享给 E,C 把秘密分享给 F 。(五个人知道秘密)
示例 2:
输入:n = 4, delay = 1, forget = 3
输出:6
解释:
第 1 天:第一个知道秘密的人为 A 。(一个人知道秘密)
第 2 天:A 把秘密分享给 B 。(两个人知道秘密)
第 3 天:A 和 B 把秘密分享给 2 个新的人 C 和 D 。(四个人知道秘密)
第 4 天:A 忘记了秘密,B、C、D 分别分享给 3 个新的人。(六个人知道秘密)
提示:
2 <= n <= 10001 <= delay < forget <= n
这个题就是斐波那契兔子问题的变形,Mortal Fibonacci Rabbits
大意就是:新出生的兔子需要delay天成熟,然后成熟之后(包括当天)每天开始生新兔子,直到forget-1天后死亡,求问最后一天还存活多少个兔子?
方法一:定义dp[i]表示第 i 天所有知道秘密的人数
那么第 i - forget 天就是第i天忘记的人数, i - delay 就是第i天可以分享的人数
那么第i天可以分享秘密的人数 = 可分享人数 - 今天忘记人数。第i天 = 第i - 1天的总人数 + 分享人数。
- 注意:第
i天还包括前面忘记的人数,我们只是让他们不再分享。
所以最后答案还需减去总共忘记的人数,即dp[n - forget]。复杂度O(n)
class Solution {
private static final int MOD = (int)1e9 + 7;
public int peopleAwareOfSecret(int n, int delay, int forget) {
long[] dp = new long[n+1];
dp[1] = 1;// 在第 1 天,有一个人发现了一个秘密。
for(int i = 2; i <= n; i++){
long shared = i >= delay ? dp[i-delay] : 0; // 可以分享秘密的人数
long forgt = i >= forget ? dp[i-forget] : 0; // 在第i天忘记秘密的人数
// 第i天可以分享秘密的人数 = 可分享人数 - 今天忘记人数
dp[i] = (dp[i-1] + shared - forgt + MOD) % MOD;
System.out.println(dp[i]);
}
// 第i天还包括前面忘记的人数, 所以最后答案还需减去总共忘记的人数
return (int)(dp[n] - dp[n-forget] + MOD) % MOD;
}
}
打印结果:
// output : (1) 1 2 3 4 6
样例:
输入:n = 6, delay = 2, forget = 4
输出:5
解释:
第 1 天:假设第一个人叫 A 。(一个人知道秘密)
第 2 天:A 是唯一一个知道秘密的人。(一个人知道秘密)
第 3 天:A 把秘密分享给 B 。(两个人知道秘密)
第 4 天:A 把秘密分享给一个新的人 C 。(三个人知道秘密)
第 5 天:A 忘记了秘密,B 把秘密分享给一个新的人 D 。(三个人知道秘密)
第 6 天:B 把秘密分享给 E,C 把秘密分享给 F 。(五个人知道秘密)
方法二:只需要统计第i天新增的人数就好了
- 每一个第
i天知道秘密的人,都对[i+delay,i+forget)这个区间有贡献,从前往后推即可
class Solution {
private static final int MOD = (int)1e9 + 7;
public int peopleAwareOfSecret(int n, int delay, int forget) {
// 只需要统计第i天新增的人数就好了
// 每一个第i天知道秘密的人,都对[i+delay,i+forget)这个区间有贡献,从前往后推即可
int[] dp = new int[n];
dp[0] = 1;
for(int i = 0; i < n; i++){
for(int j = i + delay; j < Math.min(n, i + forget); j++){
dp[j] = (dp[j] + dp[i]) % MOD;
}
}
// 知道秘密的总人数其实就等于从最后一天往前推forget天的人数和。
int sum = 0;
for(int i = n - forget; i < n; i++){
sum = (sum + dp[i]) % MOD;
}
return sum;
}
}
2435. 矩阵中和能被 K 整除的路径
难度困难31
给你一个下标从 0 开始的 m x n 整数矩阵 grid 和一个整数 k 。你从起点 (0, 0) 出发,每一步只能往 下 或者往 右 ,你想要到达终点 (m - 1, n - 1) 。
请你返回路径和能被 k 整除的路径数目,由于答案可能很大,返回答案对 109 + 7 取余 的结果。
示例 1:
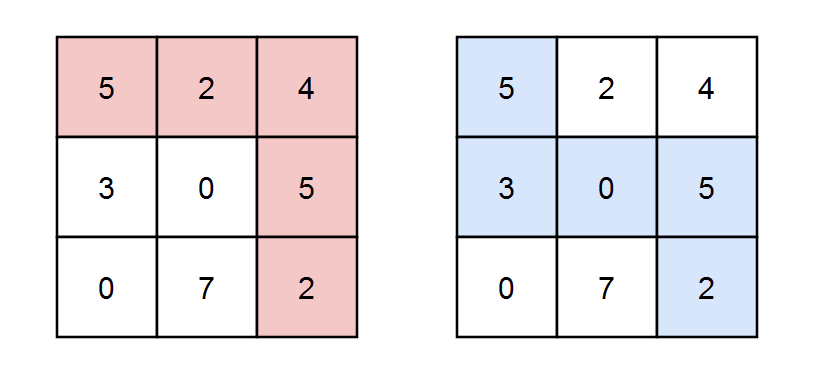
输入:grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3
输出:2
解释:有两条路径满足路径上元素的和能被 k 整除。
第一条路径为上图中用红色标注的路径,和为 5 + 2 + 4 + 5 + 2 = 18 ,能被 3 整除。
第二条路径为上图中用蓝色标注的路径,和为 5 + 3 + 0 + 5 + 2 = 15 ,能被 3 整除。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 5 * 1041 <= m * n <= 5 * 1040 <= grid[i][j] <= 1001 <= k <= 50
自己写的第一版:记忆化搜索,超时,记忆化搜索不是万能的,合理的记忆化搜索是好的递归方法
这个对sum的维度可以写为k,因为最后求的是能被k整除的路径个数,取余节省递归次数
例如:
- 到
(x,y)点时,假设这条路径总和为sum,最后结果和sum%k是相同的,因为10%3 = 1%3
class Solution {
private static final int MOD = (int)1e9 + 7;
int[][] grid;
Map<String, Integer> map = new HashMap<>();
int k = 0;
public int numberOfPaths(int[][] grid, int k) {
this.grid = grid;
this.k = k;
int n = grid.length, m = grid[0].length;
return dfs(n-1, m-1, grid[n-1][m-1]);
}
// 定义dfs(i, j, sum) 表示从(n,m)到(i,j)的和为sum,能被k整除的路径个数
public int dfs(int i, int j, int sum){
if(i < 0 || j < 0) return 0;
if(i == 0 && j == 0){
return sum % k == 0 ? 1 : 0;
}
String key = i + ":" + j + ":" + sum;
if(map.containsKey(key)) return map.get(key);
int res = 0;
if(i > 0) res = (res + dfs(i-1, j, sum + grid[i-1][j])) % MOD;
if(j > 0) res = (res + dfs(i, j-1, sum + grid[i][j-1])) % MOD;
map.put(key, res);
return res;
}
}
修改后:记忆化搜索
class Solution {
private static final int MOD = (int)1e9 + 7;
int[][] grid;
int[][][] cache;
int k = 0;
public int numberOfPaths(int[][] grid, int k) {
this.grid = grid;
this.k = k;
int n = grid.length, m = grid[0].length;
cache = new int[n][m][k];
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
Arrays.fill(cache[i][j], -1);
return dfs(n-1, m-1, grid[n-1][m-1] % k);
}
// 定义dfs(i, j, sum) 表示从(n,m)到(i,j)的和为sum,能被k整除的路径个数
public int dfs(int i, int j, int sum){
if(i < 0 || j < 0) return 0;
if(i == 0 && j == 0){
return sum % k == 0 ? 1 : 0;
}
if(cache[i][j][sum] >= 0) return cache[i][j][sum];
int res = 0;
if(i > 0) res = (res + dfs(i-1, j, (sum + grid[i-1][j]) % k)) % MOD;
if(j > 0) res = (res + dfs(i, j-1, (sum + grid[i][j-1]) % k)) % MOD;
return cache[i][j][sum] = res;
}
}
递归转成递推:
class Solution {
private static final int MOD = (int)1e9 + 7;
public int numberOfPaths(int[][] grid, int k) {
int n = grid.length, m = grid[0].length;
// 定义f[i, j, k] 表示从(0,0)到(i,j)的和为sum%k的路径个数
int[][][] f = new int[n+1][m+1][k];
// 表示当i==0&&j==0时,和为0(取余k=0)的路径个数为1
f[0][1][0] = 1; // 行列都需要一个维度表示初始化值,f[0][1][0]和f[0][0][1]只要有一个为1就行,最后返回f[n][m][0];
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
for(int v = 0; v < k; v++){
f[i+1][j+1][(v + grid[i][j]) % k] = (f[i+1][j][v] + f[i][j+1][v]) % MOD;
}
}
}
return f[n][m][0];
}
}
2328. 网格图中递增路径的数目
难度困难30收藏分享切换为英文接收动态反馈
给你一个 m x n 的整数网格图 grid ,你可以从一个格子移动到 4 个方向相邻的任意一个格子。
请你返回在网格图中从 任意 格子出发,达到 任意 格子,且路径中的数字是 严格递增 的路径数目。由于答案可能会很大,请将结果对 109 + 7 取余 后返回。
如果两条路径中访问过的格子不是完全相同的,那么它们视为两条不同的路径。
示例 1:
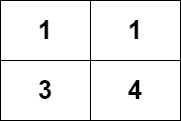
输入:grid = [[1,1],[3,4]]
输出:8
解释:严格递增路径包括:
- 长度为 1 的路径:[1],[1],[3],[4] 。
- 长度为 2 的路径:[1 -> 3],[1 -> 4],[3 -> 4] 。
- 长度为 3 的路径:[1 -> 3 -> 4] 。
路径数目为 4 + 3 + 1 = 8 。
示例 2:
输入:grid = [[1],[2]]
输出:3
解释:严格递增路径包括:
- 长度为 1 的路径:[1],[2] 。
- 长度为 2 的路径:[1 -> 2] 。
路径数目为 2 + 1 = 3 。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10001 <= m * n <= 1051 <= grid[i][j] <= 105
题解:https://leetcode.cn/problems/number-of-increasing-paths-in-a-grid/solution/ji-yi-hua-sou-suo-pythonjavacgo-by-endle-xecc/
这种依赖暂未计算的状态的情况,还是记忆化搜索好(只要递归有终止状态,总会有一个格子无法往下走)。
class Solution {
/**
为什么是动态规划?
把从格子 (i,j) 出发可以得到的路径数,当作一个子问题 dp[i][j]
1.到达同一个格子,有多种不同的方式 ->有很多重复的子问题
2.计算 dp[i][j],与怎么到达 (i,j) 无关 -> 无后效性
3. 从格子 (i,j) 出发的方案数,恰好等于:
(i,j) 相邻格子且其值比 (i,j) 大的这些格子的方案数之和,加上 格子(i,j)本身组成的路径 -> 最优子结构
*/
private static final int MOD = (int) 1e9 + 7;
private static final int[][] dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
int m, n;
int[][] grid, cache;
public int countPaths(int[][] grid) {
m = grid.length;
n = grid[0].length;
this.grid = grid;
cache = new int[m][n];
for(int i = 0; i < m; i++) Arrays.fill(cache[i], -1);
int res = 0;
for(int i = 0; i < m; i++)
for(int j = 0; j < n; j++)
res = (res + dfs(i, j)) % MOD;
return res;
}
public int dfs(int i, int j){
if(cache[i][j] != -1) return cache[i][j];
int res = 1;
for(int[] d : dirs){
int x = i + d[0], y = j + d[1];
if(0 <= x && x < m && 0 <= y && y < n &&
grid[x][y] > grid[i][j])
res = (res + dfs(x, y)) % MOD;
}
return cache[i][j] = res;
}
}
🎉2472. 不重叠回文子字符串的最大数目
难度困难33
给你一个字符串 s 和一个 正 整数 k 。
从字符串 s 中选出一组满足下述条件且 不重叠 的子字符串:
- 每个子字符串的长度 至少 为
k。 - 每个子字符串是一个 回文串 。
返回最优方案中能选择的子字符串的 最大 数目。
子字符串 是字符串中一个连续的字符序列。
示例 1 :
输入:s = "abaccdbbd", k = 3
输出:2
解释:可以选择 s = "abaccdbbd" 中斜体加粗的子字符串。"aba" 和 "dbbd" 都是回文,且长度至少为 k = 3 。
可以证明,无法选出两个以上的有效子字符串。
示例 2 :
输入:s = "adbcda", k = 2
输出:0
解释:字符串中不存在长度至少为 2 的回文子字符串。
提示:
1 <= k <= s.length <= 2000s仅由小写英文字母组成
class Solution {
/**
DP 子问题?
-原问题是什么:s不重叠回文子字符串的最大数目
- 更小的子问题是什么?
考虑最后一个字符如何操作?
不选:s-1不重叠回文子字符串的最大数目
选:满足字串长度至少为k,字串是回文的,且len(s)-k前又是一个更小的子问题
f[0] 表示空串
f[i] 表示s[0..i-1] i-1不重叠回文子字符串的最大数目
*/
public int maxPalindromes(String s, int k) {
int n = s.length();
// 定义f[i]表示s[0..i-1]中不重叠的回文子字符串的最大数目
int[] f = new int[n + 1];
f[0] = 0; // 初始化:定义f[0]=0,表示空字符串,最后返回f[n]
// 中心扩展法找最长回文串
// 回文串分为奇回文(n种中心位置)和偶回文(n-1种中心位置)两种,如何进行处理?
// 枚举这2n-1种中心位置,用0表示奇回文的情况,1表示偶回文的情况,2表示奇回文的情况....
for (int i = 0; i < 2 * n - 1; i++) {
// 更加优雅的方式枚举所有奇数和偶数的中心点位置(利用奇偶性来表示是奇回文情况还是偶回文情况)
int l = i / 2, r = l + i % 2;
// 不选s[l] : f[l+1] = f[l]
f[l+1] = Math.max(f[l+1], f[l]);
// 选s[l] : 向两侧扩展
while(l >= 0 && r < n && s.charAt(l) == s.charAt(r)){ // 可以扩展,s[l..r]是回文串
if(r - l + 1 >= k){// 贪心处理,f[l]是非递减的,更小的f[l]也不会影响答案
// 找到了满足条件的回文串 : s[r]包含在回文串中,并且回文长度大于等于k
f[r+1] = Math.max(f[r+1], f[l] + 1);
break;
}
l--; r++;
}
}
return f[n];
}
}
647. 回文子串【回文字串数目/最长回文子串】
难度中等1141收藏分享切换为英文接收动态反馈
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:s = "abc"
输出:3
解释:三个回文子串: "a", "b", "c"
示例 2:
输入:s = "aaa"
输出:6
解释:6个回文子串: "a", "a", "a", "aa", "aa", "aaa"
提示:
1 <= s.length <= 1000s由小写英文字母组成
题解:https://leetcode.cn/problems/palindromic-substrings/solution/liang-dao-hui-wen-zi-chuan-de-jie-fa-xiang-jie-zho/
方法一:动态规划
首先这一题可以使用动态规划来进行解决:
- 状态:
dp[i][j]表示字符串s在[i,j]区间的子串是否是一个回文串。 - 状态转移方程:
当 s[i] == s[j] && (j - i < 2 || dp[i + 1][j - 1])时,dp[i][j]=true,否则为false
这个状态转移方程是什么意思呢?
- 当只有一个字符时,比如
a自然是一个回文串。 - 当有两个字符时,如果是相等的,比如
aa,也是一个回文串。 - 当有三个及以上字符时,比如
ababa这个字符记作串 1,把两边的a去掉,也就是bab记作串 2,可以看出只要串2是一个回文串,那么左右各多了一个a的串 1 必定也是回文串。所以当s[i]==s[j]时,自然要看dp[i+1][j-1]是不是一个回文串。
class Solution {
public int countSubstrings(String s) {
boolean[][] dp = new boolean[s.length()][s.length()];
int res = 0;
// 本题中的回文字串是连续的,要求不连续的回文串:516. 最长回文子序列
for(int j = 0; j < s.length(); j++){
for(int i = 0; i <= j; i++){
// 当只有一个字符时,比如 a 自然是一个回文串。
// 当有两个字符时,如果是相等的,比如 aa,也是一个回文串。
// 当有三个及以上字符时,比如 ababa 这个字符记作串 1,把两边的 a 去掉,也就是 bab 记作串 2,
// 可以看出只要串2是一个回文串,那么左右各多了一个 a 的串 1 必定也是回文串。
// 所以当 s[i]==s[j] 时,自然要看 dp[i+1][j-1] 是不是一个回文串。
if(s.charAt(i) == s.charAt(j) && (j - i < 2 || dp[i + 1][j - 1])){
dp[i][j] = true;
res++;
}
}
}
return res;
}
}
方法二:中心拓展法
比如对一个字符串 ababa,选择最中间的 a 作为中心点,往两边扩散,第一次扩散发现 left 指向的是 b,right 指向的也是 b,所以是回文串,继续扩散,同理 ababa 也是回文串。
这个是确定了一个中心点后的寻找的路径,然后我们只要寻找到所有的中心点,问题就解决了。
中心点一共有多少个呢?看起来像是和字符串长度相等,但你会发现,如果是这样,上面的例子永远也搜不到 abab,想象一下单个字符的哪个中心点扩展可以得到这个子串?似乎不可能。所以中心点不能只有单个字符构成,还要包括两个字符,比如上面这个子串 abab,就可以有中心点 ba 扩展一次得到,所以最终的中心点由 2 * len - 1 个,分别是 len 个单字符和 len - 1 个双字符。
如果上面看不太懂的话,还可以看看下面几个问题:
- 为什么有
2 * len - 1个中心点?aba有5个中心点,分别是a、b、c、ab、baabba有7个中心点,分别是a、b、b、a、ab、bb、ba
- 什么是中心点?
- 中心点即
left指针和right指针初始化指向的地方,可能是一个也可能是两个
- 中心点即
- 为什么不可能是三个或者更多?
- 因为 `3 个可以由 1 个扩展一次得到,4 个可以由两个扩展一次得到
class Solution {
public int countSubstrings(String s) {
int res = 0;
int n = s.length();
for(int center = 0; center < 2 * n - 1; center++){
// left和right指针和中心点的关系是?
// 首先是left,有一个很明显的2倍关系的存在,其次是right,可能和left指向同一个(偶数时),也可能往后移动一个(奇数)
// 大致的关系出来了,可以选择带两个特殊例子进去看看是否满足。
int left = center / 2, right = left + center % 2;
while(left >= 0 && right < n && s.charAt(left) == s.charAt(right)){
// 找到了一个回文串
res++;
// 向两侧拓展
left--;
right++;
}
}
return res;
}
}
这个解法也同样适用于 leetcode 5 最长回文子串,按上述代码,稍作修改,即可得到,第五题的解法:
5. 最长回文子串
难度中等6439
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
class Solution {
public String longestPalindrome(String s) {
String res = "";
int n = s.length();
for(int center = 0; center < 2 * n - 1; center++){
// left和right指针和中心点的关系是?
// 首先是left,有一个很明显的2倍关系的存在,其次是right,可能和left指向同一个(偶数时),也可能往后移动一个(奇数)
// 大致的关系出来了,可以选择带两个特殊例子进去看看是否满足。
int left = center / 2, right = left + center % 2;
while(left >= 0 && right < n && s.charAt(left) == s.charAt(right)){
// 找到了一个回文串
if(res.length() < s.substring(left, right+1).length()){
res = s.substring(left, right + 1);
}
// 向两侧拓展
left--;
right++;
}
}
return res;
}
}
2430. 对字母串可执行的最大删除数
难度困难40收藏分享切换为英文接收动态反馈
给你一个仅由小写英文字母组成的字符串 s 。在一步操作中,你可以:
- 删除 整个字符串
s,或者 - 对于满足
1 <= i <= s.length / 2的任意i,如果s中的 前i个字母和接下来的i个字母 相等 ,删除 前i个字母。
例如,如果 s = "ababc" ,那么在一步操作中,你可以删除 s 的前两个字母得到 "abc" ,因为 s 的前两个字母和接下来的两个字母都等于 "ab" 。
返回删除 s 所需的最大操作数。
示例 1:
输入:s = "abcabcdabc"
输出:2
解释:
- 删除前 3 个字母("abc"),因为它们和接下来 3 个字母相等。现在,s = "abcdabc"。
- 删除全部字母。
一共用了 2 步操作,所以返回 2 。可以证明 2 是所需的最大操作数。
注意,在第二步操作中无法再次删除 "abc" ,因为 "abc" 的下一次出现并不是位于接下来的 3 个字母。
示例 2:
输入:s = "aaabaab"
输出:4
解释:
- 删除第一个字母("a"),因为它和接下来的字母相等。现在,s = "aabaab"。
- 删除前 3 个字母("aab"),因为它们和接下来 3 个字母相等。现在,s = "aab"。
- 删除第一个字母("a"),因为它和接下来的字母相等。现在,s = "ab"。
- 删除全部字母。
一共用了 4 步操作,所以返回 4 。可以证明 4 是所需的最大操作数。
示例 3:
输入:s = "aaaaa"
输出:5
解释:在每一步操作中,都可以仅删除 s 的第一个字母。
提示:
1 <= s.length <= 4000s仅由小写英文字母组成
题解:https://leetcode.cn/problems/maximum-deletions-on-a-string/solution/xian-xing-dppythonjavacgo-by-endlesschen-gpx9/
class Solution {
/**
o(n^2) 看数据范围猜算法
每次操作结束后,剩下的还是一个子串(一个完整的字符串)
又可以对子串进行同样的操作 =>子问题 => DP
f[i] = 操作 s[i:] 所需要的最大操作次数
ans = f[0]
f[i] = f[i+j] + 1, if s[i:i+j] == s[i+j:i+2*j]
f[i] = 1 if s[i:i+j] != s[i+j:i+2*j]
两种情况取 max
重点放到怎么快速判断两个子串是否相同上。
lcp 两个后缀的最长公共前缀
lcp[i][j] = s[i:] 和 s[j:] 的最长公共前缀
s[i:i+j] == s[i+j:i + 2*j] 等价于 lcp[i][i+j] >= j
// 注意这里的最长公共前缀lcp是后缀的lcp
lcp[i][j] = lcp[i+1][j+1] + 1 (s[i] == s[j])
0 (s[i] != s[j])
*/
public int deleteString(String S) {
char[] s = S.toCharArray();
int n = s.length;
// lcp[i][j] 表示 s[i:] 和 s[j:] 的最长公共前缀(后缀的最长公共前缀)
int[][] lcp = new int[n+1][n+1];
for(int i = n-1; i >= 0; i--){
for(int j = n-1; j >= 0; j--){
if(s[i] == s[j])
lcp[i][j] = lcp[i+1][j+1] + 1;
}
}
int[] f = new int[n]; // f[i] 表示操作 s[i:] 所需要的最大操作次数
// // f[i] = max(f[i + j] + 1), i + j < n && lcp[i][i + j] >= j
for(int i = n-1; i >= 0; i--){
for(int j = 1; i + j*2 <= n; j++){
if(lcp[i][i+j] >= j)// 说明 s[i:i+j] == s[i+j:i+j*2]
f[i] = Math.max(f[i], f[i + j]);
}
f[i]++;
}
return f[0];
}
}
2376. 统计特殊整数
难度困难55
如果一个正整数每一个数位都是 互不相同 的,我们称它是 特殊整数 。
给你一个 正 整数 n ,请你返回区间 [1, n] 之间特殊整数的数目。
示例 1:
输入:n = 20
输出:19
解释:1 到 20 之间所有整数除了 11 以外都是特殊整数。所以总共有 19 个特殊整数。
示例 2:
输入:n = 5
输出:5
解释:1 到 5 所有整数都是特殊整数。
示例 3:
输入:n = 135
输出:110
解释:从 1 到 135 总共有 110 个整数是特殊整数。
不特殊的部分数字为:22 ,114 和 131 。
提示:
1 <= n <= 2 * 109
class Solution {
char s[];
int dp[][]; // i, mask 记忆化搜索不需要记忆islimit和isnum
public int countSpecialNumbers(int n) {
s = Integer.toString(n).toCharArray();
int m = s.length;
dp = new int[m][1<<10]; // [1<<10]=[1024]
for(int i = 0; i < m; i++) Arrays.fill(dp[i], -1);
//islimit初始化为true:因为初始i就是0位上的
//isNum初始化为false:因为什么数字都没填,不是数字
return f(0, 0, true, false);
}
// 返回从 i 开始填数字,i前面填的数字的集合是mask,能构造出的特殊整数的数目
// isLimit表示前面填的数字是否都是n对应位上的,
// 如果为true,那么当前位至多为(int)s[i],否则至多为9
// is_num表示前面是否填了数字(是否跳过),
// 若为ture,那么当前位可以从0开始,如果为false,那么当前位可以跳过,或者从1开始
int f(int i, int mask, boolean isLimit, boolean isNum){
if(i == s.length) //到了递归终点
return isNum ? 1 : 0;
if(!isLimit && isNum && dp[i][mask] >= 0)
return dp[i][mask];
int res = 0;
// isNum==false,若前面没有填数字(跳过了),可以继续跳过当前数位(不填数字)
// 此时这里的isLimit=false,因为此时前面填的数字不是n位对应上限,可以填0-9
if(!isNum) res = f(i + 1, mask, false, false);
// 枚举要填入的数字 d
for(int d = isNum ? 0 : 1, up = isLimit? s[i]-'0' : 9; d <= up; d++){
if((mask >> d & 1) == 0){ // d 不在 mask 中【这里的判断具体看题目要求】
res += f(i+1, mask | (1 << d), isLimit & (d == up), true);
}
}
if(!isLimit && isNum) dp[i][mask] = res;
return res;
}
}
🎉2407. 最长递增子序列 II
难度困难60
给你一个整数数组 nums 和一个整数 k 。
找到 nums 中满足以下要求的最长子序列:
- 子序列 严格递增
- 子序列中相邻元素的差值 不超过
k。
请你返回满足上述要求的 最长子序列 的长度。
子序列 是从一个数组中删除部分元素后,剩余元素不改变顺序得到的数组。
示例 1:
输入:nums = [4,2,1,4,3,4,5,8,15], k = 3
输出:5
解释:
满足要求的最长子序列是 [1,3,4,5,8] 。
子序列长度为 5 ,所以我们返回 5 。
注意子序列 [1,3,4,5,8,15] 不满足要求,因为 15 - 8 = 7 大于 3 。
示例 2:
输入:nums = [7,4,5,1,8,12,4,7], k = 5
输出:4
解释:
满足要求的最长子序列是 [4,5,8,12] 。
子序列长度为 4 ,所以我们返回 4 。
示例 3:
输入:nums = [1,5], k = 1
输出:1
解释:
满足要求的最长子序列是 [1] 。
子序列长度为 1 ,所以我们返回 1 。
提示:
1 <= nums.length <= 1051 <= nums[i], k <= 105
线段树解法的最长递增子序列,状态从j-k < j' < j 而不是0 < j' < j转移过来
class Solution {
public int lengthOfLIS(int[] nums, int k) {
for(int num : nums){
num += (int)1e4; // -104 <= nums[i] <= 104,都变成正数
int startidx = Math.max(num - k, 1);
// 查找以元素值(1,num-1)结尾的LIS的最大值
int res = 1 + query(root,1,N,startidx,num-1);
update(root,1,N,num,num,res);// 更新为前面最大值 + 1
}
// 最后返回区间最大值
return query(root,1,N,1,N);
}
class Node {
// 左右孩子节点
Node left, right;
// 当前节点值,以及懒惰标记的值
int val, add;
}
private int N = (int) 1e9;
private Node root = new Node();
public void update(Node node, int start, int end, int l, int r, int val) {
if (l <= start && end <= r) {
node.val = val;
node.add = val;
return ;
}
pushDown(node);
int mid = (start + end) >> 1;
if (l <= mid) update(node.left, start, mid, l, r, val);
if (r > mid) update(node.right, mid + 1, end, l, r, val);
pushUp(node);
}
public int query(Node node, int start, int end, int l, int r) {
if (l <= start && end <= r) return node.val;
pushDown(node);
int mid = (start + end) >> 1, ans = 0;
if (l <= mid) ans = query(node.left, start, mid, l, r);
if (r > mid) ans = Math.max(ans, query(node.right, mid + 1, end, l, r));
return ans;
}
private void pushUp(Node node) {
// 每个节点存的是当前区间的最大值
node.val = Math.max(node.left.val, node.right.val);
}
private void pushDown(Node node) {
if (node.left == null) node.left = new Node();
if (node.right == null) node.right = new Node();
if (node.add == 0) return ;
node.left.val = node.add;
node.right.val = node.add;
node.left.add = node.add;
node.right.add = node.add;
node.add = 0;
}
}
😣2458. 移除子树后的二叉树高度
难度困难30
给你一棵 二叉树 的根节点 root ,树中有 n 个节点。每个节点都可以被分配一个从 1 到 n 且互不相同的值。另给你一个长度为 m 的数组 queries 。
你必须在树上执行 m 个 独立 的查询,其中第 i 个查询你需要执行以下操作:
- 从树中 移除 以
queries[i]的值作为根节点的子树。题目所用测试用例保证queries[i]不 等于根节点的值。
返回一个长度为 m 的数组 answer ,其中 answer[i] 是执行第 i 个查询后树的高度。
注意:
- 查询之间是独立的,所以在每个查询执行后,树会回到其 初始 状态。
- 树的高度是从根到树中某个节点的 最长简单路径中的边数 。
示例 1:
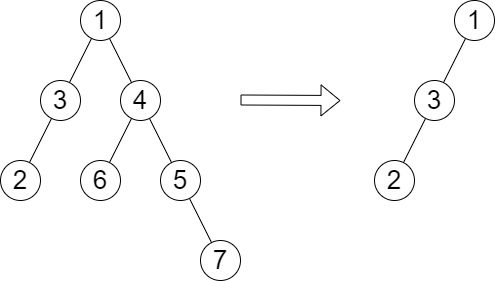
输入:root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
输出:[2]
解释:上图展示了从树中移除以 4 为根节点的子树。
树的高度是 2(路径为 1 -> 3 -> 2)。
示例 2:
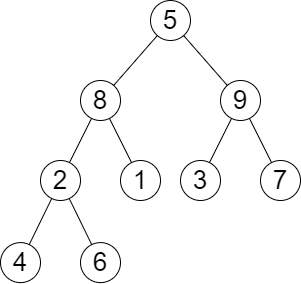
输入:root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
输出:[3,2,3,2]
解释:执行下述查询:
- 移除以 3 为根节点的子树。树的高度变为 3(路径为 5 -> 8 -> 2 -> 4)。
- 移除以 2 为根节点的子树。树的高度变为 2(路径为 5 -> 8 -> 1)。
- 移除以 4 为根节点的子树。树的高度变为 3(路径为 5 -> 8 -> 2 -> 6)。
- 移除以 8 为根节点的子树。树的高度变为 2(路径为 5 -> 9 -> 3)。
提示:
- 树中节点的数目是
n 2 <= n <= 1051 <= Node.val <= n- 树中的所有值 互不相同
m == queries.length1 <= m <= min(n, 104)1 <= queries[i] <= nqueries[i] != root.val
题解:https://leetcode.cn/problems/height-of-binary-tree-after-subtree-removal-queries/solution/liang-bian-dfspythonjavacgo-by-endlessch-vvs4/
class Solution {
/**
1. 删除一个子树时想知道其余部分的高度是多少?
既然是求树的高度,我们可以先跑一遍 DFS,求出每棵子树的高度height(这里定义为最长路径的节点数)
2. 再DFS遍历一边这棵树,同时维护当前节点深度depth,以及删除当前子树后剩余部分数的高度restH(这里定义为最长路径的边数)
*/
private Map<TreeNode, Integer> height = new HashMap<>(); // 每棵子树的高度
private int[] res; // 每个节点删除后,其余部分的最大高度(答案)
public int[] treeQueries(TreeNode root, int[] queries) {
getHeight(root);
height.put(null, 0); // 简化 dfs 的代码,这样不用写 getOrDefault
res = new int[height.size()]; // 每个节点删除后,其余部分的最大高度(答案)
dfs(root, -1, 0);
for(int i = 0; i < queries.length; i++)
queries[i] = res[queries[i]];
return queries;
}
// depth从-1开始,因为求的是边数(点数可以从0开始)
// restH删除当前节点node 剩余部分的最大高度
public void dfs(TreeNode node, int depth, int restH){
if(node == null) return;
++depth;
res[node.val] = restH; // 在递归前求出其余部分的最大高度
// 其余部分高度 = (另一部分剩余, 当前根高度 + 另一颗子树高度)
dfs(node.left, depth, Math.max(restH, depth + height.get(node.right)));
dfs(node.right, depth, Math.max(restH, depth + height.get(node.left)));
}
// dfs获得每颗子树的高度height
public int getHeight(TreeNode node){
if(node == null) return 0;
int h = 1 + Math.max(getHeight(node.left), getHeight(node.right));
height.put(node, h);
return h;
}
}
😑2478. 完美分割的方案数
难度困难25
给你一个字符串 s ,每个字符是数字 '1' 到 '9' ,再给你两个整数 k 和 minLength 。
如果对 s 的分割满足以下条件,那么我们认为它是一个 完美 分割:
s被分成k段互不相交的子字符串。- 每个子字符串长度都 至少 为
minLength。 - 每个子字符串的第一个字符都是一个 质数 数字,最后一个字符都是一个 非质数 数字。质数数字为
'2','3','5'和'7',剩下的都是非质数数字。
请你返回 s 的 完美 分割数目。由于答案可能很大,请返回答案对 109 + 7 取余 后的结果。
一个 子字符串 是字符串中一段连续字符串序列。
示例 1:
输入:s = "23542185131", k = 3, minLength = 2
输出:3
解释:存在 3 种完美分割方案:
"2354 | 218 | 5131"
"2354 | 21851 | 31"
"2354218 | 51 | 31"
示例 2:
输入:s = "23542185131", k = 3, minLength = 3
输出:1
解释:存在一种完美分割方案:"2354 | 218 | 5131" 。
示例 3:
输入:s = "3312958", k = 3, minLength = 1
输出:1
解释:存在一种完美分割方案:"331 | 29 | 58" 。
提示:
1 <= k, minLength <= s.length <= 1000s每个字符都为数字'1'到'9'之一。
class Solution {
/**
如何思考动态规划?
1、问题中有哪些变量?
分割的个数 k
字符串的长度 n
2、重新复述一遍问题,替换变量名
把一个长度为 j 的字符串,分割出 i 段的合法方案数
3、(最关键)最后一步发生了什么
分割出 一个 字串
长度为 x
且这字串是 s 的一个后缀
4、去掉最后一步,问题规模缩小了,变成什么样了?(子问题)
把一个长度为 j-x 的字符串,分割出 i-1 段的合法方案数
5、得到状态转移方程
2 == > f[i][j] 表示把 s 的前 j 个字符分割成 i 段的合法方案数
4 == > f[i][j] += f[i-1][j'] j'是第 i 段的开始下标
枚举 j'
j-j'+1 >= minLength
s[j'] 是质数 s[j] 不是质数
6、初始值和答案分别是多少
f[0][0] = 1 # 空串表示为1个方案
ans = f[k][n] # 长度为n的字符串分割成k份
(7、)优化转移
j 变大的时候,j'也在变大
==> 前缀和优化 +=过程 和 枚举
*/
private static final int MOD = (int)1e9+7;
public int beautifulPartitions(String S, int k, int minLength) {
char[] s = S.toCharArray();
int n = s.length;
if(k * minLength > n || !isPrime(s[0]) || isPrime(s[n-1]))
return 0; // 剪枝判断
// f[i][j] 表示把 s 的前 j 个字符分割成 i 段的合法方案数
// 为什么要把分割个数k放在前面,字符长度放在后面
// 套路:从小的分割个数转移到大的分割个数(区间DP思想)
int[][] f = new int[k+1][n+1];
f[0][0] = 1;
for(int i = 1; i <= k; i++){
int sum = 0;
// 循环优化:枚举的起点和终点需要给前后的子串预留出足够的长度
for(int j = i * minLength; j + (k - i) * minLength <= n; j++){
if(canPartition(s, j-minLength)) // j-minLength可以分割
sum = (sum + f[i - 1][j - minLength]) % MOD; // j'=j-minLength 双指针
if (canPartition(s, j))
f[i][j] = sum;
}
}
return f[k][n];
}
private boolean isPrime(char c) {
return c == '2' || c == '3' || c == '5' || c == '7';
}
// 判断是否可以在 j-1 和 j 之间分割(开头和末尾也算)
private boolean canPartition(char[] s, int j) {
return j == 0 || j == s.length || !isPrime(s[j - 1]) && isPrime(s[j]);
}
}
2518. 好分区的数目
难度困难27
给你一个正整数数组 nums 和一个整数 k 。
分区 的定义是:将数组划分成两个有序的 组 ,并满足每个元素 恰好 存在于 某一个 组中。如果分区中每个组的元素和都大于等于 k ,则认为分区是一个好分区。
返回 不同 的好分区的数目。由于答案可能很大,请返回对 109 + 7 取余 后的结果。
如果在两个分区中,存在某个元素 nums[i] 被分在不同的组中,则认为这两个分区不同。
示例 1:
输入:nums = [1,2,3,4], k = 4
输出:6
解释:好分区的情况是 ([1,2,3], [4]), ([1,3], [2,4]), ([1,4], [2,3]), ([2,3], [1,4]), ([2,4], [1,3]) 和 ([4], [1,2,3]) 。
示例 2:
输入:nums = [3,3,3], k = 4
输出:0
解释:数组中不存在好分区。
示例 3:
输入:nums = [6,6], k = 2
输出:2
解释:可以将 nums[0] 放入第一个分区或第二个分区中。
好分区的情况是 ([6], [6]) 和 ([6], [6]) 。
提示:
1 <= nums.length, k <= 10001 <= nums[i] <= 109
逆向思维 + 01背包:https://leetcode.cn/problems/number-of-great-partitions/solution/ni-xiang-si-wei-01-bei-bao-fang-an-shu-p-v47x/
class Solution {
/**
如果直接计算好分区的数目,我们可以用 01 背包来做,但是背包容量太大,会超时。
正难则反,我们可以反过来,计算坏分区的数目,即第一个组或第二个组的元素和小于 k 的方案数。
根据对称性,我们只需要计算第一个组的元素和小于 k 的方案数,然后乘 2 即可。
原问题就转化为 01背包:【从nums中选择若干元素,使得元素和小于k的方案数】
定义f[i][j]表示 从前 i 个数中选择了若干元素,和为 j 的方案数
分类讨论:选 or 不选
不选: f[i][j] = f[i-1][j]
选: f[i][j] = f[i-1][j - nums[i]]
因此f[i][j] = f[i-1][j] + f[i-1][j-nums[i]]
初始值f[0][0] = 1
坏分区的数目 bad = (f[n][0] + f[n][1] + ... + f[n][k-1]) * 2
答案为所有分区减去坏分区的数目 即 2^n - bad ,这里n为nums的长度
*/
private static final int MOD = (int) 1e9 + 7;
public int countPartitions(int[] nums, int k) {
var sum = 0L;
for (var x : nums) sum += x;
// 特判:如果sum(nums) < 2k,说明不存在好分区。保证第一个集合 <k 和第二个集合 >k 不会有交集
if (sum < k * 2) return 0;
var ans = 1;
var f = new int[k]; // 使用倒序循环的技巧来压缩空间
f[0] = 1;
for (var x : nums) {
ans = ans * 2 % MOD;
for (var j = k - 1; j >= x; --j)
f[j] = (f[j] + f[j - x]) % MOD;
}
for (var x : f)
ans = (ans - x * 2 % MOD + MOD) % MOD; // 保证答案非负
return ans;
}
}