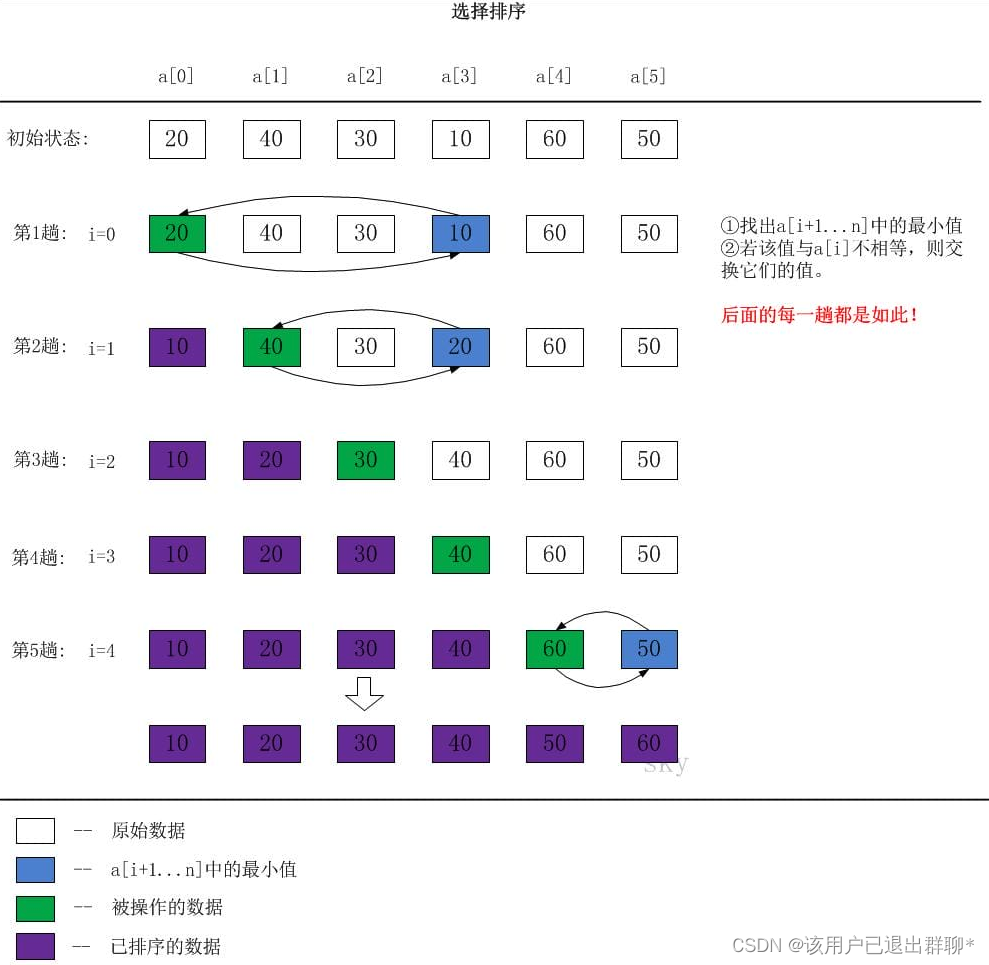
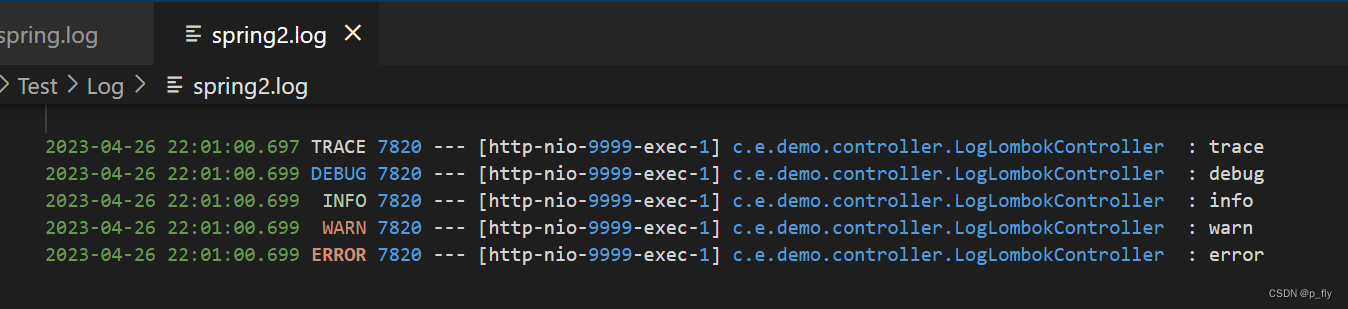
汇编小程序解析–3D立方体旋转,源代码如下,是vulture大神于1995年写的,我到现在才基本看懂。
;本程序由国外的Vulture大哥编写,并公布了源码,这个是他95年的一个作品,可以说是在当时是非常成功的!
;这个程序是巧妙的利用了坐标的不断变化,从而实现了由星星构成的箱子3D转动!
;为了尊重版权,本人未对源码注释进行翻译,这样做也可以让国内的汇编爱好者自己琢磨国外的汇编编程的思维!
;编译方法: 1 tasm 3d.asm
; 2 tlink 3d.obj
; 3 exe2bin 3d.exe 3d.com
;本程序是站长精心收集的一个很经典的3D小动画. 站长的x86汇编小站:http://www.x86asm.com
; 永久域名:http://x86asm.yeah.net
;==============================================================================;
; ;
; Assembler Program By Vulture. ;
; 3D-system example. Use the following formulas to rotate a point: ;
; ;
; Rotate around x-axis ;
; YT = Y * COS(xang) - Z * SIN(xang) / 256 ;
; ZT = Y * SIN(xang) + Z * COS(xang) / 256 ;
; Y = YT ;
; Z = ZT ;
; ;
; Rotate around y-axis ;
; XT = X * COS(yang) - Z * SIN(yang) / 256 ;
; ZT = X * SIN(yang) + Z * COS(yang) / 256 ;
; X = XT ;
; Z = ZT ;
; ;
; Rotate around z-axis ;
; XT = X * COS(zang) - Y * SIN(zang) / 256 ;
; YT = X * SIN(zang) + Y * COS(zang) / 256 ;
; X = XT ;
; Y = YT ;
; ;
; Divide by 256 coz we have multiplyd our sin values with 256 too. ;
; This example isn't too fast right now but it'll work just fine. ;
; ;
; Current Date: 6-9-95 Vulture ;
; ;
;==============================================================================;
IDEAL ; Ideal mode
P386 ; Allow 80386 instructions
JUMPS ; Tasm handles out of range jumps (rulez!:))
SEGMENT CODE ; Code segment starts
ASSUME cs:code,ds:code ; Let cs and ds point to code segment
ORG 100h ; Make a .COM file
START: ; Main program
mov ax,0013h ; Init vga
int 10h
mov ax,cs
mov ds,ax ; ds points to codesegment
mov ax,0a000h
mov es,ax ; es points to vga
lea si,[Palette] ; Set palette
mov dx,3c8h
xor al,al
out dx,al
mov dx,3c9h
mov cx,189*3
repz outsb
; === Set some variables ===
mov [DeltaX],1 ; Initial speed of rotation
mov [DeltaY],1 ; Change this and watch what
mov [DeltaZ],1 ; happens. It's fun!
mov [Xoff],256
mov [Yoff],256 ; Used for calculating vga-pos
mov [Zoff],300 ; Distance from viewer
MainLoop:
call MainProgram ; Yep... do it all... ;-)
in al,60h ; Scan keyboard
cmp al,1 ; Test on ESCAPE
jne MainLoop ; Continue if not keypressed
; === Quit to DOS ===
mov ax,0003h ; Back to textmode
int 10h
lea dx,[Credits]
mov ah,9
int 21h
mov ax,4c00h ; Return control to DOS
int 21h ; Call DOS interrupt
; === Sub-routines ===
PROC WaitVrt ; Waits for vertical retrace to reduce "snow"
mov dx,3dah
Vrt:
in al,dx
test al,8
jnz Vrt ; Wait until Verticle Retrace starts
NoVrt:
in al,dx
test al,8
jz NoVrt ; Wait until Verticle Retrace ends
ret ; Return to main program
ENDP WaitVrt
PROC UpdateAngles
; Calculates new x,y,z angles
; to rotate around
mov ax,[XAngle] ; Load current angles
mov bx,[YAngle]
mov cx,[ZAngle]
add ax,[DeltaX] ; Add velocity
and ax,11111111b ; Range from 0..255
mov [XAngle],ax ; Update X
add bx,[DeltaY] ; Add velocity
and bx,11111111b ; Range from 0..255
mov [YAngle],bx ; Update Y
add cx,[DeltaZ] ; Add velocity
and cx,11111111b ; Range from 0..255
mov [ZAngle],cx ; Update Z
ret
ENDP UpdateAngles
PROC GetSinCos
; Needed : bx=angle (0..255)
; Returns: ax=Sin bx=Cos
push bx ; Save angle (use as pointer)
shl bx,1 ; Grab a word so bx=bx*2
mov ax,[SinCos + bx] ; Get sine
pop bx ; Restore pointer into bx
push ax ; Save sine on stack
add bx,64 ; Add 64 to get cosine
and bx,11111111b ; Range from 0..255
shl bx,1 ; *2 coz it's a word
mov ax,[SinCos + bx] ; Get cosine
mov bx,ax ; Save it bx=Cos
pop ax ; Restore ax=Sin
ret
ENDP GetSinCos
PROC SetRotation
; Set sine & cosine of x,y,z
mov bx,[XAngle] ; Grab angle
call GetSinCos ; Get the sine&cosine
mov [Xsin],ax ; Save sin
mov [Xcos],bx ; Save cos
mov bx,[Yangle]
call GetSinCos
mov [Ysin],ax
mov [Ycos],bx
mov bx,[Zangle]
call GetSinCos
mov [Zsin],ax
mov [Zcos],bx
ret
ENDP SetRotation
PROC RotatePoint ; Rotates the point around x,y,z
; Gets original x,y,z values
; This can be done elsewhere
movsx ax,[Cube+si] ; si = X (movsx coz of byte)
mov [X],ax
movsx ax,[Cube+si+1] ; si+1 = Y
mov [Y],ax
movsx ax,[Cube+si+2] ; si+2 = Z
mov [Z],ax
; Rotate around x-axis
; YT = Y * COS(xang) - Z * SIN(xang) / 256
; ZT = Y * SIN(xang) + Z * COS(xang) / 256
; Y = YT
; Z = ZT
mov ax,[Y]
mov bx,[XCos]
imul bx ; ax = Y * Cos(xang)
mov bp,ax
mov ax,[Z]
mov bx,[XSin]
imul bx ; ax = Z * Sin(xang)
sub bp,ax ; bp = Y * Cos(xang) - Z * Sin(xang)
sar bp,8 ; bp = Y * Cos(xang) - Z * Sin(xang) / 256
mov [Yt],bp
mov ax,[Y]
mov bx,[XSin]
imul bx ; ax = Y * Sin(xang)
mov bp,ax
mov ax,[Z]
mov bx,[XCos]
imul bx ; ax = Z * Cos(xang)
add bp,ax ; bp = Y * SIN(xang) + Z * COS(xang)
sar bp,8 ; bp = Y * SIN(xang) + Z * COS(xang) / 256
mov [Zt],bp
mov ax,[Yt] ; Switch values
mov [Y],ax
mov ax,[Zt]
mov [Z],ax
; Rotate around y-axis
; XT = X * COS(yang) - Z * SIN(yang) / 256
; ZT = X * SIN(yang) + Z * COS(yang) / 256
; X = XT
; Z = ZT
mov ax,[X]
mov bx,[YCos]
imul bx ; ax = X * Cos(yang)
mov bp,ax
mov ax,[Z]
mov bx,[YSin]
imul bx ; ax = Z * Sin(yang)
sub bp,ax ; bp = X * Cos(yang) - Z * Sin(yang)
sar bp,8 ; bp = X * Cos(yang) - Z * Sin(yang) / 256
mov [Xt],bp
mov ax,[X]
mov bx,[YSin]
imul bx ; ax = X * Sin(yang)
mov bp,ax
mov ax,[Z]
mov bx,[YCos]
imul bx ; ax = Z * Cos(yang)
add bp,ax ; bp = X * SIN(yang) + Z * COS(yang)
sar bp,8 ; bp = X * SIN(yang) + Z * COS(yang) / 256
mov [Zt],bp
mov ax,[Xt] ; Switch values
mov [X],ax
mov ax,[Zt]
mov [Z],ax
; Rotate around z-axis
; XT = X * COS(zang) - Y * SIN(zang) / 256
; YT = X * SIN(zang) + Y * COS(zang) / 256
; X = XT
; Y = YT
mov ax,[X]
mov bx,[ZCos]
imul bx ; ax = X * Cos(zang)
mov bp,ax
mov ax,[Y]
mov bx,[ZSin]
imul bx ; ax = Y * Sin(zang)
sub bp,ax ; bp = X * Cos(zang) - Y * Sin(zang)
sar bp,8 ; bp = X * Cos(zang) - Y * Sin(zang) / 256
mov [Xt],bp
mov ax,[X]
mov bx,[ZSin]
imul bx ; ax = X * Sin(zang)
mov bp,ax
mov ax,[Y]
mov bx,[ZCos]
imul bx ; ax = Y * Cos(zang)
add bp,ax ; bp = X * SIN(zang) + Y * COS(zang)
sar bp,8 ; bp = X * SIN(zang) + Y * COS(zang) / 256
mov [Yt],bp
mov ax,[Xt] ; Switch values
mov [X],ax
mov ax,[Yt]
mov [Y],ax
ret
ENDP RotatePoint
PROC ShowPoint
; Calculates screenposition and
; plots the point on the screen
mov ax,[Xoff] ; Xoff*X / Z+Zoff = screen x
mov bx,[X]
imul bx
mov bx,[Z]
add bx,[Zoff] ; Distance
idiv bx
add ax,[Mx] ; Center on screen
mov bp,ax
mov ax,[Yoff] ; Yoff*Y / Z+Zoff = screen y
mov bx,[Y]
imul bx
mov bx,[Z]
add bx,[Zoff] ; Distance
idiv bx
add ax,[My] ; Center on screen
mov bx,320
imul bx
add ax,bp ; ax = (y*320)+x
mov di,ax
mov ax,[Z] ; Get color from Z
add ax,100d ; (This piece of code could be improved)
mov [byte ptr es:di],al ; Place a dot with color al
mov [Erase+si],di ; Save position for erase
ret
ENDP ShowPoint
PROC MainProgram
call UpdateAngles ; Calculate new angles
call SetRotation ; Find sine & cosine of those angles
xor si,si ; First 3d-point
mov cx,MaxPoints
ShowLoop:
call RotatePoint ; Rotates the point using above formulas
call ShowPoint ; Shows the point
add si,3 ; Next 3d-point
loop ShowLoop
call WaitVrt ; Wait for retrace
xor si,si ; Starting with point 0
xor al,al ; Color = 0 = black
mov cx,MaxPoints
Deletion:
mov di,[Erase+si] ; di = vgapos old point
mov [byte ptr es:di],al ; Delete it
add si,3 ; Next point
loop Deletion
ret
ENDP MainProgram
; === DATA ===
Credits DB 13,10,"Code by Vulture / Outlaw Triad",13,10,"$"
Label SinCos Word ; 256 values
dw 0,6,13,19,25,31,38,44,50,56
dw 62,68,74,80,86,92,98,104,109,115
dw 121,126,132,137,142,147,152,157,162,167
dw 172,177,181,185,190,194,198,202,206,209
dw 213,216,220,223,226,229,231,234,237,239
dw 241,243,245,247,248,250,251,252,253,254
dw 255,255,256,256,256,256,256,255,255,254
dw 253,252,251,250,248,247,245,243,241,239
dw 237,234,231,229,226,223,220,216,213,209
dw 206,202,198,194,190,185,181,177,172,167
dw 162,157,152,147,142,137,132,126,121,115
dw 109,104,98,92,86,80,74,68,62,56
dw 50,44,38,31,25,19,13,6,0,-6
dw -13,-19,-25,-31,-38,-44,-50,-56,-62,-68
dw -74,-80,-86,-92,-98,-104,-109,-115,-121,-126
dw -132,-137,-142,-147,-152,-157,-162,-167,-172,-177
dw -181,-185,-190,-194,-198,-202,-206,-209,-213,-216
dw -220,-223,-226,-229,-231,-234,-237,-239,-241,-243
dw -245,-247,-248,-250,-251,-252,-253,-254,-255,-255
dw -256,-256,-256,-256,-256,-255,-255,-254,-253,-252
dw -251,-250,-248,-247,-245,-243,-241,-239,-237,-234
dw -231,-229,-226,-223,-220,-216,-213,-209,-206,-202
dw -198,-194,-190,-185,-181,-177,-172,-167,-162,-157
dw -152,-147,-142,-137,-132,-126,-121,-115,-109,-104
dw -98,-92,-86,-80,-74,-68,-62,-56,-50,-44
dw -38,-31,-25,-19,-13,-6
Label Cube Byte ; The 3d points
c = -35 ; 5x*5y*5z (=125) points
rept 5
b = -35
rept 5
a = -35
rept 5
db a,b,c
a = a + 20
endm
b = b + 20
endm
c = c + 20
endm
Label Palette Byte ; The palette to use
db 0,0,0 ; 63*3 gray-tint
d = 63
rept 63
db d,d,d
db d,d,d
db d,d,d
d = d - 1
endm
X DW ? ; X variable for formula
Y DW ?
Z DW ?
Xt DW ? ; Temporary variable for x
Yt DW ?
Zt DW ?
XAngle DW 0 ; Angle to rotate around x
YAngle DW 0
ZAngle DW 0
DeltaX DW ? ; Amound Xangle is increased each time
DeltaY DW ?
DeltaZ DW ?
Xoff DW ?
Yoff DW ?
Zoff DW ? ; Distance from viewer
XSin DW ? ; Sine and cosine of angle to rotate around
XCos DW ?
YSin DW ?
YCos DW ?
ZSin DW ?
ZCos DW ?
Mx DW 160 ; Middle of the screen
My DW 100
MaxPoints EQU 125 ; Number of 3d Points
Erase DW MaxPoints DUP (?) ; Array for deletion screenpoints
ENDS CODE ; End of codesegment
END START ; The definite end.... :)
; You may use this code in your own productions but
; give credit where credit is due. Only lamers steal
; code so try to create your own 3d-engine and use
; this code as an example.
; Thanx must go to Arno Brouwer and Ash for releasing
; example sources.
;
; Ciao dudoz,
;
; Vulture / Outlaw Triad
首先,学习一下图形变换的基础知识。
1. 向量绕坐标轴或者原点旋转
旋转的时候,向量的长度不变,方向发生变化。
由二维向量绕原点旋转得知 :
x1 = r * cos a
y1 = r * sin a
得出:
x2 = r * cos ( a + b) = r * cos a * cos b - r * sin a * sin b = x1 * cos b - y1 * sinb
y2 = r * sin ( a + b) = r * sin a * cos b + r * cos a * sin b = x1 * sinb + y1 * cosb
由此得出以下旋转公式(注意矩阵乘法不满足结合律,故两个向量的顺序不能颠倒):
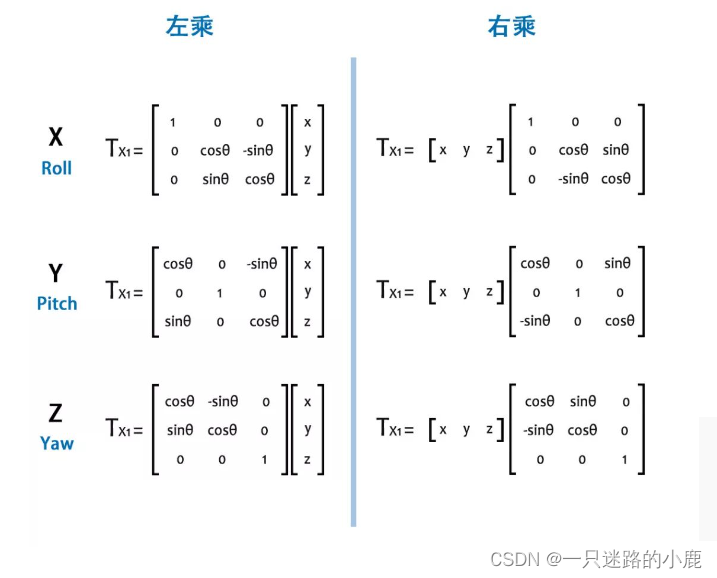



注意,网上很多资料都是引用的下图的公式,到底哪个是对的,我需要再考虑一下。

2. 向量移动
平移得时候,图像或者向量的长度和方向不变,但是位置发生变化。
由:
x2 = x1 + a
y2 = y1 + b
z2 = z1 + c
得如下平移公式:

注意:平移公式维度从3维上升到4维,因为只有这样,才可以用矩阵乘法表示向量的平移操作,否则,只能用加法来表示向量平移操作。同时,因为平移操作上升了矩阵计算的维度,所以其他的操作,比如旋转、缩放也是用4维矩阵乘法来实现的,这样所有的操作和计算就实现了数学形式上的统一。这也就是齐次坐标的来源。
3. 向量缩小放大
向量或者图像缩放,可以按照几个坐标方向的系数分别缩放,缩放时。
由:
x2 = x1 * a
y2 = y1 * b
z2 = z1 * c
可得如下公式:
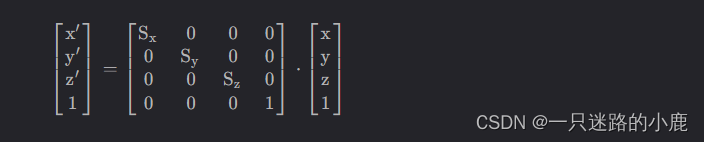
实际上,图像的几何变换通常不是单一的,也就是说经常性的缩放、旋转、平移一起变换。例如先放大2倍,然后旋转45度,然后再缩小0.5倍。那么就可以表示成矩阵乘法串接的形式:
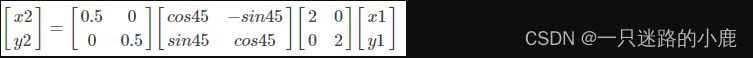
4. 绕任意点的二维旋转
首先将旋转点移动到原点处,执行如上面所描述的绕原点的旋转,再将旋转点移回到原来的位置。
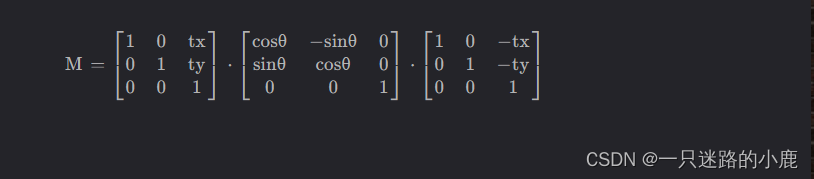
4. 绕任意轴的三维旋转
这种旋转又分为2种情况:
旋转轴平行于坐标轴。
将旋转轴平移至与坐标轴重合,旋转,步骤1的逆过程。
旋转住不平行于坐标轴。
将旋转轴平移至原点(如果经过原点则此步骤可省略)
将旋转轴旋转角度c,与z轴重合,向量映射至 XOY 平面
将旋转轴旋转b,旋转至于X轴重合,向量映射至x轴上
绕 X轴旋转 a度
执行步骤3的逆过程
执行步骤2的逆过程
执行步骤1的逆过程
其中,a,b,c分别为向量和x,y,z轴的夹角。
结合此文章可以更明确的理解上述公式:
图像旋转变换