深度学习 -- pytorch 计算图与动态图机制 autograd与逻辑回归模型

news2024/9/22 0:39:18

前言

pytorch中的动态图机制是pytorch这门框架的优势所在，阅读本篇博客可以使我们对动态图机制以及静态图机制有更直观的理解，同时在博客的后半部分有关于逻辑回归的知识点，并且使用pytorch中张量以及张量的自动求导进行构建逻辑回归模型。

计算图

计算图是用来描述运算的有向无环图

计算图有两个主要元素:节点（Node）和边（Edge）

节点表示数据，如向量，矩阵，张量，边表示运算，如加减乘除卷积等。

用计算图表示：y = (x+w)*(w+1)

  • a = x + w
  • b = w + 1
  • y = a * b

采用计算图进行计算的好处

它不仅仅能够让我们的运算更加简洁，更重要的作用是使得梯度求导更方便

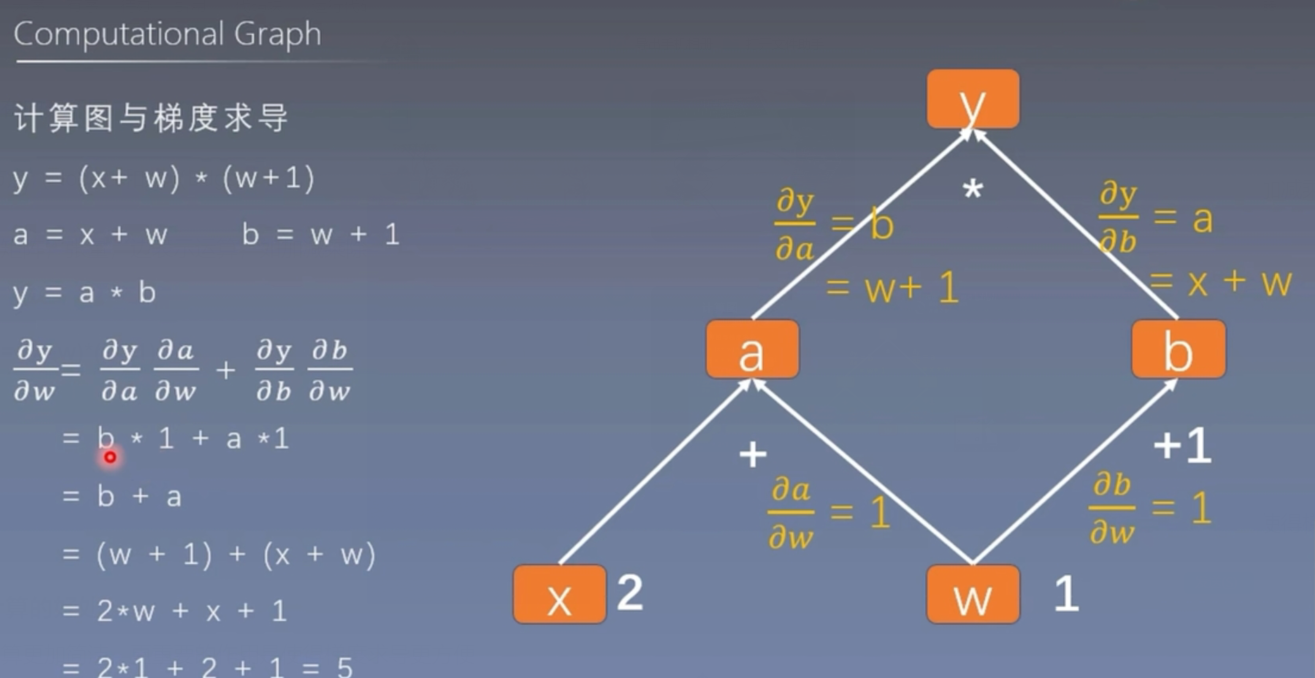
在这里插入图片描述

我们可以用pytorch模拟这个过程

import torch

# 创建w和x两个节点
w = torch.tensor([1.],requires_grad=True)
x = torch.tensor([2.],requires_grad=True)

a = torch.add(w,x)
b = torch.add(w,1)
y = torch.mul(a,b)

y.backward()  # 调用反向传播 梯度求导
print(w.grad)  # tensor([5.])

叶子节点

用户创建的节点称为叶子节点
上述代码创建的w和x 就是叶子节点
is_leaf:知识张量是否为叶子结点

  • 只有叶子节点能输出梯度 因为非叶子节点在计算之后的梯度会自动回收
import torch

# 创建w和x两个节点
w = torch.tensor([1.],requires_grad=True)
x = torch.tensor([2.],requires_grad=True)

a = torch.add(w,x)
b = torch.add(w,1)
y = torch.mul(a,b)

# y.backward()  # 调用反向传播 梯度求导
# print(w.grad)
print(w.is_leaf,x.is_leaf,a.is_leaf,b.is_leaf,y.is_leaf)

输出：

True True False False False

输出非叶子节点的梯度的方法

在非叶子节点创建之后执行.retain_grad()命令

import torch

# 创建w和x两个节点
w = torch.tensor([1.],requires_grad=True)
x = torch.tensor([2.],requires_grad=True)

a = torch.add(w,x)
a.retain_grad()
b = torch.add(w,1)
y = torch.mul(a,b)

y.backward()  # 调用反向传播 梯度求导
# print(w.grad)
# print(w.is_leaf,x.is_leaf,a.is_leaf,b.is_leaf,y.is_leaf)
print(w.grad,a.grad)  # tensor([5.]) tensor([2.])
  • grad_fn:记录创建该张量时所用的方法
print(y.grad_fn,a.grad_fn,b.grad_fn)
# 输出：
# <MulBackward0 object at 0x0000026458E32CA0>
# <AddBackward0 object at 0x0000026458DA2670> 
# <AddBackward0 object at 0x0000026458DA20D0>

动态图与静态图

在计算图中，根据搭建方式的不同，可以将计算图分为动态图和静态图。

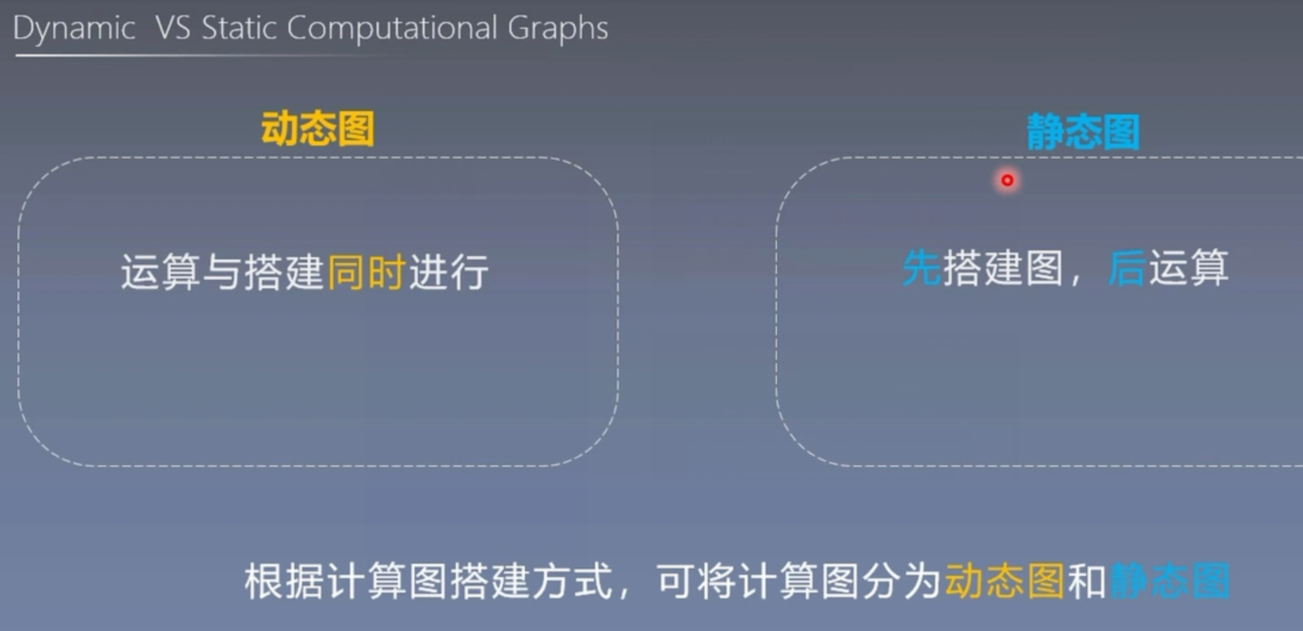
在这里插入图片描述

动态图的优点：灵活、易调节
静态图的优点：高效
静态图的缺点：不灵活

pytorch中的自动求导系统autograd

torch.autograd

梯度的计算在模型训练中是十分重要的，然而梯度的计算十分的繁琐，所以pytorch提供了一套自动求导的系统，我们只需要手动搭建计算图，pytorch就能帮我们自动求导。

  • torch.autograd.backward

功能：自动求取梯度

在这里插入图片描述

tensors:用于求导的张量，如loss
retain_graph:保存计算图
create_graph:创建导数计算图，用于高阶求导
grad_tensors：多梯度权重

张量中的backward()方法实际就是调用了atuograd.backward()方法

y.backward(retain_graph=True)

backward方法中的参数retain_graph，是保存计算图的意思，如果想要连续进行两次反向传播，这个参数必须设置为True，因为如果用默认的false，执行完第一次之后pytorch会把计算图自动释放掉。

grad_tensors的使用

import torch

# 创建w和x两个节点
w = torch.tensor([1.],requires_grad=True)
x = torch.tensor([2.],requires_grad=True)

a = torch.add(w,x)
a.retain_grad()
b = torch.add(w,1)
y0 = torch.mul(a,b)
y1 = torch.add(a,b)
loss = torch.cat([y0,y1],dim=0)
grad_tensors = torch.tensor([1.,1.])
loss.backward(gradient=grad_tensors)
print(w.grad)  # tensor([7.])
  • torch.atuograd.grad

功能：求取梯度

在这里插入图片描述

outputs:用于求导的张量，如loss
inputs:需要梯度的张量
create_graph：创建导数计算图，用于高阶求导
retain_graph:保存计算图
grad_outputs:多梯度权重

高阶导数

import torch
x = torch.tensor([3.],requires_grad=True)
y = torch.pow(x,2) # y = x**2

# 1阶求导 对y进行求导
grad_1 = torch.autograd.grad(y,x,create_graph=True) # create_graph：创建导数计算图，用于高阶求导
print(grad_1)  # (tensor([6.], grad_fn=<MulBackward0>),)


# 2阶求导
grad_2 = torch.autograd.grad(grad_1[0],x)
print(grad_2) # (tensor([2.]),)

注意：
1、梯度不自动清零

import torch
w = torch.tensor([1.],requires_grad=True)
x = torch.tensor([2.],requires_grad=True)

for i in range(4):
    a = torch.add(w,x)
    b = torch.add(w,1)
    y = torch.mul(a,b)

    y.backward()
    print(w.grad)

输出：

tensor([5.])
tensor([10.])
tensor([15.])
tensor([20.])

说明梯度是不断累加的，原位操作 .grad.zero_() 就能解决这个问题

2、依赖于叶子结点的结点的require_grad都是True

import torch

# 创建w和x两个节点
w = torch.tensor([1.],requires_grad=True)
x = torch.tensor([2.],requires_grad=True)

a = torch.add(w,x)
a.retain_grad()
b = torch.add(w,1)
y0 = torch.mul(a,b)
y1 = torch.add(a,b)
loss = torch.cat([y0,y1],dim=0)
grad_tensors = torch.tensor([1.,1.])
loss.backward(gradient=grad_tensors)
print(a.requires_grad,b.requires_grad,y0.requires_grad,y1.requires_grad)
# True True True True

3、叶子结点不可执行in-place操作（原位操作）

import torch

# 创建w和x两个节点
w = torch.tensor([1.],requires_grad=True)
x = torch.tensor([2.],requires_grad=True)

a = torch.add(w,x)
a.retain_grad()
b = torch.add(w,1)
y0 = torch.mul(a,b)
y1 = torch.add(a,b)
w.add_(1)

报错信息：

    w.add_(1)
RuntimeError: a leaf Variable that requires grad is being used in an in-place operation.

原位操作：在原始地址上直接进行改变

逻辑回归

逻辑回归模型是线性的二分类模型
模型表达式：
y = f(WX + b)
f(x) = 1/(1+e**-x)

f(x) 称为Sigmoid函数，也称为logistic函数

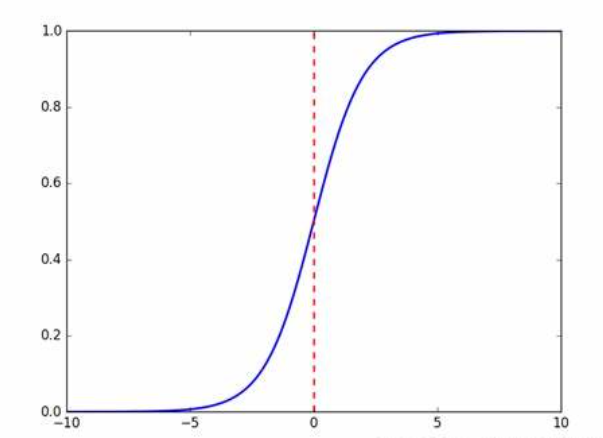
在这里插入图片描述

这样的函数我们通过设定一个阈值来进行二分类的工作

比如：当y的值小于等于0>=0.5 则最终输出1，反之则输出0。

在这里插入图片描述
线性回归是分析自变量x与因变量y(标量)之间的关系的方法
逻辑回归是分析自变量x与因变量y(概率)之间的关系的方法

pytorch中构建逻辑回归模型

import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np


# 步骤1 生成数据
sample_nums = 100
mean_value = 1.7
bias = 1
n_data = torch.ones(sample_nums,2)
x0 = torch.normal(mean_value*n_data,1)+bias     # 类别0的数据 shape=(100,2)
y0 = torch.zeros(sample_nums)           # 类别0的数据 shape=(100，1)
x1 = torch.normal(-mean_value*n_data,1)+bias # 类别1的数据 shape(100,2)
y1 = torch.ones(sample_nums)            # 类别为1 标签 shape(100,1)
train_x = torch.cat((x0,x1),0)
train_y = torch.cat((y0,y1),0)

# 步骤2 选择模型
class LR(nn.Module):
    def __init__(self):
        super(LR,self).__init__()
        self.features = nn.Linear(2,1)
        self.sigmoid = nn.Sigmoid()

    def forward(self,x):
        x = self.features(x)
        x = self.sigmoid(x)
        return x

lr_net = LR() # 实例化逻辑回归模型

# 步骤3 选择损失函数
loss_fn = nn.BCELoss() # 交叉熵

# 步骤4 选择损失函数
lr = 0.01  # 学习率
optimizer = torch.optim.SGD(lr_net.parameters(),lr=lr,momentum=0.9)

# 步骤5 模型训练
for interation in range(1000):
    # 前向传播
    y_pred = lr_net(train_x)

    # 计算损失
    loss = loss_fn(y_pred.squeeze(),train_y)

    # 反向传播
    loss.backward()

    # 更新参数
    optimizer.step()

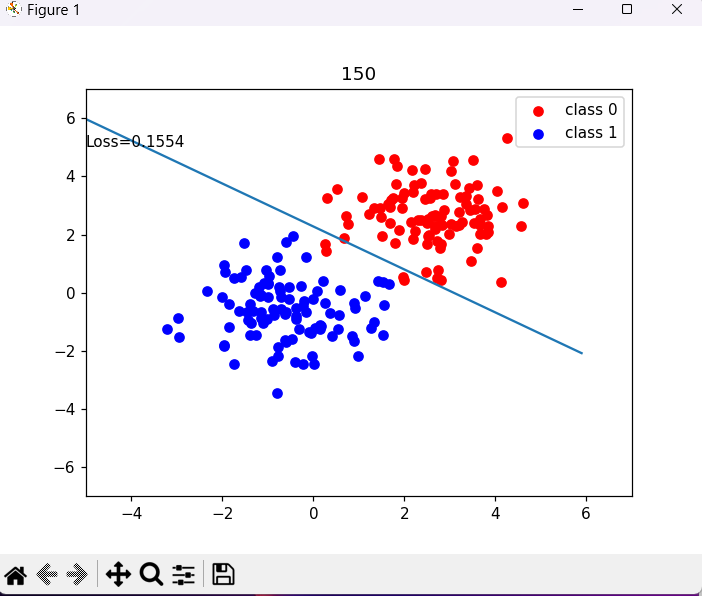
    # 绘图
    if interation % 50==0:

        mask = y_pred.ge(0.5).float().squeeze() # 以0.5为阈值进行分类
        correct = (mask == train_y).sum()
        acc = correct.item()/train_y.size(0)

        plt.scatter(x0.data.numpy()[:,0],x0.data.numpy()[:,1],c="r",label="class 0")
        plt.scatter(x1.data.numpy()[:,0],x1.data.numpy()[:,1],c="b",label="class 1")

        w0,w1 = lr_net.features.weight[0]
        w0,w1 = float(w0.item()),float(w1.item())
        plot_b = float(lr_net.features.bias[0].item())
        plot_x = np.arange(-6,6,0.1)
        plot_y = (-w0*plot_x - plot_b)/w1

        plt.xlim(-5,7)
        plt.ylim(-7,7)
        plt.plot(plot_x,plot_y)

        plt.text(-5,5,'Loss=%.4f'%loss.data.numpy())
        plt.title(interation)

        plt.legend()

        plt.show()

        if acc > 0.99:
            break

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/465429.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Springboot 自动装配流程分析

Springboot 自动装配流程分析

目录 1.基础知识&#xff1a; 2.具体代码执行流程 3.流程总结&#xff1a; 4.参考文章&#xff1a; 1.基础知识&#xff1a; springboot的自动装配是利用了spring IOC容器创建过程中的增强功能&#xff0c;即BeanFactoryPostProcessor&#xff0c; 其中的ConfigurationCla…
阅读更多...
【JavaEE】SpringBoot的日志

【JavaEE】SpringBoot的日志

目录 日志作用 SpringBoot日志框架 日志打印 日志级别 类型 作用 修改级别 日志永久化 配置日志文件目录 配置日志文件名 简化日志打印和永久化——lombok 日志作用 问题定位&#xff1a;可以帮助开发人员快速找到问题出现的位置系统监控&#xff1a;可以把系统的运…
阅读更多...
你不知道的node.js小知识——使用nvm管理node版本及node与npm版本对应关系详解

你不知道的node.js小知识——使用nvm管理node版本及node与npm版本对应关系详解

一、下载和安装nvm管理包 &#xff08;1&#xff09;下载链接 https://github.com/coreybutler/nvm-windows/releases (我选的是nvm-setup.exe) &#xff08;2&#xff09;解压安装 &#xff08;2次选择文件要安装的目录 第一次是nvm 第二次是node.js&#xff09; &#xff08;…
阅读更多...
01.DolphinScheduler集群搭建

01.DolphinScheduler集群搭建

文章目录 关于Apache DolphinScheduler简介特性简单易用丰富的使用场景High ReliabilityHigh Scalability 软硬件环境建议配置1. Linux 操作系统版本要求2. 服务器建议配置生产环境 3. 网络要求4. 客户端 Web 浏览器要求 官网地址 单机部署(没啥用)前置准备工作启动 DolphinSch…
阅读更多...
J - Playing in a Casino

J - Playing in a Casino

题意&#xff1a;相当于比大小的赌博计算赌徒一共需要支出多少赌资 比大小的规则很简单&#xff0c;是 在这个游戏中&#xff0c;有一个套牌由n卡。每张卡都有m数字写在上面。每个n玩家从一副牌中只收到一张牌。 然后所有玩家成对玩&#xff0c;每对玩家只玩一次。因此&#x…
阅读更多...
SpringBoot 中 4 种常用的数据库访问方式

SpringBoot 中 4 种常用的数据库访问方式

SpringBoot 中常用的数据库访问方式主要有以下几种&#xff1a; SpringBoot 是一个非常流行的 Java 开发框架&#xff0c;它提供了大量的开箱即用的功能&#xff0c;包括数据库访问。在开发过程中&#xff0c;我们经常需要使用数据库&#xff0c;因此选择一种合适的数据库访问…
阅读更多...
Day2_vue集成elementUI完善布局

Day2_vue集成elementUI完善布局

上一节&#xff0c;实现了从O到vue页面主体框架的搭建&#xff0c;这一节补充完善搜索框&#xff1b;新增、删除、导入、导出等按钮&#xff1b;表格设置&#xff1b;分页&#xff1b;面包屑的实现&#xff01; 目录 搜索框 新增删除、导入、导出按钮 表格设置 设置边框&a…
阅读更多...
记录安装Nodejs和HBuilderX搭建、部署微信小程序开发环境（一）

记录安装Nodejs和HBuilderX搭建、部署微信小程序开发环境（一）

文章目录 1 前言2 注册小程序账号3 安装微信开发者工具4 安装Nodejs和HBuilderX4.1 windows用户安装Nodejs4.2 macos/linux用户安装Nodejs4.3 安装HBuilder X 5 创建项目5.1 新建一个项目5.2 进行基本配置 6 HBuilderX同步微信开发者工具6.1 打开服务端口6.2 调用微信开发者工具…
阅读更多...
PHP初识

PHP初识

php简介 PHP全称超文本预处理语言&#xff0c;是在服务器端执行的脚本语言&#xff0c;是一种简单的&#xff0c;面向对象的开源脚本语言PHP脚本可以让Web开发人员快速的书写动态生成的网页 PHP脚本以<?php开始&#xff0c;以?>结束 <?php echo "hello world&…
阅读更多...
Visual Studio调试代码教学

Visual Studio调试代码教学

本篇博客主要讲解程序员最应该掌握的技能之一——调试。我个人认为&#xff0c;学习编程&#xff0c;有2件事情非常重要&#xff0c;一是画图&#xff0c;一是调试。下面我会以Visual Studio 2022为例&#xff08;VS的其他版本大同小异&#xff09;&#xff0c;演示如何调试一个…
阅读更多...
测试开发实战项目 | 搭建Pytest接口自动化框架

测试开发实战项目 | 搭建Pytest接口自动化框架

一、预研背景 目前系统研发多为前后端分离&#xff0c;当后端接口研发完成后&#xff0c;可以不依赖前端界面通过接口测试提前发现问题并解决。同时由于软件迭代周期不断缩短&#xff0c;开发新功能后又担心影响原有功能&#xff0c;可以通过接口自动化进行原有功能快速回归测…
阅读更多...
spi，iic，uart，pcie区别

spi，iic，uart，pcie区别

一、spi SPI 是英语Serial Peripheral interface的缩写&#xff0c;顾名思义就是串行外围设备接口&#xff0c;是同步传输协议&#xff0c;特征是&#xff1a;设备有主机&#xff08;master&#xff09;和从机&#xff08;slave&#xff09;的区分&#xff0c;主机在通讯时发送…
阅读更多...
分治与减治算法实验： 排序中减治法的程序设计

分治与减治算法实验： 排序中减治法的程序设计

目录 前言 实验内容 实验目的 实验分析 实验过程 流程演示 写出伪代码 实验代码 代码详解 运行结果 总结 前言 本文介绍了算法实验排序中减治法的程序设计。减治法是一种常用的算法设计技术&#xff0c;它通过减少问题的规模来求解问题。减治法可以应用于排序问题&…
阅读更多...
mysql数据库自动备份

mysql数据库自动备份

前言 服务器中数据库的数据是最重要的东西,如果因为某些情况导致数据库数据错误,数据错乱或数据库崩溃,这时一定要及时的修复,但如果数据丢失或数据没法用了,这时就要回滚数据了,而这时就需要我们经常的备份数据库的数据 正文 一般别人都会推荐使用Navicat来备份和连接数据库…
阅读更多...
Kafka时间轮(TimerWheel)--算法简介

Kafka时间轮(TimerWheel)--算法简介

一、简介 一个简单的时间轮是一个定时器任务桶的循环列表。 让u作为时间单位。尺寸为n的时间轮有n个桶&#xff0c;可以在n*u的时间间隔内保存定时器任务。每个bucket保存属于相应时间范围的计时器任务。 在开始时&#xff0c; 第一个桶保存[0&#xff0c;u&#xff09;的任务…
阅读更多...
第7章 “字典”

第7章 “字典”

1.字典简介 字典是什么&#xff1f; 解答&#xff1a;与集合类似&#xff0c;也是一种存储唯一值的数据结构&#xff0c;但它是以键值对的形式来存储。(键值对是最重要的特性)在Es6中新增了字典&#xff0c;名为Map字典的常用操作&#xff1a;增删改查 const map new Map()/…
阅读更多...
使用PY003基于外部中断+定时器的方式实现NEC红外解码

使用PY003基于外部中断+定时器的方式实现NEC红外解码

写在前边 最近项目用到一款遥控器是38K红外载波,NEC协议的&#xff0c;找了很多帖子有看到用外部中断下降沿判断&#xff08;但可惜判定数据的方式是while在外部中断里面死等的&#xff09;&#xff0c;有看到用100us定时器定时刷来判断&#xff0c;感觉都不太适合用在我这个工…
阅读更多...
基于MATLAB实现WSN（无线传感器网络）的LEACH（低能耗自适应集群层次结构）（Matlab代码实现）

基于MATLAB实现WSN（无线传感器网络）的LEACH（低能耗自适应集群层次结构）（Matlab代码实现）

目录 &#x1f4a5;1 概述 &#x1f4da;2 运行结果 &#x1f389;3 参考文献 &#x1f468;‍&#x1f4bb;4 Matlab代码 &#x1f4a5;1 概述 低能耗自适应集群层次结构&#xff08;“LEACH”&#xff09;是一种基于 TDMA 的 MAC 协议&#xff0c;它与无线传感器网络 &a…
阅读更多...
[2018.09.25][Sourceinsight]4.0配置

[2018.09.25][Sourceinsight]4.0配置

1 字体放大 (1)panel fonts: option,preference,colors&font (2)code fonts: option,file type options 2 修改默认字体 Alt y 3 显示行号 点击菜单栏View->Line Numbers 4 破解 https://blog.csdn.net/biubiuibiu/article/details/78044232 5 全局搜索字…
阅读更多...
在Spring Boot微服务使用knife4j发布后端API接口

在Spring Boot微服务使用knife4j发布后端API接口

记录&#xff1a;422 场景&#xff1a;在Spring Boot微服务上&#xff0c;应用knife4j发布后端API接口&#xff0c;辅助开发与调试。 版本&#xff1a;JDK 1.8,Spring Boot 2.6.3,knife4j-3.0.3,springfox-swagger2-3.0.0。 Knife4j: 是一个集Swagger2 和 OpenAPI3为一体的增…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023