系列文章目录
《后向投影算法(BPA)-SAR成像算法系列(二)》
文章目录
前言
一、成像场景设置
1.1 扫描模式
条带模式
聚束模式
1.2 几何构型
正侧视
斜视
1.3 成像坐标选择
固定场景直角坐标系
沿视线直角坐标系
数据获取面直角坐标系
数据获取面极坐标系
二、 BP算法
三、仿真结果
3.1.条带+正侧视+固定场景直角坐标系
3.2 聚束+斜视+固定场景直角坐标系
3.3 聚束+斜视+沿视线直角坐标系
3.4 聚束+斜视+数据获取面直角坐标系
3.5 聚束+斜视+数据获取面极坐标系
总结
前言
在CSDN写的第一篇文章是关于SAR的,到目前已有512天,粉丝朋友对我写的SAR相关文章的认可是我坚持写下去的动力。看评论区有部分粉丝说我写SAR方面的内容看得很过瘾,但是不够看,我很是高兴。今后我会在保证文章质量的前提下持续更新SAR相关的知识,但是博主本身有自身研究要开展,更新速度可能会比较慢,望各位理解。现在进入正题:
本文属于SAR成像算法系列文章,且为后向投影算法的续集。前面介绍了各种SAR成像算法,并没有分析不同扫描模式、几何构型以及成像坐标系下的成像规律。本文基于后向投影算法(BP),分析不同扫描模式、不同几何构型以及不同成像坐标系下的成像规律。下面具体介绍:
一、成像场景设置
1.1 扫描模式
SAR雷达工作模式主要由天线的扫描模式决定,按天线扫描模式,SAR工作模式可分为:条带模式、聚束模式、滑聚模式等,其中滑聚模式介于条带模式与聚束模式之间。本文主要介绍条带模式与聚束模式。
-
条带模式
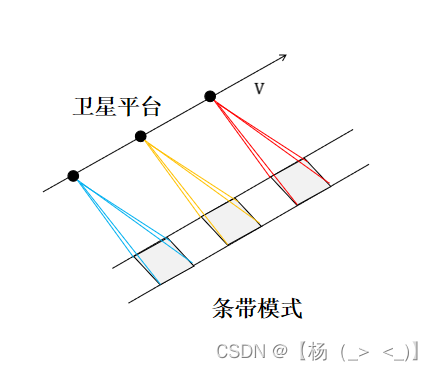
雷达天线波束指向相对于飞行平台方向保持固定,并随平台的移动在地面照射出一个与航迹平行的带状区域,此时同距离处目标的多普勒历程基本一致,只是时延不同,对应的信号模型为:
距离维脉冲压缩后信号为:
从上述表达式可以看出,距离脉压后不同方位时刻信号能量沿着
集中分布,该曲线也为距离徙动曲线,沿着这条曲线,信号可以表示为:
沿着这条曲线做相干累加,即可得到坐标下的SAR值:
-
聚束模式
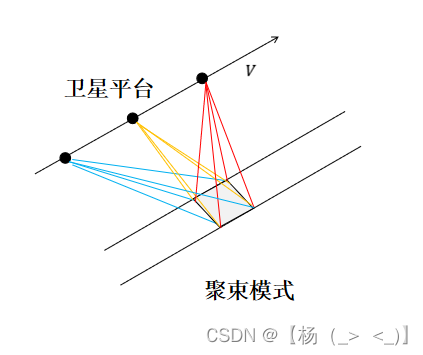
雷达天线始终指向固定的成像区域,通过雷达视角的移动使得目标的合成孔径时间极大增加,且不受限于天线波束宽度,由于整个信号采样时间,天线波束始终照射目标区域,同距离处目标的多普勒历程并不一致,对应的信号模型如下:
与条带模式相比,聚束模式的方位合成时间覆盖整个采样时段,所以最后做相干累加的时间范围为整个采样时间范围,其他步骤一致,就不赘续。
1.2 几何构型
-
正侧视
、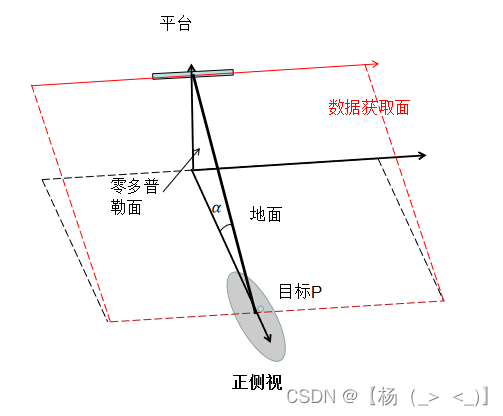
上图是正侧视的几何构型, 正侧视包含正视与侧视两个含义:正视表明天线波束中心指向位于零多普勒面(垂直于航迹的平面);侧视表明天线波束中心指向不位于平台轨迹垂直面上(即下面介绍的不为90°)。
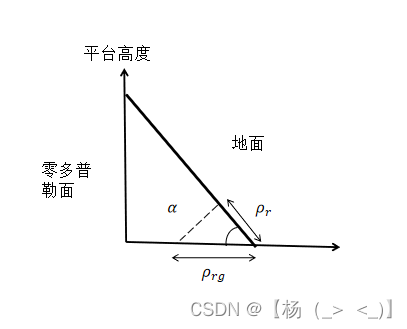
上图是零多普勒面视图,为雷达视线与地面的夹角,一般雷达所测距离为雷达视线距离,雷达测距分辨率
与雷达发射脉冲带宽有关,一般是一个固定值,当
变化时,投影到地面的距离分辨率
也变化,其与实际距离分辨率关系如下:
从上述表达式可以看出,当为90°时,对应的地距分辨率将为无穷大,此时成像所成像地距维度将会模糊,这也是SAR成像中需要雷达视线与地面需要一些夹角的原因,也是正侧视场景的设计依据。
-
斜视

上图是斜视的几何构型,与正侧视相比,斜视情况下,天线波束中心/雷达视线方向与飞行平台航迹并不垂直,存在一定的夹角,该角的余角称为斜视角(有的也认为该角为斜视角)。当夹角小于90°时,则认为是前视模式,当大于90°时,则认为是后视模式。
1.3 成像坐标选择
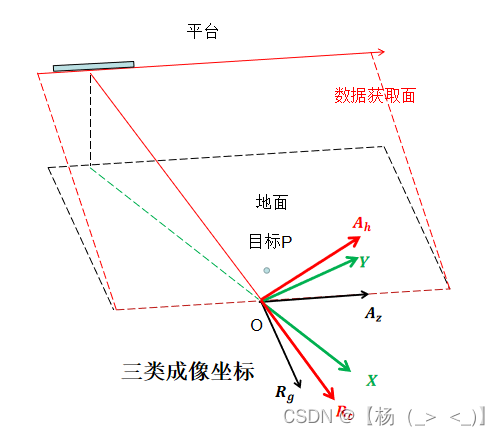
在进行BP成像过程中,进行网格剖分时,有几种坐标系的选择。 如上图所示, SAR成像中有三类常见的成像直角坐标系,以成像场景中心为坐标原点,下面结合上述场景图具体介绍:
-
固定场景直角坐标系
如上图黑色坐标系所示,SAR成像面位于地面,以平行于平台的飞行方向为方位向,垂直于飞行方向且位于地面的方向为地距方向
-
沿视线直角坐标系
如上图绿色坐标系所示,SAR成像面位于地面,以雷达视线沿地面的投影为轴,垂直于
轴且与飞行方向夹角小于90°的方向为
。
-
数据获取面直角坐标系
如上图红色坐标系所示,SAR成像面位于地面,以雷达视线方向为距离向,垂直于距离向,且与飞行方向夹角小于90°的方向为距离横向
。
-
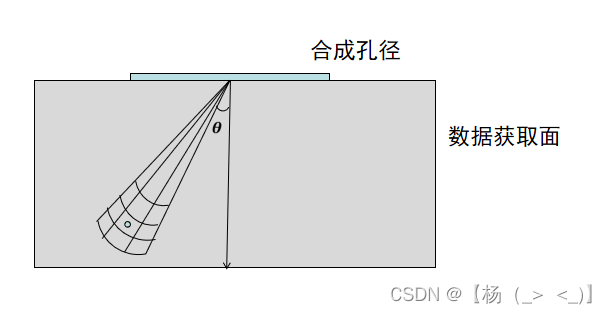
数据获取面极坐标系
如上图所示,以合成孔径中心为原点,垂直于孔径方向为0方位角方向,成像平面位于数据获取面内。
二、 BP算法
不同模式下的BP算法原理:首先在选定的成像坐标系(四类坐标系)下对特定的成像平面进行网格剖分,然后针对不同的网格剖分点,结合成像场景的几何构型,计算对应的距离徙动曲线,最后沿着距离徙动曲线进行相干累加,累加的模值作为SAR图像值。
下面简单介绍成像场景不同因素对BP算法的影响。首先正侧视以及斜视的几何构型对成像算法并不产生影响。其次雷达的工作模式决定了方位向信号的范围,即影响距离徙动曲线方位向范围。最后,在斜视模式下,不同成像平面以及坐标系下,得到的SAR图像为不同视角下的“所见”图像,因此具有不同的特征。下面结合仿真具体介绍:
三、仿真结果
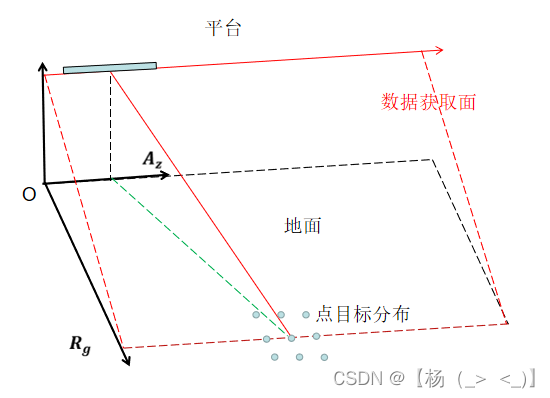
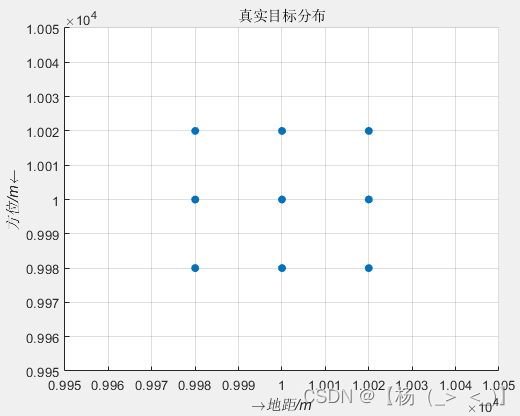
上图分别是SAR成像场景图以及真实点目标分布图。下面具体分析不同坐标系下的BP算法成像结果。
3.1.条带+正侧视+固定场景直角坐标系
坐标系为固定场景坐标系,与第一节介绍的略有不同,场景中心没有甚至为坐标原点,而是将平台某时刻的地面投影位置甚至为原点,此时成像场景中心位置为,距离10km,方位10km,搜索范围100m*100m,搜索间隔0.2m*0.1m。目标为3*3分布的矩形点列,距离方位间距皆为20m,下图为BP算法成像结果:
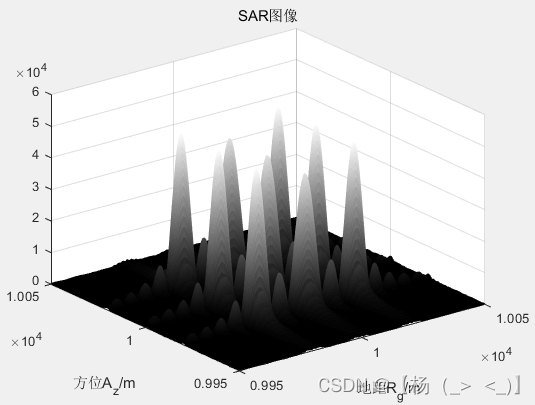
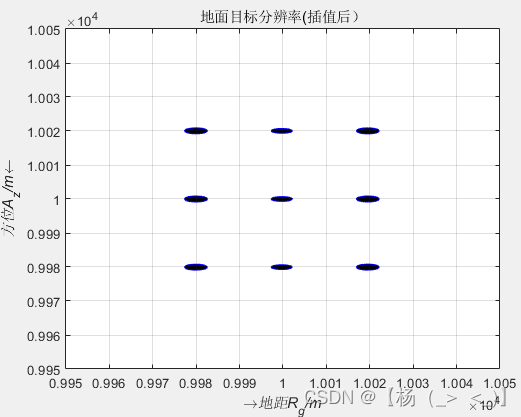
从结果可以看出,该坐标系下的SAR图像与实际布置的目标分布图一致。
3.2 聚束+斜视+固定场景直角坐标系
斜视角为-30°,负号表示前视,下面为BP算法成像结果:
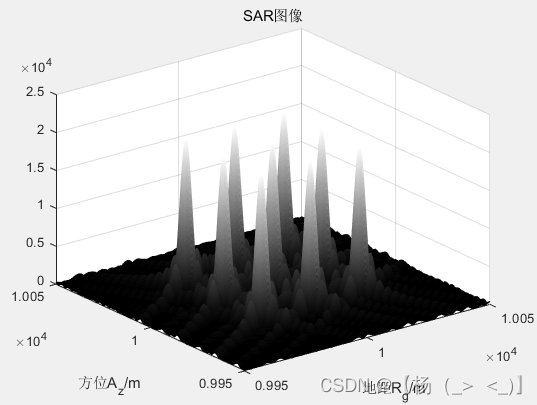
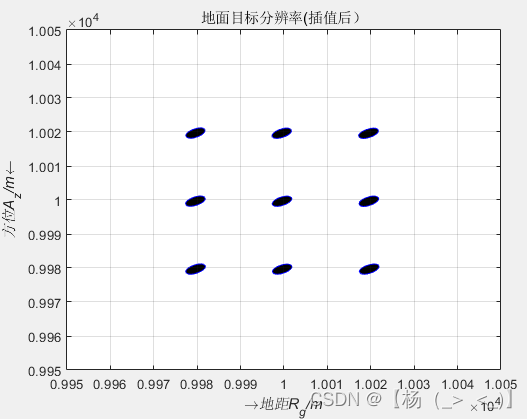
与正视相比,斜视情况该坐标系下所成图像的目标点分布与实际布置的目标分布图一致,只是距离分辨轴向与地距方向发生斜视角度的旋转。
3.3 聚束+斜视+沿视线直角坐标系
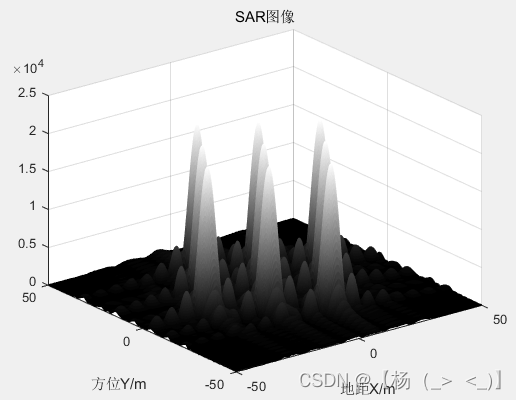
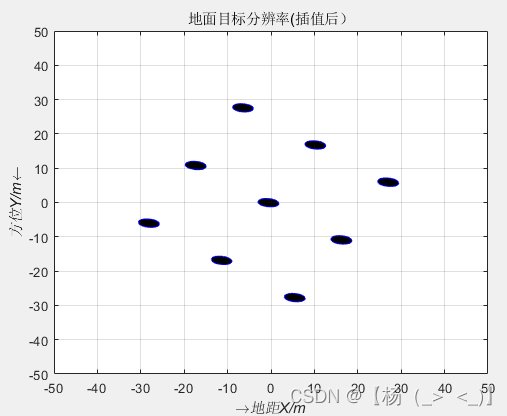
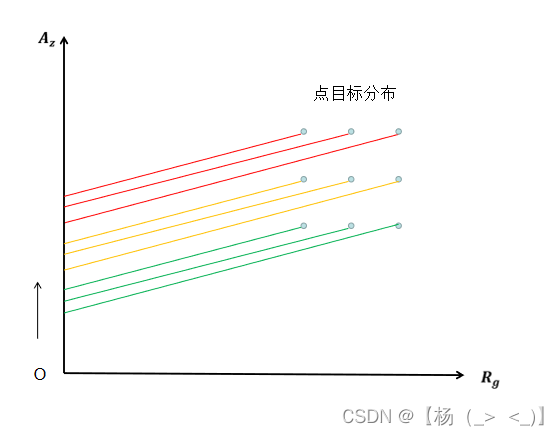
上图是该坐标系下的成像结果,其成像结果可由下图得到解释。以前视为例,当飞行平台移动时,雷达波束中心首先经过最近方位最远地距的目标点,所以针对同方位不同距离的目标,雷达首先探测到最远距离的目标,最后探测到最近距离的目标,这与上述成像结果是相符的。
3.4 聚束+斜视+数据获取面直角坐标系
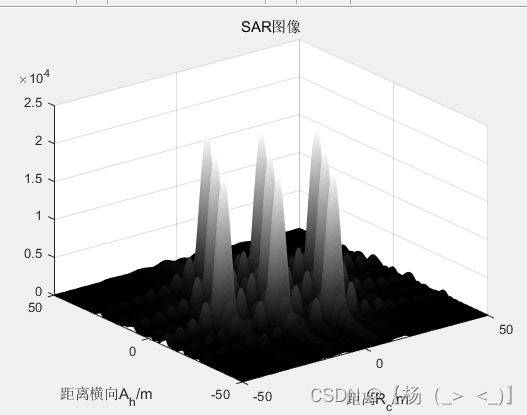
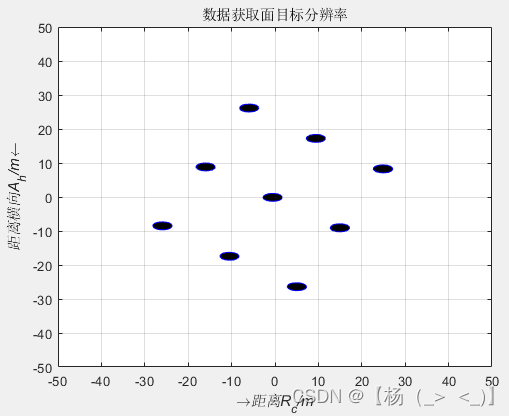
上图是在数据获取面直角坐标系得到成像结果,其形成图像的原因与3.3节的基本一致,这里不再重复。
3.5 聚束+斜视+数据获取面极坐标系
目标方向在参考方向(垂直航向方向)的右侧,方位角为正,因此对应前视情况,目标的方位角为正值,下面为BP算法成像结果:

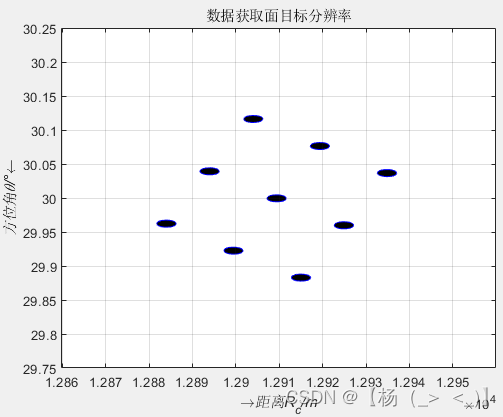
代码:《SAR+BPA算法+根据回波信号生成SAR图像(斜视)》
总结
上述SAR的内容主要依赖自身理解,可能存在一些争议的地方,有任何问题都可以评论区留言。另外觉得博主写的内容不错,希望各位支持一下,你们的反馈真的很重要。
本文主要介绍了不同成像场景下BP算法所成SAR图像特点。结合BP算法,讲述了SAR成像中扫面模式、几何构型以及成像坐标的概念以及对算法的影响。转载请附上链接:【杨(_> <_)】的博客_CSDN博客-信号处理,SAR,代码实现领域博主


![[极客大挑战 2019]Havefun、[ACTF2020 新生赛]Include、[SUCTF 2019]EasySQL](https://img-blog.csdnimg.cn/070d1f4a3cd34343b6856dccaa6c8a7e.png)