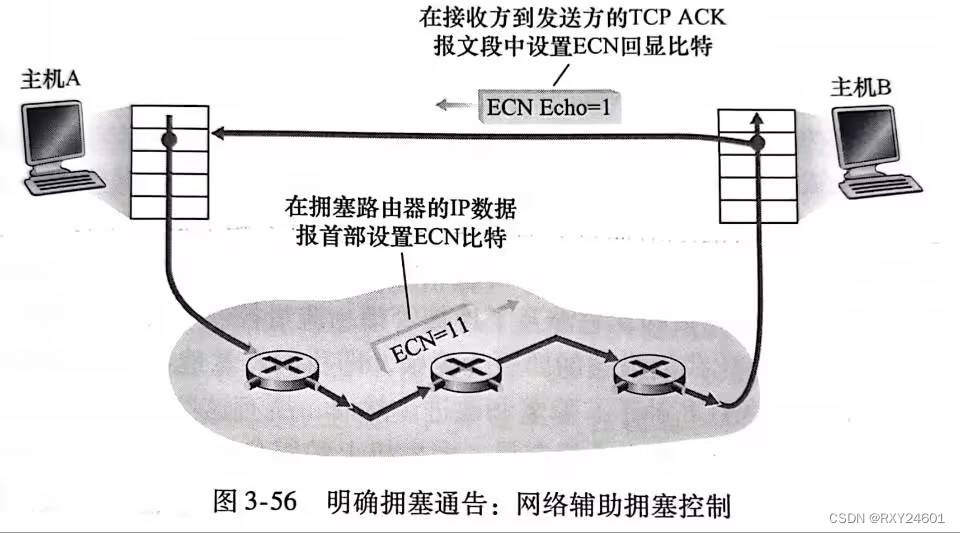
概述

逻辑回归（Logistic Regression）是一种用于解决二分类或多分类问题的统计学习方法。它以自变量线性组合的形式进行建模，并使用Sigmoid函数将结果映射到[0, 1]的值域内，表示样本属于某个类别的概率。
Logistic Regression是最广泛使用的一种算法，逻辑回归常年在机器学习算法排名前10。

逻辑回归推导

线性回归

线性回归的表达式：
$f(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+....+{\theta }_n{x}_n$
转换为矩阵乘法：
$[[x_1,x_2....,x_n]]$点乘$[[{\theta }_1,{\theta }_2.....,{\theta }_n]{]}^T$
矩阵演示：
首先，假设我们有一个包含3个样本、每个样本有2个特征的训练集X：

X = [[1, 2], [3, 4], [5, 6]]

其中，每个样本都有两个特征。接着，我们随机初始化参数向量θ：

θ = [[0.5,0.5]]
θ.T=[[0.5],[0.5]]
X * θ = [[1, 2], [3, 4], [5, 6]] * [[0.5], [0.5]] = [[10.5+20.5], [30.5+40.5], [50.5+60.5]] = [[1.5], [3.5], [5.5]]

所以：
$f(x)={\theta }_0+{\theta }^{T}x$
如果在x数据集加上一列常量1，${\theta }_0$加入到$\theta$矩阵中，也就能再次缩写
$f(x)={\theta }^{T}x$

$\theta$是权值,它与输出y之间的关系强度。如果权值越大，则输入特征对输出的影响就越大；如果权值越小，则输入特征对输出的影响就越小。。

逻辑回归

逻辑回归(Logistic Regression, LR)模型其实仅在线性回归的基础上，套用了一个逻辑函数，但也就由于这个逻辑函数，使得逻辑回归模型成为了机器学习领域一颗耀眼的明星，更是计算广告学的核心。
通常线性方程的值域为 $(-\infty ，+\infty )$,而概率的值域为[0, 1]，因此我们在这个基础上做一个变形，完成从 $(-\infty ，+\infty )$,到[0,1]的转换。
逻辑回归的假设函数可以表示为
$$h_{\theta }(x)=g({\theta }^{T}x)$$
这个转换函数g就叫做Sigmoid函数，函数的表达式：
$$g(z)=\frac{1}{(1+e^{-z})}$$
我们来看下Sigmoid函数的图形

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(t):
    return 1 / (1 + np.exp(-t))

x = np.linspace(-10, 10, 500)
y = sigmoid(x)
plt.plot(x, y)
plt.show()

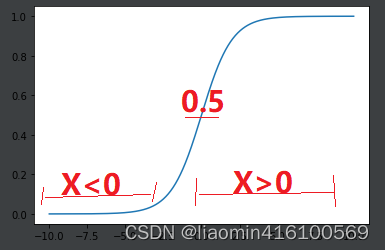
于是我们得到了这样的关系式：

• X（也就是${\theta }^{T}x$）>0时，Y的值（概率）大于0.5，label也就是1
• X<0时，Y的值（概率）小于0.5，label也就是0
• X=0时，Y的值=0.5

二分类问题，比如是否有肿瘤，概率大于0.5预测就是明确的1，概率小于0.5预测就是明确的0

决策边界

下面再举一个例子，假设我们有许多样本，并在图中表示出来了，并且假设我们已经通过某种方法求出了LR模型的参数（如下图）。

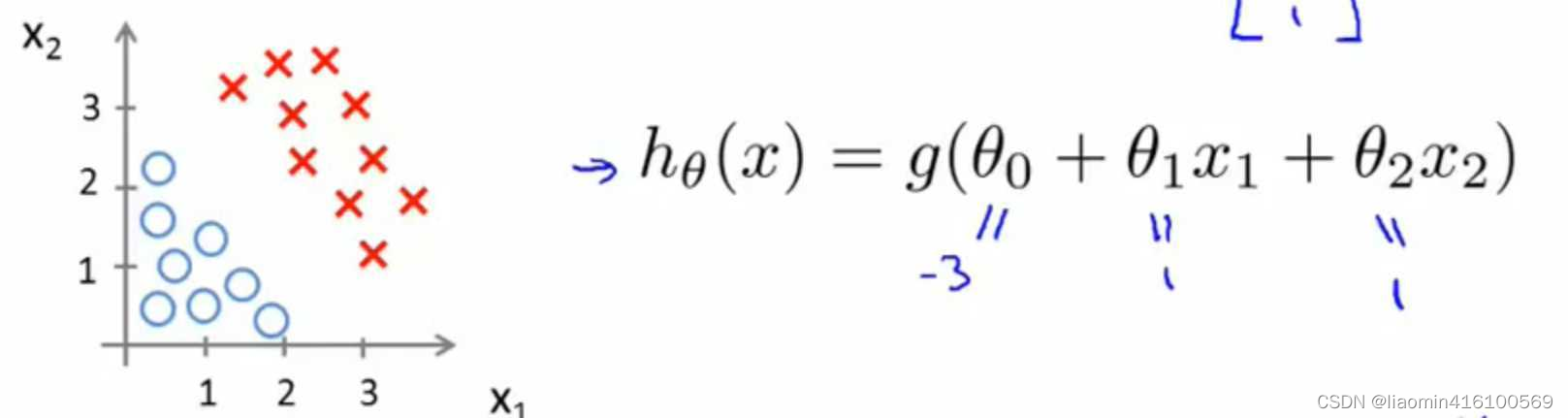
根据上面得到的关系式，我们可以得到：

我们再图像上画出得到：

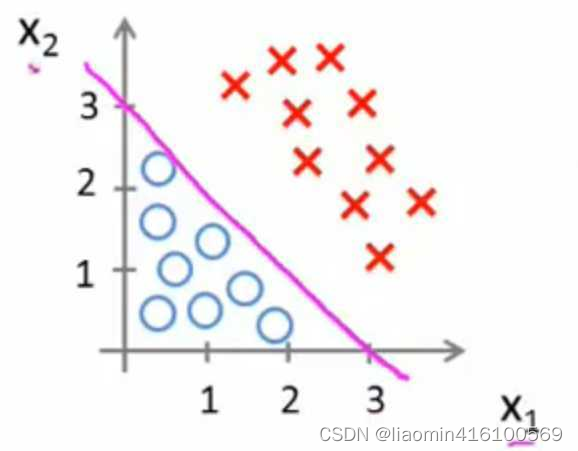
这时，直线上方所有样本都是正样本y=1，直线下方所有样本都是负样本y=0。因此我们可以把这条直线成为**决策边界**。
同理，对于非线性可分的情况，我们只需要引入多项式特征就可以很好的去做分类预测，如下图：

得注意的一点，决策边界并不是训练集的属性，而是假设本身和参数的属性。因为训练集不可以定义决策边界，它只负责拟合参数；而只有参数确定了，决策边界才得以确定。

损失函数

损失函数就是用来衡量模型的输出与真实输出的差别。
假设只有两个标签1和0， y n ∈ { 0 , 1 } y_n\in\{0,1\} yn​∈{0,1} 。我们把采集到的任何一组样本看做一个事件的话，那么这个事件发生的概率假设为p。我们的模型y的值等于标签为1的概率也就是p。

交叉熵（Cross-Entropy，CE）和均方误差（Mean Squared Error，MSE）是机器学习中经常使用的两种损失函数。它们在许多领域都被广泛应用，例如分类、回归等任务。它们的区别在于对于不同类型的问题，理论依据和优化效果不同。

• MSE通常用于回归问题，用于衡量预测值与真实值之间的差异
• 而CE则通常用于分类问题中，它可以衡量预测结果与真实标签之间的差异。对于二分类问题，它的公式为：

MSE(均方误差)

为什么损失函数不用最小二乘？即逻辑斯蒂回归损失函数为什么使用交叉熵（下一节）而不是MSE？
从逻辑的角度出发，我们知道逻辑斯蒂回归的预测值是一个概率，而交叉熵又表示真实概率分布与预- 测概率分布的相似程度，因此选择使用交叉熵。
从MSE的角度来说，预测的概率与欧氏距离没有任何关系，并且在分类问题中，样本的值不存在大小关系，与欧氏距离更无关系，因此不适用MSE。

原因一：损失函数的凸性（使用MSE可能会陷入局部最优）
前面我们介绍线性回归模型时，给出了线性回归的代价函数的形式（误差平方和函数），具体形式如下：
$$J(\theta )=\frac{1}{m}\sum _{i=1}^m\frac{1}{2}(h_{\theta }(x^{(j)})-y^{(j)})$$
这里我们想到逻辑回归也可以视为一个广义的线性模型，那么线性模型中应用最广泛的代价函数-误差平方和函数，可不可以应用到逻辑回归呢？首先告诉你答案：是不可以的！ 那么为什么呢? 这是因为LR的假设函数的外层函数是Sigmoid函数，Sigmoid函数是一个复杂的非线性函数，这就使得我们将逻辑回归的假设函数
$$h_{\theta }(x)=\frac{1}{(1+e^{-{\theta }^{T}x})}$$
带入上式时，我们得到的
$$J(\theta )=\frac{1}{m}\sum _{i=1}^m\frac{1}{2}(\frac{1}{(1+e^{-{\theta }^T{x}^{(j)}})}-y^{(j)})$$

是一个非凸函数，如下图：

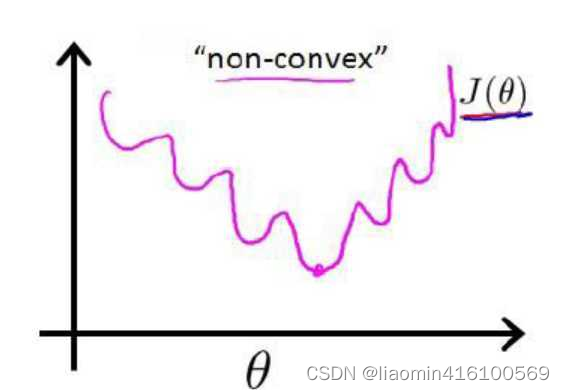
这样的函数拥有多个局部极小值，这就会使得我们在使用梯度下降法求解函数最小值时，所得到的结果并非总是全局最小，而有更大的可能得到的是局部最小值

MSE 为损失函数的逻辑斯蒂回归就是一个非凸函数，如何证明这一点呢，要证明一个函数的凸性，只要证明其二阶导恒大于等于0即可，如果不是恒大于等于0，则为非凸函数。

• 凸（Convex）：在该区间函数图象上的任意两点所连成的线段上的每一个点都位于函数图象的下方(或上方)。
  一个典型的凸函数$y=-x^2$
  ，任意两点连线上所有的点都在函数图像的下方，如下图：
  

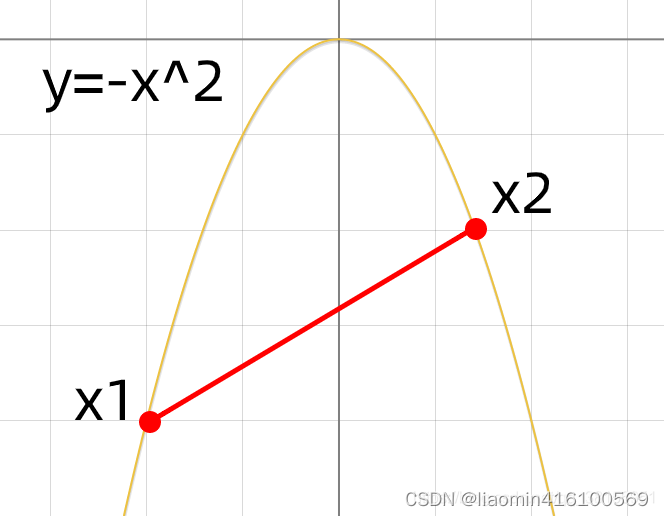
• 非凸（Non-Convex）：函数在该区间上有多个极值,即系统有多个稳定的平衡态。
  非凸函数$y=sin(x)$，两点连线上的点可能分布在函数图像的两侧，如下图：
  
  这里只需要证明上面函数不是恒大于等于0即可，这里就不去证明了，自行百度。

CE（交叉熵）

逻辑回归损失函数就是用来衡量模型的输出与真实输出的差别。
假设只有两个标签1和0， y n ∈ { 0 , 1 } y_n \in\{0, 1\} yn​∈{0,1}。我们把采集到的任何一组样本看做一个事件的话，那么这个事件发生的概率假设为p。我们的模型y的值等于标签为1的概率也就是p。
$$P_{y=1}=\frac{1}{1+e^{-{\mathbf{\theta }}^T\mathbf{x}}}=p$$
因为标签不是1就是0，因此标签为0的概率就是：$P_{y=0}=1-p$
我们把单个样本看做一个事件，那么这个事件发生的概率就是：
$$P(y|\mathbf{x})=\{\begin{array}{r}p,y=1\\ 1-p,y=0\end{array}$$
这个函数不方便计算，它等价于:
$$P(y_i|{\mathbf{x}}_i)=p^{y_i}(1-p{)}^{1-y_i}$$
解释下这个函数的含义，我们采集到了一个样本$({\mathbf{x}}_{\mathbf{i}},y_i)$对这个样本，它的标签是$y_i$的概率是
$p^{y_i}(1-p{)}^{1-y_i}$ （当y=1，结果是p；当y=0，结果是1-p）。
如果我们采集到了一组数据一共N个，$\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),({\mathbf{x}}_3,y_3)...({\mathbf{x}}_N,y_N)\}$，这个合成在一起的合事件发生的总概率怎么求呢？其实就是将每一个样本发生的概率相乘就可以了，即采集到这组样本的概率：
$$\begin{array}{rl}{P}_{总}& =P(y_1|{\mathbf{x}}_1)P(y_2|{\mathbf{x}}_2)P(y_3|{\mathbf{x}}_3)....P(y_N|{\mathbf{x}}_N)\\ & =\prod _{n=1}^N{p}^{y_n}(1-p{)}^{1-y_n}\end{array}$$

注意$P_{总}$ 是一个函数，并且未知的量只有 $\theta$ （在p里面）。
由于连乘很复杂，我们通过两边取对数来把连乘变成连加的形式,对数可以防止下溢出，不会影响单调性，同时和原函数在相同的点求极限值，也就是找到的是相同$\theta$值，即：
$$\begin{array}{rl}F(\mathbf{\theta })=ln(P_{总})& =ln(\prod _{n=1}^N{p}^{y_n}(1-p{)}^{1-y_n})\\ & =\sum _{n=1}^{N}ln(p^{y_n}(1-p{)}^{1-y_n})\\ & =\sum _{n=1}^N(y_{n}ln(p)+(1-y_n)ln(1-p))\end{array}$$

其中，$p=\frac{1}{1+e^{-{\mathbf{\theta }}^T\mathbf{x}}}$
这个函数$F(\mathbf{w})$的值等于事件发生的总概率，我们希望它越大越好。但是跟损失的含义有点儿违背，因此也可以在前面取个负号，负数就是越小越好，$-F(\mathbf{w})$又叫做它的损失函数。损失函数可以理解成衡量我们当前的模型的输出结果，跟实际的输出结果之间的差距的一种函数。
损失函数也就是交叉熵

$$\begin{array}{r}J(\mathbf{\theta })=-ln(P_{总})=-\sum _{n=1}^N(y_{n}ln(p)+(1-y_n)ln(1-p))\end{array}$$

在逻辑回归中，我们通常使用交叉熵作为损失函数来评估模型预测结果和实际标签之间的差异。损失函数的目标是尽可能地缩小模型的预测误差，使模型能够更准确地预测数据的标签。

在实际训练中，我们通常会将整个训练集分为若干个小批次（batch），利用每个小批次的数据对模型参数进行更新。这样做的好处是可以提高模型训练的速度，减少模型在训练过程中的波动性。

为了避免样本数量对损失函数大小的影响，通常在计算损失函数时会将所有样本损失函数值的平均作为最终的损失函数值。也就是说，用上面的公式计算出来的是训练集中所有样本的平均损失函数。
$$\begin{array}{r}J(\mathbf{\theta })=-\frac{1}{n}\sum _{n=1}^N(y_{n}ln(p)+(1-y_n)ln(1-p))\end{array}$$
而除以样本数量m，其实就是将平均损失函数转化为单个样本的损失函数，即用每个样本的损失函数值的平均值来衡量模型在单个样本上的错误程度。这样做可以使优化算法更加稳定和可靠。
好的，假设我们的训练集中有1000个样本，我们将其分成10个小批次（每个小批次包含100个样本）进行训练。模型对每个小批次的样本进行预测

那么，使用如下的公式计算这个模型的交叉熵损失：

$$\text{CE}(\mathbf{y},\hat{\mathbf{y}})=J(\mathbf{\theta })=-\frac{1}{10\times 100}\sum _{i=1}^{10\times 100}[y_i{\log }_e{\hat{y}}_i+(1-y_i){\log }_e(1-{\hat{y}}_i)]$$

1000个样本的平均损失函数值。在实际训练中，优化算法通常是按照小批次的形式进行迭代更新的，因此使用平均损失函数可以对单个小批次的数据完整反映模型对整个训练集数据的学习程度。

而如果我们不将损失函数除以样本数量m，那么不同样本数量的训练集会对损失函数大小产生影响，从而使得优化算法在训练时产生不必要的波动和不稳定。

CE梯度推导

我们指导入到需要使用梯度下降法求出最小值的$\theta$，需要先获取到损失函数的梯度。
首先，我们需要知道向量是如何求导的。具体的推导过程以及原理请参见梯度下降

首先我们知道
$$p=\frac{1}{1+e^{-{\mathbf{\theta }}^T\mathbf{x}}}$$
那么
$$1-p=1-\frac{1}{1+e^{-{\mathbf{\theta }}^T\mathbf{x}}}=\frac{1+e^{-{\mathbf{\theta }}^T\mathbf{x}}}{1+e^{-{\mathbf{\theta }}^T\mathbf{x}}}-\frac{1}{1+e^{-{\mathbf{\theta }}^T\mathbf{x}}}=\frac{e^{-{\mathbf{\theta }}^T\mathbf{x}}}{1+e^{-{\mathbf{\theta }}^T\mathbf{x}}}$$
p是一个关于变量 $\theta$ 的函数，我们对p求导，通过链式求导法则，慢慢展开可以得：
$\begin{array}{rl}{p}^{\prime }=f^{\prime }(\mathbf{\theta })& =(\frac{1}{1+e^{-{\mathbf{\theta }}^T\mathbf{x}}}{)}^{\prime }\\ & =-\frac{1}{(1+e^{-{\mathbf{\theta }}^T\mathbf{x}}{)}^2}\cdot (1+e^{-{\mathbf{\theta }}^T\mathbf{x}}{)}^{\prime }\\ & =-\frac{1}{(1+e^{-{\mathbf{\theta }}^T\mathbf{x}}{)}^2}\cdot e^{-{\mathbf{\theta }}^T\mathbf{x}}\cdot (-{\mathbf{\theta }}^T\mathbf{x}{)}^{\prime }\\ & =-\frac{1}{(1+e^{-{\mathbf{\theta }}^T\mathbf{x}}{)}^2}\cdot e^{-{\mathbf{\theta }}^T\mathbf{x}}\cdot (-\mathbf{x})\\ & =\frac{e^{-{\mathbf{\theta }}^T\mathbf{x}}}{(1+e^{-{\mathbf{\theta }}^T\mathbf{x}}{)}^2}\cdot \mathbf{x}\\ & =\frac{1}{1+e^{-{\mathbf{\theta }}^T\mathbf{x}}}\cdot \frac{e^{-{\mathbf{\theta }}^T\mathbf{x}}}{1+e^{-{\mathbf{\theta }}^T\mathbf{x}}}\cdot \mathbf{x}\\ & =p(1-p)\mathbf{x}\end{array}$

上面都是我们做的准备工作，总之我们得记住：
$p^{\prime }=p(1-p)\mathbf{x}$
那么
$(1-p{)}^{\prime }=1^{\prime }-p^{\prime }=-p^{\prime }=-p(1-p)\mathbf{x}$
接下来我们对$J_{\theta }求导$，求导的时候请始终记住，我们的变量只有 $\theta$，其他的什么
都是已知的，可以看做常数。
$\begin{array}{rl}\nabla J（\mathbf{\theta }）& =\nabla （\sum _{n=1}^N(y_{n}ln(p)+(1-y_n)ln(1-p))）\\ & =\sum (y_{n}l{n}^{\prime }(p)+(1-y_n)l{n}^{\prime }(1-p))\\ & =\sum ((y_n\frac{1}{p}{p}^{\prime })+(1-y_n)\frac{1}{1-p}(1-p{)}^{\prime })\\ & =\sum (y_n(1-p){\mathbf{x}}_n-(1-y_n)p{\mathbf{x}}_n)\\ & =\sum _{n=1}^N(y_n-p){\mathbf{x}}_n\end{array}$

终于，我们求出了梯度$J（\mathbf{\theta }）$的表达式了，现在我们再来看看它长什么样子：
$\begin{array}{rl}\nabla J（\mathbf{\theta }）& =\sum _{n=1}^N(y_n-p){\mathbf{x}}_n\end{array}$
它是如此简洁优雅，这就是我们选取sigmoid函数的原因之一。当然我们也能够把p再展开，即：

$\begin{array}{rl}\nabla J（\mathbf{\theta }）& =\sum _{n=1}^N(y_n-\frac{1}{1+e^{-{\mathbf{\theta }}^T{\mathbf{x}}_n}}){\mathbf{x}}_n\end{array}$

梯度下降法（GD）与随机梯度下降法（SGD）

现在我们已经解出了损失函数 $J_{\theta }$在任意 $\theta$处的梯度 $\nabla J（\mathbf{\theta }）$，可是我们怎么算出来 $\theta \ast$ 呢？ 回到之前的问题，我们现在要求损失函数取最小值时候的的$\theta \ast$值：
${\mathbf{\theta }}^{\ast }=arg{\min }_{w}J(\mathbf{\theta })$，

梯度下降法(Gradient Descent)，可以用来解决这个问题。核心思想就是先随便初始化一个${\theta }_0$
然后给定一个步长$\eta$ 通过不断地修改$\mathbf{\theta }$，从而最后靠近到达取得最小值的点，即不断进行下面的迭代过程，直到达到指定次数，或者梯度等于0为止。
${\mathbf{\theta }}_{t+1}={\mathbf{\theta }}_t+\eta \nabla F（\mathbf{\theta }）$

随机梯度下降法（Stochastic Gradient Descent），如果我们能够在每次更新过程中，加入一点点噪声扰动，可能会更加快速地逼近最优值。在SGD中，我们不直接使用$\nabla F（\mathbf{\theta }）$,，而是采用另一个输出为随机变量的替代函数 $G(\mathbf{\theta })$
${\mathbf{\theta }}_{t+1}={\mathbf{\theta }}_t+\eta G(\mathbf{\theta })$
当然，这个替代函数 $G(\mathbf{\theta })$需要满足它的期望值等于$\nabla F（\mathbf{\theta }）$，相当于这个函数围绕着$\nabla F（\mathbf{\theta }）$的输出值随机波动。

在这里我先解释一个问题：为什么可以用梯度下降法？

因为逻辑回归的损失函数L是一个连续的凸函数（conveniently convex）。这样的函数的特征是，它只会有一个全局最优的点，不存在局部最优。对于GD跟SGD最大的潜在问题就是它们可能会陷入局部最优。然而这个问题在逻辑回归里面就不存在了，因为它的损失函数的良好特性，导致它并不会有好几个局部最优。当我们的GD跟SGD收敛以后，我们得到的极值点一定就是全局最优的点，因此我们可以放心地用GD跟SGD来求解。

好了，那我们要怎么实现学习算法呢？其实很简单，注意我们GD求导每次都耿直地用到了所有的样本点，从1一直到N都参与梯度计算。
$\begin{array}{rl}\nabla J（\mathbf{\theta }）& =-\sum _{n=1}^N(y_n-\frac{1}{1+e^{-{\mathbf{\theta }}^T{\mathbf{x}}_n}}){\mathbf{x}}_n\end{array}$
在SGD中，我们每次只要均匀地、随机选取其中一个样本 $({\mathbf{x}}_{\mathbf{i}},y_i)$,用它代表整体样本，即把它的值乘以N，就相当于获得了梯度的无偏估计值，即 $E(G(\mathbf{\theta }))=\nabla F(\mathbf{\theta })$

E代表期望值，通常表示为E(X)，其中X是一个随机变量，表示对这个随机变量的所有可能取值按概率加权的平均值。

这样我们前面的求和就没有了，同时$\eta N$都是常数,N的值刚好可以并入$\eta$中，因此SGD的迭代更新公式为：
${\mathbf{\theta }}_{t+1}={\mathbf{\theta }}_t+\eta (y_n-\frac{1}{1+e^{-{\mathbf{\theta }}^T{\mathbf{x}}_n}}){\mathbf{x}}_n$
其中$({\mathbf{x}}_{\mathbf{i}},y_i)$是对所有样本随机抽样的一个结果。

可解释性

辑回归最大的特点就是可解释性很强。
在模型训练完成之后，我们获得了一组n维的权重向量$\theta \ast$和偏差${\theta }_0$
对于权重向量$\theta \ast$，它的每一个维度的值，代表了这个维度的特征对于最终分类结果的贡献大小。假如这个维度是正，说明这个特征对于结果是有正向的贡献，那么它的值越大，说明这个特征对于分类为正起到的作用越重要。

对于偏差${\theta }_0$，一定程度代表了正负两个类别的判定的容易程度。假如${\theta }_0$是0，那么正负类别是均匀的。如果${\theta }_0$大于0，说明它更容易被分为正类，反之亦然。

根据逻辑回归里的权重向量在每个特征上面的大小，就能够对于每个特征的重要程度有一个量化的清楚的认识，这就是为什么说逻辑回归模型有着很强的解释性的原因。

正则项

对于线性回归模型，使用L1正则化的模型建叫做Lasso回归，使用L2正则化的模型叫做Ridge回归（岭回归）为了解决过拟合问题，具体参考:https://blog.csdn.net/liaomin416100569/article/details/130289602?spm=1001.2014.3001.5501。

如何用逻辑回归处理多标签问题

逻辑斯蒂回归本身只能用于二分类问题，如果实际情况是多分类的，那么就需要对模型进行一些改动，以下是三种比较常用的将逻辑斯蒂回归用于多分类的方法：

One vs One

OvO 的方法就是将多个类别中抽出来两个类别，然后将对应的样本输入到一个逻辑斯蒂回归的模型中，学到一个对这两个类别的分类器，然后重复以上的步骤，直到所有类别两两之间都存在一个分类器。
假设存在四个类别，那么分类器的数量为6个，表格如下：

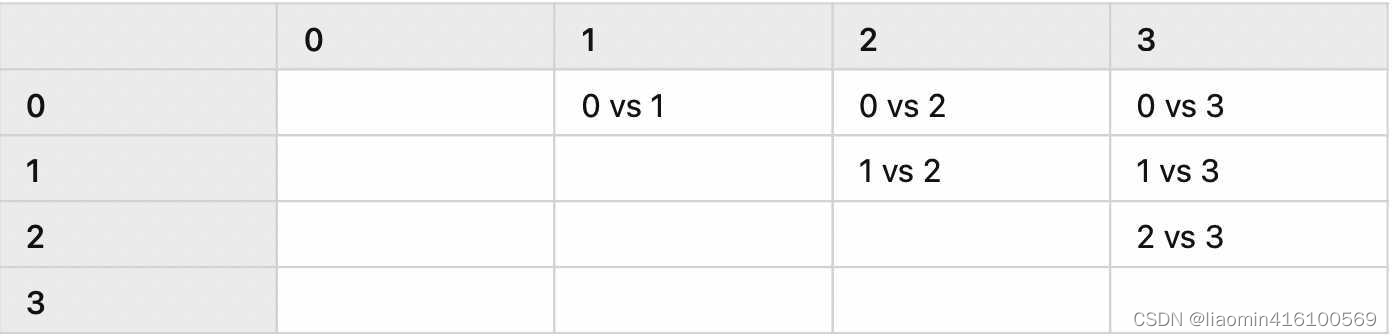
分类器的数量直接使用 $C_2^k$就可以了，k 代表类别的数量。

在预测时，需要运行每一个模型，然后记录每个分类器的预测结果，也就是每个分类器都进行一次投票，取获得票数最多的那个类别就是最终的多分类的结果。

比如在以上的例子中，6个分类器有3个投票给了类别3，1个投票给了类别2，1个投票给类别1，最后一个投票给类别0，那么就取类别3为最终预测结果。

OvO 的方法中，当需要预测的类别变得很多的时候，那么我们需要进行训练的分类器也变得很多了，这一方面提高了训练开销，但在另一方面，每一个训练器中，因为只需要输入两个类别对应的训练样本即可，这样就又减少了开销。

从预测的角度考虑，这种方式需要运行的分类器非常多，而无法降低每个分类器的预测时间复杂度，因此预测的开销较大。

One vs All

针对问题：一个样本对应多个标签。
OvA 的方法就是从所有类别中依次选择一个类别作为1，其他所有类别作为0，来训练分类器，因此分类器的数量要比 OvO 的数量少得多。

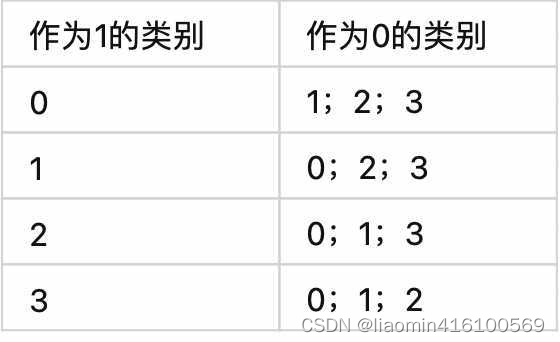
通过以上例子可以看到，分类器的数量实际上就是类别的数量，也就是k。

虽然分类器的数量下降了，但是对于每一个分类器来说，训练时需要将所有的训练数据全部输入进去进行训练，因此每一个分类器的训练时间复杂度是高于 OvO 的。

从预测的方面来说，因为分类器的数量较少，而每个分类器的预测时间复杂度不变，因此总体的预测时间复杂度小于 OvA。

预测结果的确定，是根据每个分类器对其对应的类别1的概率进行排序，选择概率最高的那个类别作为最终的预测类别。

sklearn实战

LogisticRegression训练乳腺癌肿瘤分类

klearn.linear_model模块提供了很多模型供我们使用，比如Logistic回归、Lasso回归、贝叶斯脊回归等，可见需要学习的东西还有很多很多。我们使用LogisticRegressioin。
让我们先看下LogisticRegression这个函数，一共有14个参数：

参数说明如下：

• penalty：惩罚项，str类型，可选参数为l1和l2，默认为l2。用于指定惩罚项中使用的规范。newton-cg、sag和lbfgs求解算法只支持L2规范。L1G规范假设的是模型的参数满足拉普拉斯分布，L2假设的模型参数满足高斯分布，所谓的范式就是加上对参数的约束，使得模型更不会过拟合(overfit)，但是如果要说是不是加了约束就会好，这个没有人能回答，只能说，加约束的情况下，理论上应该可以获得泛化能力更强的结果。
• dual：对偶或原始方法，bool类型，默认为False。对偶方法只用在求解线性多核(liblinear)的L2惩罚项上。当样本数量>样本特征的时候，dual通常设置为False。
• tol：停止求解的标准，float类型，默认为1e-4。就是求解到多少的时候，停止，认为已经求出最优解。
• c：正则化系数λ的倒数，float类型，默认为1.0。必须是正浮点型数。像SVM一样，越小的数值表示越强的正则化。
• fit_intercept：是否存在截距或偏差，bool类型，默认为True。
• intercept_scaling：仅在正则化项为"liblinear"，且fit_intercept设置为True时有用。float类型，默认为1。
• class_weight：用于标示分类模型中各种类型的权重，可以是一个字典或者’balanced’字符串，默认为不输入，也就是不考虑权重，即为None。如果选择输入的话，可以选择balanced让类库自己计算类型权重，或者自己输入各个类型的权重。举个例子，比如对于0,1的二元模型，我们可以定义class_weight={0:0.9,1:0.1}，这样类型0的权重为90%，而类型1的权重为10%。如果class_weight选择balanced，那么类库会根据训练样本量来计算权重。某种类型样本量越多，则权重越低，样本量越少，则权重越高。当class_weight为balanced时，类权重计算方法如下：n_samples / (n_classes * np.bincount(y))。n_samples为样本数，n_classes为类别数量，np.bincount(y)会输出每个类的样本数，例如y=[1,0,0,1,1],则np.bincount(y)=[2,3]。
  那么class_weight有什么作用呢？
  在分类模型中，我们经常会遇到两类问题：
  1.第一种是误分类的代价很高。比如对合法用户和非法用户进行分类，将非法用户分类为合法用户的代价很高，我们宁愿将合法用户分类为非法用户，这时可以人工再甄别，但是却不愿将非法用户分类为合法用户。这时，我们可以适当提高非法用户的权重。

2. 第二种是样本是高度失衡的，比如我们有合法用户和非法用户的二元样本数据10000条，里面合法用户有9995条，非法用户只有5条，如果我们不考虑权重，则我们可以将所有的测试集都预测为合法用户，这样预测准确率理论上有99.95%，但是却没有任何意义。这时，我们可以选择balanced，让类库自动提高非法用户样本的权重。提高了某种分类的权重，相比不考虑权重，会有更多的样本分类划分到高权重的类别，从而可以解决上面两类问题。

• random_state：随机数种子，int类型，可选参数，默认为无，仅在正则化优化算法为sag,liblinear时有用。
• solver：优化算法选择参数，只有五个可选参数，即newton-cg,lbfgs,liblinear,sag,saga。默认为liblinear。solver参数决定了我们对逻辑回归损失函数的优化方法，有四种算法可以选择，分别是：
  liblinear：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。
  lbfgs：拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
  newton-cg：也是牛顿法家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
  sag：即随机平均梯度下降，是梯度下降法的变种，和普通梯度下降法的区别是每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。
  saga：线性收敛的随机优化算法的的变重。
  总结：
  liblinear适用于小数据集，而sag和saga适用于大数据集因为速度更快。
  对于多分类问题，只有newton-cg,sag,saga和lbfgs能够处理多项损失，而liblinear受限于一对剩余(OvR)。啥意思，就是用liblinear的时候，如果是多分类问题，得先把一种类别作为一个类别，剩余的所有类别作为另外一个类别。一次类推，遍历所有类别，进行分类。
  newton-cg,sag和lbfgs这三种优化算法时都需要损失函数的一阶或者二阶连续导数，因此不能用于没有连续导数的L1正则化，只能用于L2正则化。而liblinear和saga通吃L1正则化和L2正则化。
  同时，sag每次仅仅使用了部分样本进行梯度迭代，所以当样本量少的时候不要选择它，而如果样本量非常大，比如大于10万，sag是第一选择。但是sag不能用于L1正则化，所以当你有大量的样本，又需要L1正则化的话就要自己做取舍了。要么通过对样本采样来降低样本量，要么回到L2正则化。
  从上面的描述，大家可能觉得，既然newton-cg, lbfgs和sag这么多限制，如果不是大样本，我们选择liblinear不就行了嘛！错，因为liblinear也有自己的弱点！我们知道，逻辑回归有二元逻辑回归和多元逻辑回归。对于多元逻辑回归常见的有one-vs-rest(OvR)和many-vs-many(MvM)两种。而MvM一般比OvR分类相对准确一些。郁闷的是liblinear只支持OvR，不支持MvM，这样如果我们需要相对精确的多元逻辑回归时，就不能选择liblinear了。也意味着如果我们需要相对精确的多元逻辑回归不能使用L1正则化了。
• max_iter：算法收敛最大迭代次数，int类型，默认为10。仅在正则化优化算法为newton-cg, sag和lbfgs才有用，算法收敛的最大迭代次数。
• multi_class：分类方式选择参数，str类型，可选参数为ovr和multinomial，默认为ovr。ovr即前面提到的one-vs-rest(OvR)，而multinomial即前面提到的many-vs-many(MvM)。如果是二元逻辑回归，ovr和multinomial并没有任何区别，区别主要在多元逻辑回归上。
  OvR和MvM有什么不同？
  OvR的思想很简单，无论你是多少元逻辑回归，我们都可以看做二元逻辑回归。具体做法是，对于第K类的分类决策，我们把所有第K类的样本作为正例，除了第K类样本以外的所有样本都作为负例，然后在上面做二元逻辑回归，得到第K类的分类模型。其他类的分类模型获得以此类推。
  而MvM则相对复杂，这里举MvM的特例one-vs-one(OvO)作讲解。如果模型有T类，我们每次在所有的T类样本里面选择两类样本出来，不妨记为T1类和T2类，把所有的输出为T1和T2的样本放在一起，把T1作为正例，T2作为负例，进行二元逻辑回归，得到模型参数。我们一共需要T(T-1)/2次分类。
  可以看出OvR相对简单，但分类效果相对略差（这里指大多数样本分布情况，某些样本分布下OvR可能更好）。而MvM分类相对精确，但是分类速度没有OvR快。如果选择了ovr，则4种损失函数的优化方法liblinear，newton-cg,lbfgs和sag都可以选择。但是如果选择了multinomial,则只能选择newton-cg, lbfgs和sag了。
• verbose：日志冗长度，int类型。默认为0。就是不输出训练过程，1的时候偶尔输出结果，大于1，对于每个子模型都输出。
• warm_start：热启动参数，bool类型。默认为False。如果为True，则下一次训练是以追加树的形式进行（重新使用上一次的调用作为初始化）。
• n_jobs：并行数。int类型，默认为1。1的时候，用CPU的一个内核运行程序，2的时候，用CPU的2个内核运行程序。为-1的时候，用所有CPU的内核运行程序。

二分类使用乳腺癌肿瘤的临床测量指标来演示逻辑回归

load_breast_cancer：乳腺癌数据集，共有569个样本，其中212个恶性、357个良性。
label中1表示恶性，0表示良性

#%%
"""
sklearn中的load_breast_cancer数据集是一个二分类的数据集，包含了乳腺癌肿瘤的临床测量指标
"""
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
data = load_breast_cancer()
# 加载数据集
data = load_breast_cancer()
X = data.data    # 特征
y = data.target  # 标签

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 定义逻辑回归模型
"""
逻辑回归是一种广泛使用的二分类模型，其常用的优化算法是迭代算法，
比如梯度下降算法。收敛是指在训练过程中，模型参数的更新已经收敛到某个稳定的值，
此时继续迭代将不会产生更好的训练效果。max_iter是scikit-learn中LogisticRegression类的一个参数，
表示最大迭代次数，一旦达到这个迭代次数，则认为模型已经收敛。
"""
lr_model = LogisticRegression(max_iter=2100)

# 拟合模型
lr_model.fit(X_train, y_train)

# 预测训练集和测试集上的结果
train_pred = lr_model.predict(X_train)
test_pred = lr_model.predict(X_test)

# 输出准确率
print('Train accuracy score:', accuracy_score(y_train, train_pred))
print('Test accuracy score:', accuracy_score(y_test, test_pred))  # 输出数据集中标签的维度

输出
Train accuracy score: 0.9538461538461539
Test accuracy score: 0.956140350877193

注意逻辑回归配置：max_iter=5000，代表收敛次数，默认100回抛出STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.，如果收敛次数不够可能导致梯度下降无法到达最小的位置。
如果使用默认的100，算出的准确率是0.94，设置为2100,准确率是0.95,设置为2100以上也是0.95时间就很慢，所以2100是个合适的值

补充知识
accuracy_score和mean_squared_error都是用于评估模型性能的指标，但是适用于不同类型的问题。
accuracy_score通常用于分类问题中，它可以衡量分类器在数据集上的分类准确率，其计算公式如下：
$$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$$
其中:

• TP表示真正例（True Positive），即真实为正类且被分类器预测为正类的样本数；
• TN表示真负例（True Negative），即真实为负类且被分类器预测为负类的样本数；
• FP表示假正例（False Positive），即真实为负类但被分类器预测为正类的样本数；
• FN表示假负例（False Negative），即真实为正类但被分类器预测为负类的样本数。

而mean_squared_error则通常用于回归问题中，它可以衡量预测值与真实值之间的差距，其计算公式如下：
$$MSE=\frac{1}{n}\sum _{i=1}^n(y_i-\widehat{y_i}{)}^2$$

总的来说，accuracy_score和mean_squared_error都是用于评估模型性能而且是分类和回归模型的两种标准指标，但是适用于不同类型的问题，accuracy_score适用于分类任务的评估，而mean_squared_error适用于回归任务的评估。

OneVsOneClassifier葡萄酒数据集

OVR分类葡萄酒数据
load_wine数据集是一个经典、易于理解的、多类别分类数据集，一共包含了178个葡萄酒样本，每个样本有13个特征，分为三个类别。这三个类别分别代表了三种不同的葡萄酒品种。具体而言，这三个类别分别为：

• class_0: 代表第一种葡萄酒品种。
• class_1: 代表第二种葡萄酒品种。
• class_2: 代表第三种葡萄酒品种。

代码

#%%

"""
sklearn中的load_breast_cancer数据集是一个二分类的数据集，包含了乳腺癌肿瘤的临床测量指标
"""
from sklearn.datasets import load_wine
from sklearn.linear_model import LogisticRegression
from sklearn.multiclass import OneVsRestClassifier,OneVsOneClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
data = load_wine()
X = data.data    # 特征
y = data.target  # 标签
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 定义逻辑回归模型
lr_model = LogisticRegression(max_iter=2100)
ovr = OneVsRestClassifier(lr_model)
# 拟合模型
ovr.fit(X_train, y_train)

# 预测训练集和测试集上的结果
train_pred = ovr.predict(X_train)
test_pred = ovr.predict(X_test)

# 输出准确率
print('Train accuracy score:', accuracy_score(y_train, train_pred))
print('Test accuracy score:', accuracy_score(y_test, test_pred))  # 输出

输出：

Train accuracy score: 0.9788732394366197
Test accuracy score: 1.0

测试数据集正确率100%

OneVsRestClassifier葡萄酒数据集

同上数据集

ovo = OneVsOneClassifier(lr_model)
ovo.fit(X_train, y_train)
# 拟合模型
ovo.fit(X_train, y_train)

# 预测训练集和测试集上的结果
train_pred1 = ovo.predict(X_train)
test_pred1 = ovo.predict(X_test)

# 输出准确率
print('Train accuracy score:', accuracy_score(y_train, train_pred1))
print('Test accuracy score:', accuracy_score(y_test, test_pred1))  

输出：
Train accuracy score: 0.9929577464788732
Test accuracy score: 1.0

测试数据集正确率100%