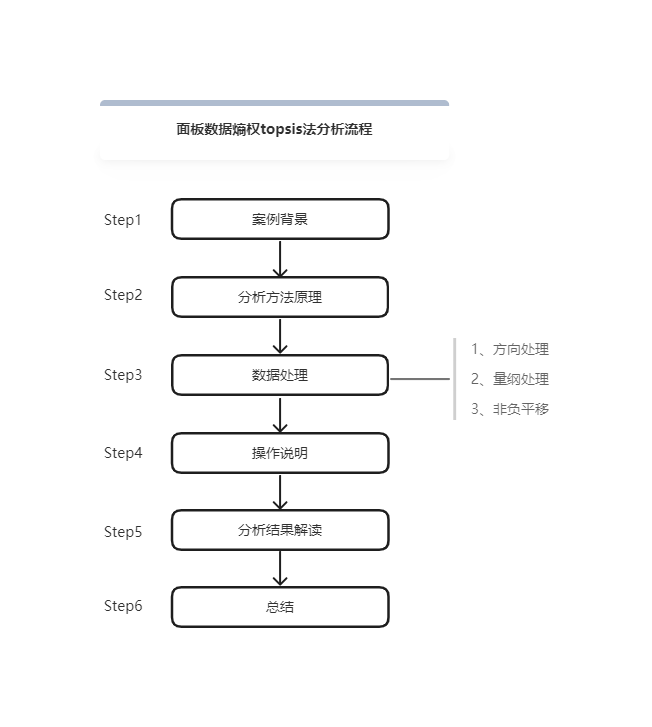
面板数据熵权topsis法分析流程
一、案例背景
当前有9家公司连续5年(2018-2022年)的财务指标数据,想要通过这份数据,确定9家公司的财务排名情况。因为各项财务指标的权重有所不同,所以选择使用熵权topsis法进行研究。
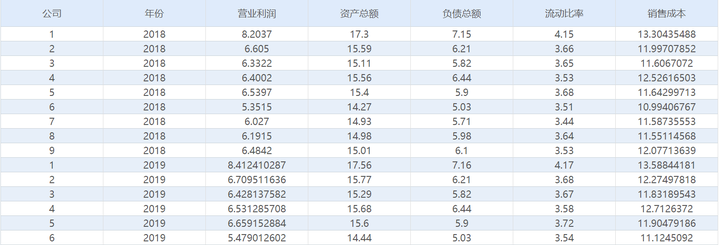
数据为9家公司连续5年的5个财务指标的数据,因为同时包含时间序列数据和截面数据,所以属于面板数据。应该有9*5=45行数据,5个财务指标各占一列,同时公司编号和年份各占一列,最后应该为45行*7列数据,最终应该将数据整理为如下格式:
二、分析方法原理
熵权法的基本原理是:指标的变异性越强,则离散程度越高,就会被赋予较大的权重,对评价目标的影响更显著。
topsis法的基本原理是:根据研究的各个目标距理想目标的愿景程度大小进行排序,从而实现对研究目标的优劣批评。
熵权topsis法包括熵权法和topsis法;使用熵权法计算各评价指标的权重,然后利用权重值乘原始数据,得到新数据,再利用新数据进行topsis法计算,最终进行各评价对象的优劣排序。
三、数据处理
使用熵权topsis法进行分析,需要对数据进行三个方面的处理,分别是方向处理、量纲处理以及对数据进行非负平移。接下来分别进行操作介绍。
(1)方向处理
5个财务指标分别为营业利润、资产总额、负债总额、流动比率、销售成本。这5个指标中既有正向指标(越大越好的指标,如利润),又有逆向指标(越小越好的指标,如成本)。熵权topsis法运算规则中,正向指标越大越好,逆向指标越小越好,所以需要对数据进行方向处理。
将正向指标“营业利润”、“资产总额”、“流动比率”使用SPSSAU进行正向化处理;将逆向指标“负债总额”、“销售成本”使用SPSSAU进行逆向化处理。
SPSSAU【生成变量】->正向化/逆向化->确认处理,操作如下图:
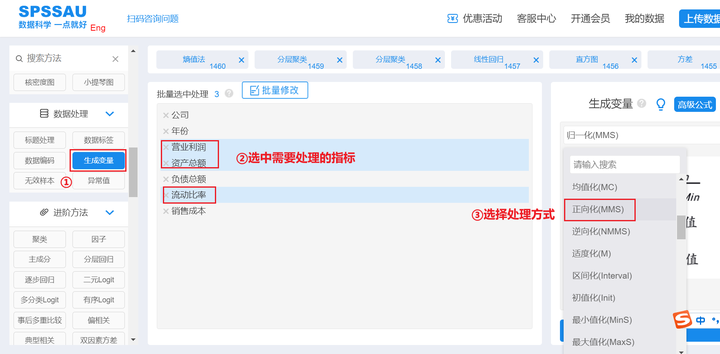
同理,将其他两个指标进行逆向化处理即可。
(2)量纲处理
消除数据方向的影响后,还需要消除由于数据单位不同造成的影响,即进行量纲处理,SPSSAU提供十几种量纲处理方法,常见的标准化处理方式有“归一化”将数据压缩在0到1之间;“区间化”将数据压缩在自己设定的区间内等等。研究人员可以结合参考文献和自己数据特征进行量纲处理方法选择。不同的处理方式可能会带来分析结果的不同,但是一般不会有太大偏差。
本案例因为上述分析中已经进行了正向/逆向此两种处理,而正向/逆向化处理可同时解决方向和量纲问题,所以不需要再次进行归一化处理。
(3)非负平移
数据进行归一化处理后,有些数据会出现等于0的情况,导致在利用熵值法求权重时取对数值无意义,影响研究结果,所以需要对评价指标进行非负化处理,使用SPSSAU生成变量的非负平移功能进行。SPSSAU默认平移值为“最小值的绝对值加上0.01”,研究人员可更换为0.001,0.0001,0.00001,0.1。
SPSSAU操作如下:
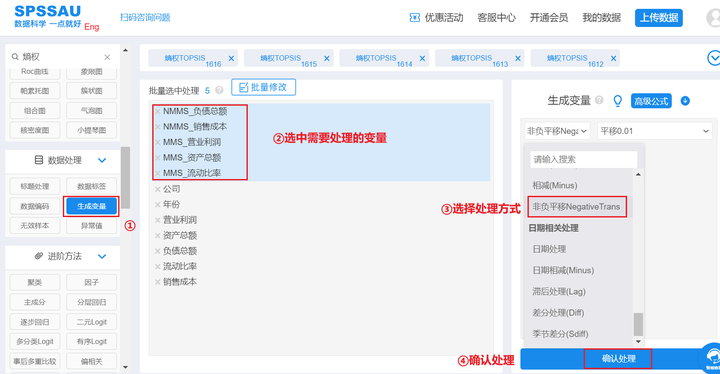
数据处理完成之后,接下来介绍如何使用SPSSAU进行面板数据熵权topsis法分析。
四、操作说明
面板数据熵权topsis法分析可以通过筛选年份,以年份为单位分别进行分析,最后取平均值作为最终分析结果。
分别筛选出2018-2022年的数据,进行5次熵权topsis法分析,操作如下:
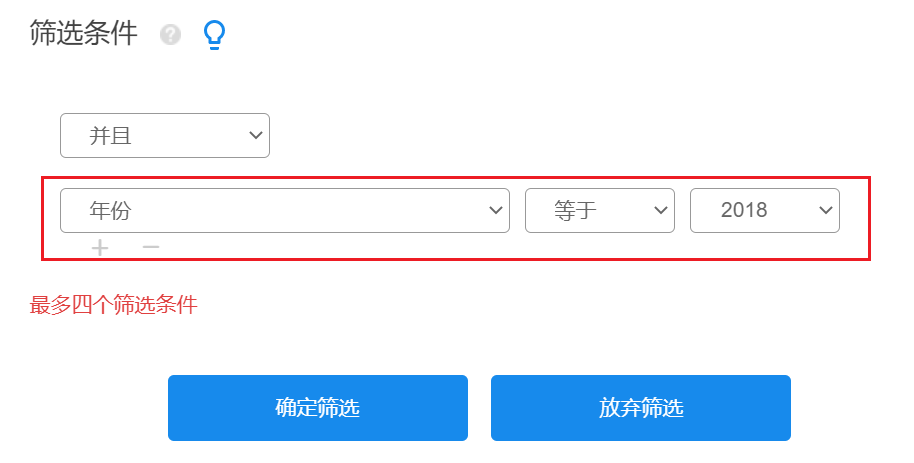
筛选后,SPSSAU->熵权topsis法,将指标拖拽到分析框中,点击开始分析即可,如下图:
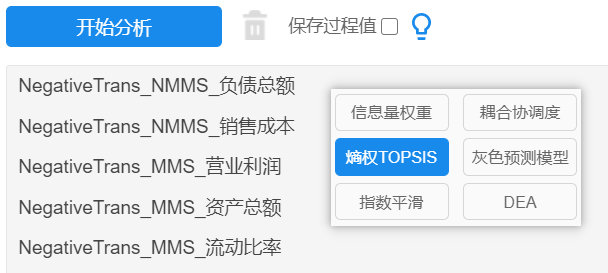
按照上述分析过程依次筛选5年的数据,进行5次分析,得到5次分析结果。
五、分析结果解读
熵权topsis法实际上为熵权法后得到新数据,然后用新数据进行TOPSIS法研究。所以会输出熵值法计算权重结果表和topsis法评价计算结果表。但是熵权topsis法核心是进行topsis法研究,最终要得到评价对象的排序,所以熵值法计算结果只作为中间计算过程,更重要的是关注topsis法分析结果。
SPSSAU输出2018年topsis评价计算结果如下表:
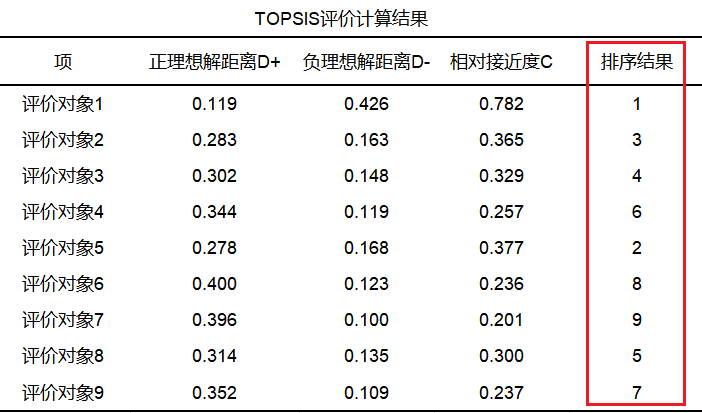
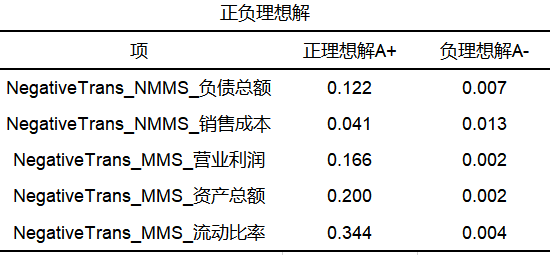
从上表来看,利用熵权法后加权生成的数据进行topsis法分析(SPSSAU算法自动完成),针对5个财务指标对9个公司的财务水平进行评价;topsis法首先找出评价指标的正负理想解A+和A-(中间计算过程,一般不关注),然后计算出各评价对象分别与正负理想解的距离D+和D-,最终计算得到各评价对象与最优方案的相对接近度C值,并针对C值进行排序。
上述为2018年一次熵权topsis法分析结果,面板数据将5次分析结果得到的相对接近度C值取平均值后进行排序,得到最终分析结果。
筛选年份后分别进行5次分析,将5年的相对接近度C值汇总整理如下表:
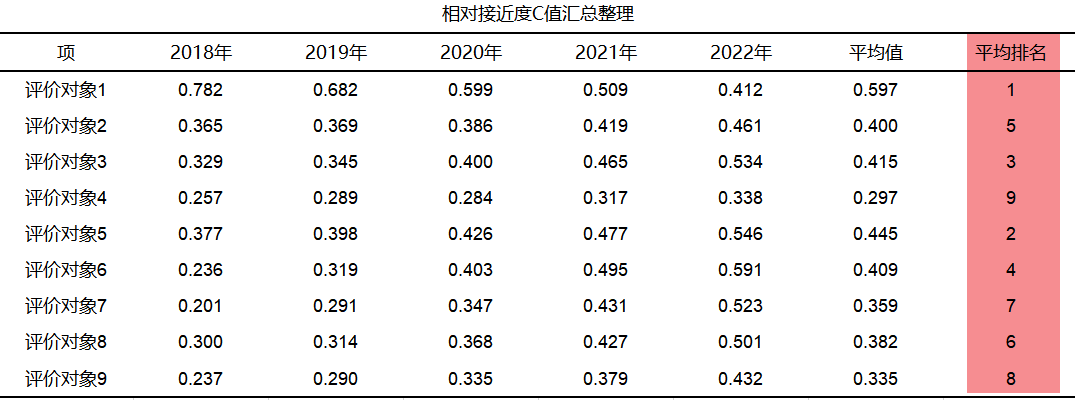
从上表汇总结果可以看出,评价对象1即公司1,他的相对接近度C值最高,说明公司1在财务指标上表现最优,其次是公司5,而公司4的相对接近度C值最低,在财务指标上表现最差。
六、总结
熵权topsis法是使用熵权法先得到指标权重,然后利用权重值乘原始数据得到新数据后,利用新数据进行topsis法分析,最终得到各评价对象的相对接近度C值,来判断和衡量各评价对象的优劣排序。分析依次需要对数据进行正向化/逆向化处理、标准化处理和非负平移。针对面板数据,需要依次筛选年份后,得到每年的相对接近度C值,最终通过计算平均值得到各评价对象的优劣排名情况。