题目-最小公倍数挑战 (51nod.com)

题意：

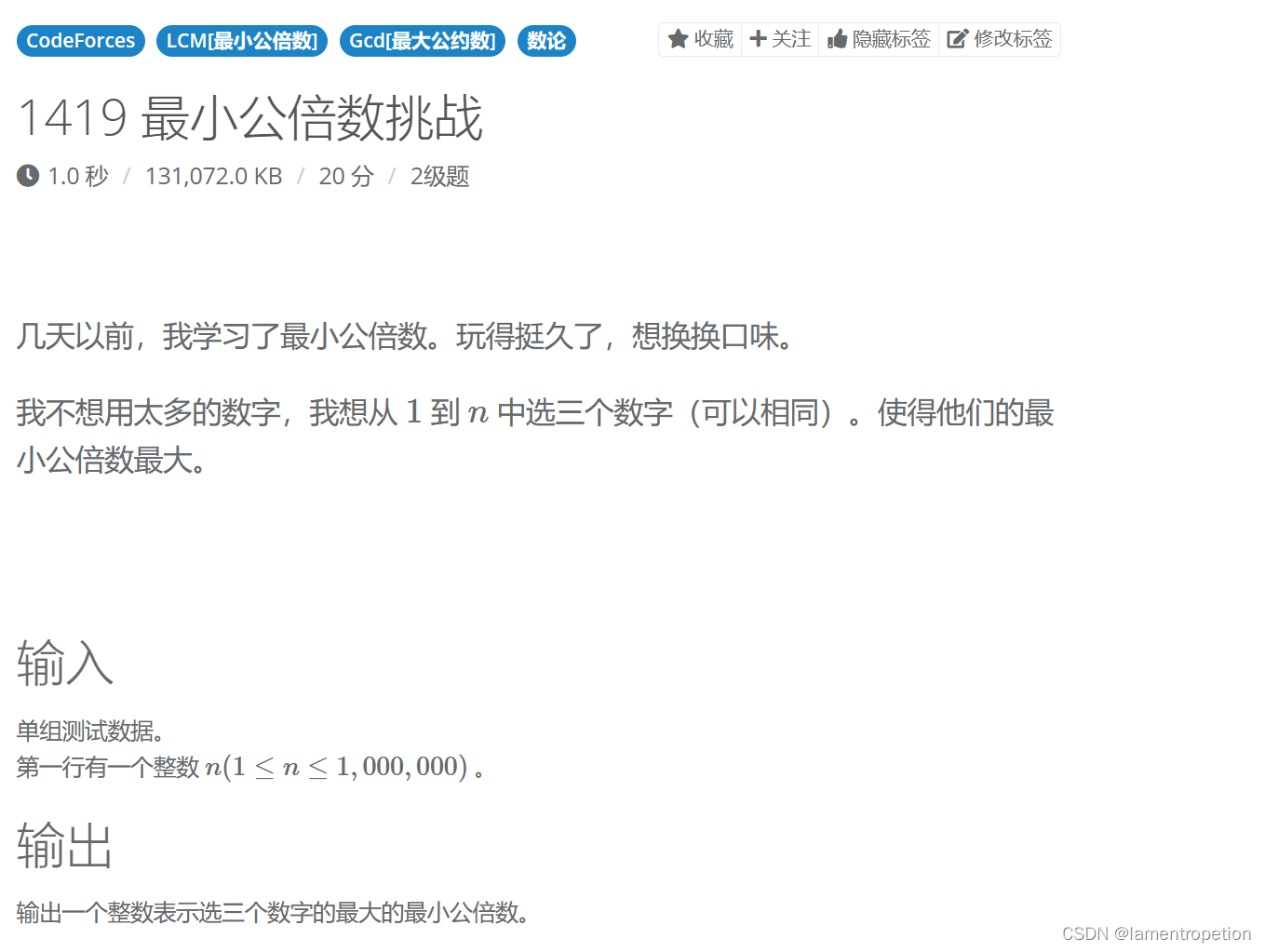
思路：

要找到三个数使得他们的lcm尽可能大

那就让这三个数都两两互质，且三个数的积尽可能大

若n为奇数，考虑n-1和n-2

n和n-1一定互质，那么考虑n和n-2是否互质

结论是：

n为奇数时，gcd(n,n-2)=1

n为偶数时，gcd(n,n-2)=2

这是为什么呢：

 

 所以d要不等于1，要不等于2

当n为奇数时d=1，当n为偶数时d=2

所以当n为奇数时，答案就是n*(n-1)*(n-2)

当n为偶数时：

因为gcd(n,n-2)=2，所以答案就是n*(n-1)*(n-2)/2

但是这个不一定是答案，还有别的解比它大的

考虑n-3：

当gcd(n,n-3)=1时，答案就是n*(n-1)*(n-3)

gcd(n,n-3)!=1时，答案就是(n-1)*(n-2)*(n-3)

对于gcd(n,n-3)也有性质：

gcd(n,n-3)<=3

证明方法也类似于上图

Code：

#include <bits/stdc++.h>

#define int long long

using namespace std;

int n;

void solve(){
	cin>>n;
	if(n==1) cout<<1<<'\n';
	else if(n==2) cout<<2<<'\n';
	else{
		if(n%2==1) cout<<n*(n-1)*(n-2)<<'\n';
		else{
			if(__gcd(n,n-3)==1) cout<<n*(n-1)*(n-3)<<'\n';
			else cout<<(n-1)*(n-2)*(n-3)<<'\n';
		}
	}
}
signed main(){
	int __=1;//cin>>__;
	while(__--)solve();return 0;
}