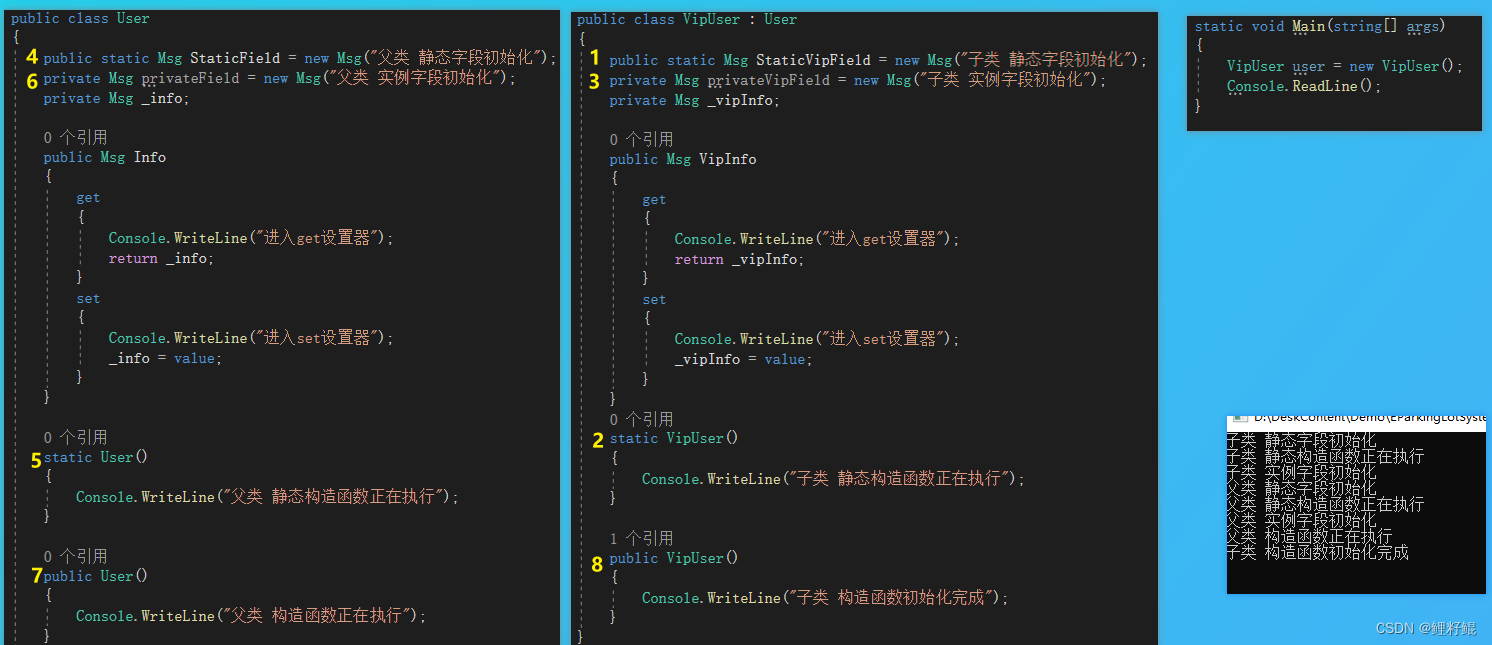
七、数学知识

（一）质数

1. 质数（素数） 的定义：
   
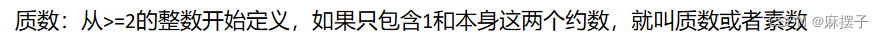
2. 互质的定义：除了1以外，两个没有其他共同质因子的正整数称为互质，比如3和7互质。因为1没有质因子，1与任何正整数（包括1本身）都是互质。
3. 约数（因数） 的定义：约数又称为因数。整数a除以整数b (b≠0) 除得的商正好是整数而没有余数，我们就说a能被b整除，或b能整除a。 a称为b的倍数，b称为a的约数。
4. 合数的定义：合数是指在>=2的整数中除了能被1和本身整除外，还能被其他正整数（0除外）整除的数。 与之相对的是质数，而1既不属于质数也不属于合数 。最小的合数是4。
5. 质因数的定义：质因数（素因数或质因子）在数论里是指能整除给定正整数的质数。
   （1）只有一个质因数的正整数为质数。
   举例：5只有1个质因数，5本身。（5是质数）
   （2）质因数就是一个数的约数，并且是质数。
   举例：8=2×2×2，2就是8的质因数，2既是质数又是约数；12=2×2×3，2和3就是12的质因数，2和3既是质数又是约数；
   （3）1没有质因数。
   2、4、8、16等只有1个质因子：2。（2是质数，4 =2²，8 = 2³，如此类推）
6. 定理1：一个合数n分解而成的质因数最多只包含一个大于$\sqrt{n}$的质因数。
   举例：$n=99=11\times 3^2$，其中11大于$\sqrt{99}$。
   反证法：若n可以被分解成两个大于$\sqrt{n}$的质因数,则这两个质因数相乘的结果大于n,与事实矛盾
7. 定理2：算术基本定理（唯一分解定理）：正整数的因数分解可将正整数表示为一连串的质因数相乘，任何一个大于 1 数都能分解为素数幂次方乘积的形式, 即每一个数n都能分解成
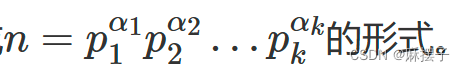
   质因数如重复可以用指数表示。根据算术基本定理，任何正整数皆有独一无二的质因数分解式。
   证明：证明: 若一个数是素数。定理显然成立。那么, 若一个数n是合数, 意味着它有因子, 即可以得到n=n1n2, 其中n1和n2都严格小于n。若n1和n2都不是素数。那按照同样的方式。n1和n2也可以各自分解为一些因子的乘积, 且因子都严格小于它们。那么, 由于n是有限的。到最后n只会分解成为$p{1}^{\alpha 1}$$p{2}^{\alpha 2}$…$p{k}^{\alpha }k$的形式。且p1
   , p2, … , pk都为素数(不全为素数的话就继续往下分)。(证毕)

例题1：试除法判定质数

题目 难度：简单
方法一：暴力，时间复杂度$O(n)$

bool isPrime(int x) 
{
  if (x < 2) return false;
  for (int i = 2; i < x; ++i)
  {
     if (a % i == 0) return false;
   }
  return true;
}

方法二：试除法
暴力做法其实已经很简单了，但是如果 x 是 a 的约数，那么 $\frac{a}{x}$也是 a 的约数。
所以对于每一对 $(x,\frac{a}{x})$，只需要检验其中的一个就好了。为了方便起见，我们之考察每一对里面小的那个数。不难发现，所有这些较小数就是$[1,\sqrt{a}]$ 这个区间里的数。因从时间复杂度从暴力法的$O(n)$，降到$O(\sqrt{n})$

#include<iostream>
using namespace std;

bool is_prime(int x)
{
    if(x<2) return false;
    for(int i=2;i<= x/i;i++)
    {
        if(x%i==0) return false;
    }
    return true;
}

int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int x;
        cin>>x;
            
        if(is_prime(x))
        cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
    return 0;
}

例题2：分解质因数。给定 n 个正整数 ai，将每个数分解质因数，并按照质因数从小到大的顺序输出每个质因数的底数和指数

题目 难度：简单
试除法：时间复杂度$O(\sqrt{n})$

#include <iostream>
#include <algorithm>

using namespace std;

void divide(int x)
{
    for (int i = 2; i <= x / i; i ++ )
    {
        if (x % i == 0)//说明i是x的因数。一个数除了1之外，他最小因数一定是质数，所以这里遇到的第一个能整除x的i一定是质数。
        {
            int s = 0;//指数
            while (x % i == 0) x /= i, s ++ ;//求i的指数s，比如x=10，i=2，s=1；x=10/2=5
            cout << i << ' ' << s << endl;
        }
    }
    if (x > 1) cout << x << ' ' << 1 << endl;
    //把这个最小质因数i1除干净了之后得到一个新的数x2
    //这个新的数x2的最小质因数i2肯定比之前的最小质因数i1大，因为比之前小的都被除干净了，同理新的数x2的最小因数又是质因数。
    //比如100=2*2*5*5，第一个最小质因数i1=2，除干净后得到新的数x2=25，这时i就从3开始for循环,得到新的数的最小质因数i2=5
    cout << endl;
}

int main()
{
    int n;
    cin >> n;
    while (n -- )
    {
        int x;
        cin >> x;
        divide(x);
    }
    return 0;
}

例题3：筛质数。给定一个正整数 n，请你求出 1∼n 中质数的个数。

题目 难度：简单

朴素筛法

1.做法：为了找出1~n中的质数，把 2 ~ (n-1)中的所有的数的倍数都标记上，最后没有被标记的数就是质数。
2.原理：假定有一个数p未被 2 ~ (p-1)中的数标记过，那么说明，不存在 2~(p-1)中的任何一个数的倍数是p，也就是说p不是 2 ~ (p-1)中的任何数的倍数，也就是说2 ~ (p-1)中不存在p的约数，因此，根据质数的定义可知：p是质数。
3.时间复杂度：当i=2时，循环了n/2次，当i=3时，循环了n/3次……当i=n时，循环了1次。所以
$n/2+n/3+n/4\dots \dots n/n=n(1/2+1/3+1/4\dots \dots +1/n)=n（lnn+c）$
调和级数:当n趋近于正无穷的时候，$1/2+1/3+1/4+1/5+\dots +1/n=lnn+c$
底数越大,log数越小，所以$nlog{e}^n<nlog{2}^n$
最后得到时间复杂度约为$O(nlogn)$。

#include<iostream>
using namespace std;

const int N=1e6+10;
int n;
bool tag[N];//用来打标记，默认是false
int prime[N];
int cnt=0;

void get_prime(int n)
{
    for(int i=2;i<=n;i++)
    {
        if (tag[i]==true) continue;//如果标记为true，直接进行下一次for循环
        prime[cnt++] = i;;//2，3，5，7，11……是质数，计入
        for(int j=i+i;j<=n;j+=i) tag[j]=true;//给j的倍数（2的倍数：4，6，8，12……。3的倍数：6，9，12，15……。）打上标签true，代表j的倍数是合数
    }
}

int main()
{
    cin>>n;    
    get_prime(n);
    
    cout<<cnt;
    return 0;
}

埃氏筛法

1.做法：为了找出 1 ~ n 中的质数，把 2 ~ (n-1) 中的所有素数的倍数都标记上，最后没有被标记的数就是1 ~ n 中的质数。
2.原理：在朴素筛法的过程中只用质数项去筛。
埃氏筛法的时间复杂度的简化来源于只需把素数的倍数删掉。这样的话就可以少筛很大一部分数。因为每个合数都是素数的倍数，比如$4=2\ast 2，6=2\ast 3，8=2\ast 4，9=3\ast 3$。
3.时间复杂度：是 $O(n\log \log n)$。
质数定理：1 ~ n中有$n/lnn$个质数。所以时间复杂度为$O(nlog(logn))$，粗略为$O(n)$。

#include<iostream>
using namespace std;

const int N=1e6+10;
int n;
bool tag[N];//用来打标记，默认是false
int prime[N];
int cnt=0;

void get_prime(int n)
{
    for(int i=2;i<=n;i++)
    {
        if (tag[i]==false) //等于false代表就是质数，先给出一个if的判断条件就是为了找出质数项
        {
            primes[cnt++] = i;
            for (int j = i; j <= n; j += i) tag[j] = true;//(2，4，6，8，10，12，14，16，18……是true，3,6,9,12,15,18,……是true)
        }
    }
}

int main()
{
    cin>>n;    
    get_prime(n);
    
    cout<<cnt;
    return 0;
}

线性筛法

1.做法：埃式筛法的缺陷在于，对于同一个合数，可能被筛选多次。为了确保每一个合数只被筛选一次，我们用每个合数的最小质因子来进行筛选，也就是线性筛法。比如15会被3的5倍筛一次, 会被5的三倍筛一次。这样的话就筛了2次。
1.把每个数都被它的最小质因子筛掉
2.每个数有且仅有一个最小质因子
3.所以每个数只会被筛一次
4.因而它是线性的
2.原理：1 ~ n之内的任何一个合数一定会被筛掉，而且筛的时候只会被最小质因子来筛。 每一个数都只有一个最小质因子，所以每个数都只会被筛一次，因此线性筛法是线性的。

• 首先说明：$primes[j]\times i$的最小质因子应该是 $min$($primes[j]$，$i$的最小质因子），即二者中的最小值。
  当 $i$ % $primes[j]\ne 0$ 时，说明此时 $primes[j]$小于 i的所有质因子，因为 $primes[j]$ 是从小到大进行枚举的，如果 $primes[j]$是 i 的质因子之一，那么应该满足 $i$ % $primes[j]=0$ 才对。所以此时 $primes[j]$是 $primes[j]\times i$的最小质因子
  当 $i$ % $primes[j]=0$时，说明此时 $primes[j]$是 $i$的最小质因子（因为 $primes[j]$ 是从小到大进行枚举的），所以此时$primes[j]$ 也是 $primes[j]\times i$的最小质因子
  综上，使用 $primes[j]$ 来筛选 $primes[j]\times i$ 是可行的，因为两种情况下 $primes[j]$都是 $primes[j]\times i$ 的最小质因子

• 循环应该在$i$ % $primes[j]==0$的时候中止，理由如下：
  当 $i$% $primes[j]=0$ 的时候如果不中止，那么将进入下一次循环，下一次循环要筛掉的数字是 $primes[j+1]\times i$。对于 $primes[j+1]\times i$，$i$的值没有变，和上一步满足 $i$% $primes[j]=0$时的 $i$是一样的，所以当前 i的最小质因子仍为 primes[j]；但是当前为 $primes[j+1]$，即比上一次循环的 $primes[j]$要大，那么此时 $primes[j+1]$ 和 $i$的最小质因子 ($primes[j]$)相比，较小值为 i的最小质因子 ($primes[j]$)，所以 $primes[j+1]\times i$的最小质因子应该为 ($primes[j]$)，那么$primes[j+1]\times i$这个数应该由 ($primes[j]$)来筛选掉，但是当前却是由 ($primes[j+1]$)筛选掉的，所以出现了重复筛选。因此，为了保证所有数只被筛选一次，循环需要在 i % $primes[j]==0$的时候中止。

#include<iostream>
using namespace std;

const int N=1e6+10;
int n;
bool tag[N];//用来打标记，默认是false质数
int prime[N];
int cnt=0;

void get_prime(int n)
{
    for(int i=2;i<=n;i++)
    {
        if (tag[i]==false) prime[cnt++] = i;//prime[]里面放的是质数
        for(int j=0;i*prime[j]<=n;j++)
        {
            tag[i*prime[j]]=true;//true   i*prime[j]是合数
            //i是质数就筛掉i与prime[]中所有质数的乘积（是合数）;i是非质数筛掉i与（primes中所有 <= i的最小质因子）的乘积（是合数）。比如18只会在枚举到i==9的时候，primes[j=0] == 2，这时候被筛掉，接下来primes[j=1] == 3，筛掉27，然后break。
            if (i % prime[j] == 0) break;//意味着prime[j]是i的最小质因子，因为prime是从小到大枚举的
        }
    }
}

int main()
{
    cin>>n;
    
    get_prime(n);
    cout<<cnt;
    return 0;
}

（二）约数

例题4：试除法求约数

题目 难度：简单
时间复杂度：$O(\sqrt{n})$

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

int n;
vector<int> get_divisors(int x)
{
    vector<int> res;
    for(int i=1;i<=x/i;i++)
    {
        if(x%i==0) 
        {
            res.push_back(i);
            if(i!=x/i) res.push_back(x/i);
        }
    }
    sort(res.begin(),res.end());
    return res;
}

int main()
{
    cin>>n;
    while(n--)
    {
        int x;
        cin>>x;
        auto res=get_divisors(x);
        for(auto t:res) cout<<t<<" ";
        //res.clear();
        cout<<endl;
    }    
    return 0;
}

例题5：约数个数

由于算数基本定理：

比如：18=1×2×3×3=2×3^2。所以约数有1，2，3，6，9，18，约数个数为（1+1）×（2+1）。
为什么要加1：因为对于2×3^2来说。2这个位置有两种选择（0，1），3这个位置有三种选择（0，1，2）；
题目 难度：简单

#include<iostream>
using namespace std;
#include<unordered_map>
typedef long long LL;

const int N = 110, mod = 1e9 + 7;
long long res=1;//个数

int main()
{
    int n;
    cin >> n;
    unordered_map<int, int> primes;
    
    while(n--)
    {
        int x;
        cin>>x;
        for(int i=2;i<=x/i;i++)
        {
            while (x % i == 0)//说明i是x的质约数
            {
                x=x/i;
                primes[i]++;//i是质因子，primes[i]是指数
            }
        }
        if(x>1) primes[x]++;
    }
    for(auto p:primes) res=res*(p.second+1)%mod;
    cout<<res<<endl;
    return 0;
}

补充：
unordered_map是C++中的哈希表，可以在任意类型与类型之间做映射。

基本操作

• 引用头文件(C++11)：#include <unordered_map>

• 定义：unordered_map<int,int> hash；unordered_map<string, double> hash …

• 插入：例如将(“ABC” -> 5.45) 插入unordered_map<string, double> hash中，hash[“ABC”]=5.45

• 查询：hash[“ABC”]会返回5.45

• 判断key是否存在：hash.count(“ABC”) != 0
  或 hash.find(“ABC”) //返回值：如果给定的键存在于unordered_map中，则它向该元素返回一个迭代器，否则返回映射迭代器的末尾hash.end()。

• 遍历
  for (auto &item : hash)
  {
  cout << item.first << ’ ’ << item.second << endl;
  }
  for (unordered_map<string, double>::iterator it = hash.begin(); it != hash.end(); it ++ )
  {
  cout << it->first << ’ ’ << it->second << endl;
  }

例题6：约数之和

题目 难度：简单

#include<iostream>
#include<unordered_map>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long LL;

const int mod = 1e9 + 7;

int main()
{
    int n;
    cin >> n;
    unordered_map<int, int> primes;
    
    while(n--)
    {
        int x;
        cin>>x;
        for(int i=2;i<=x/i;i++)
        {
            while (x % i == 0)//说明i是x的质约数
            {
                x/=i;
                primes[i]++;//i是质因子，primes[i]是指数
            }
        }
        if(x>1) primes[x]++;
    }
    //for(auto prime:primes) cout<<prime.first<<" "<<prime.second<<endl;
    LL res=1;//约数之和
    for(auto p : primes) 
    {
        LL b=p.first;
        LL a=p.second;//first里面放的是质因数，second里面放的是指数
        LL t=1;//p的0次方
        while(a--) t=(t*b+1)%mod;//t=(p+1)p+1=p^2+p+1;t=(p^2+p+1)p+1
        res=res*t%mod;
    }
    cout<<res<<endl;
    return 0;
}

例题7：最大公约数

题目 难度：简单
欧几里得算法（辗转相除法）
定理1：d能整除a且d能整除b，那么d就能整除ax+by；

定理2：$gcd(a,b)==gcd(b,amodb)==gcd(b,a-c\times b)$
证明：由定理1可得，$amodb=a-(a/b)\times b=a-c\times b$//a/b就是a整除b=c，也就是c是整数。
因为d能整除a且d能整除b，那么d就能整除a-c×b，那么d就能整除a-c×b+c×b

#include<iostream>
using namespace std;

int gcd(int a,int b)
{
    return b?gcd(b,a%b):a;//b为真执行gcd(b,a%b);b为假执行return a
    //比如a=4,b=6;gcd(b,a%b)==gcd(6,4)==gcd(4,2)==gcd()
}

int main()
{
    int n;
    cin>>n;
    while(n--)
    {
        int a,b;
        cin>>a>>b;
        cout<<gcd(a,b)<<endl;
    }
    return 0;
}

（三）裴蜀定理

裴蜀定理，又称贝祖定理（Bézout’s lemma），是一个关于最大公约数的定理。
定理1： 设 a,b 是不全为零的整数，则存在整数 x,y, 使得 $ax+by=gcd(a,b)$。举例$gcd(2,6)=2=-2\ast 2+1\ast 6$。
定理2： 如果 a 与 b 互质，那么一定存在两个整数 x 与 y，使得 ax+by=1.
进一步结论：
设自然数 a、b 和整数 n。a 与 b 互素。考察不定方程：$ax+by=n$
其中 x 和 y 为自然数。如果方程有解，称 n 可以被 a、b 表示。
记 $C=ab-a-b$。由 a 与 b 互素，C 必然为奇数。则有结论：对任意的整数 n，$n$ 与 $C-n$ 中有且仅有一个可以被表示。即：可表示的数与不可表示的数在区间 $[0,C]$ 对称（关于 C 的一半对称）。0 可被表示，C 不可被表示；负数不可被表示，大于 C 的数可被表示。举例：a=4，b=7，C=17，那么1不可以被表示，但是16可以被表示，5不可以被表示，但是12可以被表示。
而且如果 a,b均是正整数且互质，那么由 ax+by,x≥0,y≥0不能凑出的最大数是 C=ab−a−b。

例题8：买不到的数目

题目 难度：中等

八、动态规划

（一）背包问题

1.01背包问题

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次，第 i 件物品的体积是 vi，价值是 wi。求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

例题9：01背包问题

题目 难度：简单

方法一：二维dp数组法

1. 确定dp数组以及下标的含义：$dp[i][j]$代表 在背包承重为 j 的前提下，从前 i 个物品中选能够得到的最大价值是多少。 不难发现$dp[N][M]$ 就是本题的答案。
2. 确定递推公式，我们可以将它划分为以下两部分：
   （1）不选第 i 个物品：意味着从前 i−1 个物品中选且总重量不超过 j ，这种情况的最大价值为 $dp[i-1][j]$。
   （2）选第 i 个物品时的最大价值为（也就是背包容量 j 减去物品 i 的容量 $w[i]$所能放的最大价值后再加上第 i 个物品的价值，也就是$dp[i-1][j-w[i]]$再加上物品 i 的价值$v[i]$）：$dp[i-1][j-w[i]]+v[i]$（物品$i$的价值）就是背包放物品$i$得到的最大价值。

结合以上两点可得递推公式：
$dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])$

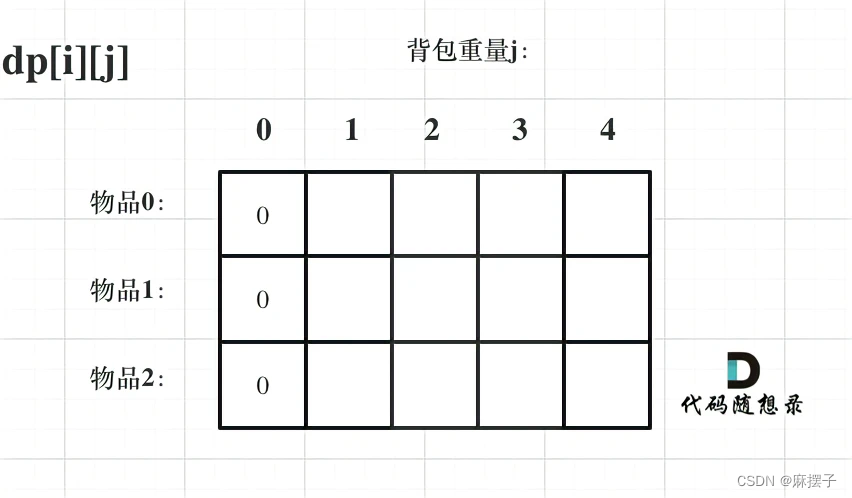
3. dp数组如何初始化
   首先从$dp[i][j]$的定义出发，如果背包容量j为0的话，即$dp[i][0]$，无论是选取哪些物品，背包价值总和一定为0。如图:
   
4. 确定遍历顺序（两层for循环）
   先遍历物品还是先遍历背包重量呢？其实都可以！但是先遍历物品更好理解
5. 将所有的情况遍历出来如下图所示
   紫色的是初始化默认值0。红色的是代表j<v[i]，这个表格的值直接沿用上一个表格的值
   

#include <iostream>
using namespace std;

const int N=1000+10;
const int V=1000+10;

int n,m;
int v[N];//物体体积
int w[N];//物体价值
int dp[N][V];

int main()
{
    cin>>n>>m;
    
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];//分别输入物品1，2，3，4……的体积和价值
    
    //初始化：一开始都是0，尤其是当背包的容量为0时：dp[i][0]=0;
    
    for(int i=1;i<=n;i++)//i代表背包里面装的物品,先遍历物品
    {
        for(int j=0;j<=m;j++)
        {
            dp[i][j]=dp[i-1][j];
            if(j>=v[i]) dp[i][j]=max(dp[i][j],dp[i-1][j-v[i]]+w[i]);
        }
    }
    /*for(int i=1;i<=n;i++)//i代表背包里面装的物品
    {
        for(int j=0;j<=m;j++)
        {
            cout<<dp[i][j]<<" ";
        }
        cout<<endl;
    }*/
    cout<<dp[n][m]<<endl;
    return 0;
}

方法二：一维dp数组法

二维转化为一维：删掉了第一维：在前i个物品中取。f[j]表示：拿了总体积不超过j的物品，最大总价值。

1. 为何能转化为一维？
   对于每次循环的下一组$i$，只会用到$i-1$来更新当前值，不会用到$i-2$及之前值。于是可以在这次更新的时候，将原来的更新掉，反正以后也用不到。所以对于$i$的更新，只需用一个数组，直接覆盖就行了。
2. 如何转化为一维呢？ 只用一个数组，每次都覆盖前面的数组。
   （1）如果当前位置的东西不拿的话，和前一位置的信息（原来$i-1$数组的这个位置上的值）是相同的，所以不用改变。
   （2）如果当前位置的东西拿进背包的话，需要和前一位置的信息（原来$i-1$数组的这个位置上值）取max。
   二维时的更新方式：$dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i])$。去掉$i$这一层后$dp[j]=max(dp[j],dp[j-v[i]]+w[i])$，所以更新方式就为：$dp[j]=max(dp[j],dp[j-v[i]]+w[i])$;
   问题就在于：假如还是计算$dp[j]$，同样的想要计算$j$还是要基于$j-v[i]$，此时元素个数是 $i$，由之前的二维模式可以知道要计算$dp[i][j]$需要基于$dp[i-1][j-v[i]]$来求得。当$j$从小到大递增时，每次$j$都可以基于$j-v[i]$算出来，但是忽略了一个问题：当$j$从小到大递增时，$i$是不变的，也就是说基于$j-v[i]$求出来的$j$都是同一个$i$。
   如果$j$是降序的，也就是说当计算$j$时，$j-v[i]$还没有被更新（$j-v[i]<j$）。
   也就是说此时的 $j-v[i]$对应的还是上一轮的$i-1$，正好可以满足需求，所以$j$只能是从大到小来遍历。

#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int f[N];
int v[N], w[N];
int n, m;
int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++) {
        for (int j = m; j >= v[i]; j--) {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }
    cout << f[m] << endl;
}

2.完全背包问题

有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。第 i 种物品的体积是 $v[i]$，价值是 $w[i]$。求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

例题10：完全背包问题

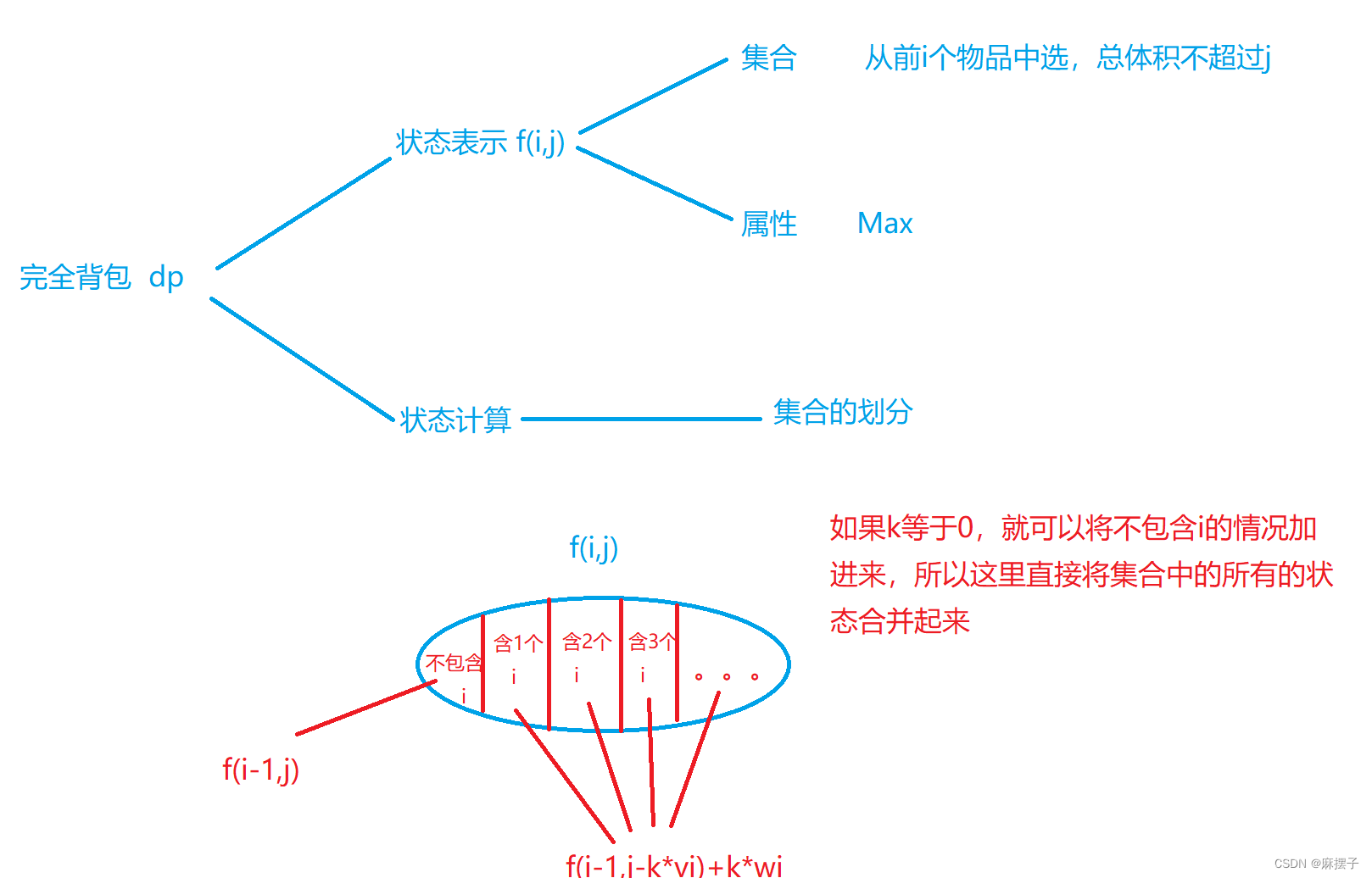
二维数组法（会超时）

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int dp[N][N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            dp[i][j]=dp[i-1][j];//先不加入物品i时的最大价值是多少
            for(int k = 1 ; k * v[i] <= j ; k ++ )//加入物品i后，同一个物品i的数量是k
            {
                if(j>=k*v[i]) dp[i][j]=max(dp[i][j],dp[i-1][j-k*v[i]]+w[i]*k);
            }
        }        
    }           
    cout<<dp[n][m];
    return 0;
}

一维数组法

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int dp[N];

int main()
{
    cin >> n >> m;
    cin.tie(0);
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
    
    for(int i=1;i<=n;i++)
    {
        for(int j=v[i];j<=m;j++)
        {
            dp[j]=max(dp[j],dp[j - v[i]] + w[i]);
        }        
    }           
    cout<<dp[m];
    return 0;
}

（二）线性DP

递推方程有明显的线性关系

例题11：数字三角形

题目 难度：简单
如下图所示：（右下改成右上）

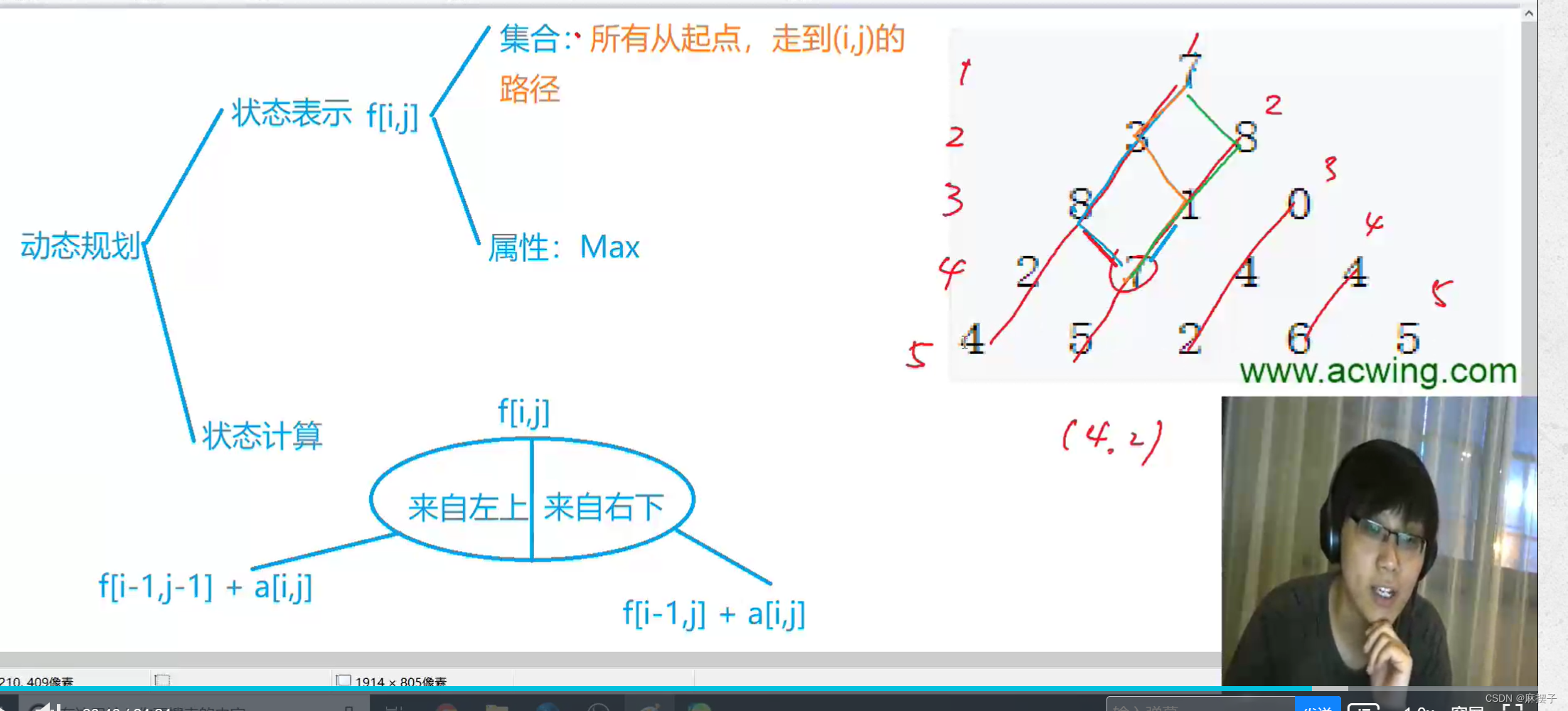
递推式为： $f[i][j]=max(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j])$，其中$a[i][j]$是每个点上的值，$f[i][j]$是点$（i,j）$到起点$（1,1）$的路径最大值，所以$f[1][1]=a[1][1]=7$。

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 510, INF = 1e9;
int n;
int a[N][N];
int f[N][N];

int main()
{
    cin>>n;
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= i; j ++ )
            cin>>a[i][j];

    for (int i = 0; i <= n; i ++ )
        for (int j = 0; j <= i + 1; j ++ )
            f[i][j] = -INF;
            //初始化是为了以后第一次找到值可以替换，设最大负数是因为每个f的值结果可能为负数，要想被替换只能刚开始就是最大负数

    f[1][1] = a[1][1];
    for (int i = 2; i <= n; i ++ )
        for (int j = 1; j <= i; j ++ )
            f[i][j] = max(f[i - 1][j - 1] + a[i][j], f[i - 1][j] + a[i][j]);

    int res = -INF;
    for (int i = 1; i <= n; i ++ ) res = max(res, f[n][i]);

    cout<<res;
    return 0;
}

例题12：三角形中最小路径之和

题目 难度：中等

class Solution {
public:
    int minimumTotal(vector<vector<int>>& triangle) 
    {
        //递推公式：f[i][j]=min(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j])

        //先给f[i][j]赋初值
        int n=triangle.size();//三角形有多少行
        const int INF=1e9;

        vector<vector<int>> f(n,vector<int>(n));    

        for(int i=0;i<n;i++)
        {
            for(int j=0;j<n;j++)
            {
                f[i][j]=INF;
            }
        }
        f[0][0]=triangle[0][0];

        // //递推
        for(int i=1;i<n;i++)
        {
            for(int j=0;j<=i;j++)
            {
                if(j==0) f[i][0]=f[i-1][0]+triangle[i][0];               
                else if(j==i) f[i][i]=f[i-1][i-1]+triangle[i][i];
                else f[i][j]=min(f[i-1][j-1]+triangle[i][j],f[i-1][j]+triangle[i][j]);
            }
        }   
        return *min_element(f[n-1].begin(),f[n-1].end());
    }
};

（三）打家劫舍系列

例题13：打家劫舍

class Solution {
public:
    int rob(vector<int>& nums) 
    {
        //递推公式：dp[i]=max(dp[i-2]+nums[i],dp[i-1])
        //dp[i]是指从0号到i号房间偷的最大现金,i最大=n-1；
        int n=nums.size();
        if (n == 0) return 0;//没有房间，没钱可偷
        if (n == 1) return nums[0];

        vector<int> dp(n,0);
        dp[0]=nums[0];
        dp[1]=max(nums[0],nums[1]);

        for(int i=2;i<n;i++) 
        {
            dp[i]=max(dp[i-2]+nums[i],dp[i-1]);
        }
        
        return dp[n-1];
    }
};

九、前缀和和差分

（一）一维前缀和

例题12：前缀和

题目 难度：简单

#include <iostream>
using namespace std;

const int N = 100010;
int n, m;
int a[N], s[N];

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) s[i]=s[i-1]+a[i];
    
    while(m--)
    {
        int l,r;
        cin>>l>>r;
        cout<<s[r]-s[l-1]<<endl;
    }
    return 0;
}

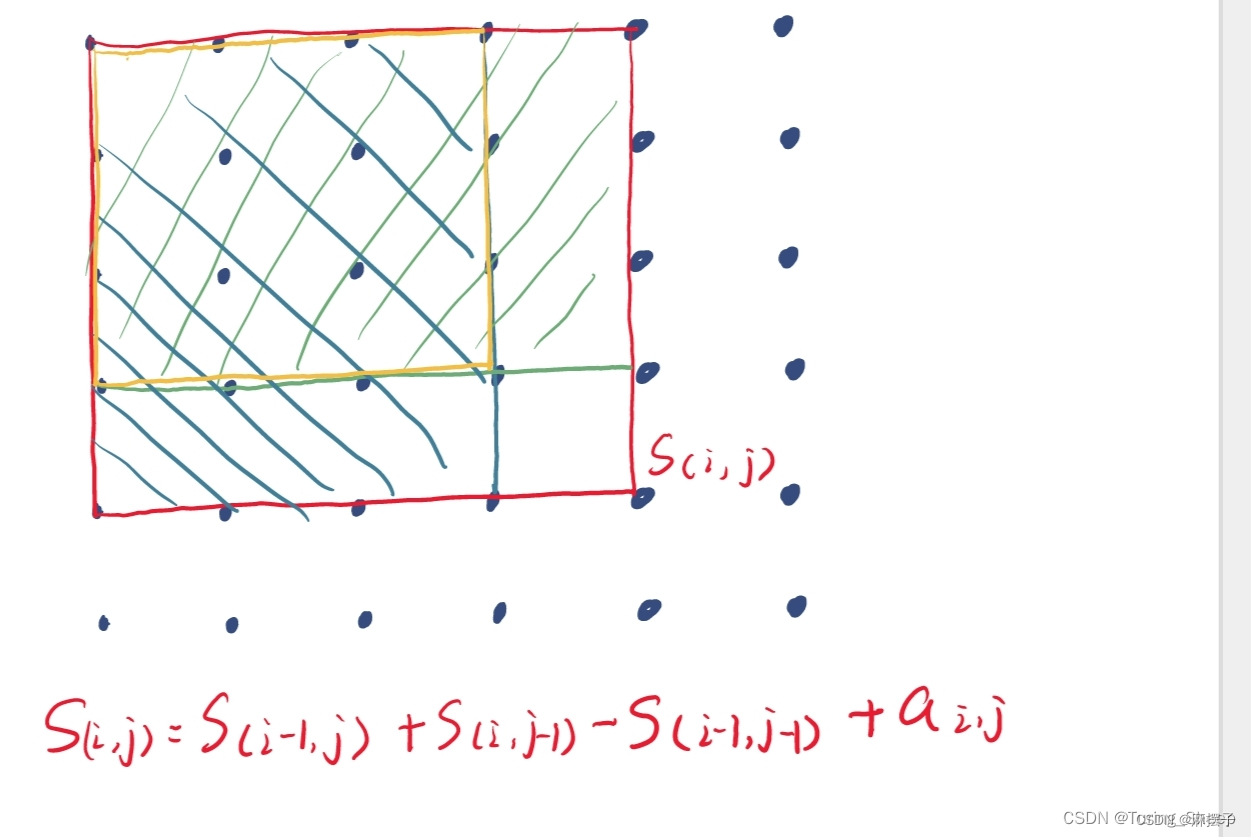
（二）二维前缀和

如下图所示求前缀和：绿色的加蓝色的减去黄色的再加上aij这个点

如下图所示求部分和

#include<iostream>
using namespace std;

const int N=1010;
int a[N][N];
int s[N][N];

int main()
{
    int n,m,q;
    cin>>n>>m>>q;
    
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            cin>>a[i][j];
            
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1]+a[i][j];//求前缀和
    
    while(q--)
    {
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        
        cout<<s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]<<endl;//算部分和
    }
    
    return 0;
}