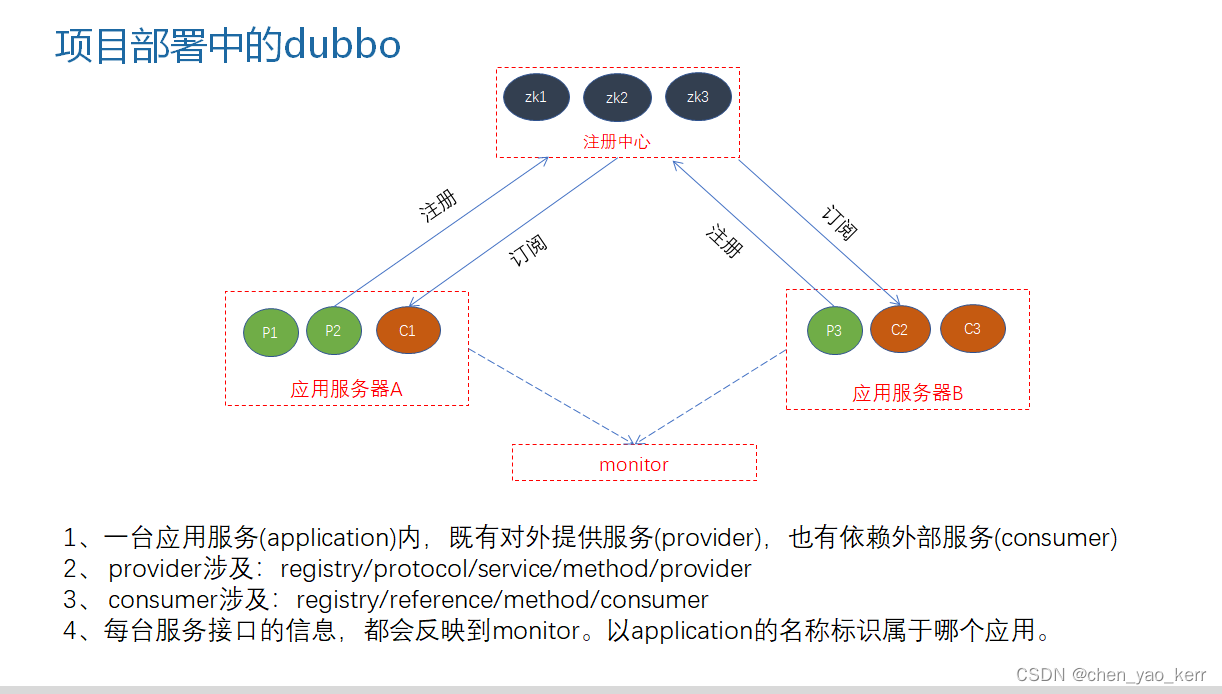
定义二叉树结点和树结点结构体： 

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef int BTDataType;
typedef int TDataType;

//二叉树
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;

//树
typedef struct TreeNode
{
	struct TreeNode* leftchild; //左孩子
	struct TreeNode* rightbrother; //右兄弟
	TDataType data;
}TNode;

 

一.删除二叉树中的结点

1.思想：

（1）首先判断要删除的结点是否存在，如果不存在则直接返回 NULL。
（2）如果要删除的结点小于当前结点，则递归删除左子树中的结点。
（3）如果要删除的结点大于当前结点，则递归删除右子树中的结点。
（4）如果要删除的结点等于当前结点，则分四种情况进行处理：
情况1：要删除的结点是叶子结点，直接删除即可。
情况2：要删除的结点只有右子树，将右子树替换当前结点即可。
情况3：要删除的结点只有左子树，将左子树替换当前结点即可。
情况4：要删除的结点既有左子树又有右子树，将右子树中的最小值替换当前结点即可。
最后返回删除结点后的二叉排序树的根节点。

2.代码实现

//查找二叉排序树中的最小值结点
BTNode* FindMin(BTNode* root) 
{
	if (root == NULL) 
	{
		return NULL;
	}
	else if (root->left == NULL) 
	{
		return root;
	}
	else 
	{
		return FindMin(root->left);
	}
}


//二叉树删除结点
BTNode* DeleteBTNode(BTNode* root, BTDataType data)
{
	//查找该结点
	if (root == NULL) 
	{
		return NULL;
	}
	else if (data < root->data)
	{
		root->left = DeleteBTNode(root->left, data);
	}
	else if (data > root->data) 
	{
		root->right = DeleteBTNode(root->right, data);
	}
	else 
	{
		//找到要删除的结点
		if (root->left == NULL && root->right == NULL) 
		{
			//情况1：要删除的结点是叶子结点
			free(root);
			root = NULL;
		}
		else if (root->left == NULL) 
		{
			//情况2：要删除的结点只有右子树
			BTNode* temp = root;
			root = root->right;
			free(temp);
		}
		else if (root->right == NULL) 
		{
			//情况3：要删除的结点只有左子树
			BTNode* temp = root;
			root = root->left;
			free(temp);
		}
		else 
		{
			//情况4：要删除的结点既有左子树又有右子树
			BTNode* temp = FindMin(root->right);
			root->data = temp->data;
			root->right = DeleteBTNode(root->right, temp->data);
		}
	}
	return root;
}

二.实现树与二叉树的相互转换

二叉树转换成树：

将二叉树的左孩子变成树的左孩子

将二叉树的右孩子变成树的右兄弟

树转换成二叉树：

将树的左孩子变成二叉树的左孩子，

将树的右兄弟变成二叉树的右孩子

//二叉树转换成树
TNode* ExchangeToTree(BTNode* root)
{
	if (root == NULL)
	{
		return NULL;
	}
	else
	{
		TNode* troot = (TNode*)malloc(sizeof(TNode));
		troot->data = root->data;
		troot->leftchild = ExchangeToTree(root->left);
		troot->rightbrother = ExchangeToTree(root->right);
		return troot;
	}
}

//树转换成二叉树
TNode* ExchangeToBinaryTree(TNode* troot)
{
	if (troot == NULL)
	{
		return NULL;
	}
	else
	{
		BTNode* root = (BTNode*)malloc(sizeof(BTNode));
		root->data = troot->data;
		root->left = ExchangeToBinaryTree(troot->leftchild);
		root->right = ExchangeToBinaryTree(troot->rightbrother);

		return root;
	}

}

三.实现二叉树/二叉排序树基本运算

//二叉排序树
//初始化
void InitBinaryTree(BTNode** root)
{
	*root = NULL;
}

//二叉排序树插入结点
void CreateBinaryTree(BTNode** root, BTDataType x)
{
	//走到空结点，即插入
	if ((*root) == NULL)
	{
		(*root) = (BTNode*)malloc(sizeof(BTNode));
		(*root)->data = x;
		(*root)->left = NULL;
		(*root)->right = NULL;
		return;
	}

	//已有该数据，即返回
	if (x == (*root)->data)
	{
		printf("已有该数据\n");
		return;
	}
	//小于该结点的数据，则往左走
	else if(x < (*root)->data)
	{
		CreateBinaryTree(&((*root)->left), x);
	}
	//大于该结点的数据，则往右走
	else 
	{
		CreateBinaryTree(&((*root)->right), x);
	}
}

//二叉排序树关键字key的查找长度
int FindBinaryTree(BTNode* root, BTDataType key)
{
	//走到空，返回
	if (root == NULL)
	{
		return;
	}
	//查找到key，则计数+1
	if (root->data == key)
	{
		return 1;
	}
	//递归查找
	if (key < root->data)
	{
		return FindBinaryTree(root->left, key) + 1;
	}
	if (key > root->data)
	{
		return FindBinaryTree(root->right, key) + 1;
	}
}

//二叉排序树中，打印a,b两个结点的公共祖先
BTNode* PublicAncestors(BTNode* root, BTDataType a, BTDataType b)
{
	if (root == NULL)
	{
		return NULL;
	}
	//a,b都在root的左子树
	if (a < root->data && b < root->data)
	{
		return PublicAncestors(root->left, a, b);
	}
	//a,b都在root的右子树
	if (a > root->data && b > root->data)
	{
		return PublicAncestors(root->right, a, b);
	}
	//a，b分别在root的左右子树，说明root就是a,b的祖先结点
	else
	{
		return root;
	}
}

//二叉树前序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}

//二叉树中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}

//二叉树后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}


//二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	//结点为空则返回0，否则返回结点的左子树结点个数＋结点的右子树结点个数＋1（结点本身是1个）
	return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

//二叉树叶子结点的个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	//是叶子结点则返回1，否则返回结点的左子树的叶子结点个数+结点的右子树的叶子结点个数
	return (root->left == NULL && root->right == NULL) ? 1 : 
		BinaryTreeLeafSize(root->left)
		+ BinaryTreeLeafSize(root->right);
}

//二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	assert(k > 0);
	if (root == NULL)
	{
		return 0;
	}

	if (k == 1)
	{
		return 1;
	}
	
	return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
	
}

//二叉树深度/高度
int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int leftDepth = BinaryTreeDepth(root->left);
	int rightDepth = BinaryTreeDepth(root->right);

	return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

//二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}

	if (root->data == x)
	{
		return root;
	}

	BTNode* leftRet = BinaryTreeFind(root->left, x);
	if (leftRet)
	{
		return leftRet;
	}
	BTNode* rightRet = BinaryTreeFind(root->right, x);
	if (rightRet)
	{
		return rightRet;
	}

	return NULL;
}


//计算二叉树的最大宽度
int BinaryTreeWidthMax(BTNode* root)
{
	assert(root);
	//记录二叉树的深度
	int depth = BinaryTreeDepth(root);
	int i = 1;
	int max = 1;
	while (i <= depth)
	{
		//复用接口，tmp 为每层的结点数
		int tmp = BinaryTreeLevelKSize(root, i);
		if (tmp > max)
		{
			max = tmp;
		}
		i++;
	}
	return max;
}

//二叉树与树的相互转换
//二叉树转换成树
TNode* ExchangeToTree(BTNode* root)
{
	if (root == NULL)
	{
		return NULL;
	}
	else
	{
		TNode* troot = (TNode*)malloc(sizeof(TNode));
		troot->data = root->data;
		troot->leftchild = ExchangeToTree(root->left);
		troot->rightbrother = ExchangeToTree(root->right);
		return troot;
	}
}

//树转换成二叉树
TNode* ExchangeToBinaryTree(TNode* troot)
{
	if (troot == NULL)
	{
		return NULL;
	}
	else
	{
		BTNode* root = (BTNode*)malloc(sizeof(BTNode));
		root->data = troot->data;
		root->left = ExchangeToBinaryTree(troot->leftchild);
		root->right = ExchangeToBinaryTree(troot->rightbrother);

		return root;
	}

}

//打印树
void ShowTree(TNode* troot)
{
	TNode* child = troot->leftchild;
	int flag = 1; //设置标记
	while (flag)
	{
		flag = 0;
		while (troot)
		{
			printf("%d ", troot->data);
			if (troot->leftchild)
			{
				flag = 1;
				child = troot->leftchild; //标记下一层的第一个结点
				//若没有下一层结点，则flag为0，退出循环
			}
			troot = troot->rightbrother;
		}
		printf("\n");
		troot = child;
	}
	printf("\n");
}

//查找二叉排序树中的最小值结点
BTNode* FindMin(BTNode* root) 
{
	if (root == NULL) 
	{
		return NULL;
	}
	else if (root->left == NULL) 
	{
		return root;
	}
	else 
	{
		return FindMin(root->left);
	}
}

// 销毁二叉树，释放空间
void DestroyBTree(BTNode* root) 
{
	if (root == NULL) 
	{
		return;
	}
	DestroyBTree(root->left);
	DestroyBTree(root->right);
	free(root);
}

四.测试

 1.代码

int main()
{
	BTNode* root = NULL;

	//插入结点
	CreateBinaryTree(&root, 9);
	CreateBinaryTree(&root, 5);
	CreateBinaryTree(&root, 7);
	CreateBinaryTree(&root, 8);
	CreateBinaryTree(&root, 6);
	CreateBinaryTree(&root, 4);

	二叉树节点个数
	printf("二叉树的结点个数：%d\n", BinaryTreeSize(root));

	//二叉树的最大宽度
	printf("二叉树的最大宽度:%d\n", BinaryTreeWidthMax(root));

	//二叉树叶子结点的个数
	printf("二叉树叶子结点的个数:%d\n", BinaryTreeLeafSize(root));

	//二叉树第k层节点个数
	printf("二叉树第k层节点个数:%d\n\n", BinaryTreeLevelKSize(root, 3));

	//前、中、后序遍历
	printf("二叉树的前序遍历：");
	PreOrder(root);
	printf("\n中序遍历：");
	InOrder(root);
	printf("\n后序遍历：");
	PostOrder(root);
	printf("\n");
	printf("\n");

	//寻找两个结点的公共祖先
	BTNode* node = PublicAncestors(root, 6, 8);
	printf("5和11两个结点的公共祖先:%d\n ", node->data);

	//二叉排序树关键字5的查找长度
	int lenth = FindBinaryTree(root, 5);
	printf("二叉排序树关键字5的查找长度:%d\n\n ", lenth);

	//删除数据为5的结点
	root = DeleteBTNode(root, 5);
	printf("删除数据为5的结点之后的中序遍历：");
	InOrder(root);
	printf("\n");

	//二叉树转换成树
	TNode* troot = ExchangeToTree(root);
	printf("二叉树转换成树：\n");
	ShowTree(troot);
	printf("\n");

	//树转换成二叉树
	BTNode* tmproot = ExchangeToBinaryTree(troot);
	printf("树转换成二叉树（中序遍历）：\n");
	InOrder(tmproot);
	printf("\n");
	DestroyBTree(tmproot);

	DestroyBTree(root);
	return 0;
}

2.运行结果