题目

给定节点数为 n 的二叉树的前序遍历和中序遍历结果，请重建出该二叉树并返回它的头结点。

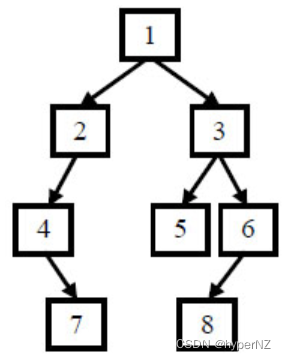
例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建出如下图所示。

提示:

1.vin.length == pre.length

2.pre 和 vin 均无重复元素

3.vin出现的元素均出现在 pre里

4.只需要返回根结点，系统会自动输出整颗树做答案对比

数据范围：n≤2000，节点的值 −10000≤val≤10000

要求：空间复杂度 O(n)，时间复杂度 O(n)

示例1

输入：[1,2,4,7,3,5,6,8],[4,7,2,1,5,3,8,6]

返回值：{1,2,3,4,#,5,6,#,7,#,#,8}

说明：返回根节点，系统会输出整颗二叉树对比结果，重建结果如题面图示

示例2

输入：[1],[1]

返回值：{1}

示例3

输入：[1,2,3,4,5,6,7],[3,2,4,1,6,5,7]

返回值：{1,2,5,3,4,6,7}

---

思路：递归

• 以前序遍历的第一个元素作为根节点root。
• 遍历中序序列，找root位置。
• 根据root将前序序列、中序序列分隔为左子树、右子树的前序序列、中序序列。
• 递归构建左右子树即可。

语法：按区间（左闭右开）复制数组

Arrays.copyOfRange(arr, i, j);

---

代码

import java.util.*;
/**
 * Definition for binary tree
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    public TreeNode reConstructBinaryTree(int [] pre,int [] vin) {
        if(pre.length == 0 || vin.length == 0) {
            return null;
        }
        if(pre.length == 1 && vin.length == 1 && pre[0] == vin[0]) {
            return new TreeNode(pre[0]);
        }

        TreeNode root = new TreeNode(pre[0]);
        int n = pre.length;
        for(int i = 0; i < n; i++) {
            if(vin[i] == pre[0]) {
                root.left = reConstructBinaryTree(Arrays.copyOfRange(pre, 1, i + 1), Arrays.copyOfRange(vin, 0, i));
                root.right = reConstructBinaryTree(Arrays.copyOfRange(pre, i + 1, n), Arrays.copyOfRange(vin, i + 1, n));
                break;
            }
        }
        return root;
    }
}