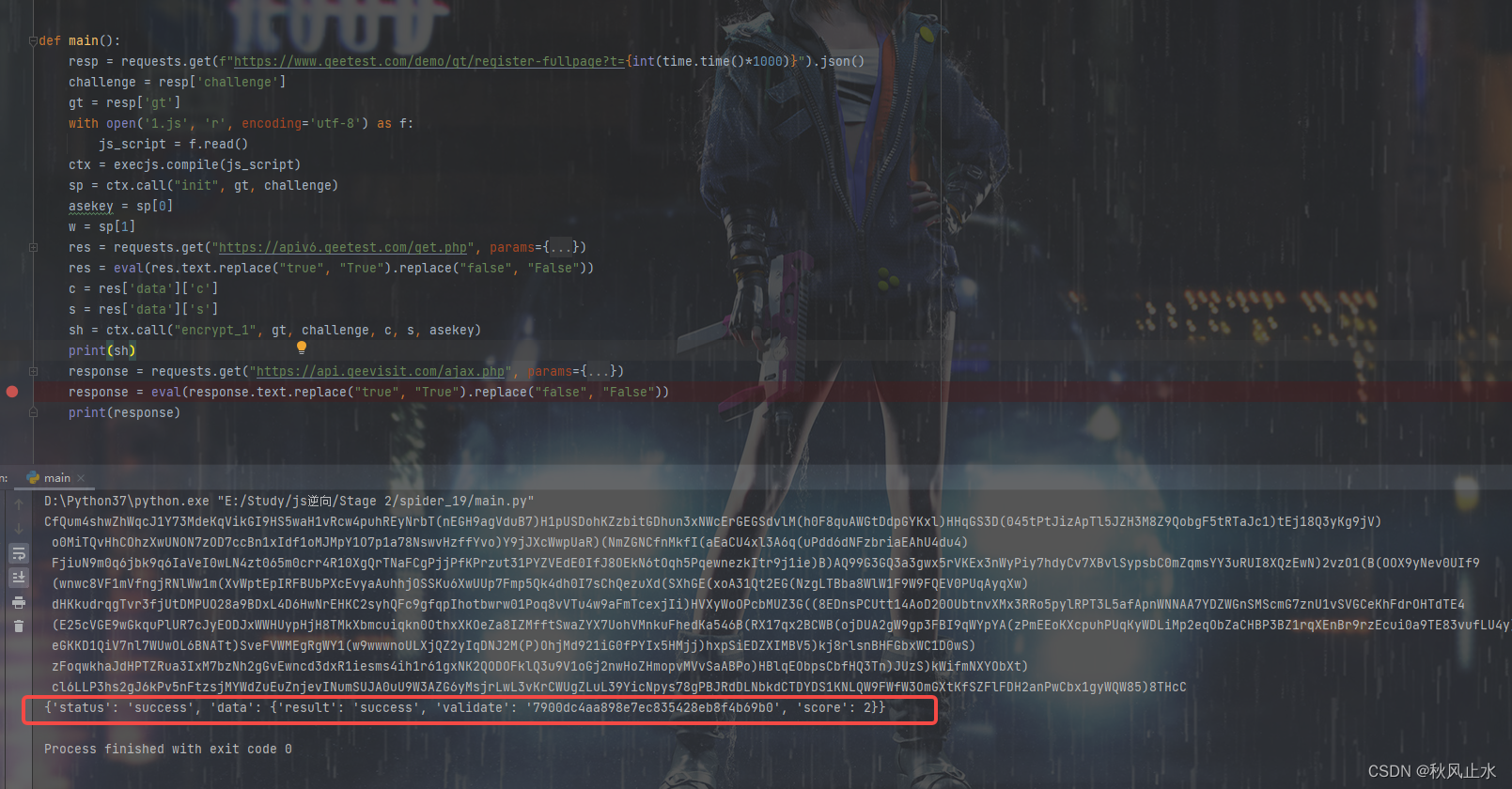
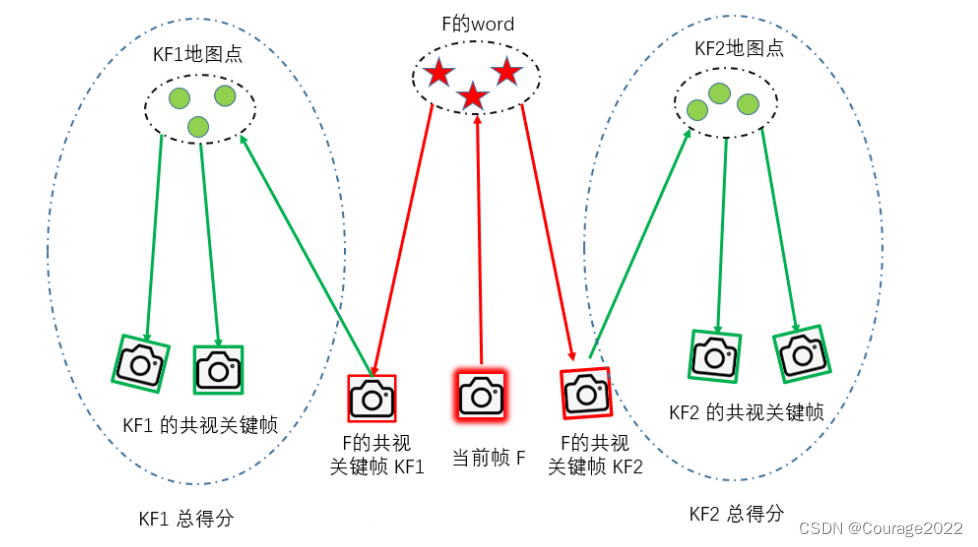
有向图的拓扑序列
给定一个 n n n 个点 m m m 条边的有向图,点的编号是 1 1 1 到 n n n,图中可能存在重边和自环。
请输出任意一个该有向图的拓扑序列,如果拓扑序列不存在,则输出 −1。
若一个由图中所有点构成的序列 A A A 满足:对于图中的每条边 ( x , y ) (x,y) (x,y), x x x 在 A A A 中都出现在 y y y 之前,则称 A A A 是该图的一个拓扑序列。
输入格式
第一行包含两个整数
n
n
n 和
m
m
m。
接下来 m m m 行,每行包含两个整数 x x x 和 y y y,表示存在一条从点 x x x 到点 y y y 的有向边 ( x , y ) (x,y) (x,y)。
输出格式
共一行,如果存在拓扑序列,则输出任意一个合法的拓扑序列即可。
否则输出 −1。
数据范围
1
≤
n
,
m
≤
1
0
5
1≤n,m≤10^5
1≤n,m≤105
输入样例:
3 3
1 2
2 3
1 3
输出样例:
1 2 3
前言
- 只有有向图才可能存在拓扑序列,无向图没这个概念。
- 如果有向图中存在一个环,那必定不可能拓扑序列,因为定义不了起点和终点。
- 拓扑序列如果有,可能不唯一。
具体分析
这里偷个懒吧hh,图片、简介引用一下该博主的文章:拓扑排序−−思路介绍+图解模拟+详细代码注释。
再说说自己的理解:
其中,提到了一个删边的思路,那么为什么可以这么做又为什么是对的呢?
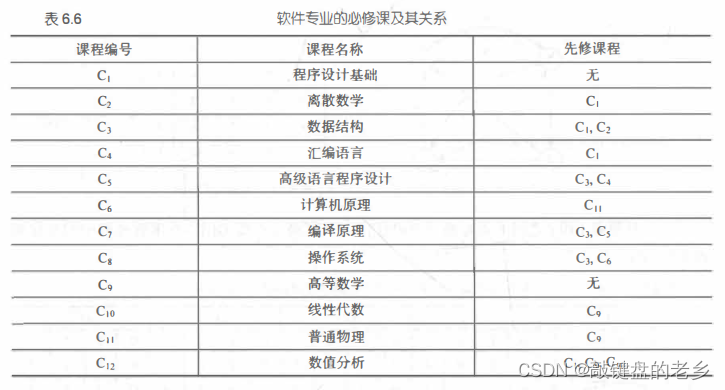
其实可以这么理解,不知道大家在学习《数据结构》的这一章时是否看到过一个用 “拓扑排序安排课程顺序” 的例子(如下图所示),大概之意就是有些课会存在先修课,然后先修课也可能还会有先修课… …,必须要学了先修课后才能往后学,然后给出一个课程学习顺序可以合理地学完所有课程,其实就是上面题意给具象化了一下。那么“删边”在这个例子里面意味着什么呢?其实就意味着 “该门课的一门先选课已经学了,不用再考虑它们之间的关系了”。如果所有课的先修课都能被忽略掉就说明所有课学完了,正好对应上了要求。
所以将那些没有入度(先修课)的点作为拓扑序的起点,将它们先存到队列里,然后往后挨着取队头并对连接在它后面的那些点做删边操作,如果此时碰到了后面的某个点的入度 = 0,说明它也可以做为新的起点,将其也入到队列里边。
最后如果所有点都入过一遍队列里即队列的大小为 n n n的话,说明整个图就存在一个拓扑序列,具体的序列就是入队的顺序。否则就是不存在拓扑序列。
这里的队列用到的是模拟队列,好处是对于点的出队并不会真正地将其删除,而是移动指针,那么最后想要输出入队顺序其实也就是从0到队尾tt枚举输出q[]数组的元素值。
Code
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
const int N = 1e5 + 10;
int q[N], hh = 0, tt = -1; //模拟队列
int n, m;
int e[N], ne[N], h[N], d[N], idx = 0; //d[]是存入度的
void add(int a, int b){ //邻接表
e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}
bool top_sort(){
for(int i = 1;i <= n;i ++)
if(d[i] == 0)
q[++ tt] = i; //把入度为0的点作为起点入队
while(hh <= tt){
int t = q[hh ++];
for(int i = h[t]; ~i ;i = ne[i]){ //用其扩展
int j = e[i];
d[j] --;
if(d[j] == 0) //作为新的一个起点
q[++ tt] = j;
}
}
return tt == n - 1; //说明此时的所有点都可以入队
}
int main(){
memset(h, -1, sizeof h);
cin >> n >> m;
ios :: sync_with_stdio(false);
while(m --){
int u, v;
cin >> u >> v;
add(u, v);
d[v] ++;
}
if(top_sort()){
for(int i = 0;i <= tt;i ++)
cout << q[i] << " ";
}
else{
cout << -1 << endl;
}
return 0;
}